差分法公式推导xin

第三章 有限差分法函数()f x ，x 为定义在区间[]a b ,上的连续变 量。

将区间[]a b ,等分成n 份，令()h b a n =-称为 步长，x 在这些离散点处的取值为x a ih i =+ ()i n =01,,,称为节点。

函数()f x 在这些节点处的差值()()()()()()f x h f x f x f x h f x h f x h i i i i i i +---+--⎧⎨⎪⎩⎪(5-1)分别称为一阶向前、向后和中心差分，可以用它 们作为函数()f x 在x i 处的微分近似值。

这些差分 与相应x 区间的比值()()[]()()[]()()[]1112h f x h f x h f x f x h h f x h f x h i i i i i i +---+--⎧⎨⎪⎪⎪⎩⎪⎪⎪ (5-2) 分别称为一阶向前、向后和中心差商，可以用它 们作为函数()f x 在x i 处的导数近似值。

完全类似地可以定义高阶差商，例如常用的二阶中心差商()()()[]122hf x h f x f x h i i i +-+- (5-3)可以作为函数()f x 在x i 处的二阶导数近似值。

§3.1 常微分方程初值问题的差分解法考虑电学中的一个问题：如图5-1。

研究 电容器上的电荷随时间的变化规律。

图5-1 RC 放电回路这个问题对应的微分方程及其定解条件为：d d Q tQ RC QQ t =-=⎧⎨⎪⎩⎪=00(5-4) 这是一阶微分方程的初值问题，它的解析解为 Q Q e t RC =-0 (5-5)一、欧拉(Euler )折线法求解下列普遍形式的一阶微分方程的初值 问题：()[]()'=∈=⎧⎨⎪⎩⎪y f x y x a b y a y ,,0(5-6) 首先，将区间[]a b ,等分n 份，取值a x x xb n =<<<=01 ，步长h x x i i =-+1。

★【速算技巧五：差分法】李委明提示：“差分法”是在比较两个分数大小时，用“直除法”或者“化同法”等其他速算方式难以解决时可以采取的一种速算方式。

适用形式：两个分数作比较时，若其中一个分数的分子与分母都比另外一个分数的分子与分母分别仅仅大一点，这时候使用“直除法”、“化同法”经常很难比较出大小关系，而使用“差分法”却可以很好地解决这样的问题。

基础定义：在满足“适用形式”的两个分数中，我们定义分子与分母都比较大的分数叫“大分数”，分子与分母都比较小的分数叫“小分数”，而这两个分数的分子、分母分别做差得到的新的分数我们定义为“差分数”。

例如：324/53.1与313/51.7比较大小，其中324/53.1就是“大分数”，313/51.7就是“小分数”，而324-313/53.1-51.7=11/1.4就是“差分数”。

“差分法”使用基本准则——“差分数．．．：．．．”作比较．．．”代替．．．”与．“小分数．．“大分数1、若差分数比小分数大，则大分数比小分数大；2、若差分数比小分数小，则大分数比小分数小；3、若差分数与小分数相等，则大分数与小分数相等。

比如上文中就是“11/1.4代替324/53.1与313/51.7作比较”，因为11/1.4＞313/51.7（可以通过“直除法”或者“化同法”简单得到），所以324/53.1＞313/51.7。

特别注意：一、“差分法”本身是一种“精算法”而非“估算法”，得出来的大小关系是精确的关系而非粗略的关系；二、“差分法”与“化同法”经常联系在一起使用，“化同法紧接差分法”与“差分法紧接化同法”是资料分析速算当中经常遇到的两种情形。

三、“差分法”得到“差分数”与“小分数”做比较的时候，还经常需要用到“直除法”。

四、如果两个分数相隔非常近，我们甚至需要反复运用两次“差分法”，这种情况相对比较复杂，但如果运用熟练，同样可以大幅度简化计算。

【例1】比较7/4和9/5的大小【解析】运用“差分法”来比较这两个分数的大小关系：大分数小分数9/5 7/49－7/5－1=2/1(差分数)根据：差分数=2/1＞7/4=小分数因此：大分数=9/5＞7/4=小分数李委明提示：使用“差分法”的时候，牢记将“差分数”写在“大分数”的一侧，因为它代替的是“大分数”，然后再跟“小分数”做比较。

差分法：通过数列的差分性质，求得通项。

差分法：通过数列的差分性质，求得通项简介差分法是一种通过数列的差分性质来推导数列通项的方法。

差分法可以应用于各种数列，包括等差数列和等比数列。

通过观察数列的差分，我们可以找到数列的规律，并推导出数列的通项公式。

差分法的步骤1. 确定数列的差分次数：根据所给数列的性质，确定需要进行几次差分才能找到规律；2. 进行差分运算：将数列的连续项之间进行差分运算，得出新的数列；3. 分析差分后的数列：观察新数列的性质，判断是否存在某种规律；4. 推导数列通项公式：利用差分后的数列的性质，得出数列的通项公式。

例子假设有一个等差数列：1, 3, 5, 7, 9，我们想通过差分法求得该数列的通项。

1. 确定差分次数：由于该数列的项之间的差值都为2，我们只需要进行一次差分运算即可。

2. 进行差分运算：对该数列进行一次差分运算，得到新的数列：2, 2, 2, 2。

3. 分析差分后的数列：观察新数列，发现所有项的值都相同，说明这是一个等差数列。

4. 推导通项公式：由于每次差分的结果都是2，我们可以得出差分前的项之间的关系为+2，即 a(n) = a(n-1) + 2。

通过差分法，我们成功地推导出了等差数列 1, 3, 5, 7, 9 的通项公式：a(n) = 2n - 1。

总结差分法是一种简单而有效的方法，通过数列的差分性质可以推导出数列的通项公式。

通过确定差分次数、进行差分运算、分析差分后的数列和推导通项公式，我们可以解决各种数列问题，并找到数列的规律。

差分法在数学中有广泛的应用，对于求解数列问题很有帮助。

差分法的原理一、差分法的概述差分法是一种常用的数值计算方法，它通过对函数的差分进行近似求解，从而得到函数在某些点上的近似值。

差分法可以用于求解各种类型的微分方程和积分方程，也可以用于对数据进行平滑处理和趋势预测等。

二、差分法的基本原理差分法的基本原理是利用函数在某个点附近的导数与函数在该点处的取值之间的关系来进行近似计算。

具体来说，如果我们想要求解函数f(x)在x=x0处的导数f'(x0)，我们可以通过计算函数在x0+h和x0-h 两个点上取值之间的差异来近似求解。

这个过程可以表示为：f'(x0) ≈ [f(x0+h) - f(x0-h)] / (2h)其中h为一个足够小的正数，它表示我们所使用的差分步长。

当h越小时，我们得到的结果就会越接近于真实值。

三、一阶前向差分法一阶前向差分法是最简单、最基础也是最常用的一种差分方法。

它通过计算函数在相邻两个点上取值之间的差异来进行近似求解。

具体来说，如果我们想要求解函数f(x)在x=x0处的导数f'(x0)，我们可以通过计算函数在x=x0和x=x0+h两个点上取值之间的差异来近似求解。

这个过程可以表示为：f'(x0) ≈ [f(x0+h) - f(x0)] / h其中h为一个足够小的正数，它表示我们所使用的差分步长。

当h越小时，我们得到的结果就会越接近于真实值。

四、一阶后向差分法一阶后向差分法也是一种常用的差分方法。

它与一阶前向差分法相似，只是计算函数在相邻两个点上取值之间的差异时采用了不同的方式。

具体来说，如果我们想要求解函数f(x)在x=x0处的导数f'(x0)，我们可以通过计算函数在x=x0-h和x=x0两个点上取值之间的差异来近似求解。

这个过程可以表示为：f'(x0) ≈ [f(x0) - f(x0-h)] / h其中h为一个足够小的正数，它表示我们所使用的差分步长。

当h越小时，我们得到的结果就会越接近于真实值。

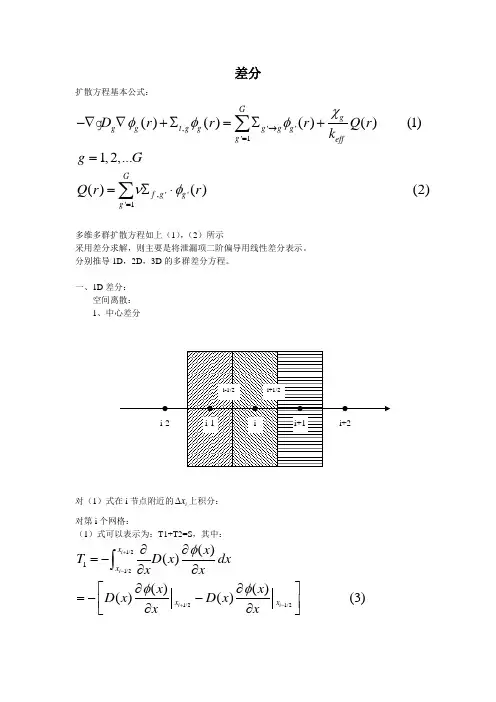
差分扩散方程基本公式：,'''1,'''1()()()()(1)1,2,...()()(2)Ggg g t g g g g g g effGf g g g D r r r Q r k g GQ r r χφφφνφ→==-∇∇+∑=∑+==∑⋅∑∑多维多群扩散方程如上（1），（2）所示采用差分求解，则主要是将泄漏项二阶偏导用线性差分表示。

分别推导1D ，2D ，3D 的多群差分方程。

一、1D 差分： 空间离散： 1、中心差分对（1）式在i 节点附近的i x ∆上积分： 对第i 个网格：（1）式可以表示为：T1+T2=S ，其中：1/21/21/21/21()()()()()()(3)i i i i x x x x x T D x dxx x x x D x D x x x φφφ+-+-∂∂=-∂∂∂∂⎡⎤=--⎢⎥∂∂⎣⎦⎰由差分法可得：1/21/211/21/2111/21/2111()()(4)22()()(5)1122i i i i i ix i ii i i i i i x i i i i x D x D D x x x x D x D D xx x φφφφφφφφφφ+-+++++-------∂==∂∆∆--∂==∂∆∆由（4）、（5）可得：11/21/211111/211/21111/211/2111/211/2111111/21122()()i i i ii ii i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i D D x x D x D x D x D x D x D x D x D x D x D x D x D φφφφφφφφφφφφφφφφφφ+++++++++++++++++++++++++++--=∆∆⇒∆-=∆-⇒∆-∆=∆-∆⇒∆+∆=∆+∆∆+⇒=111111111/21/2111111111111111111111222()2()2i i i i i i ii i i i i ii i i i i i i i ii i i i i i i i i i i i i i i i ii i i i i i i i i x D x D x D x D x D x D x D D D x x x D x D x D x D x D x D x D x D D φφφφφφφφφφφφ++++++++++++++++++++++++++++∆∆+∆∆+∆---∆+∆∴==∆∆∆∆+∆-∆-∆=∆∆+∆∆=1111111111111111111111*111111()2()22()6()i i i i i i i i i ii i i i i i i i i i ii i i i i i i ii i i i i i i i i ii i i i i i i i ix D x D x D x x D x D x D x D x D x D x D x D D x D D D x D x D φφφφφφφφφφφ+++++++++++++++++++++++++++++∆-∆-∆∆∆+∆∆-∆=∆∆+∆-=∆-==-∆+∆（*11112i i i i i i iD D DD x D x ++++=∆+∆）其中，同理，1/21/2111*11111*11111222()7()2i i i i ii i i i i ii i i i i i i i i iii i i i D D x x D D D x D x D D D D D x D x φφφφφφφφ---------------∴==∆∆-==-∆+∆=∆+∆（）其中，所以，**1111****1111****1111T [()()]()(8)i i i i i i i i i i i i i i i i i i i i i D D D D D D D D D D φφφφφφφφφφφ++-+++-+++-=----=-++-=-++-2,T (9)t i i ix φ=∑∆则差分方程为：：****11,11()(10)i i i i t i i i i i iD D D x D S φφφ-+++-+++∑∆-=可表示成如下形式：1112222233333411111111121111(11)left i i i i i i i ii i i i i i i n n n n n right n n nn s b a s a b a s a b a s a b a s a b a s a b a s a b a s a b φφφφφφφφ----++++++----⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭*,1*11i i i t i i i i i i a D b x a a a D +++=-=∑∆--=-边界条件： a.左边界：（1）零通量边界条件：0.0sφ=对于左边界第一个节块，其左边中子流可以写为：111()()(12)12sleftx D x D xx φφφ-∂=∂∆右边中子流表达方式不变。