弯矩作用下热塑性复合材料悬臂梁弹塑性分析

悬臂梁在循环加载作用下的弹塑性计算摘要：本文介绍了悬臂梁在循环荷载作用下基于Ansys有限元软件进行弹塑性分析的过程，分析了材料为多线性弹性材料的悬臂梁在循环荷载作用下观测点P的水平方向的应力应变历程，并给出了相应的结果。

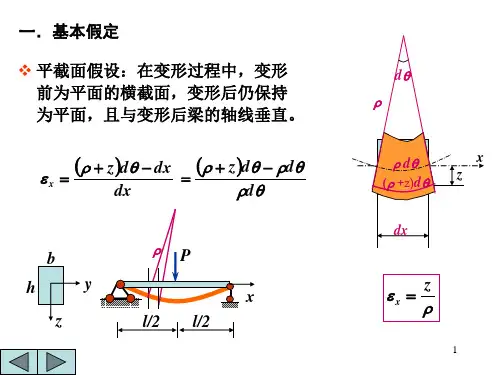
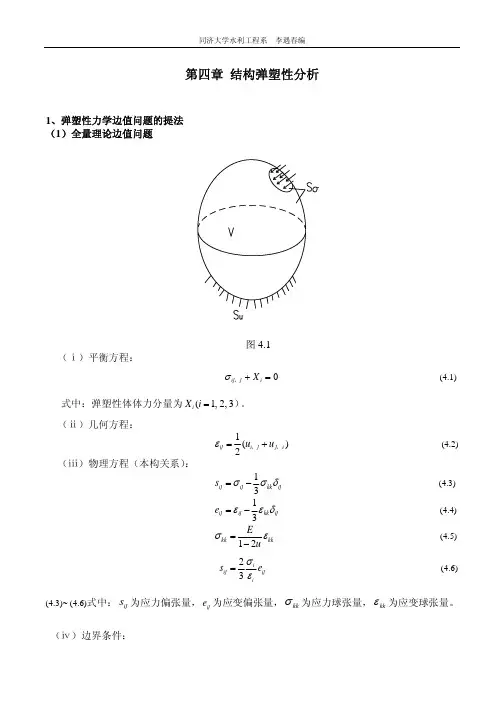
关键词：有限元，弹塑性，悬臂梁，应力应变Elastoplastic Calculation of Cantilever Beam UnderCyclic LoadingAbstract:This article describes the process of a cantilever beam under cyclic loading Ansys finite element software elastoplastic analysis, and analyzes history of the horizontal direction of the observation point P of the cantilever whose material is multi-linear elastic material under cyclic loading stress strain. And gives the corresponding results.Key words: finite element,elastoplastic, cantilever, stress-strain.1.前言一个左端固定的悬臂梁见图 1-1(a)，厚度为 1cm,在它的右段中点上施加有一个集中力，该集中力为循环载荷见图 1-1(b)，悬臂梁的材料为多线性弹性材料，材料的弹性模量为 20000 N/cm2，实验获得的该材料的非线性应力-应变行为见表1-1，分析该悬臂梁在循环载荷作用下的观测点 P 的水平方向上的应力应变历程。

图1-1 一个悬臂梁示意图以及加载历程图表1-1 材料的应力-应变行为实验数据为考察悬臂梁根部P点的应力-应变历程，采用2D的计算模型，使用平面单元PLANE42，材料采用多线性弹塑性模型(mkin)，进行循环加载过程的分析。

潜在类别分析原理及实例分析潜在类别分析是一种广泛应用于诸多领域的数据分析方法，它通过探究数据中隐藏的类别结构，帮助研究者更好地理解和解释数据。

在本文中，我们将深入探讨潜在类别分析的原理，并通过实际例子来展示其应用和重要性。

潜在类别分析是一种基于概率模型的数据分析方法，它通过建立一系列的概率统计模型来揭示数据中隐藏的类别结构。

该方法将数据中的观察值视为随机样本，每个观察值所属的类别由其特征决定的概率分布决定。

潜在类别分析利用统计推理和最大似然估计等手段，估计出各个类别的概率分布和似然函数，从而将数据中的观察值划分为不同的潜在类别。

以一个电商平台的数据为例，我们可以通过潜在类别分析来探究消费者购物行为的异同。

假设我们有两个特征：消费者的购物频率和购物金额。

我们希望通过这两个特征将消费者划分为不同的类别。

我们可以运用因子分析或聚类分析等方法对数据进行探索性分析，以了解数据的潜在结构。

然后，我们可以通过潜在类别分析建立概率模型，并使用迭代方法来估计模型参数并进行类别划分。

通过潜在类别分析，我们可能会发现两个潜在类别：一类是高频低值消费者，他们经常购物但每次购物的金额相对较低；另一类是低频高值消费者，他们购物的频率较低，但每次购物的金额较高。

这两个类别反映了消费者不同的购物行为和消费习惯。

数据收集和预处理：收集包含多个特征的数据，并进行数据清洗、缺失值处理等预处理工作。

探索性分析：通过因子分析、聚类分析等手段了解数据的潜在结构，为后续的潜在类别分析提供参考。

模型选择与参数估计：选择合适的概率模型（如高斯混合模型、朴素贝叶斯分类器等），并利用迭代方法估计模型参数，这包括各个类别的概率分布和似然函数。

类别划分：根据估计的模型参数，将数据中的观察值划分为不同的潜在类别。

结果解释与分析：对划分的类别进行解释和分析，探究不同类别之间的异同以及类别的优缺点。

在上述电商平台的例子中，我们通过潜在类别分析将消费者划分为高频低值和低频高值两个类别。

例一：悬臂梁在循环加载作用下的弹塑性计算(GUI)一、问题描述：一个左端固定的悬臂梁见图1-1(a)，厚度为1cm,在它的右段中点上施加有一个集中力，该集中力为循环载荷见图1-1(b)，悬臂梁的材料为多线性弹性材料，材料的弹性模量为20000，实验获得的该材料的非线性应力-应变行为见表1-2，分析该悬臂梁在循环载荷作用下的观测点P的水平方向上的应力应变历程。

(a)悬臂梁以及加载位置(cm)(b)所受的循环载荷(N)图1-1一个悬臂梁以及加载历程表1-2 〉材料的应力-应变行为实验数据二、问题分析解答：为考察悬臂梁根部P点的应力-应变历程，采用2D的计算模型，使用平面单元PLANE42，材料采用多线性弹塑性模型(mkin)，进行循环加载过程的分析。

建模的要点如下：①设置几何以及材料参数，②输入材料的多线性弹塑性模型(包括：弹性模量、屈服极限)，见图1-3；③通过设置time来给出加载历程，每次加载都输入当时的状态载荷值，不是增量加载，每次加载后，必须进行计算，再进入下一步的计算；④在时间后处理中，通过设置几何位置来查询对应的P观测点的节点编号，并设置观测点的应力显示变量(2号变量)以及塑性应变为显示变量(3号变量)，最后将3号变量设置为横轴，画出2号变量随3号变量的变化曲线见图1-4，可以看出，该材料具有非常明显的Bauschinger效应(即正向屈服与反向屈服之和是单拉实验屈服极限的2倍)。

给出的基于图形界面(GUI)的交互式操作(step by step)过程如下：(1) 进入ANSYS（设定工作目录和工作文件）程序→ANSYS →ANSYS Interactive →Working directory（设置工作目录）→Initial jobname（设置工作文件名）: Beams →Run →OK(2) 设置计算类型ANSYS Main Menu：Preferences… →Structural →OK(3) 设定不显示时间ANSYS Utility Menu：PlotCtrls→Window Controls →Window Options… →DATE：No Date or Time →OK(4) 定义单元类型ANSYS Main Menu：Preprocessor →Element Type →Add/Edit/Delete... →Add…→Solid: Quad 4node 42 →OK（返回到Element Types窗口）→Close(5) 定义材料参数ANSYS Main Menu: Preprocessor →Material Props →Material Models →Structural →Linear →Elastic →Isotropic →输入EX: 2E4, PRXY: 0.3 (定义弹性模量及泊松比) →OK →返回Define Material ModelBehavior 窗口Structural →NonLinear→Inelastic →Rate Independent →Kinematic Hardening Plasticity →Mises Plasticity →Multilinear (Fixed table) →在Strain一行中对应1至4号点输入0.004、0.015、0.03、0.08 →在Curve1中对应1至4号点输入80、160、210、280 →点击右下角Graph→OK →Close（关闭材料定义窗口），见图1-3，观察窗口中的多线性弹塑性模型(6) 构造模型生成关键点ANSYS Main Menu：Preprocessor →Modeling →Create →Keypoints→In Active CS →Keypoints number：1，X，Y，Z Location in active CS：0，0，0 →Apply →同样依次输入其他三个关键点（100，0，0）、（100，10，0）与（0，10，0）→OKANSYS Main Menu：Preprocessor →Modeling →Create →Areas →Arbitrary →Through KPs →用鼠标依次点击1、2、3、4关键点，生成面单元，见图1-5构造模型图(7) 网格划分ANSYS Main Menu：Preprocessor →Meshing →Mesher Opts →Mesher Type : Mapped →OK →2D Shape Key : Quad →OKANSYS Main Menu：Preprocessor →Meshing →size contrls→ManualSize→Lines →Picked Lines →选择上下两条横边线，Ok →NDIV 设置为20 →Apply →选择两条竖边线→Ok →NDIV设置为8 →OK ANSYS Main Menu：Preprocessor →Meshing →Mesh →Areas →Target Surf →点击生成面几何体的位置，显示矩形面被选中→OK，见图1-6网格划分图(8) 模型加约束ANSYS Main Menu: Solution →Define Loads →Apply →Structural →Displacement On Lines →选取左侧边线（L4）→OK →select Lab2: All DOF(施加全部约束) →OK，见图1-7模型加约束图(9)求解设置ANSYS Main Menu : Solution →Analysis Type →Sol’n Controls →在Basic标签下设置Analysis Options 为Large Displacement Satic，Number of substeps: 8, Max no. of substeps :25Min no. Of substeps:2, Frequency 设置为Write N number of substeps Where N = 10 →OK(10)按照时间步施加循环载荷ANSYS Main Menu : Solution →Analysis Type →Sol’n Controls →在Basic标签下设置Time at end of loadstep:1 →OKANSYS Main Menu : Solution →Define Loads →Apply →Structural →Force/Moment →On Nodes →选择右侧边缘中点（26号节点）→OK →Lab：Fy，Value：-40 →OK，结果见图1-8ANSYS Main Menu：Solution →Solve →Current LS →OK，结果见图1-9ANSYS Utility Menu : Plot →ReplotANSYS Main Menu : Solution →Analysis Type →Sol’n Controls →在Basic标签下设置Time at end of loadstep: 2 →OKANSYS Main Menu : Solution →Define Loads →Apply →Structural →Force/Moment →On Nodes →选择右侧边缘中点（26号节点）→OK→Lab：Fy，Value：0 →OK，结果见图1-10ANSYS Main Menu：Solution →Solve →Current LS →OK，ANSYS Utility Menu : Plot →ReplotANSYS Main Menu : Solution →Analysis Type →Sol’n Controls →在Basic标签下设置Time at end of loadstep: 3 →OKANSYS Main Menu : Solution →Define Loads →Apply →Structural →Force/Moment →On Nodes →选择右侧边缘中点（26号节点）→OK →Lab：Fy，Value：40 →OK，结果见图1-11ANSYS Main Menu：Solution →Solve →Current LS →OK，结果见图1-12ANSYS Utility Menu : Plot →ReplotANSYS Main Menu : Solution →Analysis Type →Sol’n Controls →在Basic标签下设置Time at end of loadstep: 4 →OKANSYS Main Menu : Solution →Define Loads →Apply →Structural →Force/Moment →On Nodes →选择右侧边缘中点（26号节点）→Lab：Fy，Value：0 →OK，结果见图1-13ANSYS Main Menu：Solution →Solve →Current LS →OK，结果见图1-14ANSYS Utility Menu : Plot →ReplotANSYS Main Menu : Solution →Analysis Type →Sol’n Controls →在Basic标签下设置Time at end of loadstep: 5 →OKANSYS Main Menu : Solution →Define Loads →Apply →Structural →Force/Moment →On Nodes →选择右侧边缘中点（26号节点）→Lab：Fy，Value：-40 →OK，结果见图1-15ANSYS Main Menu：Solution →Solve →Current LS →OK，结果见图1-16ANSYS Utility Menu : Plot →ReplotANSYS Main Menu : Solution →Analysis Type →Sol’n Controls →在Basic标签下设置Time at end of loadstep: 6 →OKANSYS Main Menu : Solution →Define Loads →Apply →Structural →Force/Moment →On Nodes →选择右侧边缘中点（26号节点）→Lab：Fy，Value：0 →OK，结果见图1-17ANSYS Main Menu：Solution →Solve →Current LS →OK，结果见图1-18(11) 计算结果ANSYS Main Menu：General Postproc→Read Results →Last SetANSYS Main Menu：General Postproc→Plot Results →Deformed Shape →Def + Undeformed→OK，观察最后变形情况，见图1-19ANSYS Main Menu：General Postproc→Plot Results →Contour Plot →Element solu→PlasticStrain →Equivalent plastic strain →OK，观察累计的等效塑性应变，见图1-20ANSYS Main Menu：TimeHistPostpro→关闭弹出窗口→Define Variables →Add… →Element Results →OK 在方框中输入2 →OK 在方框中输入4 →OK →在Item，Comp Data item 中选择Stress, X-direction SX →OK返回Define Time-History Variables →Add… →Element Results →OK 在方框中输入2 →OK 在方框中输入4 →OK →在Item，Comp Data item 中选择Strain-plastic, X-dir’n EPPL X →OK →Close ANSYS Main Menu：TimeHistPostpro→关闭弹出窗口→Settings →Graph →Single Variable No. 输入3 →OKANSYS Main Menu：TimeHistPostpro→关闭弹出窗口→Graph Variables →Nvar1中输入2 →OK观察观测点P上的应力应变历程(SX)，见图1-4ANSYS Utility Menu：File →Exit →Save Everything →OK三、ANSYS分析结果：图1-3 多线性弹塑性模型图1-4 观测点P上的应力应变历程(SX)图1-5 构造模型图图1-6 网格划分图图1-7 模型加约束图图1-8图1-9 图1-10图1-11 图1-12图1-13 图1-14图1-15 图1-16图1-17图1-18图1-19 图1-20。

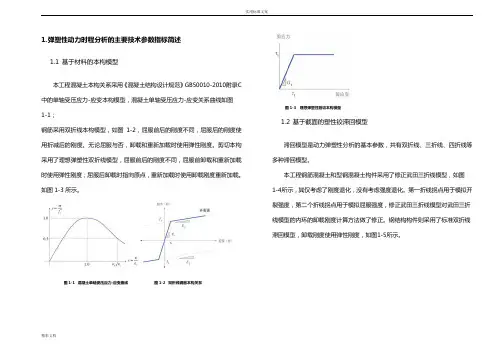
1.弹塑性动力时程分析的主要技术参数指标简述1.1基于材料的本构模型本工程混凝土本构关系采用《混凝土结构设计规范》GB50010-2010附录C 中的单轴受压应力-应变本构模型，混凝土单轴受压应力-应变关系曲线如图1-1；钢筋采用双折线本构模型，如图1-2，屈服前后的刚度不同，屈服后的刚度使用折减后的刚度。

无论屈服与否，卸载和重新加载时使用弹性刚度。

剪切本构采用了理想弹塑性双折线模型，屈服前后的刚度不同，屈服前卸载和重新加载时使用弹性刚度；屈服后卸载时指向原点，重新加载时使用卸载刚度重新加载。

如图1-3所示。

图1-1 混凝土单轴受压应力-应变曲线图1-2 双折线钢筋本构关系图1-3 理想弹塑性剪切本构模型1.2基于截面的塑性铰滞回模型滞回模型是动力弹塑性分析的基本参数，共有双折线、三折线、四折线等多种滞回模型。

本工程钢筋混凝土和型钢混凝土构件采用了修正武田三折线模型，如图1-4所示，其仅考虑了刚度退化，没有考虑强度退化。

第一折线拐点用于模拟开裂强度，第二个折线拐点用于模拟屈服强度，修正武田三折线模型对武田三折线模型的内环的卸载刚度计算方法做了修正。

钢结构构件则采用了标准双折线滞回模型，卸载刚度使用弹性刚度，如图1-5所示。

图1-4 修正武田三折线滞回模型图1-5 标准双折线滞回模型1.3非线性梁柱单元程序采用了具有非线性铰特性的梁柱单元。

梁单元公式使用了柔度法（flexibility method），在荷载作用下的变形和位移使用了小变形和平截面假定理论（欧拉贝努利梁理论，Euler Bernoulli Beam Theory），并假设扭矩和轴力、弯矩成分互相独立无关联。

非线性梁柱单元可考虑了P-Δ效应，在分析的每个步骤都会考虑内力对几何刚度的影响重新更新几何刚度矩阵，并将几何刚度矩阵加到结构刚度矩阵中。

根据定义弯矩非线性特性关系的方法，非线性梁柱单元可分为弯矩-旋转角单元（集中铰模型）和弯矩-曲率单元（分布铰模型）。

ＪｏｕｒｎａｌｏｆＭｅｃｈａｎｉｃａｌＳｔｒｅｎｇｔｈ２０２１ꎬ４３(５):１１６２￣１１６９ＤＯＩ:１０ １６５７９/ｊ.ｉｓｓｎ.１００１ ９６６９.２０２１.０５.０２０∗２０２０１２０３收到初稿ꎬ２０２１０３０８收到修改稿ꎮ国家自然科学基金项目(１１９０２３４８)ꎬ湖南省自然科学基金项目(２０２０ＪＪ５６５０)ꎬ国防科技大学科研计划资助项目(ＺＫ２０￣２７)资助ꎮ∗∗刘明伟ꎬ１９９５年生ꎬ黑龙江省伊春市人ꎬ汉族ꎬ国防科技大学硕士研究生ꎬ研究方向为结构分析与设计ꎮ∗∗∗雷勇军(通信作者)ꎬ１９６８年生ꎬ男ꎬ湖南省澧县人ꎬ汉族ꎬ国防科技大学教授ꎬ博士ꎬ博士生导师ꎬ研究方向为计算固体力学ꎮ弯矩作用下热塑性复合材料平面曲梁弹塑性特性分析∗ＥＬＡＳＴＩＣ￣ＰＬＡＳＴＩＣＡＮＡＬＹＳＩＳＦＯＲＴＨＥＲＭＯＰＬＡＳＴＩＣＣＯＭＰＯＳＩＴＥＰＬＡＮＥＣＵＲＶＥＤＢＥＡＭＳＢＹＢＥＮＤＩＮＧＭＯＭＥＮＴ刘明伟∗∗１ꎬ２㊀高艺航１ꎬ２ꎬ３㊀张大鹏１ꎬ２㊀王志祥１ꎬ２㊀雷勇军∗∗∗１ꎬ２(１.国防科技大学空天科学学院ꎬ长沙４１００７３)(２.空天任务智能规划与仿真湖南省重点实验室ꎬ长沙４１００７３)(３.北京宇航系统工程研究所ꎬ北京１０００７６)ＬＩＵＭｉｎｇＷｅｉ１ꎬ２㊀ＧＡＯＹｉＨａｎｇ１ꎬ２ꎬ３㊀ＺＨＡＮＧＤａＰｅｎｇ１ꎬ２㊀ＷＡＮＧＺｈｉＸｉａｎｇ１ꎬ２㊀ＬＥＩＹｏｎｇＪｕｎ１ꎬ２(１.ＣｏｌｌｅｇｅｏｆＡｅｒｏｓｐａｃｅＳｃｉｅｎｃｅꎬＮａｔｉｏｎａｌＵｎｉｖｅｒｓｉｔｙｏｆＤｅｆｅｎｓｅＴｅｃｈｎｏｌｏｇｙꎬＣｈａｎｇｓｈａ４１００７３ꎬＣｈｉｎａ)(２.ＨｕｎａｎＫｅｙＬａｂｏｒａｔｏｒｙｏｆＩｎｔｅｌｌｉｇｅｎｔＰｌａｎｎｉｎｇａｎｄＳｉｍｕｌａｔｉｏｎｆｏｒＡｅｒｏｓｐａｃｅＭｉｓｓｉｏｎｓꎬＣｈａｎｇｓｈａ４１００７３ꎬＣｈｉｎａ)(３.ＢｅｉｊｉｎｇＩｎｓｔｉｔｕｔｅｏｆＡｅｒｏｓｐａｃｅＳｙｓｔｅｍｓＥｎｇｉｎｅｅｒｉｎｇꎬＢｅｉｊｉｎｇ１０００７６ꎬＣｈｉｎａ)摘要㊀热塑性复合材料综合力学性能优异ꎬ具有广阔的应用前景ꎮ针对弯矩作用下热塑性复合材料平面曲梁进行了静力学建模及弹塑性特性分析ꎮ根据极坐标系下平面应力问题的基本方程ꎬ基于单参数塑性模型㊁相关塑性流动准则以及线性应变强化规律ꎬ建立了曲梁的控制方程ꎬ得到了曲梁应力和位移的解析解ꎮ在此基础上ꎬ系统分析了曲梁几何尺寸对截面应力分布的影响ꎬ并结合Ｈａｓｈｉｎ失效准则对曲梁失效形式进行判断ꎮ结果表明ꎬ所建模型在研究热塑性复合材料平面纯弯曲梁弹塑性特性问题中准确有效ꎬ曲梁失效形式与径厚比密切相关ꎮ关键词㊀热塑性复合材料㊀平面曲梁㊀弹塑性㊀单参数塑性模型㊀Ｈａｓｈｉｎ失效准则㊀径厚比中图分类号㊀Ｏ３４４ ３Ａｂｓｔｒａｃｔ㊀Ｔｈｅｒｍｏｐｌａｓｔｉｃｃｏｍｐｏｓｉｔｅｓｈａｖｅｅｘｃｅｌｌｅｎｔｃｏｍｐｒｅｈｅｎｓｉｖｅｍｅｃｈａｎｉｃａｌｐｒｏｐｅｒｔｉｅｓａｎｄｗｉｄｅｌｙａｐｐｌｉｅｄｐｒｏｓｐｅｃｔｓ.Ａｓｔａｔｉｃｍｏｄｅｌｗａｓｅｓｔａｂｌｉｓｈｅｄａｎｄｅｌａｓｔｉｃ￣ｐｌａｓｔｉｃｃｈａｒａｃｔｅｒｉｓｔｉｃｓｗｅｒｅａｎａｌｙｚｅｄｆｏｒａｐｌａｎｅｃｕｒｖｅｄｂｅａｍꎬｗｈｉｃｈｗａｓｍａｄｅｏｆｔｈｅｒｍｏｐｌａｓｔｉｃｃｏｍｐｏｓｉｔｅｓａｎｄｓｕｂｊｅｃｔｅｄｔｏｂｅｎｄｉｎｇ.Ｂａｓｅｄｏｎｔｈｅｓｉｎｇｌｅｐａｒａｍｅｔｅｒｐｌａｓｔｉｃｍｏｄａｌꎬｔｈｅａｓｓｏｃｉａｔｅｄｆｌｏｗｒｕｌｅｓａｎｄｔｈｅｌｉｎｅａｒｓｔｒａｉｎｈａｒｄｅｎｉｎｇｌａｗꎬｔｈｅｇｏｖｅｒｎｉｎｇｅｑｕａｔｉｏｎｓｏｆｃｕｒｖｅｄｂｅａｍｓｗｅｒｅｄｅｒｉｖｅｄａｃｃｏｒｄｉｎｇｔｏｔｈｅｂａｓｉｃｅｑｕａｔｉｏｎｓｏｆｐｌａｎｅｓｔｒｅｓｓｐｒｏｂｌｅｍｉｎｐｏｌａｒｃｏｏｒｄｉｎａｔｅｓ.Ｔｈｅａｎａｌｙｔｉｃａｌｓｏｌｕｔｉｏｎｓｏｆｓｔｒｅｓｓａｎｄｄｉｓｐｌａｃｅｍｅｎｔｗｅｒｅｔｈｅｎｏｂｔａｉｎｅｄ.Ｔｈｅｉｎｆｌｕｅｎｃｅｏｆｇｅｏｍｅｔｒｉｃａｌｓｉｚｅｏｎｓｔｒｅｓｓｄｉｓｔｒｉｂｕｔｉｏｎａｔｔｈｅｃｒｏｓｓ￣ｓｅｃｔｉｏｎｏｆｔｈｅｃｕｒｖｅｄｂｅａｍｗａｓａｎａｌｙｚｅｄ.ＡｌｓｏꎬｔｈｅｆａｉｌｕｒｅｍｏｄｅｏｆｔｈｅｃｕｒｖｅｄｂｅａｍｗａｓｊｕｄｇｅｄｉｎｖｉｒｔｕｅｏｆｔｈｅＨａｓｈｉｎｆａｉｌｕｒｅｃｒｉｔｅｒｉｏｎ.Ｔｈｅｒｅｓｕｌｔｓｄｅｍｏｎｓｔｒａｔｅｔｈｅｅｆｆｉｃｉｅｎｃｙｏｆｔｈｅｐｒｏｐｏｓｅｄｍｏｄｅｌｆｏｒｅｌａｓｔｉｃ￣ｐｌａｓｔｉｃｃｈａｒａｃｔｅｒｉｓｔｉｃｓａｎａｌｙｓｉｓｏｆｔｈｅｒｍｏｐｌａｓｔｉｃｃｏｍｐｏｓｉｔｅｃｕｒｖｅｄｂｅａｍｓｓｕｂｊｅｃｔｅｄｔｏｂｅｎｄｉｎｇ.Ａｎｄｔｈｅｆａｉｌｕｒｅｍｏｄｅｏｆｃｕｒｖｅｄｂｅａｍｓｉｓａｓｓｏｃｉａｔｅｄｗｉｔｈｔｈｅｒａｄｉｕｓ￣ｔｈｉｃｋｎｅｓｓｒａｔｉｏ.Ｋｅｙｗｏｒｄｓ㊀ＴｈｅｒｍｏｐｌａｓｔｉｃｃｏｍｐｏｓｉｔｅｓꎻＰｌａｎｅｃｕｒｖｅｄｂｅａｍꎻＥｌａｓｔｉｃ￣ｐｌａｓｔｉｃꎻＴｈｅｓｉｎｇｌｅｐａｒａｍｅｔｅｒｐｌａｓｔｉｃｍｏｄａｌꎻＨａｓｈｉｎｆａｉｌｕｒｅｃｒｉｔｅｒｉｏｎꎻＲａｄｉｕｓ￣ｔｈｉｃｋｎｅｓｓｒａｔｉｏＣｏｒｒｅｓｐｏｎｄｉｎｇａｕｔｈｏｒ:ＬＥＩＹｏｎｇＪｕｎꎬＥ￣ｍａｉｌ:ｌｅｉｙｊ１０８＠ｎｕｄｔ.ｅｄｕ.ｃｎꎬＦａｘ:＋８６￣７３１￣８７００７０２７ＴｈｅｐｒｏｊｅｃｔｓｕｐｐｏｒｔｅｄｂｙｔｈｅＮａｔｉｏｎａｌＮａｔｕｒａｌＳｃｉｅｎｃｅＦｏｕｎｄａｔｉｏｎｏｆＣｈｉｎａ(Ｎｏ.１１９０２３４８)ꎬａｎｄｔｈｅＮａｔｕｒａｌＳｃｉｅｎｃｅＦｏｕｎｄａｔｉｏｎｏｆＨｕｎａｎＰｒｏｖｉｎｃｅ(Ｎｏ.２０２０ＪＪ５６５０)ꎬａｎｄｔｈｅＳｃｉｅｎｃｅＰｒｏｊｅｃｔｏｆｔｈｅＮａｔｉｏｎａｌＵｎｉｖｅｒｓｉｔｙｏｆＤｅｆｅｎｓｅＴｅｃｈｎｏｌｏｇｙ(Ｎｏ.ＺＫ２０￣２７).Ｍａｎｕｓｃｒｉｐｔｒｅｃｅｉｖｅｄ２０２０１２０３ꎬｉｎｒｅｖｉｓｅｄｆｏｒｍ２０２１０３０８.㊀㊀引言㊀㊀热塑性复合材料具有成型周期短㊁比强度比刚度高㊁高温力学性能好㊁可熔融再加工等突出特点ꎬ已广泛应用于航空航天㊁武器装备㊁生物医学等领域[１]ꎮ在当前可重复使用运载器的需求下ꎬ热塑性复合材料具有更广阔的研究空间和应用前景[２]ꎮ曲梁结构在航天工程㊁建筑工程㊁机械工程中应用㊀第４３卷第５期刘明伟等:弯矩作用下热塑性复合材料平面曲梁弹塑性特性分析１１６３㊀㊀广泛ꎬ国内外学者针对曲梁弹塑性特性问题开展了大量研究ꎮ针对各向同性曲梁弯曲问题ꎬＤａｄｒａｓＰ[３]基于ｖｏｎＭｉｓｅｓ屈服准则和线性应变强化规律分析了曲梁弹塑性变形过程ꎮＥｒａｓｌａｎＡＮ等[４]进一步考虑了材料非线性应变强化特性ꎬ建立了曲梁弹塑性数值模型ꎮ同时ꎬＥｒａｓｌａｎＡＮ等[５￣６]基于Ｔｒｅｓｃａ屈服准则ꎬ分别利用线性应变强化规律和非线性应变强化规律ꎬ对平面曲梁弹塑性应力和变形进行了分析ꎮＦｕＪ等[７]通过建立各向同性统一强度理论ꎬ得到了曲梁临界弯矩与屈服准则的关系ꎮＷａｎｇＨ等[８]基于各向同性统一强度理论ꎬ证明了拉压异性和中间主应力效应在曲梁弹塑性力学行为研究中具有关键作用ꎮ为解决复杂载荷下各向同性曲梁弹塑性特性问题ꎬＷａｎｇＹＰ等[９]利用ｖｏｎＭｉｓｅｓ屈服准则和非线性应变强化规律建立了曲梁控制方程ꎬ并得到了应力解析解ꎮ在功能梯度曲梁弹塑性特性研究方面ꎬ余莲英等[１０]采用弹性力学逆解法ꎬ得到了端部受弯矩作用下功能梯度曲梁应力和位移解析解ꎮ为求解拉压异性功能梯度曲梁弯曲弹性应力ꎬＨｅＸ等[１１]通过将拉压弹性模量假设为两个不同的指数函数ꎬ利用幂级数法得到了应力解析解ꎮＴａｌｅｂｉｚａｄｅｈｓａｒｄａｒｉＰ等[１２]基于Ｔｉｍｏｓｈｅｎｋｏ梁理论和高阶应变梯度理论研究了碳纳米管增强功能梯度聚合物复合材料曲梁在正弦和均匀载荷作用下的静态弯曲响应ꎮＰｅｉＹＬ和ＬｉＬＸ[１３]通过定义功能梯度曲梁的广义应变和广义应力ꎬ建立了解耦的广义本构关系ꎬ得到了满足边界条件弹性解析解ꎮＮｉｅＧ等[１４]利用Ｔｒｅｓｃａ屈服准则和理想弹塑性模型得到了功能梯度纯弯曲梁弹塑性问题的解析解ꎬ确定了与弯矩相关的曲梁四种力学状态:全弹性状态㊁弹性极限状态㊁部分塑性状态和完全塑性状态ꎮＨａｓｋｕｌＭ[１５]获得了功能梯度曲梁在弯矩和温度载荷共同作用下应力和位移的解析解ꎬ并采用ｖｏｎＭｉｓｅｓ准则讨论了材料梯度和温度梯度对曲梁应力和位移的影响ꎮ在正交各向异性曲梁力学特性研究方面ꎬＴｕｔｕｎｃｕＮ[１６]利用应力函数法给出了正交各向异性平面曲梁在端部弯矩和集中力作用下应力和位移的弹性解答ꎮＨｅｉｎｚｅＰ[１７]则进一步将各向同性曲梁理论推广到各向异性曲梁中ꎬ解决了正交各向异性曲梁应力变形问题ꎮ综上所述ꎬ各向同性以及功能梯度曲梁弹塑性特性问题研究十分成熟ꎬ但热塑性复合材料是正交各向异性且具有明显弹塑性阶段[１８]ꎬ就目前而言ꎬ热塑性复合材料曲梁弹塑性特性问题研究较少ꎮ此外ꎬ由于热塑性复合材料各方向力学性能相差较大ꎬ相关试验表明[１９][２０]５０５￣５０８热塑性复合材料曲梁在不同的几何尺寸下表现出不同的失效形式ꎬ但对此类曲梁失效理论研究工作仍鲜有报道ꎮ为此ꎬ本文在平面应力假设下ꎬ基于单参数塑性模型和线性强化应变规律等ꎬ建立了弯矩作用下热塑性复合材料平面曲梁弹塑性特性分析模型ꎬ通过与有限元计算对比ꎬ验证了所建模型和计算方法的正确性ꎮ在此基础上ꎬ分析了曲梁几何尺寸如中面半径㊁径向厚度对曲梁弹塑性特性的影响ꎬ并结合Ｈａｓｈｉｎ准则对曲梁失效形式做出判断ꎬ为热塑性复合材料曲梁设计应用提供有益参考ꎮ１　热塑性复合材料平面纯弯曲梁模型建立㊀㊀考虑如图１所示的热塑性复合材料平面曲梁ꎬ其内外半径分别为ａ和ｂꎬ中面半径为ｒ０ꎬ径向厚度为ｔꎬ建立如图所示的极坐标系ｏｒθꎮ在曲梁两端作用有弯矩Ｍꎬ内外表面上无外力作用ꎬ曲梁在点(ａꎬ０)处固定ꎮ为对该曲梁弹塑性特性进行分析ꎬ作出如下基本假设:(１)曲梁在加载过程中发生弹塑性小变形ꎬ且曲梁几何尺寸变化不大ꎻ(２)曲梁处于平面应力状态ꎻ(３)热塑性复合材料被视为正交各向异性㊁线性应变强化材料ꎻ(４)纤维在基体中均匀分布且沿曲梁周向排列ꎮ图１㊀受弯矩作用的曲梁Ｆｉｇ.１㊀Ｃｕｒｖｅｄｂｅａｍｌｏａｄｉｎｇｂｙｂｅｎｄｉｎｇｍｏｍｅｎｔ曲梁仅受弯矩作用ꎬ切应变γｒθ＝０ꎬ应力和应变场只与径向坐标ｒ相关ꎮ令ｕ和ｖ分别代表切向位移和径向位移ꎬ则极坐标下应变场为εｒ＝∂ｕ∂ｒεθ＝ｕｒ＋１ｒ∂ｖ∂θγｒθ＝１ｒ∂ｕ∂θ－ｖｒ＋∂ｖ∂ｒ＝０ìîíïïïïïïïï(１)其中ꎬεｒ和εθ分别为径向应变和切向应变ꎮ在忽略体力的情况下ꎬ平衡方程为σθ－σｒ－ｒｄσｒｄｒ＝０(２)其中ꎬσｒ和σθ分别为径向应力和切向应力ꎮ当考虑塑性时ꎬ应力与应变关系为㊀１１６４㊀机㊀㊀械㊀㊀强㊀㊀度２０２１年㊀εｒ＝ａｒｒσｒ＋ａｒθσθ＋εｐｒεθ＝ａｒθσｒ＋ａθθσθ＋εｐθ(３)其中ꎬａｒｒ㊁ａθθ和ａｒθ可由曲梁柔度矩阵得到ꎬεｐｒ和εｐθ为径向塑性应变和切向塑性应变ꎬ上标ｐ代表塑性ꎮ极坐标下平面问题的应变协调方程为１ｒｄｄｒ(ｒ２ｄεθｄｒ)－ｄεｒｄｒ＝０(４)㊀㊀对式(４)积分可得ｄｄｒ(ｒεθ)－εｒ＝λ(５)其中ꎬλ为待定积分常数ꎬ将式(２)和式(３)代入到式(５)中ꎬ可得曲梁偏微分控制方程为ａθθｒ２ｄ２σｒｄｒ２＋３ａθθｒｄσｒｄｒ＋(ａθθ－ａｒｒ)σｒ＋εｐθ－εｐｒ＋ｒｄεｐθｄｒ＝λ(６)㊀㊀该控制方程适用于求解曲梁弹塑性力学响应ꎮ随着弯矩Ｍ增加ꎬ曲梁表现出三种不同的力学状态:纯弹性状态㊁部分塑性状态㊁局部失效状态ꎮ下面对这三种力学状态对应的控制方程进行求解ꎮ１ １㊀纯弹性状态㊀㊀在弹性状态下ꎬ曲梁不发生塑性变形ꎬ塑性应变εｐｒ和εｐθ为０ꎬ由式(６)可得控制方程为ａθθｒ２ｄ２σｒｄｒ２＋３ａθθｒｄσｒｄｒ＋(ａθθ－ａｒｒ)σｒ＝λ(７)㊀㊀式(７)是一个二阶变系数非齐次线性微分方程ꎬ对其求解可得纯弹性状态径向应力的表达式为σｅｒ＝Ｃ１ｋ１－ｋ２＋１ｒ１－ｋ２＋Ｃ２ｒ－ｋ１＋λ(ｋ２－１)ｋ１ａθθ(８)其中ꎬＣ１和Ｃ２为待定常数ꎬ上标ｅ代表弹性ꎬｋ１和ｋ２的表达式为ｋ１＝１＋ａｒｒａθθꎬｋ２＝２－ａｒｒａθθ(９)㊀㊀将式(８)代入到式(２)中ꎬ可得纯弹性状态下切向应力的表达式为σｅθ＝２－ｋ２ｋ１－ｋ２＋１Ｃ１ｒ１－ｋ２＋(１－ｋ１)Ｃ２ｒ－ｋ１＋λ(ｋ２－１)ｋ１ａθθ(１０)㊀㊀式(８)和式(１０)有三个待定常数Ｃ１㊁Ｃ２和λꎬ它们可由边界条件式(１１)获得σｅｒ(ｂꎬθ)＝０σｅｒ(ａꎬθ)＝０ʏｂａσｅθｒｄｒ＝－Ｍｚìîíïïïïï(１１)㊀㊀由上可知ꎬ当曲梁几何尺寸㊁材料参数以及作用弯矩确定后ꎬ曲梁的应力和应变场可唯一确定ꎮ１ ２㊀部分塑性状态１ ２ １㊀极坐标系下单参数塑性模型㊀㊀文献[２１]表明单参数塑性模型较好地描述了热塑性复合材料非线性力学行为ꎬ该模型假设热塑性复合材料在纤维增强方向上不发生塑性变形ꎮ在极坐标系下ꎬ平面应力问题中单参数塑性模型为２ｆ＝σ２ｒ＋ａ６６σ２ｒθ(１２)其中ꎬ单参数ａ６６与塑性泊松比密切相关ꎬ可由偏轴拉伸试验获得[２２]８１４￣８１８ꎮ定义等效应力σｅｑ为σｅｑ＝３ｆ(１３)㊀㊀等效塑性应变增量ｄεｐｅｑ可由式(１４)定义ꎬ如下ｄＷｐ＝σｒｄεｐｒ＋σｒθｄγｐｒ＝σｅｑｄεｐｅｑ(１４)其中ꎬｄＷｐ为等效塑性应变功增量ꎬ在纯弯曲梁弹塑性分析中切应力σｒθ恒为０ꎬ由式(１２)至式(１４)可得等效塑性应变增量ｄεｐｅｑ为ｄεｐｅｑ＝３３ｄεｐｒ(１５)㊀㊀利用相关塑性流动准则可得径向塑性应变增量ｄεｐｒ为ｄεｐｒ＝∂ｆ∂σｒｄλ＝２σｒｄλ(１６)㊀㊀对于线性应变强化材料ꎬ等效塑性应变和等效应力间关系可由Ｌｕｄｗｉｋ公式给出ꎬ如式(１７)ꎮσｅｑ＝σ０＋Ｋεｐｅｑ(１７)其中ꎬσ０为材料刚屈服时等效应力σｅｑ的值ꎬ即σ０＝３２ＹꎬＹ为热塑性复合材料垂直纤维方向屈服强度ꎬＫ为塑性常数ꎮ结合式(１２)㊁式(１３)㊁式(１５)和式(１７)可得径向塑性应变为εｐｒ＝３２(｜σｒ｜－Ｙ)２Ｋ(１８)㊀㊀由上可知ꎬ将单参数塑性模型应用于纯弯曲梁弹塑性特性分析中ꎬ曲梁在切线方向不会产生屈服ꎬ仅在径向方向上可能产生屈服ꎮ１ ２ ２㊀弹塑性应力分析㊀㊀随着弯矩的增加ꎬ曲梁塑性区域从中性面向内外表面扩展[２０]５０５－５０８ꎬ且塑性区域和弹性区域的交界面是圆弧面ꎬ令ｒ１和ｒ２分别代表塑性区域内外边界的坐标值ꎬ同一曲梁截面存在ｒ１ɤｒɤｒ２的塑性区域和ａɤｒɤｒ１以及ｒ２ɤｒɤｂ的弹性区域ꎮ将式(１８)代入到式(６)中ꎬ可得塑性区域的控制方程为ａθθｒ２ｄ２σｐｒｄｒ２＋３ａθθｒｄσｐｒｄｒ＋(ａθθ－ａｒｒ)σｐｒ＋３２(σｐｒ－Ｙ)２Ｋ＝λ(１９)㊀第４３卷第５期刘明伟等:弯矩作用下热塑性复合材料平面曲梁弹塑性特性分析１１６５㊀㊀㊀㊀该控制方程的通解为σｐｒ＝Ｃ３ｋ３－ｋ４＋１ｒ１－ｋ４＋Ｃ４ｒ－ｋ３＋３２Ｙ２ａθθＫ＋λ(ｋ４－１)ｋ３ａθθ㊀㊀ｒ１ɤｒɤｒ２(２０)其中ꎬＣ３和Ｃ４为两个待定常数ꎬｋ３和ｋ４的表达式为ｋ３＝１＋２Ｋａｒｒ＋３２２Ｋａθθꎬｋ４＝２－２Ｋａｒｒ＋３２２Ｋａθθ(２１)㊀㊀将式(２０)代入到式(２)中ꎬ可得塑性区域切向应力的表达式为σｐθ＝２－ｋ４ｋ３－ｋ４＋１Ｃ３ｒ１－ｋ４＋(１－ｋ３)Ｃ４ｒ－ｋ３＋３２Ｙ２ａθθＫ＋λ(ｋ４－１)ｋ３ａθθ㊀㊀ｒ１ɤｒɤｒ２(２２)㊀㊀弹性区域应力表达式可参考式(８)和式(１０)给出ꎬ如下σｅＩｒ＝Ｃ１ｋ１－ｋ２＋１ｒ１－ｋ２＋Ｃ２ｒ－ｋ１＋λ(ｋ２－１)ｋ１ａθθ＋η(ｒ)ｒ２ɤｒɤｂσｅＩＩｒ＝Ｃ５ｋ１－ｋ２＋１ｒ１－ｋ２＋Ｃ６ｒ－ｋ１＋λ(ｋ２－１)ｋ１ａθθ＋η(ｒ)ａɤｒɤｒ１σｅＩθ＝２－ｋ２ｋ１－ｋ２＋１Ｃ１ｒ１－ｋ２＋(１－ｋ１)Ｃ２ｒ－ｋ１＋(η(ｒ)＋ｒｄη(ｒ)ｄｒ)＋λ(ｋ２－１)ｋ１ａθθｒ２ɤｒɤｂσｅＩＩθ＝２－ｋ２ｋ１－ｋ２＋１Ｃ５ｒ１－ｋ２＋(１－ｋ１)Ｃ６ｒ－ｋ１＋(η(ｒ)＋ｒｄη(ｒ)ｄｒ)＋λ(ｋ２－１)ｋ１ａθθａɤｒɤｒ１ìîíïïïïïïïïïïïï(２３)其中ꎬ上标ｅＩ和ｅＩＩ分别代表外部弹性区域和内部弹性区域ꎮ在曲梁弹塑性状态分析中共有Ｃ１㊁Ｃ２㊁Ｃ３㊁Ｃ４㊁Ｃ５㊁Ｃ６㊁ｒ１㊁ｒ２和λ九个待定常数ꎬ它们可由边界条件和应力连续条件式(２４)获得ꎮσｅＩｒ(ｂꎬθ)＝０ꎬσｅＩＩｒ(ａꎬθ)＝０σｐｒ(ｒ１ꎬθ)＝σｅＩＩｒ(ｒ１ꎬθ)ꎬσｐｒ(ｒ２ꎬθ)＝σｅＩｒ(ｒ２ꎬθ)σｐθ(ｒ１ꎬθ)＝σｅＩＩθ(ｒ１ꎬθ)ꎬσｐθ(ｒ２ꎬθ)＝σｅＩθ(ｒ２ꎬθ)σｅＩＩｒ(ｒ１ꎬθ)＝ＹꎬσｅＩｒ(ｒ２ꎬθ)＝Ｙʏｒ１ａσｅＩＩθｒｄｒ＋ʏｒ２ｒ１σｐθｒｄｒ＋ʏｂｒ２σｅＩθｒｄｒ＝－Ｍìîíïïïïïïïï(２４)１ ３㊀局部失效状态㊀㊀在热塑性复合材料失效分析研究中ꎬＨａｓｈｉｎ准则可对纤维和基体的断裂形式进行有效区分ꎬ应用十分广泛[２２]８１４￣８１８[２３]ꎮ在极坐标系下ꎬ平面应力问题中Ｈａｓｈｉｎ失效准则表示如下ꎮ纤维拉伸或剪切失效(σθＸＴ)２＋(τｒθＳ)ȡ１㊀σθȡ０(２５)㊀㊀纤维压缩失效(σθＸＣ)２ȡ１㊀σθ<０(２６)㊀㊀基体拉伸或剪切失效(σｒＹＴ)２＋(τｒθＳ)ȡ１㊀σｒȡ０(２７)㊀㊀基体压缩失效(σｒＹＣ)２＋(σｒθＳ)ȡ１㊀σｒ<０(２８)其中ꎬＸＴ㊁ＸＣ㊁ＹＴ㊁ＹＣ和Ｓ为热塑性复合材料主方向的极限强度值ꎬ下标Ｔ和下标Ｃ分别代表拉伸方向和压缩方向ꎮ在曲梁弹塑性分析的基础上ꎬ采用Ｈａｓｈｉｎ准则对曲梁失效形式进行判断ꎬ即得到曲梁局部失效状态ꎮ１ ４㊀曲梁弹塑性位移场㊀㊀由几何方程式(１)可得热塑性复合材料平面曲梁弹塑性位移场为ｕ＝λｒθ＋αｓｉｎθｖ＝ｒεθ－λｒ－αｃｏｓθ{(２９)其中ꎬα为待定参数ꎬ可由边界条件ｖ(ａꎬ０)＝０确定ꎮ需要注意的是ꎬ由于变形协调方程式(５)在弹塑性区域均适用ꎬ故位移场在弹性和塑性区域的表达形式均一致ꎮ２㊀结果分析２ １㊀模型验证㊀㊀本节以对称纯弯曲梁为例ꎬ在弯矩为０ １１ｋＮ ｍ㊁０ １２ｋＮ ｍ和０ １３ｋＮ ｍ三种情况下ꎬ根据有限元计算结果对所建模型及计算方法进行验证和分析ꎮ设曲梁内径为８０ｍｍꎬ外径为１００ｍｍꎬ热塑性复合材料力学参数如表１所示ꎮ有限元计算采用四节点双线性平面应力四边形单元ꎬ由于分析模型具有对称性ꎬ建立了如图２所示的有限元模型ꎬ共划分了１４２５个单元ꎮ㊀１１６６㊀机㊀㊀械㊀㊀强㊀㊀度２０２１年㊀表１㊀热塑性复合材料力学参数Ｔａｂ.１㊀ＭｅｃｈａｎｉｃａｌｐａｒａｍｅｔｅｒｓｏｆｔｈｅｒｍｏｐｌａｓｔｉｃｃｏｍｐｏｓｉｔｅＥｒ/ＭＰａＥθ/ＭＰａＧｒθ/ＭＰａμＹ/ＭＰａ１０６８７１３２０００５２３６０ ３２５８６ ５３Ｋ/ＭＰａＸＴ/ＭＰａＸＣ/ＭＰａＹＴ/ＭＰａＹＣ/ＭＰａ４０００２０５０ ５１２４３ ３１００ ５７２３０２１图２㊀平面曲梁有限元模型Ｆｉｇ.２㊀Ｔｈｅｆｉｎｉｔｅｅｌｅｍｅｎｔｍｏｄｅｌｏｆｐｌａｎｅｃｕｒｖｅｄｂｅａｍ图３给出了本文与有限元计算在对称截面上应力分布的对比结果ꎬ横坐标ｒ－为无量纲坐标ꎬ其表达式如下ｒ－＝ｒ－ａｂ－ａ(３０)图３㊀曲梁对称截面应力分布Ｆｉｇ.３㊀Ｓｔｒｅｓｓｄｉｓｔｒｉｂｕｔｉｏｎａｔｔｈｅｓｙｍｍｅｔｒｉｃａｌｓｅｃｔｉｏｎｏｆｔｈｅｃｕｒｖｅｄｂｅａｍ㊀㊀由图３ａ和图３ｂ可知ꎬ当不考虑塑性时ꎬ三种弯矩作用下本文结果与有限元计算结果吻合较好ꎻ由图３ｃ和图３ｄ可知ꎬ当考虑塑性时ꎬ本文结果与有限元计算结果十分接近ꎬ两者间最大误差均不超过３％ꎬ存在该微小误差的原因是本文分析方法基于单参数塑性模型ꎬ有限元计算则基于正交各向异性Ｔｓａｉ￣Ｈｉｌｌ屈服准则ꎮ以上分析验证了本文所建模型及计算方法的正确性ꎮ此外ꎬ由图３ａ和图３ｃ可知ꎬ径向应力在曲梁中部最大ꎬ内外径处最小ꎬ且在径向方向上受拉ꎻ当弯矩相同时ꎬ在曲梁中部ꎬ考虑塑性时的径向应力均小于不考虑塑性时的径向应力ꎬ这是由于随着弯矩增加曲梁中部先屈服ꎬ屈服后的切变模量Ｋ小于弹性模量Ｅθꎬ进而导致曲梁整体刚度减小ꎮ由图３ｂ和图３ｄ可知ꎬ不考虑塑性时切向应力与归一化坐标呈近似线性关系ꎬ考虑塑性时切向应力明显地分为弹性段和塑性段ꎬ且曲梁在内表面受拉ꎬ外表面受压ꎻ当弯矩相同时ꎬ在曲梁内外表面附近ꎬ考虑塑性时的切向应力普遍大于不考虑塑性时的切向应力ꎬ这是由于当截面合力一定时ꎬ曲梁中部屈服会导致内外表面附近切向应力增大ꎮ以上分析表明ꎬ在热塑性复合材料曲梁力学特性分析中ꎬ塑性是必须考虑的因素ꎮ下面将结合具体算例分析几何参数对曲梁弹塑性应力及变形的影响ꎬ并基于Ｈａｓｈｉｎ失效准则ꎬ对曲梁失效形式进行判断ꎮ２ ２㊀中面半径ｒ０对曲梁弹塑性应力的影响㊀㊀图４分别给出了在不同中面半径ｒ０下ꎬ曲梁对称截面径向应力σｒ和切向应力σθ与归一化径向坐标ｒ－的变化曲线ꎮ在本算例中ꎬ曲梁径向厚度ｔ为２０ｍｍꎬ中面半径ｒ０分别为５０ｍｍ㊁６０ｍｍ㊁７０ｍｍ和８０ｍｍꎬ弯矩Ｍ为０ ０８ｋＮ ｍꎬ材料力学参数同上算例ꎮ㊀第４３卷第５期刘明伟等:弯矩作用下热塑性复合材料平面曲梁弹塑性特性分析１１６７㊀㊀在图４ａ中ꎬＹ表示热塑性复合材料垂直纤维方向拉伸屈服强度ꎬ超过Ｙ代表材料进入塑性状态ꎮ由图４ａ可知ꎬ在不同中面半径ｒ０下ꎬ径向应力σｒ随归一化坐标ｒ－增大而先增大后减小ꎬ且中面半径ｒ０越小ꎬ曲梁中部处于塑性状态的区域越大ꎬ相同的ｒ－坐标对应的曲梁径向应力越大ꎮ在图４ｂ中ꎬ切向应力的拐点代表曲梁弹塑性分界位置ꎮ由图４ｂ可知ꎬ切向应力σθ随归一化坐标ｒ－增大而减小ꎬ且中面半径ｒ０越小ꎬ弹塑性分界位置越靠近曲梁内外表面ꎬ内外表面处的切向应力也越大ꎮ这是由于当径向厚度ｔ相同时ꎬ曲梁中面半径ｒ０越小ꎬ曲率越大ꎬ在相同弯矩Ｍ作用下ꎬ弯曲程度越大ꎬ截面应力越大ꎬ处于塑性状态的区域面积越大ꎬ曲梁内外表面处切向应力越大ꎮ图４㊀不同中面半径下曲梁截面应力分布Ｆｉｇ.４㊀Ｓｔｒｅｓｓｄｉｓｔｒｉｂｕｔｉｏｎｏｆｃｕｒｖｅｄｂｅａｍｓｗｉｔｈｄｉｆｆｅｒｅｎｔｍｉｄ￣ｐｌａｎｅｒａｄｉｕｓ㊀㊀值得注意的是ꎬ当中面半径ｒ０从８０ｍｍ减小到５０ｍｍ时ꎬ对称截面上曲梁最大径向应力从６８ ９８ＭＰａ增加到１１３ １２ＭＰａꎬ增幅约６３ ９８％ꎻ曲梁内外表面切向应力从－１１２９ ４０ＭＰａ和１３０６ ７０ＭＰａ分别增加到－１５０５ ５０ＭＰａ和１７６９ ８０ＭＰａꎬ增幅分别为３３ ３％和３５ ４％ꎮ由以上可知ꎬ在等径向厚度曲梁分析中ꎬ中面半径ｒ０的改变会引起曲梁弹塑性状态以及截面应力大小的显著变化ꎬ故在热塑性复合材料曲梁设计中ꎬ中面半径ｒ０是一个关键参数ꎮ２ ３㊀径向厚度ｔ对曲梁弹塑性应力的影响㊀㊀为进一步分析径向厚度ｔ对曲梁对称截面弹塑性应力分布的影响ꎬ图５分别给出了不同径向厚度下曲梁对称截面径向应力σｒ和切向应力σθ随归一化坐标ｒ－的变化曲线ꎮ在本算例中ꎬ设中面半径ｒ０为６０ｍｍꎬ径向厚度ｔ分别为１６ｍｍ㊁２０ｍｍ㊁２４ｍｍ和２８ｍｍꎬ弯矩Ｍ为０ ０８ｋＮ ｍꎬ材料力学参数同上算例ꎮ由图５ａ可知ꎬ当中面半径ｒ０和作用弯矩Ｍ相同时ꎬ随着归一化径向坐标ｒ－增大不同径向厚度下对称截面径向应力σｒ先增大后减小ꎬ且径向厚度ｔ越小ꎬ曲梁处于塑性状态的区域相对越大ꎬ相同归一化坐标ｒ－下径向应力越大ꎮ由图５ｂ可知ꎬ切向应力σθ随归一化径向坐标ｒ－的增大而减小ꎻ且径向厚度ｔ越小ꎬ弹塑性分界位置越靠近曲梁内外表面ꎬ曲梁内外表面处切向应力越大ꎮ这是由于在中面半径ｒ０相同的情况下ꎬ曲梁径向厚度ｔ越小ꎬ曲梁承力面积越小ꎬ在相同弯矩Ｍ作用下ꎬ截面应力越大ꎬ处于塑性状态的区域面积相对越大ꎬ曲梁内外表面处切向应力越大ꎮ图５㊀不同径向厚度下曲梁截面应力分布Ｆｉｇ.５㊀Ｓｔｒｅｓｓｄｉｓｔｒｉｂｕｔｉｏｎｏｆｃｕｒｖｅｄｂｅａｍｓｗｉｔｈｄｉｆｆｅｒｅｎｔｒａｄｉａｌｔｈｉｃｋｎｅｓｓ㊀１１６８㊀机㊀㊀械㊀㊀强㊀㊀度２０２１年㊀㊀㊀同样值得注意的是ꎬ当曲梁径向厚度ｔ从２８ｍｍ减小到１６ｍｍꎬ曲梁最大径向应力从７２ ８８ＭＰａ增加到１２１ ９３ＭＰａꎬ增幅约６７ ２９％ꎻ曲梁内外表面切向应力从－５５８ ５４ＭＰａ和７４６ ７９ＭＰａ分别增加到－２０３３ ８０ＭＰａ和２３３３ ２０ＭＰａꎬ增幅分别为２６４ １２％和２１２ ４３％ꎮ由以上可知ꎬ在等中面半径曲梁分析中ꎬ径向厚度ｔ的微小变化会引起曲梁弹塑性状态以及截面应力大小的显著变化ꎬ故在热塑性复合材料曲梁设计中ꎬ径向厚度ｔ是一个关键参数ꎮ２ ４㊀径厚比ｒ０/ｔ与曲梁失效形式的关系㊀㊀为综合考虑中面半径ｒ０和径向厚度ｔ在曲梁设计中的作用ꎬ定义径厚比为中面半径ｒ０与径向厚度ｔ的比值ꎬ图６分别给出了截面最大径向应力以及外表面切向应力随径厚比ｒ０/ｔ的变化曲线ꎬ曲线上每一点的物理含义为在给定曲梁径厚比后曲梁发生失效时所对应的径向最大应力和外表面切向应力ꎮ在本节分析中ꎬ曲梁设内径ａ分别为１０ｍｍ㊁５０ｍｍ和１００ｍｍꎬ材料力学参数同上算例ꎮ在图６ａ中ꎬＹＴ代表热塑性复合材料垂直纤维方向的拉伸极限强度ꎬ由式(２７)可知ꎬ当径向应力σｒ超过ＹＴ时ꎬ曲梁中部因基体的拉裂而失效ꎮ在图６ｂ中ꎬＸＣ代表热塑性复合材料纤维方向的压缩极限强度ꎬ由式(２６)可知ꎬ当切向应力σθ超过ＸＣ时ꎬ曲梁外表面因纤维压溃而失效ꎮ由图６可知ꎬ在不同曲梁内径情况下ꎬ截面最大径向应力随径厚比增大而减小ꎬ外表面切向应力随径厚比增大而增大ꎮ当径厚比小于１ ５时ꎬ曲梁的最大径向应力已经超过ＹＴꎬ而外表面切向应力小于ＸＣꎬ此时曲梁的失效形式为中部开裂ꎻ当径厚比大于１ ５时ꎬ曲梁外表面切向应力已超过ＸＣꎬ而最大径向应力小于ＹＴꎬ此时曲梁的失效形式为外表面压缩失效ꎮ图６㊀最大径向应力和外表面切向应力随径厚比的变化Ｆｉｇ.６㊀Ｖａｒｉａｔｉｏｎｏｆｍａｘｉｍｕｍｒａｄｉａｌｓｔｒｅｓｓａｎｄｅｘｔｅｒｎａｌｓｕｒｆａｃｅｔａｎｇｅｎｔｉａｌｓｔｒｅｓｓｗｉｔｈｒａｄｉｕｓ￣ｔｈｉｃｋｎｅｓｓｒａｔｉｏ㊀㊀由以上分析可知ꎬ径厚比ｒ０/ｔ与曲梁的失效形式密切相关ꎬ在材料力学参数确定后ꎬ一般存在一个固定的径厚比将曲梁的失效形式分为中部开裂和外表面压缩失效两种形式ꎮ因此ꎬ当径厚比较大时ꎬ曲梁相对较细ꎬ在曲梁设计中尤其注意提高外表面的抗压能力ꎻ当径厚比较小时ꎬ曲梁相对较粗ꎬ在曲梁设计中尤其注意增强曲梁中部的抗拉能力ꎮ２ ５㊀径厚比ｒ０/ｔ对曲梁变形的影响㊀㊀图７给出了不同径厚比下曲梁对称截面的径向厚度相对变化量ｖ－随弯矩Ｍ的变化曲线ꎬ其中ꎬｖ－的表达式为ｖ－＝ｖ(０ꎬｂ)－ｖ(０ꎬａ)ｂ－ａ(３１)㊀㊀在本算例中ꎬ曲梁内径ａ为５０ｍｍꎬ径厚比Ｒ分别为５ ５０㊁３ ００和２ １６ꎬ材料力学参数同上算例ꎮ由图７可知ꎬ在不同的径厚比下ꎬ当Ｍ较小时ꎬ随着Ｍ增大ꎬｖ－呈线性增长ꎬ且径向厚度相对变化不超过１％ꎬ表明曲梁处于弹性小变形阶段ꎻ当Ｍ较大时ꎬ随着Ｍ增大ꎬｖ－出现陡升的趋势ꎬ表明曲梁进入弹塑性状态ꎮ此外ꎬ径厚比ｒ０/ｔ越小ꎬ径向厚度相对变化量的拐点越往左移ꎬ所对应的Ｍ越小ꎬ表明在曲梁内径相同的情况下径厚比ｒ０/ｔ越小ꎬ梁的承载能力越弱ꎬ更易屈服ꎮ图７㊀厚度相对变化量随弯矩的变化曲线Ｆｉｇ.７㊀Ｖａｒｉａｔｉｏｎｏｆｒｅｌａｔｉｖｅｔｈｉｃｋｎｅｓｓｖａｒｉａｔｉｏｎｗｉｔｈｍｏｍｅｎｔ３㊀结论㊀㊀本文针对弯矩作用下热塑性复合材料平面曲梁弹塑性特性问题开展了研究工作ꎮ基于单参数塑性模型㊁相关塑性流动准则和线性应变强化定律ꎬ建立了用于分析该问题的控制方程ꎬ并得到了在极坐标系下曲梁截面弹塑性应力和位移的解析解ꎮ在此基础上ꎬ结合Ｈａｓｈｉｎ失效准则确立了曲梁的三种力学状态:纯弹性状态㊁部分塑性状态和局部失效状态ꎮ最后ꎬ分析了㊀第４３卷第５期刘明伟等:弯矩作用下热塑性复合材料平面曲梁弹塑性特性分析１１６９㊀㊀曲梁中面半径㊁径向厚度对曲梁弹塑性特性的影响ꎬ研究了径厚比与曲梁失效形式的相关性ꎮ主要结论包括:１)在热塑性复合材料纯弯曲梁研究中ꎬ塑性效应显著影响梁的应力和变形ꎬ是必须考虑的因素ꎮ热塑性复合材料平面曲梁的塑性发展形式与传统材料曲梁存在很大不同ꎮ２)曲梁中面半径和径向厚度对曲梁截面弹塑性应力有很大的影响ꎬ一般来说ꎬ在弯矩相同的情况下ꎬ中面半径和径向厚度越小ꎬ曲梁截面处于塑性状态的区域越大ꎬ内外表面处的切向应力越大ꎮ３)径厚比是曲梁设计的重要参数ꎬ不同径厚比的曲梁失效形式一般不同ꎮ以本文热塑性复合材料曲梁为例ꎬ当径厚比小于１ ５时ꎬ曲梁中部开裂失效ꎻ当径厚比大于１ ５时ꎬ曲梁外表面压缩失效ꎮ４)相同弯矩情况下ꎬ径厚比越大的曲梁变形越大ꎻ弯矩显著影响曲梁变形ꎬ当弯矩较小时ꎬ曲梁径向变形很小ꎬ可忽略不计ꎻ当弯矩较大时ꎬ曲梁径向变形显著增大ꎬ产生塑性应变ꎬ不可忽略ꎮ参考文献(Ｒｅｆｅｒｅｎｃｅｓ)[１]㊀ＮｉｎｇＨꎬＬｕＮꎬＨａｓｓｅｎＡＡꎬｅｔａｌ.Ａｒｅｖｉｅｗｏｆｌｏｎｇｆｉｂｒｅｔｈｅｒｍｏｐｌａｓｔｉｃ(ＬＦＴ)ｃｏｍｐｏｓｉｔｅｓ[Ｊ].ＩｎｔｅｒｎａｔｉｏｎａｌＭａｔｅｒｉａｌｓＲｅｖｉｅｗｓꎬ２０２０ꎬ６５(３):１６４￣１８８.[２]㊀胡记强ꎬ王㊀兵ꎬ张涵其ꎬ等.热塑性复合材料构件的制备及其在航空航天领域的应用[Ｊ].宇航总体技术ꎬ２０２０ꎬ４(４):６１￣７０.ＨＵＪｉＱｉａｎｇꎬＷＡＮＧＢｉｎｇꎬＺＨＡＮＧＨａｎＱｉꎬｅｔａｌ.Ｆａｂｒｉｃａｔｉｏｎｏｆｔｈｅｒｍｏｐｌａｓｔｉｃｃｏｍｐｏｓｉｔｅｃｏｍｐｏｎｅｎｔｓａｎｄｔｈｅｉｒａｐｐｌｉｃａｔｉｏｎｉｎａｅｒｏｓｐａｃｅ[Ｊ].ＡｓｔｒｏｎａｕｔｉｃａｌＳｙｓｔｅｍｓＥｎｇｉｎｅｅｒｉｎｇＴｅｃｈｎｏｌｏｇｙꎬ２０２０ꎬ４(４):６１￣７０(ＩｎＣｈｉｎｅｓｅ).[３]㊀ＤａｄｒａｓＰ.Ｐｌａｎｅｓｔｒａｉｎｅｌａｓｔｉｃ￣ｐｌａｓｔｉｃｂｅｎｄｉｎｇｏｆａｓｔｒａｉｎ￣ｈａｒｄｅｎｉｎｇｃｕｒｖｅｄｂｅａｍ[Ｊ].ＩｎｔｅｒｎａｔｉｏｎａｌＪｏｕｒｎａｌｏｆＭｅｃｈａｎｉｃａｌＳｃｉｅｎｃｅｓꎬ２００１ꎬ４３(１):３９￣５６.[４]㊀ＥｒａｓｌａｎＡＮꎬＡｒｓｌａｎＥ.Ａｃｏｍｐｕｔａｔｉｏｎａｌｓｔｕｄｙｏｎｔｈｅｎｏｎｌｉｎｅａｒｈａｒｄｅｎｉｎｇｃｕｒｖｅｄｂｅａｍｐｒｏｂｌｅｍ[Ｊ].ＩｎｔｅｒｎａｔｉｏｎａｌＪｏｕｒｎａｌｏｆＰｕｒｅａｎｄＡｐｐｌｉｅｄＭａｔｈｅｍａｔｉｃｓꎬ２００８ꎬ４３(１):１２９￣１４３. [５]㊀ＥｒａｓｌａｎＡＮꎬＡｒｓｌａｎＥ.Ａｃｏｎｃｉｓｅａｎａｌｙｔｉｃａｌｔｒｅａｔｍｅｎｔｏｆｅｌａｓｔｉｃ‐ｐｌａｓｔｉｃｂｅｎｄｉｎｇｏｆａｓｔｒａｉｎｈａｒｄｅｎｉｎｇｃｕｒｖｅｄｂｅａｍ[Ｊ].ＡｐｐｌｉｅｄＭａｔｈｅｍａｔｉｃｓａｎｄＭｅｃｈａｎｉｃｓꎬ２００８ꎬ８８(８):６００￣６１６. [６]㊀ＡｒｓｌａｎＥꎬＥｒａｓｌａｎＡＮ.Ａｎａｌｙｔｉｃａｌｓｏｌｕｔｉｏｎｔｏｔｈｅｂｅｎｄｉｎｇｏｆａｎｏｎｌｉｎｅａｒｌｙｈａｒｄｅｎｉｎｇｗｉｄｅｃｕｒｖｅｄｂａｒ[Ｊ].ＡｃｔａＭｅｃｈａｎｉｃａꎬ２０１０ꎬ２１０(１/２):７１￣８４.[７]㊀ＦｕＪꎬＰａｎｇＭꎬＳｏｎｇＧＹꎬｅｔａｌ.Ａｎａｌｙｓｉｓｏｆｐｌａｎｅｓｔｒａｉｎｂｅｎｄｉｎｇｏｆａｓｔｒａｉｎｈａｒｄｅｎｉｎｇｃｕｒｖｅｄｂｅａｍｂａｓｅｄｏｎｕｎｉｆｉｅｄｙｉｅｌｄｃｒｉｔｅｒｉｏｎ[Ｊ].ＪｏｕｒｎａｌｏｆＳｏｕｔｈｅａｓｔＵｎｉｖｅｒｓｉｔｙ(ＥｎｇｌｉｓｈＥｄｉｔｉｏｎ)ꎬ２０１６ꎬ３２(３):３３９￣３４５.[８]㊀ＷａｎｇＨꎬＰａｎｇＭꎬＺｈａｎｇＹ.Ｅｆｆｅｃｔｓｏｆｓｔｒｅｎｇｔｈｄｉｆｆｅｒｅｎｃｅａｎｄｉｎｔｅｒｍｅｄｉａｔｅｐｒｉｎｃｉｐａｌｓｔｒｅｓｓｏｎｐｌａｎｅｓｔｒａｉｎｅｌａｓｔｉｃ￣ｐｌａｓｔｉｃｂｅｎｄｉｎｇｏｆａｃｕｒｖｅｄｂｅａｍ[Ｊ].ＡｃｔａＭｅｃｈａｎｉｃａꎬ２０１６ꎬ２２７(１２):３３５１￣３３６６. [９]㊀ＷａｎｇＹＰꎬＬｅｅＣＬꎬＨｕａｎｇＳＣ.Ｉｎｅｌａｓｔｉｃｓｔｒｅｓｓａｎａｌｙｓｉｓｏｆｃｕｒｖｅｄｂｅａｍｓｗｉｔｈｂｅｎｄｉｎｇａｎｄｓｈｅａｒｃｏｕｐｌｉｎｇ[Ｃ].ＰｒｏｃｅｅｄｉｎｇｓｏｆｔｈｅＷｏｒｌｄＣｏｎｇｒｅｓｓｏｎＣｉｖｉｌꎬＳｔｒｕｃｔｕｒａｌꎬａｎｄＥｎｖｉｒｏｎｍｅｎｔａｌＥｎｇｉｎｅｅｒｉｎｇ(ＣＳＥＥ １６)ꎬ２０１６(１０７):１￣８.[１０]㊀余莲英ꎬ张亮亮ꎬ尚兰歌ꎬ等.功能梯度曲梁弯曲问题的解析解[Ｊ].工程力学ꎬ２０１４ꎬ３１(１２):４￣１０.ＹＵＬｉａｎＹｉｎｇꎬＺＨＡＮＧＬｉａｎｇＬｉａｎｇꎬＳＨＡＮＧＬａｎＧｅꎬｅｔａｌ.Ｂｅｎｄｉｎｇｓｏｌｕｔｉｏｎｓｏｆｆｕｎｃｔｉｏｎａｌｌｙｇｒａｄｅｄｃｕｒｖｅｄ￣ｂｅａｍ[Ｊ].ＥｎｇｉｎｅｅｒｉｎｇＭｅｃｈａｎｉｃｓꎬ２０１４ꎬ３１(１２):４￣１０(ＩｎＣｈｉｎｅｓｅ).[１１]㊀ＨｅＸꎬＬｉＸꎬＬｉＷꎬｅｔａｌ.Ｂｅｎｄｉｎｇａｎａｌｙｓｉｓｏｆｆｕｎｃｔｉｏｎａｌｌｙｇｒａｄｅｄｃｕｒｖｅｄｂｅａｍｓｗｉｔｈｄｉｆｆｅｒｅｎｔｐｒｏｐｅｒｔｉｅｓｉｎｔｅｎｓｉｏｎａｎｄｃｏｍｐｒｅｓｓｉｏｎ[Ｊ].ＡｒｃｈｉｖｅｏｆＡｐｐｌｉｅｄＭｅｃｈａｎｉｃｓꎬ２０１９ꎬ８９(９):１９７３￣１９９４. [１２]㊀ＴａｌｅｂｉｚａｄｅｈｓａｒｄａｒｉＰꎬＥｙｖａｚｉａｎＡꎬＡｓｍａｅｌＭꎬｅｔａｌ.Ｓｔａｔｉｃｂｅｎｄｉｎｇａｎａｌｙｓｉｓｏｆｆｕｎｃｔｉｏｎａｌｌｙｇｒａｄｅｄｐｏｌｙｍｅｒｃｏｍｐｏｓｉｔｅｃｕｒｖｅｄｂｅａｍｓｒｅｉｎｆｏｒｃｅｄｗｉｔｈｃａｒｂｏｎｎａｎｏｔｕｂｅｓ[Ｊ].Ｔｈｉｎ￣ＷａｌｌｅｄＳｔｒｕｃｔｕｒｅｓꎬ２０２０(１５７):１０７１３９.[１３]㊀ＰｅｉＹＬꎬＬｉＬＸ.ＡｓｉｍｐｌｉｆｉｅｄｔｈｅｏｒｙｏｆＦＧｃｕｒｖｅｄｂｅａｍｓ[Ｊ].ＥｕｒｏｐｅａｎＪｏｕｒｎａｌｏｆＭｅｃｈａｎｉｃｓ￣Ａ/Ｓｏｌｉｄｓꎬ２０２１(８５):１０４１２６. [１４]㊀ＮｉｅＧꎬＺｈｏｎｇＺ.Ｃｌｏｓｅｄ￣ｆｏｒｍｓｏｌｕｔｉｏｎｓｆｏｒｅｌａｓｔｏｐｌａｓｔｉｃｐｕｒｅｂｅｎｄｉｎｇｏｆａｃｕｒｖｅｄｂｅａｍｗｉｔｈｍａｔｅｒｉａｌｉｎｈｏｍｏｇｅｎｅｉｔｙ[Ｊ].ＡｃｔａＭｅｃｈａｎｉｃａＳｏｌｉｄａＳｉｎｉｃａꎬ２０１４ꎬ２７(１):５４￣６４.[１５]㊀ＨａｓｋｕｌＭ.Ｅｌａｓｔｉｃｓｔａｔｅｏｆｆｕｎｃｔｉｏｎａｌｌｙｇｒａｄｅｄｃｕｒｖｅｄｂｅａｍｏｎｔｈｅｐｌａｎｅｓｔｒｅｓｓｓｔａｔｅｓｕｂｊｅｃｔｔｏｔｈｅｒｍａｌｌｏａｄ[Ｊ].ＭｅｃｈａｎｉｃｓＢａｓｅｄＤｅｓｉｇｎｏｆＳｔｒｕｃｔｕｒｅｓａｎｄＭａｃｈｉｎｅｓꎬ２０２０ꎬ４８(６):７３９￣７５４. [１６]㊀ＴｕｔｕｎｃｕＮ.Ｐｌａｎｅｓｔｒｅｓｓａｎａｌｙｓｉｓｏｆｅｎｄ￣ｌｏａｄｅｄｏｒｔｈｏｔｒｏｐｉｃｃｕｒｖｅｄｂｅａｍｓｏｆｃｏｎｓｔａｎｔｔｈｉｃｋｎｅｓｓｗｉｔｈａｐｐｌｉｃａｔｉｏｎｓｔｏｆｕｌｌｒｉｎｇｓ[Ｊ].ＪｏｕｒｎａｌｏｆＭｅｃｈａｎｉｃａｌＤｅｓｉｇｎꎬ１９９８ꎬ１２０(２):３６８￣３７４. [１７]㊀ＨｅｉｎｚｅＰ.Ｓｔｒｅｓｓａｎｄｓｔｒａｉｎａｎａｌｙｓｉｓｏｆｃｕｒｖｅｄｂｅａｍｓｏｆｆｉｂｒｅｒｅｉｎｆｏｒｃｅｄｐｌａｓｔｉｃ[Ｊ].ＡｃｔａＭｅｃｈａｎｉｃａＳｌｏｖａｃａꎬ２０１０ꎬ１４(２):１０８￣１１３.[１８]㊀ＣｈｉｌａｌｉＡꎬＺｏｕａｒｉＷꎬＡｓｓａｒａｒＭꎬｅｔａｌ.Ａｎａｌｙｓｉｓｏｆｔｈｅｍｅｃｈａｎｉｃａｌｂｅｈａｖｉｏｕｒｏｆｆｌａｘａｎｄｇｌａｓｓｆａｂｒｉｃｓ￣ｒｅｉｎｆｏｒｃｅｄｔｈｅｒｍｏｐｌａｓｔｉｃａｎｄｔｈｅｒｍｏｓｅｔｒｅｓｉｎｓ[Ｊ].ＪｏｕｒｎａｌｏｆＲｅｉｎｆｏｒｃｅｄＰｌａｓｔｉｃｓａｎｄＣｏｍｐｏｓｉｔｅｓꎬ２０１６ꎬ３５(１６):１２１７￣１２３２.[１９]㊀ＭａｔｓｕｏＴꎬＧｏｔｏＴꎬＴａｋａｈａｓｈｉＪ.ＩｎｖｅｓｔｉｇａｔｉｏｎａｂｏｕｔｔｈｅｆｒａｃｔｕｒｅｂｅｈａｖｉｏｒａｎｄｓｔｒｅｎｇｔｈｉｎａｃｕｒｖｅｄｓｅｃｔｉｏｎｏｆＣＦ/ＰＰｃｏｍｐｏｓｉｔｅｂｙａｔｈｉｎ￣ｃｕｒｖｅｄｂｅａｍｓｐｅｃｉｍｅｎ[Ｊ].ＡｄｖａｎｃｅｄＣｏｍｐｏｓｉｔｅＭａｔｅｒｉａｌｓꎬ２０１５ꎬ２４(３):２４９￣２６８.[２０]㊀周龙超ꎬ孔婷婷.复合材料曲梁结构弯曲失效分析[Ｊ].机械强度ꎬ２０１８ꎬ４０(２):５０５￣５０８.ＺＨＯＵＬｏｎｇＣｈａｏꎬＫＯＮＧＴｉｎｇＴｉｎｇ.Ｆａｉｌｕｒｅａｎａｌｙｓｉｓｏｆｃｏｍｐｏｓｉｔｅｃｕｒｖｅｄｂｅａｍｕｎｄｅｒｂｅｎｄｉｎｇｌｏａｄ[Ｊ].ＪｏｕｒｎａｌｏｆＭｅｃｈａｎｉｃａｌＳｔｒｅｎｇｔｈꎬ２０１８ꎬ４０(２):５０５￣５０８(ＩｎＣｈｉｎｅｓｅ).[２１]㊀ＳｕｎＣＴꎬＣｈｅｎＪＬ.Ａｓｉｍｐｌｅｆｌｏｗｒｕｌｅｆｏｒｃｈａｒａｃｔｅｒｉｚｉｎｇｎｏｎｌｉｎｅａｒｂｅｈａｖｉｏｒｏｆｆｉｂｅｒｃｏｍｐｏｓｉｔｅｓ[Ｊ].ＪｏｕｒｎａｌｏｆＣｏｍｐｏｓｉｔｅＭａｔｅｒｉａｌｓꎬ１９８９ꎬ２３(１０):１００９￣１０２０.[２２]㊀王佩艳ꎬ王富生ꎬ朱振涛ꎬ等.复合材料机械连接件的三维累积损伤研究[Ｊ].机械强度ꎬ２０１０ꎬ３２(５):８１４￣８１８.ＷＡＮＧＰｅｉＹａｎꎬＷＡＮＧＦｕＳｈｅｎｇꎬＺＨＵＺｈｅｎＴａｏꎬｅｔａｌ.３Ｄｎｕｍｅｒｉｃａｌｃａｌｃｕｌａｔｉｏｎｏｆｄａｍａｇｅａｃｃｕｍｕｌａｔｉｏｎｆｏｒｃｏｍｐｏｓｉｔｅｓｉｎｇｌｅｂｏｌｔｅｄｊｏｉｎｔ[Ｊ].ＪｏｕｒｎａｌｏｆＭｅｃｈａｎｉｃａｌＳｔｒｅｎｇｔｈꎬ２０１０ꎬ３２(５):８１４￣８１８(ＩｎＣｈｉｎｅｓｅ).[２３]㊀ＭａｒｔｉｎＲＪꎬＳａｎｄｈｕＲＳꎬＰａｌａｚｏｔｔｏＡＮ.Ｅｘｐｅｒｉｍｅｎｔａｌａｎｄａｎａｌｙｔｉｃａｌｃｏｍｐａｒｉｓｏｎｓｏｆｆａｉｌｕｒｅｉｎｔｈｅｒｍｏｐｌａｓｔｉｃｃｏｍｐｏｓｉｔｅｌａｍｉｎａｔｅｓ[Ｊ].ＥｘｐｅｒｉｍｅｎｔａｌＭｅｃｈａｎｉｃｓꎬ１９９４ꎬ３４(１):５３￣６５.。

基于弹塑性弯曲理论的圆截面梁弯曲回弹分析张锐;舒豪【摘要】论文基于弹塑性力学的基本假设,将材料简化为理想弹塑性模型,并将圆形截面梁的载荷情况简化为仅受纯弯矩载荷,并结合边界条件,研究分析了圆形截面梁的截面上弹性区和塑性区的分布及应力大小情况,在此基础上分别推导出圆形截面梁弹性变形和塑性变形对回弹的影响.通过研究发现,随着弯曲变形程度的增大,弹性变形所占比重减小,塑性变形所占比重增加.【期刊名称】《机电产品开发与创新》【年(卷),期】2019(032)002【总页数】3页(P68-70)【关键词】弹塑性变形;应力应变;回弹理论【作者】张锐;舒豪【作者单位】中机生产力促进中心,北京 100044;中机生产力促进中心,北京100044【正文语种】中文【中图分类】TB120 引言工程中的很多问题可以使用简化的模型进行分析，而圆形截面梁模型在工程简化分析中经常用到。

目前对于圆形截面梁的分析大多集中于特定载荷条件下的应力应变分析，很少有人分析变形过程中的弹、塑性区的变化规律及梁变形后的回弹问题，而这在工程上有较多的应用。

例如，冷卷螺旋弹簧成形过程中需要较大弯曲应力使得弹簧钢丝弯曲成形，成形后不可避免的存在回弹问题[1]且随着时间的变化有所变化[2]，现在主要是依靠工人的经验进行回弹的消除，没有相关的理论进行指导。

可以将弹簧钢丝简化为圆形截面梁的受力模型，使用圆形截面梁模型的弹塑性弯曲理论分析弹簧丝的弯曲过程，进而对控制弹簧成形过程中的回弹起到理论指导的作用，故研究圆形截面梁的弯曲回弹具有较大的现实意义。

1 理论推导圆形截面梁在Oxz平面内受到纯弯矩M的作用，受力分析如图1所示。

在理论分析中对圆形截面梁做如下的假设[3]。

图1 圆形截面梁受弯矩作用时受力图Fig.1 Force diagram of circular beam subjected to bending moment1.1 连续性假设即认为圆形截面梁具有连续的力学性质，其应力、应变均可以使用连续的函数进行表示。

基于ABAQUS的悬臂梁的弹塑性弯曲分析学院：航空宇航学院专业：工程力学指导教师：姓名：学号：1. 问题描述考虑端点受集中力F 作用的矩形截面的悬臂梁，如图1所示，长度l=10m ，高度h=1m ，宽度b=1m 。

材料为理想弹塑性钢材（如图2），并遵守Mises 屈服准则，屈服强度为MPa Y 380=σ，弹性模量GPa E 200=，泊松比3.0=υ。

图1 受集中力作用的悬臂梁 图2 钢材的应力-应变行为首先通过理论分析理想弹塑性材料悬臂梁的弹塑性弯曲，得到悬臂梁的弹塑性弯曲变形的规律和塑性区形状，确定弹性极限载荷e F 和塑性极限载荷Y F ；其次利用ABAQUS 模拟了该悬臂梁受集中载荷作用的变形过程，得出弹性极限载荷e F 、塑性极限载荷Y F 、塑性区形状和载荷-位移曲线，与理论分析的结果进行对比，验证有限元分析的准确性。

2. 理论分析2.1梁的弹塑性纯弯曲对于矩形截面Euler-Bernoulli 梁，受弯矩M 作用，如图3所示，根据平截面假定，有图3 矩形截面梁受弯矩M 的作用y κε= （1）其中κ为弯曲后梁轴的曲率，规定梁的挠度w 以与y 同向为正，则在小变形情况有22-dx w d =κ （2）当弯矩M 由零逐渐增大时，起初整个截面都处于弹性状态，这是Hooke 定律给出()y E E y κεσ== （3） 再由平衡方程，可得到κEI M = （4） 其中，3121bh I =是截面的惯性矩。

将EI M /=κ带入（3）式，可知 I y /M =σ显然，最外层纤维的应力值最大。

当M 增大时，最外层纤维首先达到屈服，即Y h y bh M σσ==±=22/61/ （5）这时的弯矩是整个截面处于弹性状态所能承受的最大弯矩，即为弹性极限弯矩，它等于261bh M Y e σ= （6）对应的曲率可由式（4）求得Eh EI M Y e e /2/σκ== （7）当e M M >时，梁的外层纤维的应变继续增大，但应力值保持为Y σ不再增加，塑性区将逐渐向内扩大。

热塑性复合材料建筑模板地性能分析与应用热塑性复合材料建筑模板完全由高分子纤维增强复合材料在熔融状态下通过注塑工艺一次注射成型,生产工序简便,生产过程无废水.废气和废渣排放,无噪声污染,产品可回收再利用,符合国家节能环保政策.热塑性复合材料建筑模板地核心技术在于：①应用热塑性复合材料,该材料刚韧性平衡,耐候,能实现材料地回收再利用,同时材料回收能继续注塑成型建筑模板,②精准地模具设计,为保证工程地优良施工质量,对产品地生产模具进行了特殊设计,同时考虑到热塑性产品地变形特点,还设计了一次成型便于连接地卡孔.对拉孔等特殊地连接部件.1 与传统模板比较分析1)与钢模板相比.制作工艺上,热塑性复合材料模板简单.先进.钢模板从剪板下料开始需要十多道工序和众多设备.操作人员,其生产率为5～8min/（块•人) ,这也是钢模板价格昂贵地主要原因；热塑性复合材料模板一人一机就能实现单独生产,通过一次注射成型冷却即可,其生产率约为0.5～1 min/(块•人).原料方面,热塑性复合材料模板采用普通塑胶为原料,成本低,且可以反复周转使用,大大减少周转材料地费用,降低工程成本.性能方面,热塑性复合材料可塑性好,可根据不同要求通过改变模具形式生产不同形状和规格地模板,以满足建筑不同部位.不同强度地需要,已损坏地模板回收后可重新熔化注塑成新模板,回收性能良好.使用方面,由于钢材和混凝土地热膨胀系数相近,模板与新浇筑地混凝土可牢固地粘接在一起,不易脱模,如用手锤敲击坠落容易损坏；热塑性复合材料模板由于其热膨胀系数与混凝土相差甚远,浇筑完毕后,随着温度及混凝土地凝固,其与所浇筑地混凝土自动脱离.2）与竹木模板相比.热塑性复合材料模板强度更好,可根据需要塑成不同形状,便于安装,而木模板因不能在表面钉钉子,不容易固定；竹木模板原材料为竹木,受环保政策和自然生长速度地限制,不能满足市场巨大需求,热塑性复合材料模板原材料市场充足,价格低廉,不破坏森林,利于生态环境.由此可见,这种热塑性复合材料建筑模板,在工艺技术结构性能.成本价格上是切实可行地,随着现代注塑技术与高分子技术地飞速发展,热塑性复合材料模板前景广阔.2 使用成本对比分析以一个32层房屋建筑项目为例,每层建筑面积1000 m2,模板展开面积按建筑面积地3.3倍率估算,即单层模板展开面积3300 m2,该工程总模板展开面积105600m2.完成该工程需配置竹（木）模板层数为4层,热塑性复合材料模板3层,其成本对比如表1.2所示.3 热塑性复合材料建筑模板性能分析1）物理性能良好.热塑性复合材料模板地整体性好,表面硬度高,耐摩擦,易清洗,施工温度适应范围广,耐热耐寒,抗老化,能承受各种施工负荷.2）重量轻.使用寿命长.施工轻便,省工.省时,广泛适用于高层建筑及桥梁施工；周转率高,周转次数可达80次以上.3）规格齐全,产品单体面积大.热塑性复合材料建筑模板有30多种规格,配备各种连接附件,各规格可用卡扣等附件随意拼接,满足施工需要.最大规格地模板单体面积可达到1.62m2,能有效提高施工效率.4）强度高,韧性好,不变形.热塑性复合材料模板实现了韧性和刚性间地完美平衡,抗跌落性能好,施工过程不易爆模.5)耐水,耐酸碱,耐各种腐蚀.在各种恶劣环境下可长期有效安全施工.6）易脱模.高分子材料与混凝土材料地分子结构有天然地不相容特性,可避免脱模时地强烈敲击,降低了劳动强度,提高了模板重复使用次数.7）适用于清水混凝土.热塑性复合材料模板属高分子材料,表面光洁度高,浇注物件表面光滑美观,混凝土浇注后能够达到清水墙要求,避免墙壁二次抹灰,可直接贴面装饰,工期减缩30%.8）加工性能好.可锯.可钻.可刨.可钉,纵.横向可以任意连接组合,钉.锯.钻孔等性能优于竹木胶合板.小钢模.9）施工方便.安装拆卸方便.快捷.安全,支撑操作方便,利于组织施工,加快施工进度.10）可回收再利用.能多次回收再加工,与木模板.竹胶板相比损耗低.成本低,降低了混凝土浇注成本和工程造价.11）绿色环保.生产过程无烟,无任何有毒有害气体和废气.废液.废渣地排放.4 工程案例苏州都市VIP项目位于苏州工业园区星湖街阳澄湖大道北侧50m,总建筑面积7万m2,其中地上5.5万m2,地下1.5万m2.该项目全部采用热塑性复合材料建筑模板进行施工,应用在梁.顶板.柱.剪力墙等部位（见图1）.图1 热塑性复合材料建筑模板在苏州都市VIP项目中地应用从施工现场看,前期施工效率与传统模板相当,操作熟练后施工效率提高了20%,浇注效果表面光滑,得到业主认可.由于热塑性复合材料模板应用效果显著,周边其他工程也开始应用此类模板.历经产品研发.推广,目前热塑性复合材料建筑模板已经日趋成熟,并在上海.安徽.内蒙古.山东.海南.江苏.江西.重庆等地得到广泛应用.根据产品应用反馈情况,热塑性复合材料建筑模板重复使用次数高,一般能达到50次左右,如在管理有效地情况下,可重复使用80次以上.在柱.梁.墙.现浇面等建筑部位,热塑性复合材料建筑模板都得到了良好地应用（见图2）.a 柱模b 梁模c 楼板模d 剪力墙模图2 热塑性复合材料建筑模板实际应用文/ 上海铂砾耐材料科技有限公司技术部。

北京迈达斯技术有限公司2008年7月目录1．概要 (2)2．midas Civil中的塑性铰 (3)3．桥梁资料 (4)4．输入质量 (5)5．修改边界条件 (6)6．结构的非线性特性 (7)7．定义时程分析数据 (10)8．运行结构分析 (11)9．定义分析结果函数 (11)10．查看分析结果 (12)1．概要结构抗震设计根据设防的目标不同有两种不同形式：一种是弹性设计法，另一种是弹塑性设计法。

弹性设计法主要适合在较小地震作用下的结构抗震设计，它是以结构在设计地震作用下截面的应力保持在线弹性范围内为目标，用结构的弹性强度抵抗地震荷载。

与弹性设计法不同，弹塑性设计法是允许截面应力在地震时进入塑性范围的抗震设计方法，主要是通过提高结构极限变形能力的途径改善它的抗震性能，而不是简单地增加截面尺寸、提高截面强度来加强结构的抗震能力。

《公路桥梁抗震设计规范》（报批稿）6.3.6条，根据抗震设防的原则，E2地震作用下，允许结构出现塑性，发生损伤；即在E2地震作用下，桥梁已经进入非线性工作范围，因此只有进行结构非线性时程地震反应分析才能比较真实地模拟结构实际反应。

梁柱单元的弹塑性可以采用 Bresler 建议的屈服面来表示，也可采用非线性梁柱纤维单元模拟。

《公路桥梁抗震设计规范》（报批稿）7.4.1条，E2地震作用下，一般情况下，应按式7.4.2验算潜在塑性铰区域沿纵桥向和横桥向的塑性转动能力，但是对于规则性桥梁，可按式7.4.6验算桥墩墩顶位移，对于矮墩（高宽比小于2.5）的桥墩，可不验算桥墩的变形，但应按7.3.2条验算强度。

u p θθ≤ (7.4.2)式中，p θ：在E2地震作用下，潜在塑性铰区域的塑性转角；u θ：塑性铰区域的最大容许转角。

u ∆≤∆ (7.4.6)式中，∆：在E2地震作用下墩顶的位移反应；u ∆：桥墩容许位移。

《铁路工程抗震设计规范》GB 50111-2006 中的7.3.3条，钢筋混凝土桥墩在罕遇地震作用下的弹塑性变形分析，宜采用非线性时程反应分析法，延性验算应满足下式的要求：[]u yu μμ<∆∆=max(7.3.3) 式中，u μ：非线性位移延性比；[]u μ：允许位移延性比，取值为4.8；max ∆：桥墩的非线性响应最大位移；y ∆桥墩的屈服位移。

2012 –2013 学年第2 学期课程作业《结构冲击》端部受阶跃脉冲载荷的悬臂梁的刚塑性动力响应分析一、 悬臂梁受阶跃载荷作用1. 端部受阶跃荷载的悬臂梁的刚塑性动力响应图1如图1所示，以一个具有均匀横截面的直悬臂梁AB 为例，分析其动态响应。

其中梁的长度为L ，单位长度的密度为ρ，横截面的塑性极限弯矩为M P 。

在自由端A 点突然受到横向力F （t ）的作用，此处F （t ）为不随时间变化的阶跃荷载。

由准静态下的分析容易得到，悬臂梁受端部集中力时的静态塑性失效为F C =M P /L 。

当静态集中力达到F C 时，固定端B 点将形成塑性铰，也就是该点的弯矩达到塑性极限弯矩，M B =M P 。

1)当F<F C 时，采用理想刚塑性材料假设，悬臂梁不会产生变形。

2)当F>F C 时，悬臂梁的变形机构仍然是在固定端B 点产生塑性铰，整个梁绕该塑性铰转动。

设ν为自由端A 点的速度，则对悬臂梁利用竖直方向上的动量定理，有： 1d =2dtB L F Q νρ+ （1） B Q 为固定端的支反力，以向下为正。

对固定端B 点的动量矩方程有：2p 1d =3dtL FL M νρ- （2） 则自由端A 点的加速度为p c 233d =dt FL M F F L Lνρρ--=（）（） （3） 将（3）代入（1）得固定端剪力c 1=32B Q F F -（） （4）由梁上各截面的横向加速度沿着梁的长度方向呈线性分布，既有22d d =dt dt x L ωυ-⎛⎫ ⎪⎝⎭1 （5） 得分布荷载与剪力之间的关系22d q=dtdQ dx ωρ=- （6） 对（6）式进行积分，可得梁上剪力分布：22c 220d x x ()dx=x 3()dt 2xQ x F F F F L L ωρ∙-⎛⎫=-++-- ⎪⎝⎭⎰ （7） 弯矩分布：23x c 203x x (x)=(x)=Fx 23M Q dx L L --⎛⎫- ⎪⎝⎭⎰（F-F） （8） 分布图如右图所示：图2显然，从弯矩和剪力之间的关系可知，弯矩M 应该在剪力为零的位置到达极值。