弹塑性分析讲义
- 格式:ppt
- 大小:1.30 MB
- 文档页数:28

弹塑性力学引言一、固体力学在工程中的作用工程中的各种机械都是用固体材料制造而成的、各种结构物也都是用固体材料建造的。
为了使机械结构正常使用、实现其设计的功能,首先要保证它们在工作载荷与环境作用下不发生材料的破坏或影响使用的过大的变形,即保证它们具有足够的强度、刚度和稳定性。
在设计阶段,要根据要求实现的功能,对于设计的机械结构的形式按强度要求确定其各部分的形状和尺寸,以及所需选择的材料。
要完成这样的任务,首先要解决如下基本问题:在给定形状尺寸与材料的机械结构在设计规定载荷与环境(如温度)作用下所产生的变形与应力。
对于柔性结构,如细长梁、薄板、薄壳,以及它们的组合结构,还要分析其是否会丧失稳定性。
这些都是固体力学的基本问题。
如果机械结构所受载荷或环境的作用是随时间变化的,那么,它们的振动特性也对其性能有重要的影响。
在设计时往往要对其进行模态分析,求出影响最大的各个低阶固有频率与相应的振型,以确保不会与主要的激振载荷产生共振,导致过大的交变应力与变形,影响强度和舒适性。
有些情况下还要考虑它们在瞬态或冲击载荷作用下的瞬态响应。
这些也是固体力学的基本问题。
此外、许多机械零件和结构元件在制造工程中,采用各种成型工艺,材料要产生很大的塑性变形。
如何保证加工质量,提高形状准确性、减少残余应力、避免产生裂纹、皱曲等缺陷?如何设计加工用的各种模具,加工的压力,以及整个工艺流程,这里也都有固体力学问题。
正因为工程中提出了各种各样的固体力学问题,有时还有流体力学问题,在19世纪产生了弹性力学和流体力学,才导致力学逐渐从物理学中独立出来。
工程技术发展的要求是工程力学,包括固体力学、流体力学等发展的最重要的推动力。
而工程力学的发展则大大推动了许多工程技术的飞速发展。
因此,力学是许多工程部门设计研究人员的基本素质之一。
二、力学发展概况力学曾经是物理学的一个部分,最初也是物理学中最重要的组成部分。
力学知识最早起源于人们对自然现象的观察和在生产劳动中积累的经验。



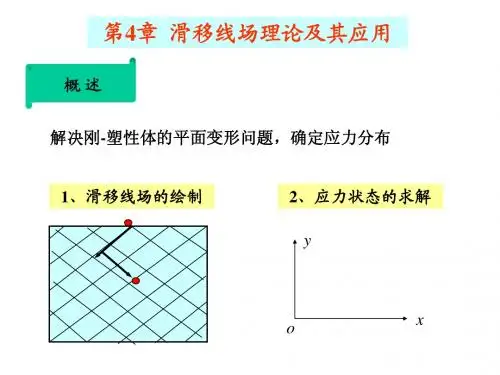




弹塑性力学弹塑性力学绪论:弹性力学也称弹性理论,主要研究弹性体在外力作用或温度变化等外界因素下所产生的应力、应变和位移,从而解决结构或机械设计中所提出的强度和刚度问题。
在研究对象上,弹性力学同材料力学和结构力学之间有一定的分工。
材料力学基本上只研究杆状构件;结构力学主要是在材料力学的基础上研究杆状构件所组成的结构,即所谓杆件系统;而弹性力学研究包括杆状构件在内的各种形状的弹性体。
弹塑性力学是固体力学的一个重要分支,是研究弹性和塑形物体变形规律的一门学科。
它推理严谨,计算结果准确,是分析和解决许多工程技术问题的基础和依据。
在弹塑性力学中,我们可以看到很多学习材料力学、结构力学等学科所熟知的参数和变量,一些解题的思路也很类似,但是我们不能等同的将弹塑性力学看成材料力学或者是结构力学来学习。
材料力学和结构力学的研究对象及问题,往往也是弹塑性力学所研究的对象及问题。
但是,在材料力学和结构力学中主要采用简化的初等理论可以描述的数学模型;在弹塑性力学中,则将采用较精确的数学模型。
有些工程问题(例如非圆形断面柱体的扭转、孔边应力集中、深梁应力分析等问题)用材料力学和结构力学的方法求解,而在弹塑性力学中是可以解决的;有些问题虽然用材料力学和结构力学的方法可以求解,但无法给出精确可靠的理论,而弹塑性力学则可以给出用初等理论所得结果可靠性与精确度的评价。
在弹塑性力学分析中,常采用如下简化假设:连续性假设、均匀各向同性、小变形假设、无初应力假设等假设。
弹塑性力学基本方程的建立需要从几何学、运动学和物理学三方面来研究。
在运动学方面,主要是建立物体的平衡条件,不仅物体整体要保持平衡,而且物体内的任何局部都要处于平衡状态。
反映这一规律的数学方程有两类,即运动微分方程和载荷的边界条件。
以上两类方程都与材料的力学性质无关,属于普适方程。
在物理学方面,则要建立应力与应变或应力与应变增量之间的关系,这种关系常称为本构关系,它描述材料在不同环境下的力学性质。

弹塑性力学第八章 塑性力学平面问题一、刚性理想塑性平面应变问题的基本方程和定解条件和弹性问题一样,平面应变问题的位移场应为()(),, ,, 0x x y y z u u x y u u x y u === (1)所研究的是柱形体,承受与轴线垂直、沿轴向均布载荷的作用,且两端约束轴向位移为零。
若物体的材料为理想塑性,则当载荷达到某定值时,物体可在载荷不变的情况下发生无限制的塑性流动,即达到塑性极限状态,简称极限状态。
下面来寻求在平面应变条件下物体在达到极限状态瞬时的响应,即应力和应变率在物体中的分布以及相应的极限载荷。
因为在刚达到极限状态的瞬时,应力率和塑性应变率均为零,且总体变形属于小量可以忽略不计。
在塑性流动过程中,塑性变形比弹性变形大得多,故可假设材料为刚性理想塑性,因而可用莱维-米赛斯塑性流动理论。
极限状态到达后,物体将继续不断产生塑性流动,几何尺寸发生显著变化,因此对继续塑性流动的研究将是材料和几何双重非线性问题,求解相当复杂。
但如果在流动过程中塑性区域在空间保持不变或几何相似,则属于稳定流动或准稳定流动问题。
这时采用空间坐标描述,则在任意瞬时仍可按塑性界限状态一样处理。
z 基本方程和定解条件根据平面应变定义和刚性理想塑性假设,在笛卡尔坐标系中塑性区应满足下列方程组: 几何方程, , y y x x x y xy v v v v x y y x εεγ∂∂∂∂===+∂∂∂∂&&& (2)本构关系,包括屈服条件()22244, (Tresca)x y xy s k k σστσ−+== (3)流动法则(莱维-米赛斯理论)()(),,2x x y y xy xy ελσσελσσγλτ=−=−=&&&第八章 塑性力学平面问题()()1 , 0 2,0 2x y z x y x y x y xy xy σσσσλσλεεσσεεγτ=+=>−−=+=&&&&&其中为塑性流动因子消去和后可得体积不可压缩条件(4)平衡方程0, 0xy xy y x x y x y ττσσ∂∂∂∂+=+=∂∂∂∂ (5)将(2)式代入(4)式,消去应变率分量,可得, 02y x x y y x y x xy v v v v x y v v x y x y σστ∂∂−−∂∂∂∂=+=∂∂∂∂+∂∂ (6)一般情况,塑性区的边界不仅指物体的实际边界,还包括两个不同区域的交界面,它可能有下列4种不同类型:给定面力的实际边界t Γ, n n n t t t στ==(7)给定表面速度的实际边界v Γ, n n t t v v v v ==(8)图8.1 给定面力边界 图8.2 给定表面速度边界图8.3 两个塑性区界面(速度间断) 图8.4 两个塑性区界面(应力间断)研究生学位课弹塑性力学电子补充讲义 姚振汉与其它塑性区的交界面y Γ可能情况1(交界面两侧切向速度发生间断,即两个塑性区相对滑动), , n n n n n n v v k σσττ−+−+−+====± (9)此时[]0t t t v v v +−=−>,即两个塑性区可以相对滑动。
弹塑性力学讲义弹塑性力学1 弹塑性的概念所谓弹塑性指的是物体在外力作用下发生变形而外力除去后变形不能完全恢复的性质。
变形中可回复的部分称为弹性变形,变形中不可回复的部分称为塑性变形。
塑性变形总是在外力的作用超过一定的限度后出现。
2 简单拉压状态下金属材料弹塑性行为及其数学模型(1)理想塑性材料的弹塑性行为σs主要特点:屈服后加载,表现出一种流动变形现象,材料失去进一步承载的能力;屈服后卸载,应力应变增量大致与弹性变形段相同。
卸载至零后再次加载,应力应变关系相当于原应力应变关系曲线在应变轴方向作了一个平移,平移量为残余塑性应变。
数学表达:Eε(0 ε εs)σ σ(ε)σ(ε ε)s s Eε( εs ε 0)σ σ(ε)(ε εs) σs(2)线性强化材料的弹塑性行为σσs主要特点:屈服后加载,材料仍有进一步承载的能力,但应力应变增量的比例较弹性段小;屈服后卸载,应力应变增量大致与弹性变形段相同。
卸载至零后再次加载,屈服应力为卸载前的应力值(较先前的屈服应力大),应力应变关系相当于原应力应变关系曲线在应变轴方向作了一个平移,平移量为残余塑性应变,同时应力轴伸长。
两种常用的强化模型数学表达:Eε(0 ε εs)σ σ(ε)σ E(ε ε)(ε ε)ss sEε( εs ε 0)σ σ(ε)σs E(ε εs)(ε εs)上述描述弹塑性材料应力应变关系的数学模型称为全量型本构关系。
显然不能代表弹塑性变形规律的全貌。
它描述了单调应力-应变过程。
为了描述弹塑性力学行为的“过程相依”,需要建立增量型本构关系。
记当前应力为σ0,应力增量为dσ,应变增量为dε,分析弹塑性行为可以得出相应的增量变形法则。
理想塑性材料的增量型弹塑性关系(1)由dσ决定dε当σs σ0 σs时,dε dσ/E 当σ0 σs时,dεdλσ0ifdσ 0 dσ/Eifdσ 0dλσ0ifdσ 0当σ0 σs时,dεdσ/Eifdσ 0(2)由dε决定dσ当σs σ0 σs时,dσ Edε0ifdε 0当σ0 σs时,dσEdεifdε 0当σ0 σs时,dσ0ifdε 0 Edεifdε 0例:已经测得某理想弹塑性材料的细杆所经受的轴向应变过程如图所示,试求此杆中的应力过程。