当前位置：文档之家 › 波动方程的简谐平面波解

波动方程的简谐平面波解

  • 格式：doc
  • 大小：2.72 MB
  • 文档页数：16

下载文档原格式

  / 16

合集下载

平面简谐波__波动方程

平面简谐波__波动方程
若振动从O 传到P所需的时间为t，在时刻t，P点处质点
的位移就是O 点处质点在t – t 时刻的位移，从相位来说，
P 点将落后于O点，其相位差为 t。
P点处质点在时刻t 的位移为：
yP (t) Acos t t' 0
平面简谐波的波动表式
因 t' x u
yP (t)
A cos
t
x u
的相位落后 。
(7)3T/4时的波形如下图中实线所示，波峰M1和M2已
分别右移3 而4 到达
y /cm
和M1' 处M。2 '
0.5 M1
M1' M2
M2'
0.4
0.2
a
0
b
0.2 10 20 30 40 50 60 70 x /cm
0.4
0.5
t=3T/4
波动方程的推导
(5)质点的最大速率
vm
波动表式的意义：
x 一定。令x=x1，则质点位移y 仅是时间t 的函数。
即
y
A cos
t
2
x1
0
上式代表x1 处质点在其平衡位置附近以角频率
作简谐运动。
y
A
O
t
t 一定。令t=t1，则质点位移y 仅是x 的函数。
平面简谐波的波动表式
即
y
A cos
t1
2
x
0
以y为纵坐标、x 为横坐标，得到一条余弦曲线，
t 2
)
球面波的余弦表式如下：
a r
cos
t
r u
0
a —r —振幅
3. 波动方程的推导
设固体细长棒的截面为S、密度为

平面简谐波的波动方程

平面简谐波的波动方程

解（１）将题给的波动方程改写成
y
0.02
cos
2
25 2
t
0.1 2
x
而波动方程的标准方程为
y
Acos 2
t T
x
二式比较得
A 0.02m
T 2 0.08s 25
2 10m
0.1
u 250m s1
T
（2）质元的振动速度为
v y 0.02 25 sin 25t 0.1xm s1
方程表示距原点为x 处的质元在不同时刻
的位移. y-t 曲线称之为位移时间曲线.
y
o
t
T
如果t 给定，则y 只是x 的函数, 这时波 动方程表示在给定时刻波射线上各振动质 元的位移，即给定时刻的波形图.
y
o
x
如果x 和t 都变化，则波动方程表示波射 线上各振动质元在不同时刻的位移，即波形 的传播.
dI Idx
I dI
x
dx
I0 I
0
ln I ax I0
I0
I
I I0eax
o
dx
x
I
I0
o
x
10.2.3 例题分析
1.一平面简谐波沿x 轴的正向传播已知波 动方程为
y 0.02cos 25t 0.1xm
求：（1）波的振幅、波长、周期及波速;
（2）质元振动的最大速度;
（3）画出t =1 s 时的波形图.
均能量密度: 能量密度在一个周期内的 平均值.
w 1
T
T 0
A2
2
sin2
t
x u
dt
1 2
A2
2
3. 能流密度

14-2平面简谐波的波动方程

14-2平面简谐波的波动方程

u
振动曲线 图形
A O
波形曲线
t A O t 0 P

t0 P
T

v
v
u x
研究 某质点位移随时间 对象 变化规律
由振动曲线可知
某时刻，波线上各质点 位移随位置变化规律
由波形曲线可知 该时刻各质点位移 波长 , 振幅A 只有t=0时刻波形才能提供初相
物理 周期 T 振幅 A 初相 0 意义
14-2 平面简谐波的波动方程
一、波函数的建立
波函数(wave function): 描述波传播媒质中不同质点的 运动规律,又称波动表达式(或波动方程).
y f x, t
依据：各质点沿波传播方 向相位依次落后. 平面波在传播过程中,波 线上的各质点都作同频率 同振幅的简谐运动—叫做 平面简谐行波(traveling wave). 波面为平面 传播中的波(相对于“驻波”而言)
x y A cos t u
(1)
P为任意点,波动表达式为
u O P( x )
x
方法2 波线上沿传播方向每走一个,相位落后2
P点相位比O落后
y P A cos(t
即
x

2π
x
y A cos(t
2π
P在 t=0 时刻过平衡位置向负向运动 ——波向左移
y(m)
0.2 O 1
t=0 P
2
yP(m) x(m)
0.2 O 0.1 0.2
t (s)
3 yO 0.2 cos(10πt π) 2 x 3 波向-x方向传播 y 0.2 cos[10 π(t ) π] 10 2 π π b) 以 P 为参考点 P yP 0 2cos( 10π t ) 2 2 波向-x方向传播 x 1 π 0 2 cos[10 π(t x ) π ] y 0 2 cos[10 π(t ) ] 10 2 10 2

16-2平面简谐波的波动方程

16-2平面简谐波的波动方程

x y ( x, t ) A cos[ (t ) 0 ] u
——细棒中平面纵波的波动方程。 解
16.2 平面简谐波和波动方程
概念检测 已知一平面简谐波的表达式为y = A cos ( a tb x )， ( a , b为正值)，则 A. 波的频率为a B. 波的传播速度为b / a C. 波长为π/ b D. 波的周期为2π/ a
0 π / 2
x y A cos[ (t ) 0 ] u π π 0.1cos( t πx ) 2 2
16.2 平面简谐波和波动方程
例题2 一列平面波以波速u沿x轴正向传播，波 长为，已知在x0= /4处的质点的振动表达式 为y0=Acos t，试写出波动方程。
16.2 平面简谐波和波动方程
填空题3. 一个余弦横波以速度u沿x轴正向传播，t 时刻 波形曲线如图所示。试分别指出图中A，B，C各点处 介质质元在该时刻的运动方向
y
A B
u
C
o
x
16.2 平面简谐波和波动方程
概念检测 下图(a)表示沿x轴正向传播的平面简谐波在t=0 时刻的波形图，则图(b)表示的是
解 “振动状态以波速传播”方法 x/4 t 时刻x处的振动状态，就是 (t ) u 时刻x0处的振动状态，因此
x/4 y A cos[( t )] u 2π π / 4 x ) A cos( t x ) A cos( t 2 u u
根据x0处的振动方程，写出波动方程
16.2 平面简谐波和波动方程
16.2 平面简谐波和波动方程
16.2.1 平面简谐波的波动方程
16.2.2 波动方程的物理意义
16.2.3 波动的微分方程

4_2_2波动方程、波的能量、声波

4_2_2波动方程、波的能量、声波
引子： 引子：悬浮的小动物 究竟是什么力量使小 动物悬浮在空中的？ 动物悬浮在空中的？ 答案在本次讲课中。 答案在本次讲课中。
§2.4 波动方程与波速
一、波动方程 简谐波的波函数为： 简谐波的波函数为： y(x,t)=Acosk(ut-x) 2 y y = k 2u2 A sin k(ut x) = kuAsin k(ut x) 2 t t y 2 y = kAsin k(ut x) = k 2 A sin k(ut x) x x 2 2 2 y 2 y =u --- 平面波的波动方程 平面波的波动方程 2 2 t x 其通解为 y = f1 ( x + ut ) + f 2 ( x ut ) --- 平面波函数 平面波函数 u 为波速
w = w
k
W V
p
1 y = E 2 x
2
2
+ w
p
1 y 1 y = ρ + E t x 2 2
2
3.能量密度 能量密度 w = w
k
+ w
p
1 y 1 y = ρ + E t 2 2 x
E ρ
2
2
棒中纵波速度 u =
E = ρu 2
1 2 y w p = ρu 2 x
1 y = ρ t 2
2
2.势能密度 势能密度
--- 与弹性（形变）有关 与弹性（形变）
考虑一棒的线变， 考虑一棒的线变， 棒长： 截面： 棒长：l ，截面：S 两端拉力： 两端拉力：由0 → F 相应形变：增至 ， 应变。 相应形变：增至l，应力 ∝ 应变。
F ES l =E F= l = kl S l l 1 2 k (l ) 势能： W p = 势能： 2

平面电磁波及其性质

平面电磁波及其性质

E＝f1(
z v
t)
B＝f1(
z v
t)
这是行波的表示式，表 示源点的振动经过一定 的时间推迟才传播到场 点。
（二）波动方程的平面简谐波解 (Simple Harmonic Wave)
A：电场振幅矢量
E＝Acos( z t) A'：磁场振幅矢量
v
：角频率
B＝A'cos( z t)
v
(
z v
t
)称为位相
E＝Acoskx cos y cos z cos t
平面波的复数形式：
E＝Aexp[i(k • r t)]
x
P(x,y,z)
k
复振幅：
r
E＝Aexp(ik • r) o
z
y
s=r k
复振幅：只关心光波在 空间的分布。
（三）平面电磁波的性质
1、横波特性：电矢量和磁矢量的方向均垂直波的传播
平面电磁波及其性质
（一）波动方程的平面波解
1、方程求解：
设光波沿z轴正向传播
y
＝x 0
x
y0
y
z0Leabharlann zz0zx
v
z
结果：2 E 1 2 E 0 v2 t 2
2E 1 2E 0 z 2 v2 t 2
令 ＝ z t, z t，代入上式则有
v
v
E＝f1
(
z v
t)
f
2
(
z v
t)
T E＝Acos(kz t)
（10－25） （10－26）
上式是一个具有单一频率、在时间和空间上 无限延伸的波。
说明2点：
在空间域中（时间轴为某
在时间域中（空间某点）

16_02_平面简谐波 波动方程


x1 点的振动方程： y1 (t ) 0.01cos[200 (t
1 ) ] ( m ) —— x 1 m 400 2
1 ) ] 2 1 (200 t ) [200 (t 2 400 2
2 1
3)
REVISED TIME: 09-10-7
-2-
CREATED BY XCH
普通物理学_程守洙_第十六章 机械波和电磁波_20090921
波数 波数 —— 波线单位长度内波的数目： k
2

x
—— 将 2 k 代入 y ( x, t ) A cos[2 ( t 3 波动方程 简谐波的波函数： y ( x, t ) A cos[ (t 对时间的二阶偏微分： 对坐标的二阶偏微分： 则：
2) 距波源 x2 2m 和 x1 1m 的两点间的振动相差
x2 点的振动方程： y2 (t ) 0.01cos(200 t ) ( m) —— x 0 2
REVISED TIME: 09-10-7 -4CREATED BY XCH

普通物理学_程守洙_第十六章 机械波和电磁波_20090921
x x0 ) 0 ] u
例题 04 如图 XCH004_135_00 所示的是一平面简谐波在 t 0 时刻的波形图，设该简谐波的频率 为 250 Hz ，且此时质点 P 的运动方向向下，求： 1) 该波的波函数； 2) 在距原点 O 为 100 m 处质点的振动方程与质点速度表达式。
x u
x u
x ) 0 ] —— 波动方程，或波函数 u 2 ， uT T
—— 波函数既是时间的周期性函数，又是空间的周期性函数。 波函数的几种表示：利用关系： 2

16-2平面简谐波 波动方程


2π x1 即 y = Acosω t λ 上式代表x1 处质点在其平衡位置附近以角频率ω 上式代表 作简谐运动。 作简谐运动。 y
A
O
t
t 一定。令t=t1，则质点位移y 仅是 的函数。 一定。 仅是x 的函数。
平面简谐波的波动表式
2π x 即 y = Acosω t1 λ
y /cm
0.5 0.4 0.2 0 0.2 0.4 0.5
M1
M2
a
10 20
b
30 40 50 60 70
x /cm
t=0
波动方程的推导
y /cm
由波形曲线图可看出： 解 由波形曲线图可看出： 0.5 0.4 (1) A=0.5cm； (2) λ=40cm； (3)由波速公式计算出 (3)由波速公式计算出
3 3
波动方程的推导
可见此点的振动相位比原点落后， 可见此点的振动相位比原点落后，相位差为 π 2，或 落后 T 4，即2×10-5s。 。 (4)该两点间的距离 (4)该两点间的距离 x = 10 cm = 0.10 m = λ 4 ，相应 的相位差为
25 × 103π t π m y = 0.1 × 10 cos 2
解
棒中的波速
u=
Y
1.9 × 1011 N m 2 = = 5.0 × 103 m/s 3 3 ρ 7.6 × 10 kg m
u 5.0 × 103 m s 1 波长 λ = = = 0.40 m 3 1 v 12.5 × 10 s
波动方程的推导
周期 T = 1 v = 8 × 10 s (1)原点处质点的振动表式 (1)原点处质点的振动表式 y0=Acosω t=0.1×10-3cos(2π×12.5×103t)m =0.1×10-3cos25×103πt m (2)波动表式

波动之平面简谐波的方程

可见：任何与波源相距为波长整数倍 当波向右传播时，就
的点(代表一个平面)都可以当整作理波课件源。 认为波源在左边。 3
{范例6.2} 平面简谐波的方程
推导平面简谐波的运动学方程，说明位移曲线和波形曲线。
基本波动动方程 u(x,t)Acos[(tx)] u
vA
v
如图所示，当波向左传播时，波动方程为
u(x,t)Acos[(tx0x)]
设波源o处质点的振动方程为u波线上任一点p的坐标为x当振动从o点传到p点时需要的时间为t时刻o处质点的位移相同因此p点在t时刻的位这就是沿x轴正方向传播的平面简谐波的运动学方程可称为基本波动方程
{范例6.2} 平面简谐波的方程
推导平面简谐波的运动学方程，说明位移曲线和波形曲线。
[解析]在波动过程中，振动相位相同的点连成 的面称为波阵面，最前面的波阵面称为波前。
方程就表示了该 时刻各质点的波 形曲线。
整理课件
2
{范例6.2} 平面简谐波的方程
推导平面简谐波的运动学方程，说明位移曲线和波形曲线。
基本波动动方程 u(x,t)Acos[(tx)]
此式在波的
利用公式ω = 2π/T和vT 波动方程可表示为
=
λu，(x,t)Acosv(t2πx)
干涉中用得 比较多。
ωt是由于时间延长而产生的相位，-2πx/λ则是由于
v
波传播到x处而滞后的相位。
A
波动方程还可以表示为
u(x,t)Acos[2π(T t x)]
此式比较 好记忆。
P0 O
x0
x
x P
如果波源不在O点而在P0点，P0到O 如果x0 = nλ(n为整数)，
的u(距x,t离)为Axc0o ，s[ P点(t 在xt 时vx刻0)的位]移为Acos[可(t得vx基)本波2动π方x0程] 。

波函数的几种不同的形式


1 2
u 2 A12 S1T
1 2
u 2 A22 S2T
S1 4r12 ; S2 4r22
r2
r1
A1r1 A2r2
所以球面波的振幅与离波源的距离成反比。
如果距波源单位距离的振幅为A则距波源r处的振幅为 A r
由于振动的相位沿波速方向随距离的增加而落后的关系， 与平面波类似，球面简谐波的波函数：
x) u
0
]d t
1 A22
2
A2,2
特点:
A2 2
s in2 [ ( t
x u
)
0
]
x, t
A、Ek Ep 相位,大小均相同；机械能不守恒。
( 注意与振动能量相区别 )
y
•c
y
•c
O
•B
x
• A 波形图
O•
•B
t
• A 振动图形
平衡位置（y = 0） E k 、 E p 最大。 振幅处（y = A） E k 、 E p 为 0。 B、若x 一定, E k 、 E p、E 均随 t 周期性变化。
t
u
显然能流是随时间周期性变化的。但它总为正值。
2)平均能流:在一个周期内能流的平均值称为平均能流。
P u S
3)能流密度:通过垂直于波动传播方向的单位面积的平均能流 称为能流密度或波的强度。
I P u 1 A2 2u
S
2
能流密度是单位时间内通过垂直于波速方向的单位截面的
平均能量。
I
1
A2 2u
1、平面波 在均匀不吸收能量的媒质中传播的平面波 在传播方向上振幅不变。
证明：因为
在一个周期
T内通过
S1和
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

波动方程的简谐平面波解在建立了波动方程之后，我们来讨论其解的形式及其特性。

1、 简谐平面波（1）波动方程的简谐平面波解声波在空间中传播，其传播方向和波阵面垂直。

平面波是波阵面是平面的声波，而简谐平面波是波阵面（对简谐波而言，波阵面也是等相位面）是平面的简谐声波。

具有任意波形的声波可以通过付里叶变换分解为多个具有不同频率的简谐平面波的叠加。

因此，简谐波传播是波动传播的基础。

一般简谐平面波的声压幅值在等相面上有一定的分布。

这里只讨论声压幅值在等相面上处处相同（均匀平面波）的简单情况，较为复杂的非等声压幅值平面波（非均匀平面波）在后面的学习中会遇到。

对一维均匀简谐平面波，声压幅值可以只用一个坐标来描述。

若取平面波的传播方向为x 轴正方向，假设波动方程中c 为常数，则波动方程的均匀简谐平面波解可以分离变量有如下形式：(,)()()p x t p x T t =，(2-23) 其中，()p x 和()T t 分别为(,)p x t 的空间坐标相关因子和时间相关因子。

将(2-23)式代入到 (2-15)中，并分离变量，得2222221()()()()d T t c d p x T t dt p x dtω==-， (2-24) 其中，2ω-为分离常数。

由(2-24)式可得两个方程：222()()0d T t T t dtω+=， (2-25) 222()()0d p x k p x dt+=。

(2-26) 其中，222k c ω=，为常数。

(2-25)式的两个特解为j t e ω和()j t e ω-，后者描述具有“负频率”的振动，无实际意义，只保留j t e ω；(2-26) 式的两个特解为jkx e 和jkx e -。

由此得到波动方程的简谐平面波解为j[t-kx]j[t+kx](,)(,)(,) =Aeep x t p x t p x t B ωω+-=++ 。

(2-27)对推导过程中几个量物理意义的讨论：① 由(2-25)的解j t e ω可以看出，ω是简谐波的圆频率，也可以理解为：在简谐波传播的过程中，介质中某一质点经过单位时间变化的相位值(对应着周期数)。

②先讨论(2-27)式的第一项(,)p x t +。

当0t =时，声压(,)p x t +在0x x =处的值(状态)为0kx Ae -；当1t t =时，在01x x t kω=+位置上，(,)p x t +的值也为0kx Ae -。

这说明由(,)p x t +描述的声波在1t 时间间隔上，由0x x =位置传播到了01x x t kω=+位置上，即声波传播了距离01x x t kω-=。

由此可知，i. (,)p x t +描述的是沿x 轴正方向传播的声压幅值为A 的均匀简谐平面波；ii. 声传播的速度是：c k ω=。

回顾c 的定义(2-9)式，当时我们还不清楚这个量的真实物理意义，在此得到了明确。

另外一种解释方法：观察者站在等相面上，等相面将向波前进方向移动。

此时，等相面的相位值不随时间变化而变化。

因此有[]0dt kx dtω-=， 即 0dxk dtω-=。

由此得dxc k dtω==。

同样道理，(,)p x t -描述的是沿x 轴负方向传播的声压幅值为A 的均匀简谐平面波。

(3) k c ω=，ω是简谐平面波的频率，c 是声波的速度，由2f ωπ=和f c λ= （f 和λ分别为声波的频率和波长）可知，2k πλ=。

波长λ的意义可以理解为：沿波传播方向，不同质点的振动状态不同，波长x λ∆=这样一个距离上，不同质点的振动状态刚好变化一个周期2k x π∆=。

也可以直观理解为：在单位长度上，不同质点的振动状态变化的周期数，亦即表示波动状态沿空间上变化的快慢。

类比时间域的周期和圆频率，λ可以理解为空间域的周期，而k 可以理解为空间域的频率。

为和时间域频率区分开来，我们把空间域的频率k 称为波数。

(4) (2-24)式中的分离变量常数取纯负数2ω-，为何不取纯正数2ω？理论上，两者都应该保留。

但当分离变量常数取纯正数2ω时，分离变量后的时间相关部分的微分方程为222()()0d T t T t dtω-=。

该方程的解为t t Ae Be ωω-+，第一项和第二项分别是随时间指数减小和增加的函数，而不代表波动，在此无意义，故此舍去。

通过求解波动方程，我们已经得到了均匀简谐平面波的声压。

下面我们进一步讨论均匀简谐平面波的质点振速，并由此给出其声强。

由运动方程(2-14)式，并分别代入沿x 轴正、反方向传播的均匀简谐平面波的声压可得质点振速为[]0011(,)=j tkx p u x t dt ex c ωρρ±∂=-±∂⎰ 。

(2-28)由(2-22)式，沿x 轴正、反方向传播的均匀简谐平面波的声强分别为00222000001Re[]Re[]1 =cos()cos()A 1 =222TT I p u dtT A A t kx t kx dt T cp cu c c ωωρρρρ+++=--==⎰⎰， (2-29a)022200001Re[]Re[]A 1 =-222TI p u dtT p cu c c ρρρ---==-=-⎰。

(2-29b)两式中，0p A =，000Au c ρ=。

(2-29b)式右端的“-”号表示声能流沿x 轴反方向传播。

由(2-29a)和 (2-29b)两式可以看出，均匀简谐平面波的声强不随距离变化，即均匀简谐平面波声强不随距离衰减。

这是其非常重要的一个物理特征。

为方便记忆，可将声功率、声压幅值、质点振速幅值及阻抗同交流电中电功率、电压幅值、电流幅值及电阻相类比。

（2）声波传播速度我们在(2-9)式中定义2sP c ρ⎛⎫∂= ⎪∂⎝⎭，经近似得到了0dP c c d ⎛== ⎝并在前一小节的讨论中知道c 的物理意义是声波在介质中的传播速度。

比值, 0()s dP d ρ代表了介质的可压缩性。

如果声波在介质中的传播过程是绝热的，在平衡态附近，给定压差dP ，若d ρ变化很小，介质中声波的传播速度就快。

否则，介质中声波的传播速度就慢。

如在金属中的声波速度较快，而在气体中声波的速度较慢。

（3）介质特性阻抗先定义介质的声阻抗率为声场中某点声压与振速之比：u p Z =。

(2-30) 其中，p 和u 分别为声场的声压和质点振速。

声阻抗率是一个复数。

它的幅值表示在介质中产生单位质点振速所需的声压大小；它的相位表示声场中声压和质点振速的相位差。

后者可以理解为给介质中的某质点加一声压，而该质点的振速没有立即反应，其状态较声压状态有一个延时（相位差）。

对于所有形式的声波，我们都可以通过(2-30)式求得其声阻抗率，或者说(2-30)式是一个对所有声波普适的定义。

对于平面波而言，声阻抗率为c Z 0ρ±=。

(2-31)其中，符号“+”为沿x 轴正向传播平面波的声阻抗率；符号“-”为沿x 轴负向传播平面波的声阻抗率。

平面波的声阻抗率有如下特点：① 平面波的声阻抗率是实数，表明声压和振速处处相同（正向波）或反相（反向波）。

这表明声能全部传播到后面位置。

声压和振速之间存在相位差时，通过计算声强可以看出相位差对能量传递的影响。

（自行验证）② 平面波的声阻抗率和声波的声压幅值无关，和声波频率无关，只和介质本身的参数密度0ρ及声速c 有关。

鉴于平面波声阻抗率是介质的特性常数，我们把平面波的声阻抗率0c ρ称为介质的特性阻抗。

其它形式声波的声阻抗率不仅和介质参数有关，还和声波参数（如频率、声压幅值大小等）相关。

不能用其阻抗率作为介质自身的特性参数。

（4）平面波在两种不同均匀介质分界面上的反射和折射声波在海洋中传播，海面是海水介质和空气介质的分界面；海底是海水介质和海底介质的分界面。

在这两个分界面上，声波将发生反射和折射。

另外，由于海水介质的折射率随深度和水平位置不同，声波也会发生折射现象。

因此，本小节的知识将是研究海水中声传播过程理论基础的一部分。

这部分知识在声学基础中也是重点掌握的知识。

因此，部分推导将略去。

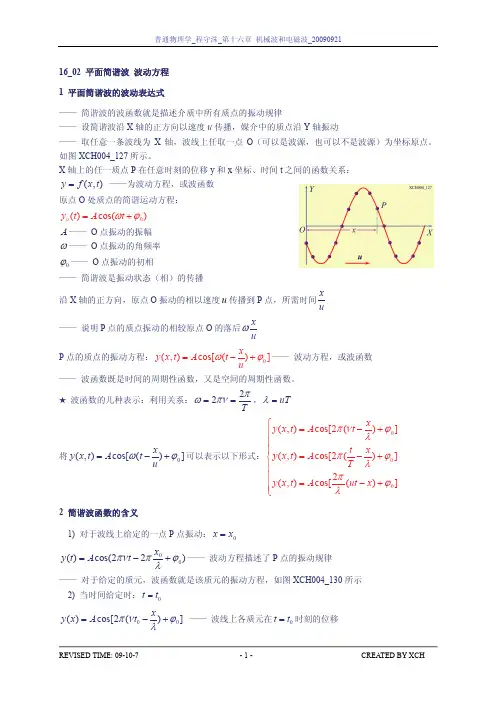
① 垂直入射在两种不同介质的分界面上，由于两介质的特性阻抗不同，声波分界面上会发生反射和折射。

在介质1中：()()x k t i r x k t i i e P e P p 111+-+=ωω()()x k t i r x k t i i e c P e c P u 1111111+--=ωωρρ 在介质2中：()x k t i t e P p 22-=ω图2.1 平面波垂直入射到两介质分界面时参数示意图()x k t i t ec P u 2222-=ωρ 界面上声压连续：()()0201,,===x x t x p t x p即t r i P P P =+。

界面上法向振速连续：()()0201,,===x x t x u t x u即221111c P c Pc P t r i ρρρ=- 由此可以推得 声压反射系数：121211221122Z Z Z Z c c c c P P R i r +-=+-==ρρρρ， (2-32) 声压透射系数：12211222222Z Z Z c c c P P D i t +=+==ρρρ。

(2-33) 其中，111Z c ρ=为介质1的特性阻抗，222Z c ρ=为介质2的特性阻抗。

由(2-32)式和(2-33)式可知，声波在分界面上反射和透射的大小决定于媒质的特性阻抗。

下面分别讨论几种极端情况，以对阻抗变化和反射、透射的关系有更深刻的认识。

i ．21Z Z =有0=R ，1=D ，表明声波没有反射，即全部透射。

也就是说，即使存在两种不同介质分界面，但只要两种介质的特性阻抗相等，那么对声传播来讲分界面就好像不存在一样。

ii ．21Z Z <有0>R ，0>D ，因为介质Ⅱ比介质Ⅰ在声学上更“硬”，这种边界称为硬边界，在硬边界上，反射波声压和入射波声压同相。

iii ．21Z Z >有0<R ，0>D ，这种边界称为软边界，在软边界上，反射波声压和入射波声压相位相反，产生半波损失现象。

而当12Z Z 时，1R =-，0D =。

iv ．21Z Z <<有1≈R ，2≈D ，介质Ⅱ对介质Ⅰ来说“绝对硬”，反射波声压和入射波声压大小相等，相位相同，所以在分界面上合成声压为入射声压的两倍，实际上发生的是全反射。

虽然声压透射系数为2，但可以计算得出介质2中的质点振速为0。

因此，在介质2中没有透射波。

下面讨论能量的透射情况。

为此先定义透射损失TL ：D Z Z D Z Z I I TL t i lg 20lg 101lg 10lg1012212-=⎪⎪⎭⎫ ⎝⎛== (2-34) 在边界是绝对硬的条件下，21Z Z <<，2≈D ，TL 值很大，表明透射能量比例很小，如声波由空气入射到水中，123570Z Z =透射损失TL=29.5dB 。