当前位置：文档之家 › 11-1简谐振动旋转矢量表示法

11-1简谐振动旋转矢量表示法

  • 格式：ppt
  • 大小：706.50 KB
  • 文档页数：17

下载文档原格式

  / 17

合集下载

第四章 振动学基础§4.2简谐振动的图示法.讲解

第四章 振动学基础§4.2简谐振动的图示法.讲解


cos(t) x 1
A2
t π 或 5π
33
由旋转矢量图可知 t π
3
v A sint
A
o A Ax
2
0.26m s1
（负号表示速度沿 Ox轴负方向）
2019/6/11
重庆邮电大学理学院
17
（3）如果物体在 x 0.05m 处时速度不等于零，而是具有 向右的初速度 v0 0.30m s，1 求其运动方程.
A
aቤተ መጻሕፍቲ ባይዱ
x
由图看出：速度超前位移 π 加速度超前速度 2
位移与加速度 Δ π 称两振动反相
若 0 称两振动同相
8、 在谐振动的合成中，用旋转矢量非常方便。
总之20，19/6旋/11 转矢量法在大学物重庆理邮电，大电学理路学院分析，等学科中有广泛15应用
例4.2.4 如图所示，一轻弹簧的右端连着一物体，弹簧的劲度
22
重庆邮电大学理学院
418
例4.2.5、一作简谐振动的物体，其振动曲
x/m
线如图所示。试写出该振动的表达式。
解：振动方程为 x Acos(t )
0.01
由振动曲线可知，振幅为 A 0.02 m
t = 0 时，
x0

A 2

0.01m
O
1
t/s
且其初始速度 v0 0
0.02
y
作旋转矢量图，如右图。

)
2
0 a v
(t )
2
v Asin(t )
x an r 2 A2
a

an
i
(t ) an i cos
大学物理-11第十一讲简谐振动、振动能量、旋转矢量法

大学物理-11第十一讲简谐振动、振动能量、旋转矢量法

振动方程 x0.15cos5tmxAcost
14
例：边长l的立方体木块浮于静水中，浸入水中部分 的高度为b。今用手将木块压下去，放手让其开始运 动。忽略水的阻力，证明木块作谐振动。 解：以水面为原点建立坐标OX。
任意时刻 F浮水(bx)l2g mgF浮ma
水 b l2g水 l2(bx)gm a
力使 减小.

mgsinmldd2t2
很小，sin mg
ml
d2
dt2
l m
f mg
d 2
dt 2

g
l

0
角谐振动
解为 0cos(t)
g T 2 l
l
g
12
例：如图所示装置，轻弹簧k =50N/m，滑轮 M =1kg,
半径 R =0.2m，物体 m =1.5kg。若将物体由平衡位置
X
P
xAcos(t)
◆可用该旋转矢量末端的投影点 P 的运动来表示简 谐振动。
16
旋转矢量法的应用
1.确定初位相 ●由初始位置 x0 确定旋转矢量两个可能的位置。 （特殊情况下只有一个位置） ●根据初始速度方向，由旋转矢量两个可能的位 置中确定初始位置，从而找出初相.。
A

Ox
17
例：确定下列情况的初位相 (a) 已知 t = 0 时，x = -A。 (b) 已知 t = 0时，x = 0，且向 x 轴正方向运动。 (c) 已知 t = 0，x = -A/2，且向 x 轴负方向运动。 (d) 已知 t = 0，x = -A/2，且向 x 轴正方向运动。
13
d2x dt2
k x0 m(1/2)m
d2x dt 2
11.振动 大学物理习题答案

11.振动 大学物理习题答案


由上述方程可解得：
（ 2）
k 2 m J / R2 ， T 2 k m J / R2 mg k mg ， 。 x cos( t ) k k m J / R2
（ 3） t 0 ， v 0 0 ， A x 0
11-4 一质量为 m 的小球在一个光滑的半径为 R 的球形碗底作微小振动， 如图 11-4 所示。 设 t＝0 时， ＝0， 小球的速度为 v0，并向右运动。求在振幅很小的情况下，小球的运动方程。 解：在切向应用牛顿定律
－ －
11-6 质量为 0.01kg 的物体，以振幅 1.010 2m 作简谐运动，其最大加速度为 4.0m·s 2。求： （1）振动的周 期； （2）物体通过平衡位置时的总能量和动能； （3）当物体的位移大小为振幅的一半时，动能和势能 各占总能量的多少？ 解： （1） a m A ，
2 2 ， ， x 0.12 cos( t ) 3 T 2 3 dx dv （ 2） v 0.12 sin( t ) ， a 0.12 2 cos( t ) dt 3 dt 3
t 0.5 s ， x 0.1039 m ， v 0.1885 m/s ， a 1.03 m/s 2
大学物理练习册—振动
11-1 一物体作简谐运动的曲线如图 11-1 所示，试求其运动方程。 解：设振动方程为 x A cos( t ) ， A 4 10 由旋转矢量法知 ，
2
x /cm 4 O
2 2
m
3 4
/4 ， 0.5 2
0.5
t /s
mg 。 k
m 图 11-3
分别取重物、滑轮和弹簧为研究对象，则有
简谐振动的旋转矢量图示法

简谐振动的旋转矢量图示法


解：
点 2 在 x = - A / 2 处 向 右 运 动 ， 试 用 旋
转 矢 量 法 求 两 质 点 的 相 位 差 。 1
3
x
2
4
3
2
A
2A
O
1
A 2
2143 3
例2、一物体沿x轴作简谐振动，振幅A=0.12m,周期 T=2s。当t=0时,物体的位移x=0.06m,且向x轴正向运
动。求: (1)简谐振动表达式;
向正方向运动,求运动方程。
解：(1) k 0.726.0s-1
m 0.02
由旋转矢量可知初相位 谐振动方程为
0 0
0.05
O
x
x0.05cos(6.0t) m
第一次经过A/2时，相位
(2) v dx 0.056.0sin(6.0t) dt
=0.3sin(6.0t) m/s
6.0t 3
OA
0, x=0.06m可
得0 3
或
3
简谐振动表达式
01
02
03
04
v0Asin00
由于t=0时质点 向x轴正向运动
0 3
因而
可知
x0.12cos(t) m
3
(2)由简谐振动的运动方程可得:
vdx0.12sin(t) m /s
dt
3
adv 0.12 2cos(t)m /s2
dt
3
在t =T/4=0.5s时，可得
A 的长度
振幅A
A 旋转的角速度
角频率ω
A 与参考方向x 的夹角
振动相位ωt+φ0
相位之差为
x1A1cos(t1)
x2A2cos(t2)
大学物理B(Ⅱ)旋转矢量

大学物理B(Ⅱ)旋转矢量

2
t 0.667s
x
A
00 7.5 A 2
A v
t0
例 一简谐运动的运动
曲线如图所示，求振动周
期.
t(s) t 0

A A2 0 A x
t 7.5
2π T T
t 7.5s
T 18s
例 已知谐振动的 A 、T ，求 1）如图简谐运动方
A＇
44
因为 v0 0 ，由旋转矢量图可知 ＇ π 4
x Acos(t ) 0.0707cos(6.0t π)
4
例2 一质量为 0.01kg 的物体作简谐运动，其振
幅为 0.08m，周期为 4s ，起始时刻物体在 x 0.04m
处，向 Ox轴负方向运动（如图）.试求
（1）t 1.0s 时，物体所处的位置和所受的力；
A/2 t ta
A 0 A x
t0
π ( π) 2π
3 33
tb
T
2π
T 3
的最短时间.
v
x/m
0.08 0.04 o 0.04 0.08
法一 设由起始位置运动到 x 0.04m 处所
需要的最短时间为 t
0.04 0.08cos(π t π) 23
t 0.667s
解法二
t 时刻
t
π3 π3
0.08 0.04 o 0.04
起始时刻
x/m
0.08
t π
3
π s1
x 0.08cos(π t π ) 23
m 0.01kg
v
x/m
0.08 0.04 o 0.04 0.08
x 0.08cos(π t π ) 23
t 1.0s 代入上式得 x 0.069m
简谐运动的旋转矢量描述法

简谐运动的旋转矢量描述法


π
4
A g a'*
h' * g'* *
t f O b*' T T f'* 3T T 5T
e
c' 4* 2*e' 4
4
-A
d*'
T 2 （旋转矢量旋转一周所需的时间）
用旋转矢量图画简谐运动的 x t 图
T 2π （旋转矢量旋转一周所需的时间）
二、旋转矢量法对相位的表示
若某时刻t，测得质点的位移为x =A/2，向OX轴负方
简谐运动的旋转 矢量表示法
一、简谐运动的旋转矢量表示法
P
t=t
t+
o
A t=0
A
x·
x
x Aco（s t ）
x Aco（s t ）
旋 转 矢量 A的
x 端点在
轴上的投
影点的运
动为简谐
运动.
x Acos(t )
用旋转矢量图画简谐运动的 x t 图
x
Ah
a
bO
c -Ad
x
x Acos(t )
向运动
M
A
O 3P
X
M
三、旋转矢量法对相位差的表示
A2
A1
O
相位差 2 1 2kπ
x
(k 0，1， 2,)
两个振动同相，步调相同
A1
O
A2
相位差 2 1 (2k 1)π
x
(k 0，1,)
两个振动反相，步调相反
例题 两个同方向、同频率的谐振动，频率为2s-1，
当第一个振子从平衡位置向正向运振动的相位差。
解：
2 1
A 2
t
o
简谐振动-旋转矢量法

简谐振动-旋转矢量法


sin2 (2 1)
y
2） 2 1 π
y A2 x A1
3）2 1 π 2
x A2
o A1
x2 A12
பைடு நூலகம்
y2 A22
1
x A1 cost
y
A2
cos(t
π) 2
A2 y
o A1 x
用 旋 转 矢 量 描 绘 振 动 合 成 图
两
相
互 垂 直 同 频 率 不 同 相
简 谐 运 动 的 合 成 图
x
x
A1 o
o
A
A2
A A1 A2
Tt
结论
A A12 A22 2A1 A2 cos(2 1 )
若两分振动同相位：
2 1 2k k 0,1, 2,
A A1 A2
若两分振动反相位:
两分振动相互加强
2 1 (2k 1) k 0,1, 2,
A A1 A2
两分振动相互减弱
再若 A1= A2 , 则 A= 0
M
A
P
x
注意：旋转矢量在第 2 象限
速度v <0
M
PA
x
注意：旋转矢量在第 2 象限
速度v <0
M
PA
x
<
注意：旋转矢量在第 3 象限
速度v 0
P x
MA
<
注意：旋转矢量在第 3 象限
速度v 0
P x
A
M
<
注意：旋转矢量在第 3 象限
速度v 0
P x
A
M
<
注意：旋转矢量在第 3 象限
速度v 0
找到谐振动的特征量，问题就解决了。
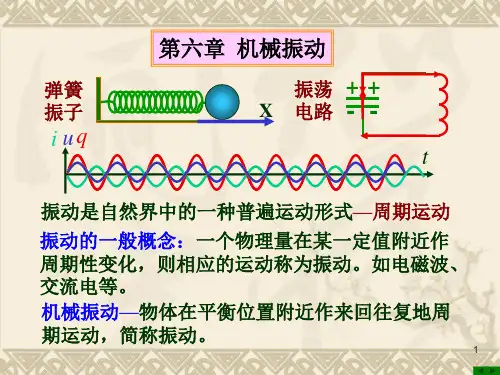
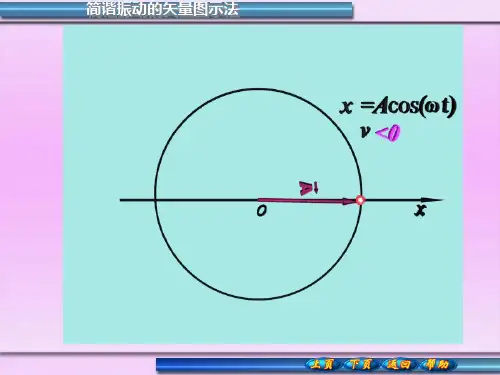
10-1 简谐振动的矢量图示法

10-1 简谐振动的矢量图示法

简谐振动的矢量图示法
简谐振动的矢量图示法
A 的长度
振幅A
A旋转的角速度
振动圆频率 O
ω
M
A
t 0
P
X
x
A 旋转的方向
逆时针方向
A 与参考方向x 的夹角 振动相位
M 点在 x 轴上投影(P点)的运动规律：
x Acos(t 0 )
矢量OM 的端点 M 所画的圆叫参考圆。 矢量 OM 0 是 t = 0 时刻的位置，它与 x 轴的夹角φ叫初相位。 简谐振动的参考圆和矢量表示方法十分形
x
A 2
A 1.0
0
t
补例 1一谐振动的振动曲线如图所示。
求：ω 、φ 以及振动方程。
x
A 2
A 1.0
0
t
补例 1一谐振动的振动曲线如图所示。
求：ω 、φ 以及振动方程。
x
A 2
A 1.0
0
t
t
=
0时
{
x 0
=
A 2
补例 1一谐振动的振动曲线如图所示
求：ω 、φ 以及振动方程。
x
A 2
A 1.0
解：已知 A = 0.12 m，T = 2s，
ω = 2π/T = π ( rad/s ).
( t =1 s ) B ’
ω
(1) 初态 t = 0 时，
x = 0.06， v ＞0， 初相 φ = －π/3 ,
-0.06
●
O 0.06
●
φ
Δφ
x (m
运动表达式为：
( t = 5/3 s) B
A(t=0)
速度v 0
P
A
x
M
§11-1简谐振动概述

§11-1简谐振动概述


A/2
0.26m / s
太原理工大学物理系
(3)如果物体在x = 0.05m处时速度不等于零, 而是 具有向右的初速度v0= 0.30m/s, 求其运动方程.
解：设 x = A cos( 6 t + 0)
2 因x0=0.05m , v0=0.3m/s A x0 2 v0 2

2.运动学方程 解微分方程可得
x A cos(t 0 )
简谐振动运动学方程
太原理工大学物理系
简谐振动的三个特征量：振幅、频率、相位
振幅 物体离开平衡位置的最大位移的绝对值 A， 由初始条件决定.
圆频率
频率 周期

k m
系统的周期性
固有的性质 称固有频率
2π
T 1
相位
由旋转矢量图知0=0 o
A x
2 v0 2
所以运动方程为： x 0.05 cos(6t )
太原理工大学物理系
(SI)
(2)求物体从初位置运动到第一次经过A/2处时的速率;
解：x=A/2时，速度方向为x轴负方向 由旋转矢量图知 相位
t

3

3
o
t时刻
A
/3
A t=0时刻
v A sin t 6.0 0.05 sin
由图看出：速度超前位移
A
A
2

A
加速度超前速度
π 2
太原理工大学物理系
(3) 计算时间简便：用熟悉的圆周运动代替三角 函数的运算。
例1 质量为m的质点和劲度系数为k的弹簧组成 的弹簧谐振子，t = 0时，质点过平衡位置且向正 方向运动。求物体运动到负二分之一振幅处所用 的最短时间。
物理-简谐振动的基本特征与旋转矢量图示法

物理-简谐振动的基本特征与旋转矢量图示法


研究简谐振动的重要性
机械振动的分类（从振动形式分） 连续振动、非连续振动； 周期振动、非周期振动…；
最简单、最基本的振动 —— 简谐运动.
简谐运动
合成 分解
复杂振动
机械振动第一讲
简谐振动的基本特征 旋转矢量图示法
一、简谐振动的定义
简谐振动
物体运动过程中，如果离开平衡位置的位 移（或角位移）按余弦函数（或正弦函数） 的规律随时间变化的运动，称为简谐振动。
三、简谐振动的三个特征量
4、振幅(A)与初相()的确定
设
注意 应根据
的符号确定 的象限范围。
三、简谐振动的三个特征量
讨论：两个同频谐振动的振动步调关系
谐振动1 x1 A1 cos(t 1 )
谐振动2 x2 A2 cos(t 2 )
相位差 (t 2 ) (t 1) 2 1
x
1）若 2 1 0
2
x轴负方向运动，而质点2在-A处。
试用旋转矢量法求这两个谐振动的初相差，及 两个质点第一次通过平衡位置的时刻。
四、简谐振动的旋转矢量图示法
小结：用旋转矢量法求相位或相位差的
O
x
第一步：由质点的位移x的值确定旋转矢量动端投影点 在x轴上的位置；
第二步：过该点作x轴的垂线，与矢量参考圆交于两点； 第三步：由质点振动速度的方向确定旋转矢量的位置。
运动学方程： 2、圆频率（ω）
最小正周期
完成一次全振动所需的时间
振动周期
振动频率 （系统固有）
三、简谐振动的三个特征量
运动学方程：
3、初相（ ）
振动速度 振动加速度
若A与确定：物体在t时刻的（x,v,a） 仅由( t + ) 决定。 称( t + ) 为物体在 t 时刻振动的相位(或)。 t =0 时的相位 ——初相位（或初相）
机械振动——简谐运动的基本概念2

机械振动——简谐运动的基本概念2

4．振动的合成(第 6 节内容) 例：一个质点沿 x 轴作简谐运动，振幅 A=0.06m，周期 T=2s，初始时刻质点位 于 x0=0.03m 处且向 x 轴正方向运动。求： （1）初相位； （2）在 x=-0.03m 处且 向向 x 轴负方向运动时物体的速度和加速度以及质点从这一位置回到平衡位置 所需要的最短时间。 解： （1）取平衡位置为坐标原点，质点的运动方程可写为
两边对时间求导，得
1 dv 1 dx m ⋅ 2v + k ⋅ 2 x =0 2 dt 2 dt
即
m⋅v
d 2x + k ⋅ xv = 0 dt 2 d 2x k + x=0 dt 2 m
令ω ＝
2
k ，则 m d 2x +ω2x = 0 2 dt
其解为
x = A′ cos(ωt + ϕ )
代入守恒方程可得 A=A’ 例 2．劲度系数为 k、原长为 l、质量为 m 的匀质弹簧，一端固定，另一端系一 质量为 M 的物体，在光滑的水平面上作直线运动，求其运动方程。
v A＝ x + 0 ω
2 0
2
二、能量平均值 定义：一个随时间变化的物理量 f(t)，在时间 T 内的平均值定义为
114
机械振动——简谐振动的基本概念
f =
1 f (t )dt T∫ 0 1 1 1 1 2 2 2 2 2 2 ∫ 2 mA ω sin (ωt + ϕ )dt = 4 mA ω = 4 kA T 0 1 1 2 1 2 1 2 2 2 ∫ 2 kA cos (ωt + ϕ )dt = 4 kA = 4 mA ω T 0
113
机械振动——简谐振动的基本概念
简谐运动的能量

§3.2 简谐振动的旋转矢量图示【VIP专享】

F kx m 2x
(0.01kg)(π s1)2 (0.069m) 1.70103 N
2
（2）由起始位置运动到 x 0.04m 处所需要
的最短时间.
v
x/m
0.08 0.04 o 0.04 0.08
解法一 设由起始位置运动到 x 0.04m 处所
需要的最短时间为 t
0.04m (0.08m) cos[(π s1)t π ]
sin0 0
0
3
简谐振动表达式 x 0.12cos( t ) m
3
因为
（2）由简谐振动的运动方程 x 0.12cos( t ) m
3
可得
v dx 0.12 sin( t ) m/s
dt
3
a dv 0.12 2 cos( t ) m/s2
dt
3
在t =T/4=0.5s时，可得
x (0.08m) cos[(π s1)t π ] 3
2
3
v0 0
π
3
A
π3
x/m
0.08 0.04 o 0.04 0.08
x (0.08m) cos[(π s1)t π ]
2
3
m 0.01kg
v
x/m
0.08 0.04 o 0.04 0.08
t 1.0s 代入上式得 x 0.069m
2
3
v
x/m
0.08 0.04 o 0.04 0.08
cos( t ) 1
23 2
t 2 或 4
233 3
又因为第一次到达- 0.04m处时，v 0
即v A sin(t ) 0
23
所以t 2
23 3
t 2s 3

大学物理第三讲：8.1.3旋转矢量法


瞬时对应
1、旋转矢量A的长度为简谐振动的振幅 2、φ为t=0时的相位（初相位） 3、（ωt+φ)为t时刻的相位 4、旋转矢量A作逆时针匀速运动（ω角速度）
5、旋转矢量A的末端在参考坐标轴上的投影点的运动即代表质 点做简谐振动。
二、旋转矢量的长处
1、用旋转矢量A来表示简谐振动的位移
x Acost 当 0时 x t曲线
x/cm
t/s
o
9
三、应用举例
已知两个同方向，同频率的简谐振动如下：
x1 5cos10t / 2 x2 5cos10t
A 50cm
5 / 4或 3 / 4
用计算法求它们合振动的振幅和初相位。
已知：A1 A2 5cm；
x/cm
1 / 2;2
t/s
o 求：1合振动的振幅：A A12 A22 ;
16
谢谢大家！ 欢迎大家多提宝贵意见！
2015.10.10
17
18
合振动的初相位：2 ?
8-18 已知两个同方向、同频率的简谐振动如下： x1 5102 cos(10t 3 / 5) SI x2 6102 cos(10t / 5) SI
（1）求它们合振动的振幅与初相位；
（2）另有一个同方向简谐振动 x3 7 102 cos(10t )SI
问值为何值时， x1 x2的振幅最大？ 问值为何值时， x2 x3的振幅最小？
0.05sin 3 0.06sin
5
0.05cos 3
5
0.06 c os
arctan2.5 1.19rad 6813
5
5

12
（2）已知：
x1 5102 cos(10t 3 / 5) SI x2 6102 cos(10t / 5) SI

11-1简谐振动旋转矢量表示法


以 o 为原 v 点旋转矢量 A 的端点在 x 轴 上的投影点的 运动为简谐运 动.
第十一章 振 动
3
大学物 理学
1111-1 简谐振动的旋转矢量表示法
ω
t =t
ωt + ϕ
v A
x
o
x = A cos(ωt + ϕ )
以 o 为原 v 点旋转矢量 A 的端点在 x 轴 上的投影点的 运动为简谐运 动.
x1 = A1 cos(ωt + ϕ1 ) x2 = A2 cos(ωt + ϕ 2 )
∆ϕ = (ωt + ϕ 2 ) − (ωt + ϕ1 )
∆ϕ = ϕ 2 − ϕ1
第十一章 振 动
10
大学物 理学
1111-1 简谐振动的旋转矢量表示法
∆ϕ = ϕ 2 − ϕ1
∆ϕ = 0 同步
∆ϕ = ±π 反相 ∆ϕ为其它
简谐运动， （1）对同一简谐运动，相位差可以给出 ） 同一简谐运动 两运动状态间变化所需的时间． 两运动状态间变化所需的时间．
x1 = A cos(ωt1 + ϕ )
x2 = A cos(ωt 2 + ϕ )
∆ϕ = (ωt2 +ϕ) −(ωt1 +ϕ)
∆t = t2 −t1 = ∆ϕ
ω
第十一章 振 动
x = 0.104m v = −0.188m / s 2 a = −1.03m / s
A
− 0.12 −0.06
t 时刻
x/m
0.12
起始时刻
15
o
π − 3
0.06
A
第十一章 振 动
ω
大学物 理学

旋转矢量法描述简谐波

速度 ．
（ ４ ） 矢 端加速 度在 Ｙ轴上 投影 的负 值 即是该 质
点 的加 速度．
（ ５ ） 该 质点动 能与 势能 的 比值
Ｅｋ
图 １
， ＭＰ＼
Ｅ 一＼ Ｏ Ｐ／
对 于第 ５点 ， 由于位 于 ５ Ｃ处 的质点 做类 简 谐振
如图 １为 旋转 矢 量 图 ， 矢端 沿 圆周运 动 的 角速
摘 要 ： 采 用 旋 转 矢 量 法 将 简 谐 波 的时 间性 与 空 间性 ， 各质点的能量 、 相位 、 位移 、 速 度 以及 加 速 度 均 反 映 到 矢 量 图中， 并利用该方法探究同方向 、 同频 率 波 的 合 成 问 题 ， 直 观 地 反 映 合 成 波 的相 关 性 质 ．
【 例 １ 】一 平 面简 谐 波沿 ｚ轴 正 向传 播 ， 已知 距
［ Ａｌ ｓ ｉ ｎ （ 一 ｈ ＋ １ ） ＋
Ａ２ ｓ ｉ ｎ（ 一 疋 ｒ ＋ ２ ）ｓ ｉ ｎｏ ａ ｏ ｚ （ １ ５ ）
波 源 ｚ一 ２ ｍ 处 的质点 Ｍ 在 ｔ ：２ ｓ 时刻 ， 向下 运动 且 相位为 ， 波长 为 ６ ０ ｍ， 周期 为 ３ ｓ ． 求：
ｙ — ｙ１ ＋ ２ （ １ ４ ）
式（ １ ２ ） 、 （ １ ３ ） 代 人式 （ １ ４ ） 整理， 得
一
所 以
［ Ａ１ ｃ ｏ ｓ （ 一 妇 十 １ ） ＋ Ａ ２ ｃ ｏ ｓ （ 一 ＋ ２ ） ］ ｏ ｏ ｓ ￣ ０ ｔ 一
鲁 Ｅ 一 （ ＼ ／ Ｏ Ｐ ） 。
＾
为波 长． 其 波上各 质点 的位移 、 速度 、 加速 度 等
学习简谐 波 的过程 中， 对 波 的相 位 、 时间性 与空 间性

4.3 简谐振动的旋转矢量法


2
大学物理
第一版
4.3 简谐振动的旋转矢量法
t t
A
o

t
x
以o 为原点 旋转矢量 A 的 端点在 x轴上的 投影点的运动为 简谐运动.
x A cos(t )
3
大学物理
第一版
4.3 简谐振动的旋转矢量法
x A cos(t )
以o 为原点 的端 旋转矢量 A 点在 x 轴上的投 影点的运动为简 谐运动.
讨论

相位差：表示两个相位之差
（1）对同一简谐运动，相位差可以给出两运 动状态间变化所需的时间．
x1 Acos( )
t t 2 t1
x2 Acos( t2 )

9
大学物理
第一版
4.3 简谐振动的旋转矢量法
vm A
A
x A cos(t )
v a

v A sin(t )
x a A 2 n
a A 2 cos( t )
7
大学物理
第一版
4.3 简谐振动的旋转矢量法
3
用旋转矢量图画简谐运动的
xt 图
8
大学物理
第一版
4.3 简谐振动的旋转矢量法
0.08
17
大学物理
第一版
4.3 简谐振动的旋转矢量法
法二
t
时刻

t
π3 π3
起始时刻
x/m
0.08
0.08 0.04
o
0.04
π π 2 1 rad s t 0.667 s t 3 2 3
18
大学物理

旋转矢量图与简谐振动的关系

旋转矢量图与简谐振动的关系背景：简谐振动是一种有规律的振动，它是在一定时间内发生的频率、幅度和相位相同的振动。

简谐振动的最大特点是振动的频率是其他振动的倍数，通常可以表示为：sin（ωt+φ），其中ω是振动频率，t是时间，φ是振动的相位。

简谐振动的根本原理是动能的循环传递，动能源可能是重力，弹簧力，电势或磁场，它们可以是振动系统的源和动力，而不断重复地传递动能，最终形成简谐振动。

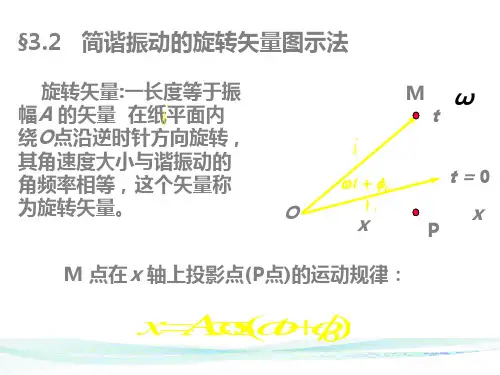
旋转矢量图是一种可以模拟物理量的数学工具，根据其使用的坐标轴有极坐标和直角坐标之分。

旋转矢量图的原理是根据分析的物理量的大小和方向，可以将其映射成极坐标和直角坐标的图形。

从旋转矢量图中可以清楚地看出物理量在时间上的变化情况，从而计算旋转矢量图所表示物理量的频率和振幅。

简谐振动与旋转矢量图之间的关系:旋转矢量图是一种可以模拟物理量的数学图表，它可以直观地表示物理量在时间上的变化情况。

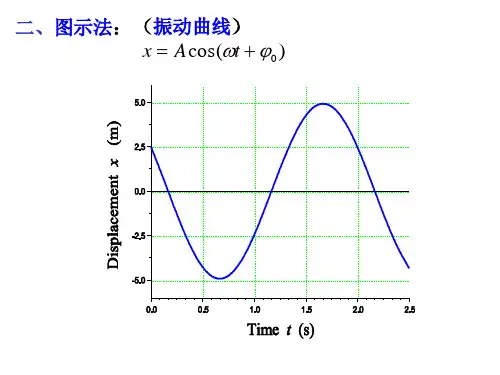
这里就是说，简谐振动的大小是旋转矢量图中表示的振幅，而简谐振动的频率是旋转矢量图中沿时间的偏移量。

当物理量的振动周期为T时，它的频率就是f=1/T，表示每秒会有一个往复，而振幅就是表示物理量每次振动的最大幅度，当振动的振幅为A时，则振动的最大大小达到2A。

旋转矢量图中沿着时间轴的偏移量可以表示为ωT，这里ω表示的是简谐振动的频率，而振幅方向反映了物理量的方向变化以及振动的相位，而这里的振幅是由动能源反复循环传递流动的结果，正是这种循环结果造成了简谐振动。

从上述分析可知，旋转矢量图是可以用来模拟简谐振动的，它既可以表示出简谐振动的频率和振幅，也可以表示出振动的方向及振动的相位，是一种比较直观和方便的模型。

结论：综上所述，简谐振动与旋转矢量图之间存在着紧密的关系，旋转矢量图可以模拟出简谐振动的频率和振幅，从而可以用来分析物理场景中一些简单的振动情况。

它的准确度和可靠性也非常高，所以在物理和数学的研究中，旋转矢量图经常作为软件和工具的重要部分，来分析和研究各种振动问题。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
大学物 理学
1111-1 简谐振动的旋转矢量表示法
旋转矢量
自Ox轴的原点 v O作一矢量 A 使 ， 它的模等于振动的 v 振幅A 振幅 ，并使矢量A 在 Oxy平面内绕点 O作逆时针方向的 逆时针方向的 匀角速转动， 匀角速转动，其角 速度 ω 与振动频率 相等， 相等，这个矢量就 叫做旋转矢量 叫做旋转矢量. 旋转矢量
5
大学物 理学
1111-1 简谐振动的旋转矢量表示法
用旋转矢量图画简谐运动的x − t图
第十一章 振 动
6
大学物 理学
1111-1 简谐振动的旋转矢量表示法
相位 ω t + ϕ
x = A cos( ω t + ϕ )
v = − A ω sin( ω t + ϕ )
相位 (位相 位相) 位相 初相位
以 o 为原 v 点旋转矢量 A 的端点在 x 轴 上的投影点的 运动为简谐运 动.
第十一章 振 动
3
大学物 理学
1111-1 简谐振动的旋转矢量表示法
ω
t =t
ωt + ϕ
v A
x
o
x = A cos(ωt + ϕ )
以 o 为原 v 点旋转矢量 A 的端点在 x 轴 上的投影点的 运动为简谐运 动.
8
大学物 理学
1111-1 简谐振动的旋转矢量表示法
x
A A2
a
b
t
tb ∆ϕ
−A
x
o
−A
v v
o A ta A
2
π ∆ϕ = 3
π 3 1 ∆t = T = T 2π 6
第十一章 振 动
9
大学物 理学
1111-1 简谐振动的旋转矢量表示法
的简谐运动， （2）对于两个同频率的简谐运动，相位 ）对于两个同频率的简谐运动 差表示它们间步调上的差异 步调上的差异（ 差表示它们间步调上的差异（解决振动合成 问题）. 问题）
超前 落后
x
x
t
x
t
o
o
o
t
第十一章 振 动
11
大学物 理学
1111-1 简谐振动的旋转矢量表示法
例 一质点沿x轴作简谐运动，振幅 轴作简谐运动， A=0.12 m，周期 ，周期T=2 s，当t=0时，质点对平衡 ， 时 位置的位移x0=0.06m.此时刻质点向 正向运动。 位置的位移 此时刻质点向x正向运动。 此时刻质点向 正向运动 试求： 试求： （1）此简谐运动的表达式 ） 解 A = 0.12 m
简谐运动， （1）对同一简谐运动，相位差可以给出 ） 同一简谐运动 两运动状态间变化所需的时间． 两运动状态间变化所需的时间．
x1 = A cos(ωt1 + ϕ )
x2 = A cos(ωt 2 + ϕ )
∆ϕ = (ωt2 +ϕ) −(ωt1 +ϕ)
∆t = t2 −t1 = ∆ϕ
ω
第十一章 振 动
x1 = A1 cos(ωt + ϕ1 ) x2 = A2 cos(ωt + ϕ 2 )
∆ϕ = (ωt + ϕ 2 ) − (ωt + ϕ1 )
∆ϕ = ϕ 2 − ϕ1
第十一章 振 动
10
大学物 理学
1111-1 简谐振动的旋转矢量表示法
∆ϕ = ϕ 2 − ϕ1
∆ϕ = 0 同步
∆ϕ = ±π 反相 ∆ϕ为其它
2π ω= = π s −1 T
t = 0， x 0 = 0.06 m
代入 x = A cos( ω t + ϕ )
第十一章 振 动
π ϕ =± 3
12
大学物 理学
1111-1 简谐振动的旋转矢量表示法 又 v = −ω A sin(ω t + ϕ )
根据题意 v 0 > 0
则 v 0 = −ω A sin(ϕ ) π 则 ϕ=−
第十一章 振 动
1
大学物 理学
1111-1 简谐振动的旋转矢量表示法
x = A cos( ω t + ϕ )
以 o 为原 v 点旋转矢量 A 的端点在 x 轴 上的投影点的 运动为简谐运 动.
第十一章 振 动
2
大学物 理学
1111-1 简谐振动的旋转矢量表示法
ω
t=0
v A
o
ϕ
x0
x
x0 = A cos ϕ
Φ (t) = ωt + ϕ
ϕ
t = 0时，Φ (t ) = ϕ
相位的意义: 表征任意时刻（ ） 相位的意义 表征任意时刻（t）物体振动状态 相貌） 物体经一周期的振动， （相貌）. 物体经一周期的振动，相位改变 2π .
第十一章 振 动
7
大学物 理学
1111-1 简谐振动的旋转矢量表示法
讨论
相位差： 相位差：表示两个相位之差
0 = 0.12 cos(ω t −
π
3
2
)
所以： 所以： ω t −
π
3
= (2 k − 1)
π
, k = 1, 2, L
t=
kπ −
π
6
ω
第十一章 振 动
16
大学物 第一次过平衡点时， 第一次过平衡点时，k=1，所以： ，所以：
5π 6 = 5 = 0.83( s ) t= π 6
v = − ω A sin(ω t + ϕ ) = − 0.12π sin(π t −
π
3
)
加速度为： 加速度为：
a = − ω 2 A cos(ω t + ϕ ) = − 0.12π cos(π t −
2
π
3
)
14
第十一章 振 动
大学物 理学
1111-1 简谐振动的旋转矢量表示法
分别代入位移、 将t=T/4=0.5s分别代入位移、速度、加 分别代入位移 速度、 速度的公式， 速度的公式，得：
第十一章 振 动
4
大学物 理学
1111-1 简谐振动的旋转矢量表示法
y
ωt + ϕ
O
v vm
v an
π ωt +ϕ + v 2
vm = Aω
v = − Aω sin(ωt + ϕ)
A
v v
x = A cos(ωt + ϕ )
v a
ω
x
an = Aω
2
2
a = − Aω cos(ωt + ϕ )
第十一章 振 动
A
x/m
− 0.12 −0.06
o
π − 3
0.06
0.12
A
第十一章 振 动
ω
起始时刻
17
x = 0.104m v = −0.188m / s 2 a = −1.03m / s
A
− 0.12 −0.06
t 时刻
x/m
0.12
起始时刻
15
o
π − 3
0.06
A
第十一章 振 动
ω
大学物 理学
1111-1 简谐振动的旋转矢量表示法
（2）从初始时刻开始第一次通过平衡位 ） 置的时刻. 置的时刻. 通过平衡位置时， 通过平衡位置时，x=0，则由位移公式： ，则由位移公式：
3
简谐运动表达式为： 简谐运动表达式为：
x = 0.12 cos(π t −
π
3
)
x/m
− 0.12 −0.06
v 0 > 0, ϕ = −
o
π
3
π − 3
0.06
0.12
A
第十一章 振 动
ω
13
大学物 理学
1111-1 简谐振动的旋转矢量表示法
质点的位置、速度、 （2）t = T /4 时，质点的位置、速度、加速度 ） 此简谐运动的速度为： 此简谐运动的速度为：