专题05 倍长中线问题(解析版)

3

1全等模型3：倍长中线模型一、模型介绍

（一）基本模型已知：在△ABC中，AD是BC边上的中线，延

长AD到点E，使ED＝AD，连接BE．

结论1：△ACD≌△EBD．

已知：在△ABC中，点D是BC边的中点，点E

是AB边上一点，连接ED，延长ED到点F，

使DF＝DE，连接CF．

结论2：△BDE≌△CDF．

（二）结论推导

结论1：△ACD≌△EBD．

证明：∵AD是BC边上的中线，∴CD＝BD．

∵∠ADC＝∠EDB，AD＝ED，∴△ACD≌△EBD．

结论2：△BDE≌△CDF．

证明：∵点D是BC边的中点，∴BD＝CD．

∵∠BDE＝∠CDF，DE＝DF，∴△BDE≌△CDF．

（三）解题技巧

遇到中点或中线，则考虑使用“倍长中线模型”，即延长中线，使所延长部分与中线相等，然后连接相应的顶

点，构造出全等三角形．

典型例题：

例1如图，在Rt△ABC中，∠BAC＝90°，AD是斜边BC上的中

线，求证：AD＝12BC．

考点分析：全等三角形的判定与性质，平行线

的判定与性质．

思路点拨：倍长AD到点E，连接CE．先证△ABD≌△ECD，

得AB＝CE，∠B＝∠ECD，再证△ABC≌△CEA，可得结论．A

BDC

E

A

BDCFE3

2例2如图，△ABC≌△ADE，∠ACB＝∠AED＝90°，连接EC并

延长，交BD于点F，求证：F为BD的中点．

考点分析：

全等三角形的判定与性质，平行线的判定与性

质，等腰三角形的判定与性质．

思路点拨：

过点B作BG∥DE，交EF的延长线于点G．先

根据△ABC≌△ADE，得AC＝AE，BC＝DE，

再证BG＝BC，最后证△BGF≌△DEF即可．

例3如图，△ABC和△DEC都是等腰直角三角形，∠ACB＝∠DCE

＝90°，连接AD，BE，点F为线段AD的中点，连接CF，猜

想BE与CF的数量关系与位置关系，并说明理由．

考点分析：

全等三角形的判定与性质，平行线的判定与性

质，等腰直角三角形的性质．

思路点拨：

倍长CF到点G，连接AG．先证△AFG≌△DFC，得AG＝CD，∠AGF＝∠DCF，再证

倍长中线法

知识网络详解：

中线是三角形中的重要线段之一，在利用中线解决几何问题时，常常采用“倍长中线法”添加辅助线．

所谓倍长中线法，就是将三角形的中线延长一倍，以便构造出全等三角形，从而运用全等三角形的有关知识来解决问题的方法．

倍长中线法的过程：延长某某到某点，使某某等于某某，使什么等于什么（延长的那一条），用SAS证全等（对顶角）

倍长中线最重要的一点，延长中线一倍，完成SAS全等三角形模型的构造。

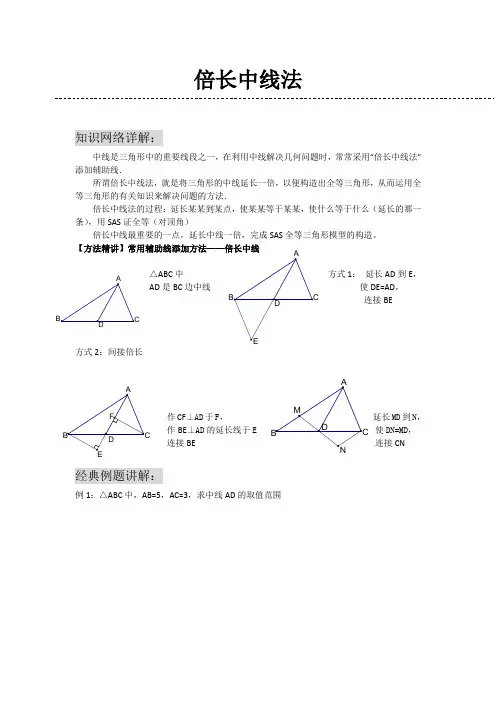
【方法精讲】常用辅助线添加方法——倍长中线

△ABC中

方式1： 延长AD到E，

AD是BC边中线

使DE=AD，

连接BE

方式2：间接倍长

作CF⊥AD于F， 延长MD到N，

作BE⊥AD的延长线于E 使DN=MD，

连接BE 连接CN

经典例题讲解：

例1：△ABC中，AB=5，AC=3，求中线AD的取值范围

DABCEDABCFEDCBANDCBAM例2：已知在△ABC中，AB=AC，D在AB上，E在AC的延长线上，DE交BC于F，且DF=EF，求证：BD=CE

例3：已知在△ABC中，AD是BC边上的中线，E是AD上一点，且BE=AC，延长BE交AC于F，求证：AF=EF

例4：已知：如图，在ABC中，ACAB，D、E在BC上，且DE=EC，过D作BADF//交AE于点F，DF=AC.

求证：AE平分BAC

FEDABCFECABDABFDEC例5：已知CD=AB，∠BDA=∠BAD，AE是△ABD的中线，求证：∠C=∠BAE

初⼆数学倍长中线全等之倍长中线和截长补短

定 义

⽰例剖析

倍长中线：即延长三⾓形的中线，使得延长后的线段是原中线的两倍．

其⽬的是构造⼀对对顶的全等三⾓形； 其本质是转移边和⾓．E

D

A

B

C

其中BD CD =，延长AD 使得DE AD =，则BDE CDA △≌△．

【例1】 已知ABC △中，AD 平分BAC ∠，且BD CD =，求证：AB AC =．

知识互联⽹

思路导航

例题精讲

题型⼀：倍长中线A

B

C

D

【例2】 ⑴如下左图，已知ABC △中，AB AC =，CE 是AB 边上的中线，延长AB 到D ，

使BD AB =．给出下列结论：①AD =2AC ；②CD =2CE ；③∠ACE =∠BCD ；④CB 平分∠DCE ，则以上结论正确的是 ．

⑵如下右图，在△ABC 中，点D 、E 为边BC 的三等分点，给出下列结论：①BD =DE =EC ；②AB +AE ＞2AD ；③AD +AC＞2AE ；④AB +AC ＞AD +AE ，则以上结论正确的是 ．

【例3】 如图，已知在ABC △中，AD 是BC 边上的中线，E 是AD 上⼀点，延长BE 交AC

于F ，AF EF =，求证：AC BE =．

【例4】 在正⽅形ABCD 中，PQ ⊥BD 于P ，M 为QD 的中点，试探究MP 与MC 的关系．A

B

PQ P

M

D

C

B

A

典题精练E

D

C

B

A

F

E D C

B A M

E

D B

E

D C

B

A

定 义

⽰例剖析

截长：即在⼀条较长的线段上截取⼀段较短的线段D

C

B

A

在线段AB 上截取AD AC =

补短：即在较短的线段上补⼀段线段使其和较长的线段相等A

B C D

延长AC ，使得AD AB =

【例5】 在ABC △中，A ∠的平分线交BC 于D ，AB AC CD =+，40B ∠=?，求C ∠的⼤

⼩．D C

B A

【例6】 如图，在ABC △中，2B C ∠=∠，BAC ∠的平分线AD 交BC 于点D ．

思路导航

例题精讲

典题精练题型⼆：截长补短

第1页（共31页）

倍长中线

知识导航

中线是三角形中的重要线段之一，在利用中线解决几何问题时，常常采用“倍长中线法”添加辅助线。

倍长中线：延长三角形中线，是得延长后的线段是原中线的2倍。目的是为构造一对8字型全等三角形（SAS），从而实现边角的转移。

知识梳理

倍长中线

AD是ABC△的中线，延长AD至E，使DEAD，连接BE.

结论：

① ACDBED△≌△

② ACBE，CADBED

③ ACBE∥

倍长类中线

ABC△中，D是BC的中点，延长ED至F，使DEDF，连接CF.

结论：

① BEDCFD△≌△

② CFBE，CFDBED

③ CFBE∥

易错点睛

倍长中线的目的在于转移边角，需要注意的是要注意延长哪一条线段或者类中线；倍长之后，需要考虑连接哪一条线段从而构造全等，实现所需的线段进行转移。

DABCEDDABCACBEF

第2页（共31页）

模块一 有关倍长中线的全等模型

【范例】

（2014秋•江汉区校级月考）如图，在ABC中，AD为中线，求证：2ABACAD．

【分析】

延长AD至E，使DEAD，构造ADCEDB，再根据三角形的三边关系可得

2ABACAD。

【解答】

证明：由BDCD，再延长AD至E，使DEAD，

D为BC的中点，

DBCD，

在ADC和EDB中ADDEADCBDEDBCD，

()ADCEDBSAS，

BEAC，

在ABE中，ABBEAE，

2ABACAD；

DABCDCBAE

第3页（共31页）

【核心考点1】倍长中线

1．（2016秋•五莲县期中）如图，ABC中，D为BC的中点．

（1）求证：2ABACAD；

（2）若5AB，3AC，求AD的取值范围．

【分析】

（1）再延长AD至E，使DEAD，构造ADCEDB，再根据三角形的三边关

初中数学全等专题倍长中线法(含答案)

得到AD+AC＞2AE，故②、③正确。由于∠BAE=∠CDE，故ABE和CDE相似，因此XXX，所以AB+AC＞AD+AE，即AB+AC＞AD+AD，即AB+AC＞2AD，故④正确。故选项D全部正确。

根据题意可知，AD+AC＞2AE，将两式相加可得到XXX＞2AD+2AE，即AB+AC＞AD+AE。因此，可以得出①②③④均正确的结论。

首先，根据题目要求，需要删除明显有问题的段落。因此，可以删除最后一段话，因为它没有任何意义。

其次，需要修正文章中的格式错误。可以将每个式子单独成行，以突出重点。同时，可以使用符号“=”、“＞”等来表示不同的关系，使文章更加清晰明了。

最后，需要对每段话进行小幅度的改写，以使其更加流畅自然。例如，可以使用更加简洁的语言，避免重复和冗长，同时保持逻辑严密。

综上所述，修正后的文章如下：

根据题意可知，有AD+AC＞2AE。将两式相加可得到XXX＞2AD+2AE，即AB+AC＞AD+AE。因此，可以得出①②③④均正确的结论。

首先，由题目可知BF∥CD。其次，根据题意，可以得出△XXX≌△XXX。因此，可以得出AB=BF。最后，由题目可知△ABE为等腰三角形。

初中几何中点问题之倍长中线

中点，顾名思义，把一条线段分为两条相等的线段的点,叫做这条线段的中点。

题型一：倍长中线

你需要的知识点：中线，三角形全等

你遇到它的时间：初一下学期至中考

你觉得难点在这：辅助线构造

你需要会的技能：加倍，加倍，加倍！

在你眼中，这类题应该长这个样子

结论：这类题型倍长中线后一般会构造出一组全等，一组平行，常用于构造全等三角形。倍长中线多用于构造全等三角形和证明边之间的关系(通常用"SAS"证明)

目的：在于进行边和角的转移，并且可以构造出两倍的线段。

注:一般都是原题已经有中线（或类中线）时用，不太会有自己画中线的时候。

题型二：倍长类中线

当然有时候题中会只出现中点，但是没有中线，这时候我们一般习惯于把这条线称之为类中线。

拓展：倍长中线之两次全等

通常，在综合题型中，倍长中线后的第一组全等只是一个基础，往往还需证明第二组全等，但是难点就在于如何去倍长中线，倍长中线后去连接什么线，这是问题的关键。这时一般需要去试错，尤其是当有两个中点时，一般是倍长中线后大概率会有另一组的全等。如下题，其实倍长CE后不管连接FA还是连接FB，这两种方法都可以继续下去。

最后，不是所有的中点问题都是可以进行倍长中线的，还有斜边中线，中位线，三线合一等多种中点问题，倍长中线只是其中一个，其余的问题我们下期再见。

全等模型-倍长中线

倍长中线

知识梳理

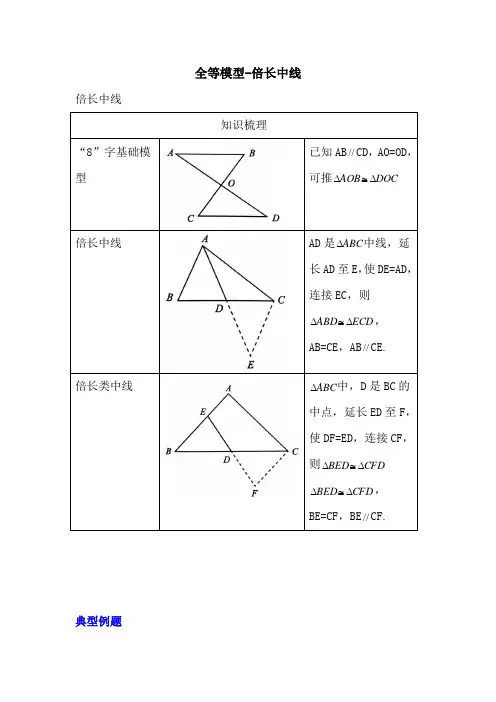
“8”字基础模型

已知AB//CD，AO=OD，可推DOCAOB

倍长中线

AD是ABC中线，延长AD至E，使DE=AD，连接EC，则ECDABD，AB=CE，AB//CE.

倍长类中线

ABC中，D是BC的中点，延长ED至F，使DF=ED，连接CF，则CFDBEDCFDBED，BE=CF，BE//CF.

典型例题 1.已知AD是ABC中BC边上的中线，若AB＝4，AC＝6，则AD的取值范围是（ ）.

A.1＞AD B.5＜AD C.51＜＜AD D.102＜＜AD

2.在△ABC和△CDE中，点A在线段CE上，B、C、D三点共线，∠BAC=∠CED，BC=CD，求证：AB=ED.

变式训练

1.在△ABC和△CDE中，点A在线段CE上，B、C、D三点共线，BC=CD，AB=ED，求证：∠BAC=∠CED.

CBDEACBDEA2.在△ABC和△CDE中，点A在线段CE上，B、C、D三点共线，∠BAC=∠CED，AB=CD，求证：BC=CD.

3.如图,在ABC中,AD是BC边上的中线,E是AD上一点,连接BE并延长交AC于点F,AF=EF,求证:AC=BE.

4.如图，AB//DC，E为BC边的中点，∠BAE=∠EAF，AF与DC的延长线相交于点F.试探究线段AB与AF，CF之间的数量关系，并证明你的结论.

CBDEA5.如图，已知ABC中，AB=AC，CE是AB边上的中线，延长AB到D，使BD=AB，求证：CD=2CE.

6.如图：CD//AB，BE=CE，DE平分∠ADC.

（1）求证：AE平分∠BAD.

（2）求证：AB+CD=AD.

能力突破

1. 已知△DEF的顶点D在△ABC的边上（不与B、C重合），且∠BAC+∠EDF=180°，AB=DF，AC=DE，点Q为EF的中点，直线DQ交直线AB于点P.

______________________________________________________________________________________________________________

精品资料 倍长中线法

知识网络详解：

中线是三角形中的重要线段之一，在利用中线解决几何问题时，常常采用“倍长中线法”添加辅助线．

所谓倍长中线法，就是将三角形的中线延长一倍，以便构造出全等三角形，从而运用全等三角形的有关知识来解决问题的方法．

倍长中线法的过程：延长某某到某点，使某某等于某某，使什么等于什么（延长的那一条），用SAS证全等（对顶角）

倍长中线最重要的一点，延长中线一倍，完成SAS全等三角形模型的构造。

【方法精讲】常用辅助线添加方法——倍长中线

△ABC中

方式1： 延长AD到E，

AD是BC边中线 使DE=AD，

连接BE

方式2：间接倍长

DABCEDABCFEDCBANDCBAM______________________________________________________________________________________________________________

精品资料

作CF⊥AD于F， 延长MD到N，

作BE⊥AD的延长线于E 使DN=MD，

连接BE 连接CN

经典例题讲解：

【压轴必刷】2023年中考数学压轴大题之经典模型培优案

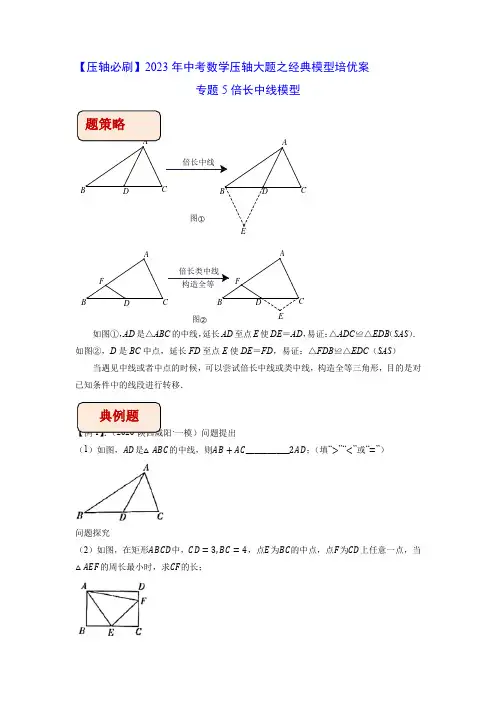
专题5倍长中线模型

如图①，AD是△ABC的中线，延长AD至点E使DE＝AD，易证：△ADC≌△EDB（SAS）．

如图②，D是BC中点，延长FD至点E使DE＝FD，易证：△FDB≌△EDC（SAS）

当遇见中线或者中点的时候，可以尝试倍长中线或类中线，构造全等三角形，目的是对已知条件中的线段进行转移．

【例1】．（2020·陕西咸阳·一模）问题提出

（1）如图，𝐴𝐷是△𝐴𝐵𝐶的中线，则𝐴𝐵+𝐴𝐶__________2𝐴𝐷；（填“>”“<”或“=”）

问题探究

（2）如图，在矩形𝐴𝐵𝐶𝐷中，𝐶𝐷=3,𝐵𝐶=4，点𝐸为𝐵𝐶的中点，点𝐹为𝐶𝐷上任意一点，当△𝐴𝐸𝐹的周长最小时，求𝐶𝐹的长；

②图①图构造全等倍长类中线倍长中线EEDCBAFFABCDABCDDCBA典例题

题策略 问题解决

（3）如图，在矩形𝐴𝐵𝐶𝐷中，𝐴𝐶=4,𝐵𝐶=2，点𝑂为对角线𝐴𝐶的中点，点𝑃为𝐴𝐵上任意一点，点𝑄为𝐴𝐶上任意一点，连接𝑃𝑂、𝑃𝑄、𝐵𝑄，是否存在这样的点𝑄，使折线𝑂𝑃𝑄𝐵的长度最小？若存在，请确定点𝑄的位置，并求出折线𝑂𝑃𝑄𝐵的最小长度；若不存在，请说明理由．

【例2】．（2021·湖北武汉·八年级期中）已知△𝐴𝐵𝐶中，

（1）如图1，点E为𝐵𝐶的中点，连𝐴𝐸并延长到点F，使𝐹𝐸=𝐸𝐴，则𝐵𝐹与𝐴𝐶的数量关系是________．

（2）如图2，若𝐴𝐵=𝐴𝐶，点E为边𝐴𝐶一点，过点C作𝐵𝐶的垂线交𝐵𝐸的延长线于点D，连接𝐴𝐷，若∠𝐷𝐴𝐶=∠𝐴𝐵𝐷，求证：𝐴𝐸=𝐸𝐶．

（3）如图3，点D在△𝐴𝐵𝐶内部，且满足𝐴𝐷=𝐵𝐶，∠𝐵𝐴𝐷=∠𝐷𝐶𝐵，点M在𝐷𝐶的延长线上，连𝐴𝑀交𝐵𝐷的延长线于点N，若点N为𝐴𝑀的中点，求证：𝐷𝑀=𝐴𝐵．

【压轴必刷】中考数学压轴大题之经典模型培优案

专题5倍长中线模型

【例1】问题提出

（1）如图，AD是ABC的中线，则ABAC__________2AD；（填“”“”或“”）

问题探究

（2）如图，在矩形ABCD中，3,4CDBC，点E为BC的中点，点F为CD上任意一点，当AEF的周长最小时，求CF的长；

问题解决

（3）如图，在矩形ABCD中，4,2ACBC，点O为对角线AC的中点，点P为AB上任意一点，点Q为AC上任意一点，连接POPQBQ、、，是否存在这样的点Q，使折线OPQB的长度最小？若存在，请确定点Q的位置，并求出折线OPQB的最小长度；若不存在，请说明理由．

【答案】（1）＞；（2）1CF；（3）当点Q与AC的中点O重合时，折线OPQB的长度最小，最小长度为4．

【分析】

（1）如图（见解析），先根据三角形全等的判定定理与性质得出ABEC，再根据三角形的三边关系定理即可得；

（2）如图（见解析），先根据矩形的性质得出3,90,//ABBBCDABCD，从而可得AE的长，再根典例题 据三角形的周长公式、两点之间线段最短得出AEF的周长最小时，点F的位置，然后利用相似三角形的判定与性质即可得；

（3）如图（见解析），先根据轴对称性质、两点之间线段最短得出折线OPQB的长度最小时，,,,BQPO四点共线，再利用直角三角形的性质、矩形的性质得出30BAC，23AB，2AO，然后利用轴对称的性质、角的和差可得23,2ABAO，90BAO，由此利用勾股定理可求出BO的长，即折线OPQB的最小长度；设BO交AC于点Q，根据等边三角形的判定与性质可得2AQ，从而可得AQAO，由此即可得折线OPQB的长度最小时，点Q的位置．

【解析】

（1）如图，延长AD，使得DEAD，连接CE

AD是ABC的中线

BDCD

1

板块 考试要求

A级要求 B级要求 C级要求

全等三角形的性质及判定 会识别全等三角形 掌握全等三角形的概念、判定和性质，会用全等三角形的性质和判定解决简单问题 会运用全等三角形的性质和判定解决有关问题

三角形中线的定义：三角形顶点和对边中点的连线

三角形中线的相关定理： 直角三角形斜边的中线等于斜边的一半

等腰三角形底边的中线三线合一(底边的中线、顶角的角平分线、底边的高重合)

三角形中位线定义：连结三角形两边中点的线段叫做三角形的中位线．

三角形中位线定理：三角形的中位线平行于第三边并且等于它的一半．

中位线判定定理：经过三角形一边中点且平行于另一边的直线必平分第三边．

中线中位线相关问题(涉及中点的问题)

见到中线(中点)，我们可以联想的内容无非是倍长中线以及中位线定理(以后还要学习中线长公式)，尤其是在涉及线段的等量关系时，倍长中线的应用更是较为常见．

知识点睛 中考要求 第二讲

全等三角形与

中点问题

2

版块一 倍长中线

【例1】 (2002年通化市中考题)在△ABC中，9,5ACAB，则BC边上的中线AD的长的取值范围是什么？

【补充】已知：ABC中，AM是中线．求证：1()2AMABAC．

MCBA

【例2】 (2008年巴中市高中阶段教育学校招生考试)已知：如图，梯形ABCD中，ADBC∥，点E是CD的中点，BE的延长线与AD的延长线相交于点F．求证：BCEFDE≌． 重点：主要掌握中线的处理方法，遇见中线考虑中线倍长法 重、难点

例题精讲

3 DFECBA

【例3】 (浙江省2008年初中毕业生学业考试(湖州市)数学试卷)如图，在ABC中，D是BC边的中点，F，E分别是AD及其延长线上的点，CFBE∥．求证：BDECDF≌．

FEDCBA

【例4】 如图，ABC中，

GFEDCBA

【例5】 如图，已知在ABC中，AD是BC边上的中线，E是AD上一点，延长BE交AC于F，AFEF，求证：ACBE．

……………………………………………………………最新资料推荐…………………………………………………

1 全等三角形问题中常见的辅助线——倍长中线法

△ABC中,AD是BC边中线

方式1：直接倍长，(图1)： 延长AD到E，使DE=AD，连接BE

方式2：间接倍长

1) （图2）作CF⊥AD于F，作BE⊥AD的延长线于E, 连接BE

2) （图3）延长MD到N，使DN=MD，连接CD

【经典例题】

例1已知，如图△ABC中，AB=5，AC=3，

则中线AD的取值范围是_________.

（提示：画出图形，倍长中线AD，利用三角形两边之和大于第三边）

例2：已知在△ABC中，AB=AC，D在AB上，E在AC的延长线上， DE交BC于F，且DF=EF.

求证：BD=CE.（提示：方法1：过D作DG∥AE交BC于G，证明ΔDGF≌ΔCEF

方法2：过E作EG∥AB交BC的延长线于G，证明ΔEFG≌ΔDFB

……………………………………………………………最新资料推荐…………………………………………………

2 方法3：过D作DG⊥BC于G，过E作EH⊥BC的延长线于H，证明ΔBDG≌ΔECH）

例3、如图，△ABC中，E、F分别在AB、AC上，DE⊥DF，D是中点，试比较BE+CF与EF的大小.

变式：如图，AD为ABC的中线，DE平分BDA交AB于E，DF平分ADC交AC于F. 求证：EFCFBE

（提示：方法1：在DA上截取DG=BD，连结EG、FG， 证明ΔBDE≌ΔGDE ΔDCF≌ΔDGF所以BE=EG、CF=FG利用三角形两边之和大于第三边

方法2：

倍长ED至H，连结CH、FH，证明FH=EF、CH=BE，利用三角形两边之和大于第三边）

_ D _ F

_ C _ B _ E _ A FECABD_ D _ F

_ C _ B _ E _ A ……………………………………………………………最新资料推荐…………………………………………………

完整版)倍长中线法(经典例题)

倍长中线法是解决几何问题中常用的方法之一。在利用中线解决问题时，我们可以通过添加辅助线，采用倍长中线法来构造全等三角形，从而运用全等三角形的知识来解决问题。

具体来说，倍长中线法的过程是：延长某一中线一倍，使其构造出全等三角形，然后利用全等三角形的有关知识来解决问题。在构造全等三角形时，我们可以采用两种常用的方法：一是将中线延长到某一点，使其等于另一条中线，然后利用对顶角的SAS证明全等；二是通过间接倍长的方法，利用垂线和平行线构造出全等三角形。

倍长中线法最重要的一点是延长中线一倍，完成SAS全等三角形模型的构造。我们可以通过经典例题来练这种方法，例如求中线的取值范围、证明BD等于CE、证明AF等于EF等问题。

自检自测题也是巩固这种方法的好办法。例如证明AD平分∠BAE、探究线段AB与AF、CF之间的数量关系、证明BE+CF>EF等问题都可以通过倍长中线法来解决。

专题01 全等模型--倍长中线与截长补短

全等三角形在中考数学几何模块中占据着重要地位，也是学生必须掌握的一块内容，本专题就全等三角形中的重要模型（倍长中线模型、截长补短模型）进行梳理及对应试题分析，方便掌握。

模型1.倍长中线模型

【模型解读】中线是三角形中的重要线段之一，在利用中线解决几何问题时，常常采用“倍长中线法”添加辅助线．所谓倍长中线法，就是将三角形的中线延长一倍，以便构造出全等三角形，从而运用全等三角形的有关知识来解决问题的方法．（注：一般都是原题已经有中线时用，不太会有自己画中线的时候）。

【常见模型及证法】

1、基本型：如图1，在三角形ABC中，AD为BC边上的中线.

证明思路：延长AD至点E，使得AD=DE. 若连结BE，则BDECDA；若连结EC，则ABDECD；

2、中点型:如图2，C为AB的中点.

证明思路：若延长EC至点F，使得CFEC，连结AF，则BCEACF;

若延长DC至点G，使得CGDC，连结BG，则ACDBCG.

3、中点+平行线型：如图3, //ABCD，点E为线段AD的中点.

证明思路：延长CE交AB于点F (或交BA延长线于点F)，则EDCEAF.

1．（2022·山东烟台·一模）（1）方法呈现：

如图①：在ABC中，若6AB，4AC，点D为BC边的中点，求BC边上的中线AD的取值范围．

解决此问题可以用如下方法：延长AD到点E使DEAD，再连接BE，可证ACDEBD△≌△，从而把AB、AC，2AD集中在ABE△中，利用三角形三边的关系即可判断中线AD的取值范围是_______________，这种解决问题的方法我们称为倍长中线法；

（2）探究应用：如图②，在ABC中，点D是BC的中点，DEDF于点D，DE交AB于点E，DF交AC于点F，连接EF，判断BECF与EF的大小关系并证明；

（3）问题拓展：如图③，在四边形ABCD中，//ABCD，AF与DC的延长线交于点F、点E是BC的中点，若AE是BAF的角平分线．试探究线段AB，AF，CF之间的数量关系，并加以证明．

(完满版)倍长中线法(经典例题)

倍长中线法

知识网络详解：

中线是三角形中的重要线段之一， 在利用中线解决几何问题时， 常常采用 “倍长中线法 ” 增加辅助线．

所谓倍长中线法， 就是将三角形的中线延长一倍， 以便构造出全等三角形， 从而运用全等三角形的有关知识来解决问题的方法．

倍长中线法的过程： 延长某某到某点，使某某等于某某， 使什么等于什么（延长的那一条），用 SAS证全等（对顶角）

倍长中线最重要的一点，延长中线一倍，完成 SAS全等三角形模型的构造。 【方法精讲 】常用辅助线增加方法——倍长中线

A

A

B C D

△ ABC中 方式 1： 延长 AD 到 E，

AD 是 BC 边中线 使 DE=AD， B C 连接 BE D

方式 2：间接倍长

A

F

B D C

E

E

A

作 CF⊥ AD于 F， M 延长 MD到

N，

D 作 BE⊥ AD的延长线于 E B 使 DN=MD， C

连接 BE N 连接 CN

经典例题讲解：

例 1：△ ABC中， AB=5， AC=3，求中线 AD 的取值范围 (完满版)倍长中线法(经典例题)

例 2：已知在△ ABC 中， AB=AC，D 在 AB 上， E在 AC的延长线上， DE 交 BC 于 F，且

DF=EF，求证： BD=CE

A

D

B

F

C

E

例 3：已知在△ ABC 中， AD 是 BC 边上的中线， E 是 AD 上一点，且 BE=AC，延长 BE 交 AC

于 F，求证： AF=EF

A

F E

B D C

例 4：已知：如图，在 ABC 中， AB AC ， D、E 在 BC上，且 DE=EC，过 D作 DF // BA

交 AE于点 F， DF=AC. A

求证： AE 均分 BAC

、倍长中线（线段）造全等典例讲解

倍长中线法

例：ABC中，人。是・BAC的平分线，且BD=CD，求证AB=AC

E

方式1涎长AD到E,

使DE=AD，连接BE

【经典例题】 例1：已知在△ ABC中，AB=AC，。在AB上，E在AC的延长线上，DE交BC于F,且

A

DF=EF，求证：BD=CE 人 【方法精讲】常用辅助线添加方法一一倍长中线

AD是BC边中线 D

及时练习1 : ZXABC中，AB=5 , AC=3，求中线AD的取值范围

例3：如图AD为ABC的中线DE平分・BDA交AB于E，DF平分・ADC交AC于

F.求证：BE CF EF 例2：已知在△ ABC中，AD是BC边上的中线, E是AD ± 一点，且 BE二AC,延长BE

及时练习2、已知：如图，在ABC中，作 AB式AC，D、E在BC上，且DE=EC过D DF //

BA 交 AE 于点 F，DF=AC.

课后作业

1.（ “希望杯”试题）已知'如图△ ABC中，AB=10AC=8贝忡线AD的取值范围是方式2 :间接倍长（不一定是中线，以中点为端点的线段即可）

作CF丄AD于F,

作BE丄AD的延长线于E

连接BE 延长MD到N,

使 DN=MD

连接CD

求证：AE平分・BAC A 2：如图， △ ABC中,E、F分别在AB AC±^Z®LDF, D是中点，试比较BE+CF与EF

过矢训练

1：如图， △ ABC中，BD=DC=ACE是DC的中点，求证：AD平分Z BAE.

例 5：已知 CD=AB , ZBDA= /BAD, AE 是 AABD 的中线，求证:Z C= ZBAE的大小. 2. （ 09崇文二模）以ABC的两边AB AC为腰分别向外作等腰Rt砂和等腰Rt

,・BAD二CAE =90旌接DE, M、N分别是BC DE的中点•探究：AM

ABC

与DE的位置矢系及数量矢系.（1）如图①当 为直角三角形时，AM与DE的位置矢