全等模型-倍长中线与截长补短模型(解析版)

1

一、手拉手模型

要点一：手拉手模型

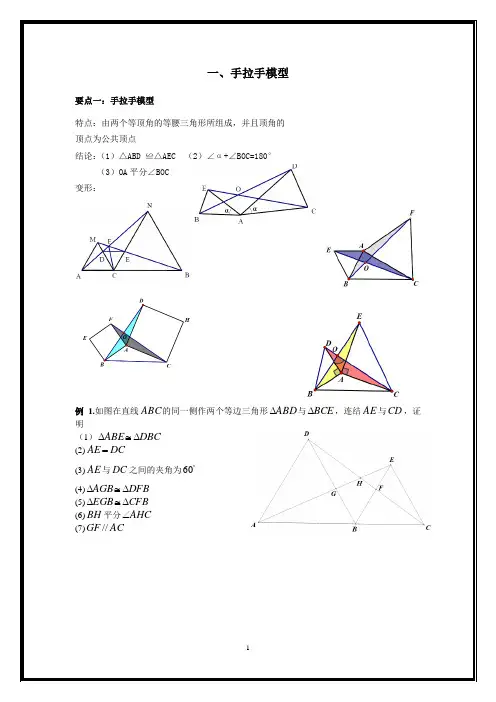
特点：由两个等顶角的等腰三角形所组成，并且顶角的

顶点为公共顶点

结论：（1）△ABD ≌△AEC （2）∠α+∠BOC=180°

（3）OA平分∠BOC

变形：

例1.如图在直线ABC的同一侧作两个等边三角形ABD与BCE，连结AE与CD，证明

（1）DBCABE

(2)DCAE

(3)AE与DC之间的夹角为60

(4)DFBAGB

(5)CFBEGB

(6)BH平分AHC

(7)ACGF//

2

变式精练1：如图两个等边三角形ABD与BCE，连结AE与CD，

证明（1）DBCABE

（2）DCAE

（3）AE与DC之间的夹角为60

（4）AE与DC的交点设为H,BH平分AHC

变式精练2：如图两个等边三角形ABD与BCE，连结AE与CD，

证明（1）DBCABE

(2）DCAE

(3）AE与DC之间的夹角为60

(4）AE与DC的交点设为H,BH平分AHC

例2：如图，两个正方形ABCD与DEFG,连结CEAG,,二者相交于点H

问：（1）CDEADG是否成立？

（2）AG是否与CE相等？

（3）AG与CE之间的夹角为多少度？

（4）HD是否平分AHE？

例3：如图两个等腰直角三角形ADC与EDG，连结CEAG,,二者相交于点H

问：（1）CDEADG是否成立？

（2）AG是否与CE相等？

（3）AG与CE之间的夹角为多少度？

（4）HD是否平分AHE？

3

例4：两个等腰三角形ABD与BCE，其中BDAB,,EBCBCBEABD,连结AE与CD，

问：（1）DBCABE是否成立？

（2）AE是否与CD相等？

（3）AE与CD之间的夹角为多少度？

（4）HB是否平分AHC？

二、倍长与中点有关的线段

倍长中线类

☞考点说明：凡是出现中线或类似中线的线段，都可以考虑倍长中线，倍长中线的目的是可以旋转等长度的线段，从而达到将条件进行转化的目的。

第四章.全等三角形

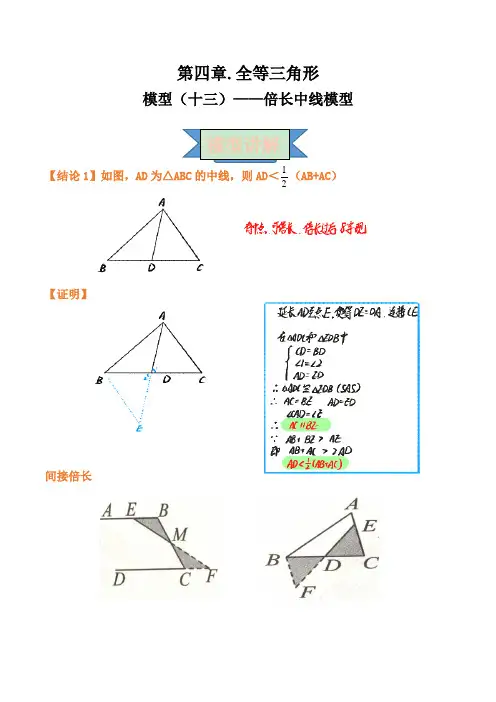
模型（十三）——倍长中线模型

【结论1】如图，AD为△ABC的中线，则AD＜21（AB+AC）

【证明】

间接倍长

模型讲解

典例1 ☆☆☆☆☆

如图，△ABC中，若 AB=8，AC=6，则 BC边上的中线AD长度的取值范围为（ ）.

A.6＜AD＜8 B.6≤AD≤8 C.1＜AD＜7 D.1≤AD≤7

【答案】C

【解析】如图，延长AD至点E，使ED=AD，连接 BE，

∵AD是 BC边上的中线，∴由倍长中线模型可知 BE= AC.

∵AB-BE＜AE＜AB+BE, ∴AB-AC＜AE＜AB+AC.

∵AB=8,AC=6, ∴8-6＜AE＜8＋6,

∴2＜AE＜14.

∵AD=ED,∴AE=AD+ED=AD+AD=2AD,

即 2＜2AD＜14， 典例秒杀 ∴1＜AD＜7. 故选 C

典例2 ☆☆☆☆☆

如图，AD是△ABC的中线，E，F分别在边AB，AC上（E，F不与端点重合），且

DE⊥DF，则（ )

A .BE+CF＞EF B.BE＋CF=EF

C. BE＋CF＜EF D.BE＋CF 与EF 的长短关系不确定

【答案】A

【解析】如图，延长 ED 至点G，使 DG=ED，连接 CG，FG.

∵AD是BC 边上的中线，由倍长中线的拓展模型可得 CG= BE.

又∵DE⊥DF，DG=ED， ∴FD 是 EG 的垂直平分线， ∴FG=EF.

∵GC+CF＞FG,∴BE+CF>EF. 故选 A.

典例3 ☆☆☆☆☆ 如图所示，E 是 BC 的中点，∠BAE= ∠CDE.若 AB=6，则CD= ( ).

A .6 B.3 C.12 D. 无法确定

初中数学三角形全等—倍长中线法模型专题分类练习大全

基础模型: △ABC 中, AD 是 BC 边中线

A

B C D思路 1： 延长 AD 到 E，使 DE=AD，连接 BE

A

BC D

E思路 2：间接倍长,延长 MD 到 N，使 DN=MD，连接 CN

A

M

BDC

N

思路 3, 作 CF⊥AD 于 F，作 BE⊥AD 的延长线于 E

A

F

B DC

E

1．如图，在△ABC 中，AC=5，中线 AD=7，则 AB 边的取值范围是（）

A．1＜AB＜29B．4＜AB＜24 C．5＜AB＜19 D．9＜AB＜19

2．如图，△ABC 中，AB=AC，点 D 在 AB 上，点 E 在 AC 的延长线上，DE 交 BC 于 F，且 DF=EF，求证：BD=CE．

3．如图，在△ABC 中，AD 为中线，求证：AB+AC＞2AD．

4．小明遇到这样一个问题，如图 1，△ABC 中，AB=7，AC=5，点 D 为 BC 的中点，求 AD 的取 值范围．

小明发现老师讲过的“倍长中线法”可以解决这个问题，所谓倍长中线法，就是将三角形的中线

延长一倍，以便构造出全等三角形，从而运用全等三角形的有关知识来解决问题的方法，他的

做法是：如图 2，延长 AD 到 E，使 DE=AD，连接 BE，构造△BED≌△CAD，经过推理和计算使

问题得到解决．

请回答：（1）小明证明△BED≌△CAD 用到的判定定理是： （用字母表示）

（2）AD 的取值范围是

小明还发现：倍长中线法最重要的一点就是延长中线一倍，完成全等三角形模型的构造．

参考小明思考问题的方法，解决问题：

如图 3，在正方形 ABCD 中，E 为 AB 边的中点，G、F 分别为 AD，BC 边上的点，若 AG=2，BF=4，

∠GEF=90°，求 GF 的长．

5．已知：在△ABC 中，AD 是 BC 边上的中线，E 是 AD 上一点，且 BE=AC，延长 BE 交 AC 于 F， 求证：AF=EF．

1 / 5

初一（下）数学暑假班全等模型课第2讲

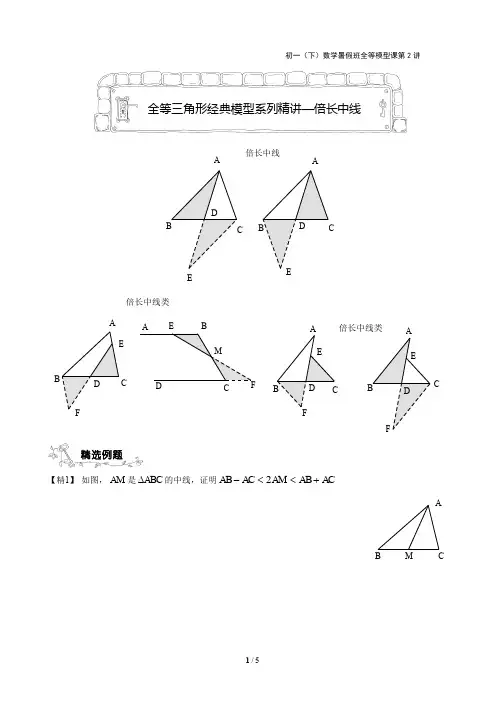
【精1】 如图，AM

是ABC

的中线，证明2ABACAMABAC

倍长中线

A

BCD

E

ED

CBA

倍长中线类

M

FE

D

CB

A

FE

DCBA

倍长中线类

A

BC

DE

FFE

D

CBA

MC

BA全等三角形经典模型系列精讲—倍长中线

精选例题

2 / 5

初一（下）数学暑假班全等模型课第2讲

【精2】 已知

ABC,

ACAB，

AM是中线：求证：11

22ACABAMABAC

【精3】 已知在ABC

中，AD

是BC

边上的中线，E

是AD

上一点，且BEAC

，延长BE

交AC

于F

，

求证：AFEF

【精4】 求证：如果两个三角形有两条边和第三边上的中线对应相等，那么这两个三角形全等

翻译：如图，ABC

和DEF

中，ABDE

，ACDF

，AMDN

，

求证：ABC

≌DEF

M

CBA

F

E

DC

BA

D

EFNMC

BA

3 / 5

初一（下）数学暑假班全等模型课第2讲

【精5】 如图，ABC△中，90A,

D为斜边为BC中点，

E、

F分别为

AB、AC上的点，且

DEDF，

若3BE，4CF，试求

EF的长

【精6】 如图，CB、CD分别是钝角AEC和锐角ABC的中线，且ACAB，求证：2CECD

【精7】 如图，在ABC

外，作等腰直角ABD

和等腰直角ACE

，连接DE

，取DE

中点，连接AF

，证明：1

2BCAF

,AFBC

FE

D

CBA

E

DC

BA

F

ED

C

BA

4 / 5

初一（下）数学暑假班全等模型课第2讲

【精8】 已知，如图，在ABC中，ABAC，

D、

E在BC上，且DEEC，过

D作

DF∥

BA交

AE于

点

F，DFAC.

求证：

AE平分BAC

【精9】 如图，已知AD

是ABC

的中线，AEAB

，AFAC

，且AEAB

，AFAC

， 求证：1

2ADEF

F

EDC

BA

FEDC

BA

5 / 5

初一（下）数学暑假班全等模型课第2讲

全等三角形中重要几何模型专题讲解

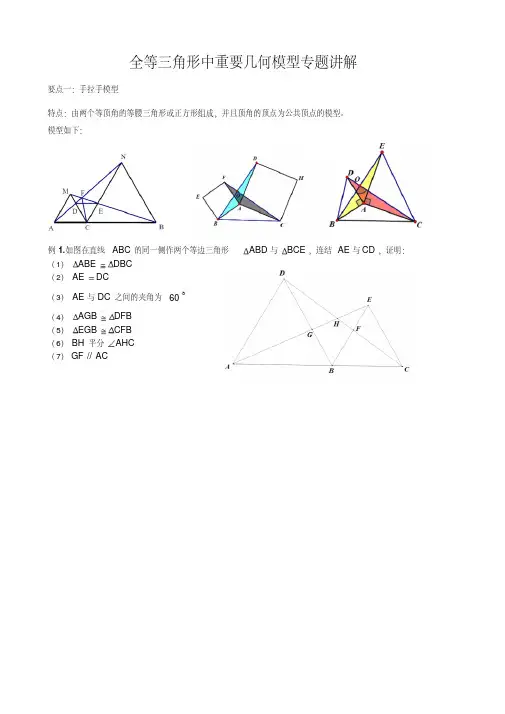
要点一：手拉手模型

特点：由两个等顶角的等腰三角形或正方形组成，并且顶角的顶点为公共顶点的模型。

模型如下：

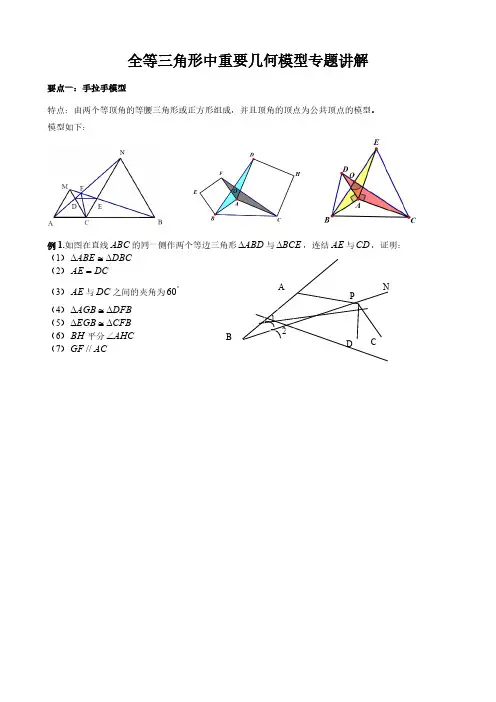
例1.如图在直线ABC

的同一侧作两个等边三角形ABD

与BCE

，连结AE

与CD

，证明：

（1）DBCABE

（2）DCAE

（3）AE

与DC

之间的夹角为60

（4）DFBAGB

（5）CFBEGB

（6）BH

平分AHC

（7）ACGF//

全等三角形中重要几何模型专题讲解

要点一：手拉手模型

特点：由两个等顶角的等腰三角形或正方形组成，并且顶角的顶点为公共顶点的模型。

模型如下：

例1.如图在直线的同一侧作两个等边三角形与，连结与，证明：ABCABDBCEAECD

（1）DBCABE

（2）DCAE

（3）与之间的夹角为AEDC60

（4）DFBAGB

（5）CFBEGB

（6）平分BHAHC

（7）ACGF//N

DCBA

P

21

变式精练1：如图两个等边三角形与，连结与ABDBCEAE

，CD

证明（1）DBCABE

（2）DCAE

（3）与之间的夹角为AEDC60

（4）与的交点设为,平分AEDCHBHAHC

变式精练2：如图两个等边三角形与，连结与ABDBCEAE

，CD

证明（1）DBCABE

(2）DCAE

(3）与之间的夹角为AEDC60

(4）与的交点设为,平分AEDCHBHAHC

N

例2：如图，两个正方形与,连结ABCDDEFG

,二者相交于点CEAG,H

问：（1）是否成立？CDEADG

（2）是否与相等？AGCE

（3）与之间的夹角为多少度？AGCE

（4）是否平分？HDAHE

例3：如图两个等腰直角三角形与，连结,二者相交于点ADCEDGCEAG,H

问：（1）是否成立？CDEADG

（2）是否与相等？AGCE

（3）与之间的夹角为多少度？AGCE

（4）是否平分？HDAHE

D

例4：两个等腰三角形与，其中,,连结与ABDBCEBDAB,EBCBCBEABDAE

，CD

问：（1）是否成立？DBCABE

（2）是否与相等？AECD

（3）与之间的夹角为多少度？AECD

（4）是否平分？HBAHC

C

要点二：截长补短法

若遇到证明线段的和差倍分关系时，通常考虑截长补短法，构造全等三角形。

1、截长法：在较长线段中截取一段等于另两条中的一条，然后证明剩下部分等于另一条；

2、补短法：将一条较短线段延长，延长部分等于另一条较短线段，然后证明新线段等于较长线

第 1 页 共 12 页 A全等三角形之手拉手模型倍长中线截长补短法

≌△AEC （2）∠α+∠BOC=180 （3）OA平分∠BOC变形：

例

1、如图在直线的同一侧作两个等边三角形与，连结与，证明（1）(2)(3)

与之间的夹角为(4)(5)(6)

平分(7)变式精练1：如图两个等边三角形与，连结与，证明（1）（2）（3） 与之间的夹角为（4） 与的交点设为,平分变式精练2：如图两个等边三角形与，连结与，证明（1）(2）(3） 与之间的夹角为(4） 与的交点设为,平分例2：如图，两个正方形与,连结,二者相交于点问：（1）是否成立？（2） 是否与相等？（3） 与之间的夹角为多少度？（4） 是否平分？例3：如图两个等腰直角三角形与，连结,二者相交于点问：（1）是否成立？（2）是否与相等？（3）与之间的夹角为多少度？（4）是否平分？例4：两个等腰三角形与，其中,,连结与，问：（1）是否成立？（2）是否与相等？（3）与之间的夹角为多少度？（4）是否平分？例5：如图，点

A、

B、C在同一条直线上，分别以A 第 2 页 共 12 页 B、BC为边在直线AC的同侧作等边三角形△AB

D、△BCE、连接AE、DC，AE与DC所在直线相交于F，连接F

B、判断线段F

B、FE与FC之间的数量关系，并证明你的结论。

【练1】

如图，三角形ABC和三角形CDE都是等边三角形，点A,E,D,同在一条直线上，且角EBD=62，求角AEB的度数 倍长与中点有关的线段倍长中线类☞考点说明：凡是出现中线或类似中线的线段，都可以考虑倍长中线，倍长中线的目的是可以旋转等长度的线段，从而达到将条件进行转化的目的：将题中已知和未知条件集中在一对三角形中、构造全等三角形、平移线段。

【方法精讲】

常用辅助线添加方法倍长中线 △ABC中 方式1：

延长AD到E， AD是BC边中线 使DE=AD， 连接BE 方式2：间接倍长 作CF⊥AD于F， 延长MD到N， 作BE⊥AD的延长线于E 使DN=MD，连接BE 连接CD

三角形全等之手拉手模型倍长中线截长补短法旋转寻找三角形全等方法归纳总结

SANY标准化小组 #QS8QHH-HHGX8Q8-GNHHJ8-HHMHGN#

一、手拉手模型

要点一：手拉手模型

特点：由两个等顶角的等腰三角形所组成，并且顶角的

顶点为公共顶点

结论：（1）△ABD ≌△AEC （2）∠α+∠BOC=180°

（3）OA平分∠BOC

变形：

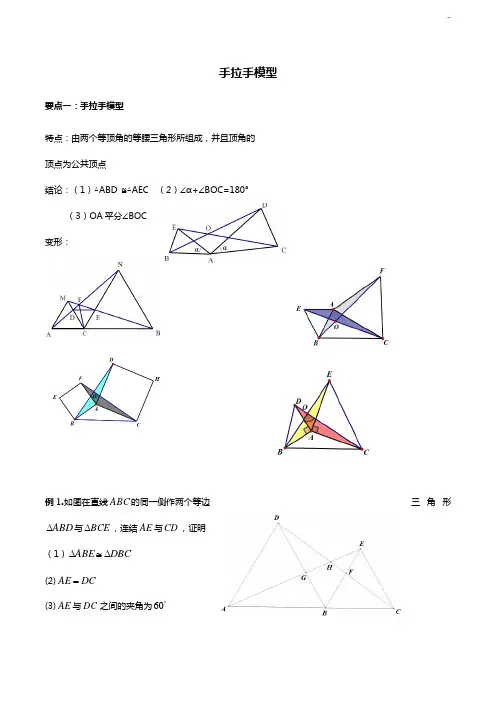
例1.如图在直线ABC的同一侧作两个等边三角形ABD与BCE，连结AE与CD，证明

（1）DBCABE

(2)DCAE

(3)AE与DC之间的夹角为60

(4)DFBAGB

(5)CFBEGB

(6)BH平分AHC

(7)ACGF//

变式精练1：如图两个等边三角形ABD与BCE，连结AE与CD，

证明（1）DBCABE

（2）DCAE

（3）AE与DC之间的夹角为60

（4）AE与DC的交点设为H,BH平分AHC

变式精练2：如图两个等边三角形ABD与BCE，连结AE与CD，

证明（1）DBCABE

(2）DCAE

(3）AE与DC之间的夹角为60

(4）AE与DC的交点设为H,BH平分AHC

例2：如图，两个正方形ABCD与DEFG,连结CEAG,,二者相交于点H

问：（1）CDEADG是否成立

（2）AG是否与CE相等

（3）AG与CE之间的夹角为多少度

（4）HD是否平分AHE

例3：如图两个等腰直角三角形ADC与EDG，连结CEAG,,二者相交于点H

问：（1）CDEADG是否成立

（2）AG是否与CE相等

（3）AG与CE之间的夹角为多少度

（4）HD是否平分AHE

例4：两个等腰三角形ABD与BCE，其中BDAB,,EBCBCBEABD,连结AE与CD，

,.

手拉手模型

要点一：手拉手模型

特点：由两个等顶角的等腰三角形所组成，并且顶角的

顶点为公共顶点

结论：（1）△ABD ≌△AEC （2）∠α+∠BOC=180°

（3）OA平分∠BOC

变形：

例1.如图在直线ABC的同一侧作两个等边三角形ABD与BCE，连结AE与CD，证明

（1）DBCABE

(2)DCAE

(3)AE与DC之间的夹角为60 ,.

(4)DFBAGB

(5)CFBEGB

(6)BH平分AHC

(7)ACGF//

变式精练1：如图两个等边三角形ABD与BCE，连结AE与CD，

证明（1）DBCABE

（2）DCAE

（3）AE与DC之间的夹角为60

（4）AE与DC的交点设为H,BH平分AHC

,.

变式精练2：如图两个等边三角形ABD与BCE，连结AE与CD，

证明（1）DBCABE

(2）DCAE

(3）AE与DC之间的夹角为60

(4）AE与DC的交点设为H,BH平分AHC

,.

例2：如图，两个正方形ABCD与DEFG,连结CEAG,,二者相交于点H

问：（1）CDEADG是否成立？

（2）AG是否与CE相等？

（3）AG与CE之间的夹角为多少度？

（4）HD是否平分AHE？

,.

例3：如图两个等腰直角三角形ADC与EDG，连结CEAG,,二者相交于点H

问：（1）CDEADG是否成立？

（2）AG是否与CE相等？

（3）AG与CE之间的夹角为多少度？

（4）HD是否平分AHE？

,.

例4：两个等腰三角形ABD与BCE，其中BDAB,,EBCBCBEABD,连结AE与CD，

问：（1）DBCABE是否成立？

（2）AE是否与CD相等？

（3）AE与CD之间的夹角为多少度？

（4）HB是否平分AHC？

,.

例5：如图，点A. B. C在同一条直线上，分别以AB、BC为边在直线AC的同侧作等边三角形△ABD、△BCE.连接AE、DC，AE与DC所在直线相交于F，连接FB.判断线段FB、FE与FC之间的数量关系，并证明你的结论。

1 倍长中线专题

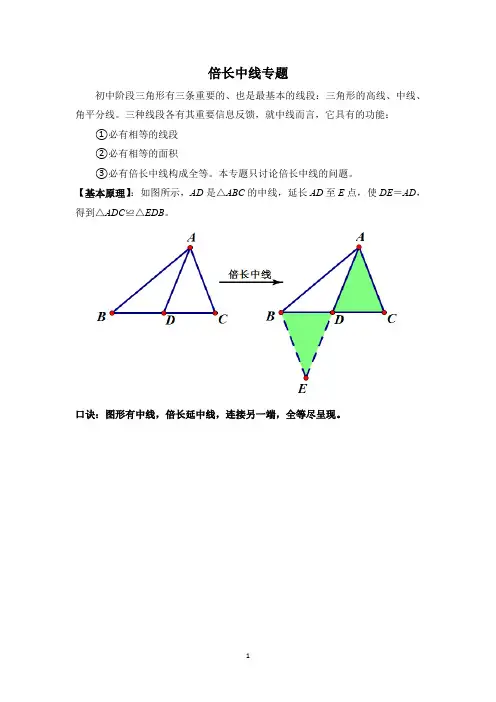
初中阶段三角形有三条重要的、也是最基本的线段：三角形的高线、中线、角平分线。三种线段各有其重要信息反馈，就中线而言，它具有的功能：

①必有相等的线段

②必有相等的面积

③必有倍长中线构成全等。本专题只讨论倍长中线的问题。

【基本原理】：如图所示，AD是△ABC的中线，延长AD至E点，使DE＝AD，得到△ADC≌△EDB。

口诀：图形有中线，倍长延中线，连接另一端，全等尽呈现。

2 【模型实例】：如图，在△ABC中，AD是BC边的中线，E是AD上一点，连接BE并延长交AC于F点，AF=EF，求证：AC=BE

证明： 如图所示。延长AD至G点，使DG=AD，连接BG。

在△ADC与△GDB中，CDBDGDBADCGDAD

∴△ADC≌△GDB

∴BG=AC，∠1=∠G

又因为AF=EF

∴∠1=∠2=∠3

∴∠3=∠G

∴BG=BE（等角对等边）

∴AC=BE

②证全等

①作倍长中线

③列出需要用的结果

④转化替代

⑤得出结果 3 【练习1】 ：如图，在在△ABC中，D为BC的中点，求证：ADACAB2

【练习2】 ：如图，在△ABC中，D为BC的中点,且AD是角平分线。

求证：AB=AC

4 【练习3】 ：AD是△ABC的中线，分别以AB边、AC边为直角边向外作等腰直角三角形，求证：EF=2AD

【练习4】 ：在四边形ABCD中，AB∥DC，E为BC边的中点，∠BAE=∠EAF，AF与DC的延长线相交于F点。试探究线段AB与AF、CF之间的数量关系，并证明你的结论。

5 截长补短专题

要证明两条线段之和等于第三条线段，可以采用“截长补短”法。

①截长法：把较长的线段截取一段等于两较短线中的一条；

②补短法：把两条较短的线段补成一条，再证与长线段相等。

【模型实例】：如图，△ABC中，∠1=∠2，∠B=2∠C。求证：AC=AB+BD

手拉手模型

要点一：手拉手模型

特点：由两个等顶角的等腰三角形所组成,并且顶角的

顶点为公共顶点

结论：1△ABD ≌△AEC 2∠α+∠BOC=180°

3OA平分∠BOC

变形：

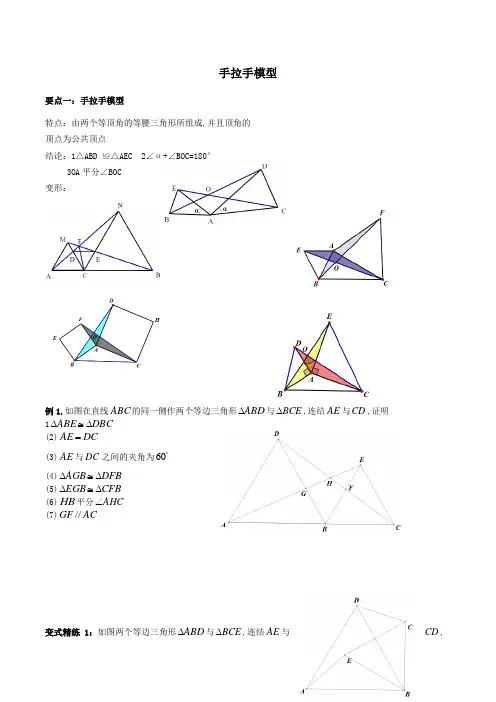
例1.如图在直线ABC的同一侧作两个等边三角形ABD与BCE,连结AE与CD,证明

1DBCABE

(2)DCAE

(3)AE与DC之间的夹角为60

(4)DFBAGB

(5)CFBEGB

(6)HB平分AHC

(7)ACGF//

变式精练1：如图两个等边三角形ABD与BCE,连结AE与CD, 证明1DBCABE

（2）DCAE

（3）AE与DC之间的夹角为60

（4）AE与DC的交点设为H,BH平分AHC

变式精练2：如图两个等边三角形ABD与BCE,连结AE与CD,

证明1DBCABE

(2）DCAE

(3）AE与DC之间的夹角为60

(4）AE与DC的交点设为H,HB平分AHC

例2：如图,两个正方形ABCD与DEFG,连结CEAG,,二者相交于点H 问：1CDEADG是否成立

（2）AG是否与CE相等

（3）AG与CE之间的夹角为多少度

（4）HD是否平分AHE

例3：如图两个等腰直角三角形ADC与EDG,连结CEAG,,二者相交于点H

问：1CDEADG是否成立

2AG是否与CE相等

3AG与CE之间的夹角为多少度

4HD是否平分AHE

例4：两个等腰三角形ABD与BCE,其中BDAB,,EBCBCBEABD,连结AE与CD, 问：1DBCABE是否成立

2AE是否与CD相等

3AE与CD之间的夹角为多少度

4HB是否平分AHC

例5：如图,点A. B. C在同一条直线上,分别以AB、BC为边在直线AC的同侧作等边三角形△ABD、△BCE.连接AE、DC,AE与DC所在直线相交于F,连接FB.判断线段FB、FE与FC之间的数量关系,并证明你的结论;

.. 一、手拉手模型

要点一：手拉手模型

特点：由两个等顶角的等腰三角形所组成，并且顶角的

顶点为公共顶点

结论：（1）△ABD ≌△AEC （2）∠α+∠BOC=180°

（3）OA平分∠BOC

变形：

例1.如图在直线ABC的同一侧作两个等边三角形ABD与BCE，连结AE与CD，证明

（1）DBCABE

(2)DCAE

(3)AE与DC之间的夹角为60

(4)DFBAGB

(5)CFBEGB

(6)BH平分AHC

(7)ACGF//

..

变式精练1：如图两个等边三角形ABD与BCE，连结AE与CD，

证明（1）DBCABE

（2）DCAE

（3）AE与DC之间的夹角为60

（4）AE与DC的交点设为H,BH平分AHC

变式精练2：如图两个等边三角形ABD与BCE，连结AE与CD，

证明（1）DBCABE

(2）DCAE

(3）AE与DC之间的夹角为60

(4）AE与DC的交点设为H,BH平分AHC

例2：如图，两个正方形ABCD与DEFG,连结CEAG,,二者相交于点H

问：（1）CDEADG是否成立？

（2）AG是否与CE相等？

（3）AG与CE之间的夹角为多少度？

（4）HD是否平分AHE？

例3：如图两个等腰直角三角形ADC与EDG，连结CEAG,,二者相交于点H

问：（1）CDEADG是否成立？

（2）AG是否与CE相等？

（3）AG与CE之间的夹角为多少度？

（4）HD是否平分AHE？

.. 例4：两个等腰三角形ABD与BCE，其中BDAB,,EBCBCBEABD,连结AE与CD，

问：（1）DBCABE是否成立？

（2）AE是否与CD相等？

（3）AE与CD之间的夹角为多少度？

（4）HB是否平分AHC？

二、倍长与中点有关的线段

倍长中线类

☞考点说明：凡是出现中线或类似中线的线段，都可以考虑倍长中线，倍长中线的目的是可以旋转等长度的线段，从而达到将条件进行转化的目的。

全等三角形辅助线之截长补短与倍长中线

一．填空题（共1小题）

1．（2015秋?宿迁校级月考）如图，在Rt△ABC中，∠C=90°，AD平分∠BAC交BC于D．若BD：DC=3：2，点D到AB的距离为6，则BC的长是 ．

二．解答题（共10小题）

2．（2010秋?涵江区期末）如图所示，在Rt△ABC中，∠C=90°，BC=AC，AD平分∠BAC交BC于D，求证：AB=AC+CD．

3．如图，AD是△ABC中BC边上的中线，求证：AD＜（AB+AC）．

4．（2013秋?藁城市校级期末）在△ABC中，∠ACB=90°，AC=BC，直线，MN经过点C，且AD⊥MN于点D，BE⊥MN于点E．

（1）当直线MN绕点C旋转到如图1的位置时，求证：DE=AD+BE；

（2）当直线MN绕点C旋转到如图2的位置时，求证：DE=AD﹣BE；

（3）当直线MN绕点C旋转到如图3的位置时，线段DE、AD、BE之间又有什么样的数量关系请你直接写出这个数量关系，不要证明．

5．已知△ABC中，∠A=60°，BD，CE分别平分∠ABC和∠ACB，BD、CE交于点O，试判断BE，CD，BC的数量关系，并说明理由．

6．（2012秋?西城区校级期中）已知：如图，△ABC中，点D，E分别在AB，AC边上，F是CD中点，连BF交AC于点E，∠ABE+∠CEB=180°，判断BD与CE的数量关系，并证明你的结论．

7．（2010秋?丰台区期末）已知：如图，在等腰直角三角形ABC中，∠ACB=90°，AC=BC，点D是△ABC内的一点，且AD=AC，若∠DAC=30°，试探究BD与CD的数量关系并加以证明．

8．已知点M是等边△ABD中边AB上任意一点（不与A、B重合），作∠DMN=60°，交∠DBA外角平分线于点N．

（1）求证：DM=MN；

（2）若点M在AB的延长线上，其余条件不变，结论“DM=MN”是否依然成立请你画出图形并证明你的结论．

1

一、手拉手模型

要点一:手拉手模型

特点：由两个等顶角的等腰三角形所组成，并且顶角的

顶点为公共顶点

结论:（1)△ABD ≌△AEC （2）∠α+∠BOC=180°

（3）OA平分∠BOC

变形:

例1。如图在直线ABC的同一侧作两个等边三角形ABD与BCE，连结AE与CD,证明

（1）DBCABE

(2)DCAE

(3)AE与DC之间的夹角为60

(4)DFBAGB

(5)CFBEGB

(6)BH平分AHC

(7)ACGF//

2

变式精练1：如图两个等边三角形ABD与BCE，连结AE与CD，

证明（1)DBCABE

（2）DCAE

（3）AE与DC之间的夹角为60

（4）AE与DC的交点设为H，BH平分AHC

变式精练2：如图两个等边三角形ABD与BCE,连结AE与CD，

证明（1）DBCABE

(2）DCAE

(3）AE与DC之间的夹角为60

(4）AE与DC的交点设为H,BH平分AHC

例2：如图，两个正方形ABCD与DEFG,连结CEAG,,二者相交于点H

问：（1）CDEADG是否成立？

（2）AG是否与CE相等？

（3）AG与CE之间的夹角为多少度？

（4）HD是否平分AHE？

例3：如图两个等腰直角三角形ADC与EDG,连结CEAG,,二者相交于点H

问：（1）CDEADG是否成立?

（2）AG是否与CE相等?

（3）AG与CE之间的夹角为多少度？

(4）HD是否平分AHE？

3

例4：两个等腰三角形ABD与BCE，其中BDAB,,EBCBCBEABD,连结AE与CD,

问：(1）DBCABE是否成立?

（2)AE是否与CD相等？

（3）AE与CD之间的夹角为多少度?

（4)HB是否平分AHC?

二、倍长与中点有关的线段

倍长中线类

☞考点说明：凡是出现中线或类似中线的线段，都可以考虑倍长中线，倍长中线的目的是可以旋转等长度的线段,从而达到将条件进行转化的目的。

王老师的课堂

1

证明举例教案（提高）

1) 等变换中的“旋转”．

2) 遇到角平分线，可以自角平分线上的某一点向角的两边作垂线，利用的思维模式是三角形全等变换中的“对折”，所考知识点常常是角平分线的性质定理或逆定理．

3) 过图形上某一点作特定的平分线，构造全等三角形，利用的思维模式是全等变换中的“平移”或“翻转折叠”；（遇垂线及角平分线时延长垂线段，构造等腰三角形）

4) 截长法与补短法，具体做法是在某条线段上截取一条线段与特定线段相等，或是将某条线段延长，是之与特定线段相等，再利用三角形全等的有关性质加以说明．这种作法，适合于证明线段的和、差、倍、分等类的题目．

特殊方法：在求有关三角形的定值一类的问题时，常把某点到原三角形各顶常见辅助线的作法有以下几种：．

手拉手模型

要点一：手拉手模型

特点：由两个等顶角的等腰三角形所组成，并且顶角的

顶点为公共顶点

结论：（1）△ABD ≌△AEC （2）∠α+∠BOC=180°

（3）OA平分∠BOC

变形：

王老师的课堂

2

例1.如图在直线ABC的同一侧作两个等边三角形ABD与BCE，连结AE与CD，证明

（1）DBCABE

(2)DCAE

(3)AE与DC之间的夹角为60

(4)DFBAGB

(5)CFBEGB

(6)BH平分AHC

(7)ACGF//

变式精练1：如图两个等边三角形ABD与BCE，连结AE与CD，

证明（1）DBCABE

（2）DCAE

（3）AE与DC之间的夹角为60

（4）AE与DC的交点设为H,BH平分AHC

变式精练2：如图两个等边三角形ABD与BCE，连结AE与CD，

证明（1）DBCABE

(2）DCAE

(3）AE与DC之间的夹角为60

(4）AE与DC的交点设为H,BH平分AHC

例2：如图，两个正方形ABCD与DEFG,连结CEAG,,二者相交于点H

一、手拉手模型

要点一：手拉手模型

特点：由两个等顶角的等腰三角形所组成，并且顶角的

顶点为公共顶点

结论：（1）△ABD ≌△AEC （2）∠α+∠BOC=180°

（3）OA平分∠BOC

变形：

例1.如图在直线ABC的同一侧作两个等边三角形ABD与BCE，连结AE与CD，证明

（1）DBCABE

(2)DCAE

(3)AE与DC之间的夹角为60

(4)DFBAGB

(5)CFBEGB

(6)BH平分AHC

(7)ACGF//

变式精练1：如图两个等边三角形ABD与BCE，连结AE与CD，

证明（1）DBCABE

（2）DCAE

（3）AE与DC之间的夹角为60

（4）AE与DC的交点设为H,BH平分AHC

变式精练2：如图两个等边三角形ABD与BCE，连结AE与CD，

证明（1）DBCABE

(2）DCAE

(3）AE与DC之间的夹角为60

(4）AE与DC的交点设为H,BH平分AHC

例2：如图，两个正方形ABCD与DEFG,连结CEAG,,二者相交于点H

问：（1）CDEADG是否成立？

（2）AG是否与CE相等？

（3）AG与CE之间的夹角为多少度？

（4）HD是否平分AHE？

例3：如图两个等腰直角三角形ADC与EDG，连结CEAG,,二者相交于点H

问：（1）CDEADG是否成立？

（2）AG是否与CE相等？

（3）AG与CE之间的夹角为多少度？

（4）HD是否平分AHE？

例4：两个等腰三角形ABD与BCE，其中BDAB,,EBCBCBEABD,连结AE与CD，

问：（1）DBCABE是否成立？

（2）AE是否与CD相等？

（3）AE与CD之间的夹角为多少度？

（4）HB是否平分AHC？

二、倍长与中点有关的线段

倍长中线类

☞考点说明：凡是出现中线或类似中线的线段，都可以考虑倍长中线，倍长中线的目的是可以旋转等长度的线段，从而达到将条件进行转化的目的。