杆件的应力
- 格式:ppt
- 大小:4.21 MB
- 文档页数:106
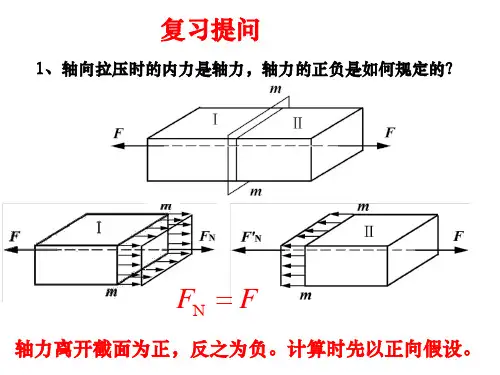
第6章 杆件的应力与强度计算6.1 轴向拉压杆的应力与强度计算6.1.1 应力的概念为了分析内力在截面上的分布情况,从而对杆件的强度进行计算,必须引入应力的概念。
图6-1(a )所示的受力体代表任一受力构件。
pc)F图6-1由于截面上内力的分布一般不是均匀的,所以平均应力m p 与所取小面积A ∆的大小有关。
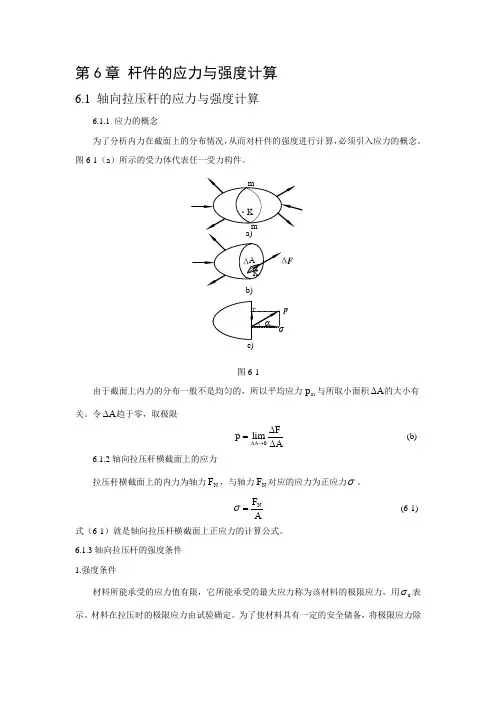
令A ∆趋于零,取极限0limA Fp A∆→∆=∆ (b)6.1.2轴向拉压杆横截面上的应力拉压杆横截面上的内力为轴力N F ,与轴力N F 对应的应力为正应力σ。
NF Aσ=(6-1) 式(6-1)就是轴向拉压杆横截面上正应力的计算公式。
6.1.3轴向拉压杆的强度条件 1.强度条件材料所能承受的应力值有限,它所能承受的最大应力称为该材料的极限应力,用u σ表示。
材料在拉压时的极限应力由试验确定。
为了使材料具有一定的安全储备,将极限应力除以大于1的系数n ,作为材料允许承受的最大应力值,称为材料的许用应力,以符号[]σ表示,即u []nσσ=(6-2)式中n 称为安全系数。
为了确保拉压杆不致因强度不足而破坏,应使其最大工作应力max σ不超过材料的许用应力,即Nmax F Aσ=≤[]σ (6-3) 2.强度条件的三方面应用(1) 强度校核:杆件的最大工作应力不应超过许用应力,即Nmax F Aσ=≤[]σ (2) 选择截面尺寸 : 由强度条件式(6-3),可得A ≥N[]F σ 式中A 为实际选用的横截面积,(3) 确定许用荷载: 由强度条件可知,杆件允许承受的最大轴力N []F 的范围为N F ≤[]A σ6.2材料在轴向拉压时的力学性质在计算拉压杆的强度与变形时,要涉及材料的极限应力u σ和弹性模量E 等,这些反映材料在受力过程中所表现出的有关性质,统称为材料的力学性质。
6.2.1低碳钢在拉伸时的力学性质1.拉伸图与应力-应变曲线将试件装入试验机的夹头后启动机器,使试件受到从零开始缓慢增加的拉力F 作用,试件在标距l 长度内产生相应的变形l ∆。

杆件应力比
杆件应力比是一种计算杆件受力情况的方法。
它是指在某一截面上的应力与材料允许的最大应力之比。
杆件应力比的计算公式如下:
应力比 = 杆件受力 / 杆件的允许最大应力
其中,杆件受力是指杆件所受的外力,可以是拉力、压力或弯矩等;杆件的允许最大应力是指杆件所选用的材料在受力状态下所能承受的最大应力。
通过计算杆件应力比,我们可以评估杆件是否安全:如果应力比小于1,说明杆件受力情况在允许范围内,是安全的;如果应力比大于1,说明杆件受力超过了材料的承载能力,存在安全隐患。
因此,在设计和使用杆件时,需要对杆件的受力情况进行计算和分析,确保杆件应力比在安全范围内。
这可以有效预防杆件的断裂和事故的发生,保障工程的正常运行。







理论力学中的杆件受力分析与扭矩计算理论力学是研究物体运动和受力的经典物理学分支。
在理论力学中,对于杆件受力分析和扭矩计算有着重要的研究和应用。
本文将从理论力学的角度,探讨杆件受力分析以及扭矩的计算方法。
一、杆件受力分析在理论力学中,杆件是常见的力学结构,主要用于支撑和传递力的作用。
杆件受力分析是研究杆件内部受力情况的过程,其中包括了杆件的静力学平衡和杆件的应力分析。
下面将从这两个方面进行介绍。
1.1 杆件的静力学平衡在进行杆件受力分析时,首先需要保证杆件的静力学平衡。
静力学平衡是指杆件内外的力和扭矩之间的平衡关系。
对于一个静止的杆件而言,其受力平衡方程可以表示为:ΣF_x=0 (1)ΣF_y=0 (2)ΣM=0 (3)其中,ΣF_x和ΣF_y分别表示杆件上的水平力和垂直力之和,ΣM表示杆件上的扭矩之和。
通过这些平衡方程,可以求解得到杆件上各个点的受力情况。
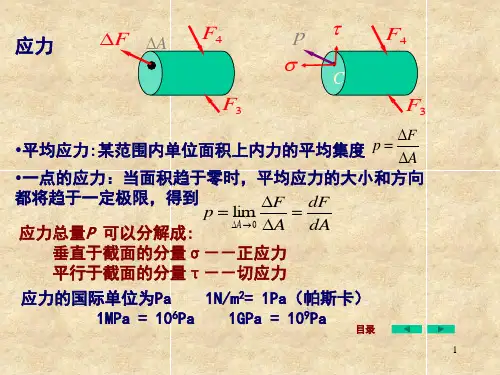
1.2 杆件的应力分析在静力学平衡的基础上,需要对杆件的应力进行进一步的分析。
应力是指单位面积上的力的大小,可分为正应力和剪切应力两种类型。
在杆件受力分析中,常常关注的是杆件上的正应力情况。
根据杆件受力分析的结果,可以利用材料力学的知识,计算出杆件上各个点的正应力大小。
常用的应力计算公式包括弯曲应力、拉压应力和剪切应力等。
二、扭矩的计算方法扭矩是指力对物体产生旋转效应的力矩,是杆件受力分析中重要的参数。
在理论力学中,扭矩的计算常常以杆件的转动为基础。
2.1 扭矩的定义杆件的扭矩可以通过以下公式计算:M = F × d (4)其中,M表示扭矩大小,F表示作用在物体上的力的大小,d表示力作用点到转轴的距离。
扭矩的单位通常为牛顿·米(N·m)或者千克·米(kg·m)。
2.2 扭矩的计算方法杆件的扭矩计算涉及到受力分析和力矩的计算。
在进行扭矩计算时,常需要考虑以下几个方面:(1)确定转轴位置:正确选择与杆件转动有关的转轴位置,转轴的选择将直接影响到扭矩的计算结果。