杆件的应力和强度设计(2)
- 格式:pptx
- 大小:770.34 KB
- 文档页数:35



理论力学中的杆件受力分析与应力计算与设计杆件受力分析与应力计算是理论力学中的重要内容,它在工程设计和结构分析中起着至关重要的作用。
本文将介绍杆件受力分析的基本原理和方法,并探讨应力计算与设计中的一些关键问题。
一、杆件受力分析1. 弹性力学基本原理杆件受力分析的基础是弹性力学的基本原理。
根据胡克定律,杆件的应力与应变成正比。
而根据伯努利梁理论,杆件上的变形与施加的力和几何形状有关。
通过这些基本原理,可以推导出杆件受力分析的基本方程。
2. 杆件的静力学平衡在进行杆件受力分析时,需要根据静力学平衡条件,即力的平衡和力矩的平衡。
通过平衡条件,可以得到各个支点的受力情况,并进一步计算出杆件上各点的内力和外力。
3. 杆件的弯曲和剪切应力杆件在受力时会发生弯曲和剪切的变形,从而引起内力的产生。
根据梁的弯曲理论和材料的力学性质,可以计算出杆件在不同位置的弯曲和剪切应力。
这对于杆件的设计和选择材料具有重要意义。
二、应力计算与设计1. 杆件的选择和尺寸计算在进行杆件的应力计算与设计时,首先需要选择合适的杆件类型和材料。
不同杆件类型和材料的强度和刚度不同,因此需要根据具体情况进行选择。
同时,还需要计算出杆件的尺寸,以满足设计要求和使用条件。
2. 杆件的极限强度和安全系数在进行杆件设计时,需要考虑到杆件的极限强度和安全系数。
极限强度是指杆件能够承受的最大力或应力,而安全系数是指杆件的实际强度与设计所要求的强度之间的比值。
通过合理选择安全系数,可以保证杆件在使用过程中的安全性。
3. 杆件的疲劳和稳定性设计杆件在长期使用过程中会受到疲劳和稳定性的影响。
在进行杆件设计时,需要考虑到疲劳和稳定性的问题,并进行相应的计算和分析。
通过合理设计杆件的结构和选择合适的材料,可以提高杆件的疲劳寿命和稳定性。
三、杆件设计中的一些关键问题1. 材料的选择和力学性质杆件的设计离不开材料的选择和力学性质的了解。
不同材料具有不同的力学性质,如强度、刚度、韧性等。




第6章拉压杆件的应力变形分析与强度设计工程力学学习指导第6章拉压杆件的应力变形分析与强度设计6.1 学习要求与学习目标1. 知道并且能够记住杆件拉伸或压缩时:1) 横截面上的轴力与轴力图;2) 横截面上的正应力;3) 斜截面上的应力;4) 伸长与缩短变形。
2. 掌握并能正确应用拉伸和压缩时杆件横截面上正应力的计算公式。
3. 掌握并能正确应用拉伸和压缩时杆件的变形计算公式。
4. 正确理解并掌握拉伸和压缩时,杆件的强度设计准则,正确应用强度设计准则解决三类强度设计问题。
5. 正确理解拉伸与压缩超静定问题的概念,会应用平衡、变形协调和物性关系求解简单的超静定问题。
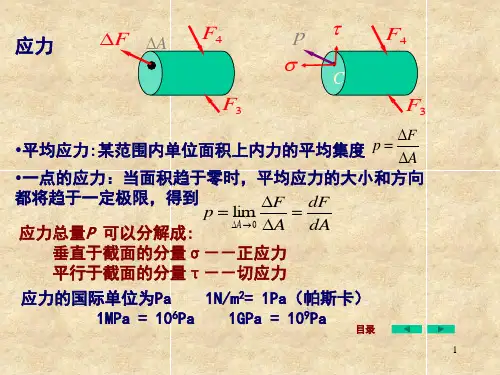
6.2理 论 要 点6.2.1拉伸与压缩杆件的应力与变形1. 应力计算当外力沿着杆件的轴线作用时,其横截面上只有轴力一个内力分量——轴力F N。
与轴力相对应,杆件横截面上将只有正应力。
在很多情形下,杆件在轴力作用下产生均匀的伸长或缩短变形,因此,根据材料均匀性的假定,杆件横截面上的应力为均匀分布,如图6-3所示。
这时横截面上的正应力为AF N =σ 式中,F N 为横截面上的轴力,由截面法求得;A 为横截面面积。
2. 变形计算(1) 绝对变形 弹性模量设一长度为l 、横截面面积为A 的等截面直杆,承受轴向载荷后,其长度变为l 十Δl ,其中Δl 为杆的伸长量(图6-1a)。
试验结果表明:如果所施加的载荷使杆件的变形处于弹性范围内,杆的伸长量Δl 与杆所承受的轴向载荷成正比,如图6-1b 所示。
写成关系式为EAl F l N Δ±= 这是描述弹性范围内杆件承受轴向载荷时力与变形的胡克定律。
其中,F N 为杆横截面上的轴力,当杆件只在两端承受轴向载荷F P 作用时,F N =F P ;E 为杆材料的弹性模量,它与正应力具有相同的单位;EA 称为杆件的拉伸(或压缩)刚度;式中“+”号表示伸长变形;“-”号表示缩短变形。
当拉、压杆有两个以上的外力作用时,需要先画出轴力图,然后按上式分段计算各段的变形,各段变形的代数和即为杆的总伸长量(或缩短量),即()∑=i ii i EA l F l N Δ (2) 相对变形 正应变对于杆件沿长度方向均匀变形的情形,其相对伸长量 Δl/l 表示轴向变形的程度,是这种情形下杆件的正应变,即El EA lF l l x x σε==N Δ= 需要指出的是,上述关于正应变的表达式只适用于杆件各处均匀变形的情形。



第3章杆件的应力与强度判断1、“轴向拉压杆件任意斜截面上的内力作用线一定与杆件的轴线重合”2、“拉杆内只存在均匀分布的正应力,不存在剪应力。
”3、“杆件在轴向拉压时最大正应力发生在横截面上”4、“杆件在轴向拉压时最大剪应力发生在与轴线成45度角的斜截面上”5、“材料的延伸率与试件的尺寸有关。
“6、“没有明显的屈服极限的塑性材料,可以将产生0.2%应变时的应力作为屈服极限。
“7、“构件失效时的极限应力是材料的强度极限。
”8、“对平衡构件,无论应力是否超过弹性极限,剪应力互等定理均成立。
”9、“直杆扭转变形时,横截面的最大剪应力在距截面形心最远处。
”10、“塑性材料圆轴扭转时的失效形式为沿横截面断裂”11、“对于受扭的圆轴,最大剪应力只出现在横截面上”12、”圆轴受扭时,横截面的最大剪应力发生在距截面形心最远处。
”13、“圆轴受扭时,轴内各点均处于纯剪切状态“14、”薄壁圆管与空心圆管的扭转剪应力计算公式完全一样。
”15、”圆轴的扭转变形实际上是剪切变形。
”16、”圆轴扭转时,根据剪应力互等定理,其纵截面上也存在剪应力。
”17、“剪应力互等定理只适用于纯剪状态”18、“传动轴的转速越高,则其横截面的直径应越大”19、“受扭杆件的扭矩仅与杆件所受的外力偶矩有关,而与杆件的材料、横截面的大小以及横截面的形状无关”20、“普通碳钢扭转屈服极限τs=120MPa,剪变模量G=80GPa,则由剪切虎克定律τ=Gγ得到剪应变为γ=1.5×10-3rad”21、“一等直圆杆,当受到扭转时,杆内沿轴线方向会产生拉应变。
”22、“低碳钢圆柱试件受扭时,沿450螺旋面断裂。
”23、“铸铁圆柱试件受扭时,沿横截面断裂”24、“弯曲时梁横截面的中性轴通过截面形心。
”25、“梁的截面如图,其抗弯截面系数为W Z=BH2/6-bh2/6”26、“控制弯曲强度的主要因素是最大弯矩值”27、“设梁某段承受正弯矩的作用,则靠近顶面和靠近底面的纤维分别是伸长的和缩短的”28、“中性轴是梁的中性层与横截面的交线。