导线网平差程序设计
- 格式:ppt
- 大小:891.00 KB
- 文档页数:86

导线网平差及精度评定程序设计平差问题描述背景:导线网平差及精度评定程序设计平差是在测量和测绘工作中常用的一种技术方法。
它是通过对导线网观测数据进行处理和计算,得出导线网的平差结果,并评定其精度,以确保测量结果的准确性和可靠性。
背景:导线网平差及精度评定程序设计平差是在测量和测绘工作中常用的一种技术方法。
它是通过对导线网观测数据进行处理和计算,得出导线网的平差结果,并评定其精度,以确保测量结果的准确性和可靠性。
目的:本文档旨在介绍导线网平差及精度评定程序设计平差的背景和目的。
通过对平差方法和流程的解释,使读者了解导线网平差的基本原理和操作步骤,并了解如何评定导线网平差结果的精度。
这将有助于测量和测绘工作中平差的正确实施,并对测量数据进行科学的分析和解释。
目的:本文档旨在介绍导线网平差及精度评定程序设计平差的背景和目的。
通过对平差方法和流程的解释,使读者了解导线网平差的基本原理和操作步骤,并了解如何评定导线网平差结果的精度。
这将有助于测量和测绘工作中平差的正确实施,并对测量数据进行科学的分析和解释。
目的:本文档旨在介绍导线网平差及精度评定程序设计平差的背景和目的。
通过对平差方法和流程的解释,使读者了解导线网平差的基本原理和操作步骤,并了解如何评定导线网平差结果的精度。
这将有助于测量和测绘工作中平差的正确实施,并对测量数据进行科学的分析和解释。
目的:本文档旨在介绍导线网平差及精度评定程序设计平差的背景和目的。
通过对平差方法和流程的解释,使读者了解导线网平差的基本原理和操作步骤,并了解如何评定导线网平差结果的精度。
这将有助于测量和测绘工作中平差的正确实施,并对测量数据进行科学的分析和解释。
请注意:本文档仅供参考和研究使用,不可用于商业目的或作为法律依据。
建议在实际应用中,根据具体情况和专业要求,进行适当的调整和改进。
请注意:本文档仅供参考和研究使用,不可用于商业目的或作为法律依据。
建议在实际应用中,根据具体情况和专业要求,进行适当的调整和改进。

附合导线平差步骤一、数据处理1.数据输入:将测站、观测角度、观测距离等原始数据输入计算机或平差软件。
2.数据质检:对输入的数据进行初步的质检,检查是否存在错误数据、异常数据等,发现并剔除异常数据。
3.角度数据处理:将观测角度转换为弧度,便于后续计算。
4.距离数据处理:对观测距离进行单位转换,通常将其转换为米或千米。
5.数据配对:将同一测站观测到的角度和距离数据做配对,构成观测组。
6.编点编号:对测站进行编号,便于后续计算。
二、导线控制要素计算1.导线连杆长度计算:根据测站坐标计算导线连杆的几何长度。
2.导线初始点坐标计算:根据导线方位角、连杆长度和已知控制点的坐标计算导线初始点的坐标。
3.导线朝向角计算:根据已知控制点的坐标和导线的方位角,计算导线的朝向角。
三、平差计算1.平差模型确定:选择适当的平差模型,常用的有单位权平差模型、具有不等权的平差模型等。
2.条件方程建立:根据平差模型和导线控制要素的计算结果,建立条件方程组。
3.条件方程系数矩阵确定:根据条件方程组,将其转化为系数矩阵形式。
4.闭合差计算:根据条件方程和系数矩阵,利用最小二乘法计算闭合差,并评估其精度。
5.参数平差:利用闭合差和条件方程系数矩阵,通过参数平差法计算出导线的平差结果。
6.残差计算:根据平差结果和原始观测数据,计算各个观测量的平差残差,并评估其精度。
四、结果分析和判断1.平差结果分析:对平差结果进行查验和分析,判断平差是否满足要求,是否符合实际测量误差的范围。
2.误差判断:根据平差结果和平差残差,判断是否存在异常误差,如超限误差、粗大误差等。
3.解释和修正:对异常误差进行解释和修正,如重新检查测量数据、进行补充观测等。
以上就是附合导线平差步骤的主要内容,通过这些步骤可以得到导线的最佳平差值,为后续的工程测量提供准确的基础数据。
在实际应用中,还需根据具体情况对平差步骤进行调整和优化,以满足实际工程测量的需求。


导线网平差及精度评定程序设计平差引言导线网平差是测量领域中的一项重要工作,它对于保证测量结果的准确性和可靠性具有重要意义。
本文将介绍导线网平差的基本原理和流程,并且设计一个用于导线网平差及精度评定的程序。
程序设计平差流程数据预处理•导入原始测量数据:从测量仪器或文件中导入导线网的原始测量数据。
数据应包括导线长度、角度观测值以及观测仪器的精度等信息。
•数据格式检查:对导入的测量数据进行检查,确保数据的完整性和准确性。
•数据转换:将角度观测值转换为弧度制,便于后续计算。
•建立导线网模型:根据导线的连接关系,建立导线网的拓扑模型。
进行平差计算•确定已知点:根据实际情况,选取导线网中已知点,作为平差计算的基准点。
•建立平差方程:根据导线网模型和已知点的观测值,建立平差方程组。
•进行平差计算:使用最小二乘法或其他适当的方法,求解平差方程组,得到未知点的坐标和精度估计。
•检查计算结果:对平差结果进行检查,确保计算的准确性。
精度评定•计算精度指标:根据计算结果和观测数据的精度,计算导线网的精度指标,如相对误差、中误差等。
•统计分析:对计算结果进行统计分析,得出导线网的整体精度评定。
•生成报告:将计算结果和精度评定结果输出到报告中,方便用户阅读和使用。
程序设计考虑用户界面设计在程序设计过程中,为了方便用户使用,需要设计一个用户友好的界面。
该界面应允许用户导入原始测量数据、选择计算参数、查看计算结果和精度评定结果等。
可以使用图形界面或命令行界面来实现。
程序性能优化导线网平差是一项计算量较大的工作,特别是在处理大规模的导线网时。
为了提高程序的运行效率,可以采用一些优化技术,如矩阵运算优化、并行计算等。
同时,还可以合理选择数据结构和算法,减少计算和存储的开销。
错误处理和异常处理在程序设计中,要考虑到可能出现的数据错误和计算异常情况,为程序添加相应的错误处理和异常处理机制。
当程序发生错误或异常时,应给出合适的提示和错误信息,方便用户及时发现和解决问题。

计算方案的设置一、导线类型:1.闭、附合导线(图1)2.无定向导线(图2)3.支导线(图3)4.特殊导线及导线网、高程网(见数据输入一节),该选项适用于所有的导线,但不计算闭合差。
而且该类型不需要填写未知点数目。
当点击表格最后一行时自动添加一行,计算时删除后面的空行。
5.坐标导线。
指使用全站仪直接观测坐标、高程的闭、附合导线。
6.单面单程水准测量记录计算。
指仅进行单面读数且仅进行往测而无返测的水准测量记录计算。
当数据中没有输入“中视”时可以用作五等、等外水准等的记录计算。
当输入了“中视”时可以用作中平测量等的记录计算。
说明:除“单面单程水准测量记录计算”仅用于低等级的水准测量记录计算外,其它类型选项都可以进行平面及高程的平差计算,输入了平面数据则进行平面的平差,输入了高程数据则进行高程的平差,同时输入则同时平差。
如果不需进行平面的平差,仅计算闭、附合高程路线,可以选择类型为“无定向导线”,或者选择类型为“闭附合导线”但表格中第一行及最后一行数据(均为定向点)不必输入,因为高程路线不需定向点。
二、概算1.对方向、边长进行投影改化及边长的高程归化,也可以只选择其中的一项改正。
2.应选择相应的坐标系统,以及Y坐标是否包含500KM。
选择了概算时,Y坐标不应包含带号。
三、等级与限差1.在选择好导线类型后,再选择平面及高程的等级,以便根据《工程测量规范》自动填写限差等设置。
如果填写的值不符合您所使用的规范,则再修改各项值的设置。
比如现行的《公路勘测规范》的三级导线比《工程测量规范》的三级导线要求要低一些。
2.导线测量平差4.2及以前版本没有设置限差,打开4.2及以前版本时请注意重新设置限差。
四、近似平差与严密平差的选择及近似平差的方位角、边长是否反算1.近似平差:程序先分配角度闭合差再分配坐标增量闭合差,即分别平差法。
2.严密平差:按最小二乘法原理平差。
3.《工程测量规范》规定:一级及以上平面控制网的计算,应采用严密平差法,二级及以下平面控制网,可根据需要采用严密或简化方法平差。

实验三利用mat lab程序设计语言完成某工程导线网平差计算实验数据;某工程项目按城市测量规范(CJJ8-99)不设一个二级导线网作为首级平面控制网,主要技术要求为:平均边长200cm,测角中误差±8,导线全长相对闭合差<1/10000,最弱点的点位中误差不得大于5cm,经过测量得到观测数据,设角度为等精度观测值、测角中误差为山=±8秒,鞭长光电测距、测距中误差为m二± Vsmm,根据所学的‘误差理论与测量平差基础'提出一个最佳的平差方案,利用matlab完成该网的严密平差级精度评定计算;平差程序设计思路:1采用间接平差方法,12个点的坐标的平差值作为参数.利用matlab进行坐标反算,求出已知坐标方位角;根据已知图形各观测方向方位角;2计算各待定点的近似坐标,然后反算出近似方位角,近似边. 计算各边坐标方位角改正数系数;3确定角和边的权,角度权Pj=1 ;边长权Ps=100/S;4计算角度和边长的误差方程系数和常数项,列出误差方程系数矩阵 B,算出Nbb=B’ PB,W=B’ Pl,参数改正数 x=inv(Nbb)*W;角度和边长改正数V=Bx-l; 6建立法方程和解算x,计算坐标平差值,精度计算;程序代码以及说明:s10=;s20=;s30=;s40=;s50=;s60=;s70=;s80=;s90=;s100=;s110=;s120=;s130=;s140=; %已知点间距离Xa=;Ya二;Xb=;Yb=;Xc=;Yc=;Xd=;Yd=;Xe=;Ye=;Xf=;Yf=; %已知点坐标值a0=atand((Yb-Ya)/(Xb-Xa))+180;d0=atand((Yd-Yc)/(Xd-Xc));f0=atand((Yf-Ye)/(Xf-Xe))+360; %坐标反算方位角a1=a0+(163+45/60+4/3600)-180a2=a1+(64+58/60+37/3600)-180;a3=a2+(250+18/60+11/3600)-180;a4=a3+(103+57/60+34/3600)-180;a5=d0+(83+8/60+5/3600)+180;a6=a5+(258+54/60+18/3600)-180-360;a7=a6+(249+13/60+17/3600)-180;a8=a7+(207+32/60+34/3600)-180;a9=a8+(169+10/60+30/3600)-180;a10=a9+(98+22/60+4/3600)-180;a12=f0+(111+14/60+23/3600)-180;a13=a12+(79+20/60+18/3600)-180;a14=a13+(268+6/60+4/3600)-180;a15=a14+(180+41/60+18/3600)-180; %推算个点方位角 aa=[a1 a2 a3 a4 a5 a6 a7 a8 a9 a10 a12 a13 a14 a15]'X20=Xb+s10*cosd(a1);X30=X20+s20*cosd(a2);X40=X30+s30*cosd(a3);X50a=X40+s40*cosd(a4);X60=Xd+s50*cosd(a5);X70=X60+s60*cosd(a6);X80=X70+s70*cosd(a7);X90=X80+s80*cosd(a8);X100=X90+s90*cosd(a9);X50c=X100+s100*cosd(a10);X130二Xf+s110*cosd(a12);X140=X130+s120*cosd(a13);X150=X140+s130*cosd(a14);X50e=X150+s140*cosd(a15); %各点横坐标近似值X0=[X20 X30 X40 X60 X70 X80 X90 X100 X130 X140 X150 X50a X50c X50e]'Y20=Yb+s10*sind(a1);Y30=Y20+s20*sind(a2);Y40=Y30+s30*sind(a3);Y50a=Y40+s40*sind(a4);Y60=Yd+s50*sind(a5);Y70=Y60+s60*sind(a6);Y80=Y70+s70*sind(a7);Y90=Y80+s80*sind(a8);Y100=Y90+s90*sind(a9);Y50c=Y100+s100*sind(a10);Y130=Yf+s110*sind(a12);Y140=Y130+s120*sind(a13);Y150=Y140+s130*sind(a14);Y50e=Y150+s140*sind(a15); %个点从坐标近似值Y0=[Y20 Y30 Y40 Y60 Y70 Y80 Y90 Y100 Y130 Y140 Y150 Y50a Y50c Y50e]'P=[X0 Y0];X50=(X50a+X50c+X50e)/3Y50=(Y50a+Y50c+Y50e)/3s4二sqrt((Y40-Y50)"2+(X40-X50厂2);si二sqrt((Y100-Y50厂2+(X100-X50厂2);s14二sqrt((Y150-Y50)"2+(X150-X50厂2);A1=[cosd(a1) cosd(a2) cosd(a3) cosd(a4) cos(a5) cosd(a6) cosd(a7) cosd(a8) cosd(a9) cosd(a10) cosd(a12) cosd(a13) cosd(a14) cosd(a15)]';B11=[sind(a1) sind(a2) sind(a3) sind(a4) sin(a5) sind(a6) sind(a7) sind(a8) sind(a9) sind(a10) sind(a12) sind(a13) sind(a14) sind(a15)]';s=blkdiag(s10,s20,s30,s4,s50,s60,s70,s80,s90,s10',s110,s120,s130,s14);a=*inv(s)*B11b=*inv(s)*A1ab4=atand((Y50-Y40)/(X50-X40))+180;ab10=atand((Y50-Y100)/(X50-X100));ab14=atand((Y50-Y150)/(X50-X150))+360;m4=ab4-a3+180;m10=ab10-a9+180;m11=ab4-ab10;m15=ab14-a14+180;m16=ab10-ab14+360;m04=103+57/60+34/3600;m010=98+22/60+4/3600;m011=94+53/60+50/3600;m015=180+41/60+18/3600;m016=ab10-ab14+360;l=[0 0 0 m4-103-57/60-34/3600 0 0 0 0 0 m10-98-22/60-4/3600 m11-94-53/60-50/3600 0 0 0 m15T80-41/60T8/3600m16-103-23/60-8/3600 0 0 0 s40-s4 0 0 0 0 0 s100-s1 0 0 0 s140-s14]';e1=(abs(X20-Xb))/s10;e2=(abs(X30-X20))/s20;e3=(abs(X40-X30))/s30;e4=(abs(X50-X40))/s4;e5=(abs(X60-Xd))/s50;e6= (abs(X70-X60))/s60;e7=(abs(X80-X70))/s70;e8=(abs(X90-X80))/s80;e9=(abs(X100-X90))/s90;e10=(abs(X50-X100))/s1;e11=(abs(X130-Xf))/s110;e12=(abs(X140-X130 ))/s120;e13=(abs(X150-X140))/s130;e14=(abs(X50-X150))/s 14;e=[e1 e2 e3 e4 e5 e6 e7 e8 e9 e10 e11 e12 e13 e14]' m1=(abs(Y20-Yb))/s10;m2=(abs(Y30-Y20))/s20;m3=(abs(Y40-Y30))/s30;m4=(abs(Y50-Y40))/s4;m5=(abs(Y60-Yd))/s50;m6= (abs(Y70-Y60))/s60;m7=(abs(Y80-Y70))/s70;m8=(abs(Y90-Y80))/s80;m9=(abs(Y100-Y90))/s90;m10=(abs(Y50-Y100))/s1;m11=(abs(Y130-Yf))/s110;m12=(abs(Y140-Y130 ))/s120;m13=(abs(Y150-Y140))/s130;m14=(abs(Y50-Y150))/s 14;m=[m1 m2 m3 m4 m5 m6 m7 m8 m9 m10 m11 m12 m13 m14]' % 以上为求得误差方程系数B=[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0%系数矩阵B0 0 ]P=blkdiag(1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,100/s10,100/s 20,100/s30,100/s40,100/s50,100/s60,100/s70,100/s80,100/ s90,100/s100,100/s110,100/s120,100/s130,100/s140); %定义权矩阵Nbb二B'*P*BW=B'*P*l;x=inv(Nbb)*WV=B*x-l;inv(Nbb);Y=V'*P*V;O二sqrt(Y/6)*3600 %精度评定计算结果:平差值坐标X:+003 *Qx1= Qy1= Qx2= Qy2= ……Qx15= Qy15=。

《测量平差程序》课程设计(报告)学生姓名:罗正材学号:专业:2011级测绘工程指导教师:肖东升目录一、前言 (3)二、平差程序的基本要求 (3)三、平差程序模块化 (3)四、平差中的重要函数 (4)五、结论 (7)六、部分源代码 (7)一、前言随着测绘科学技术的不断发展,在测量数据的处理中产生很多种平差的方法。
在本文中,附合导线近似平差程序是利用C++编程实现的,我们需要将导线网的已知数据信息按照特定的规则输入到.txt文本中,利用C++程序读取文本数据信息后,对其进行一系列的平差计算,最终获得平差后的结果,并以.txt文本的形式输出且保存,这样就可为测量工作提供一定的参考,还能为测绘数据的管理带来帮助。
二、平差程序的基本要求平差程序设计与其它程序设计相同,应当满足一定的要求。
(1)程序逻辑结构简单,清晰易读,符合结构化程序设计要求,便于扩展;(2)运算速度快,占用内存小,内外存之间的交换不宜过于频繁;(3)数学模型及计算方法正确、先进,计算结果精度高;(4)适应性强,便于移植,充分考虑各种可能形式,尽量满足不同要求与需要;(5)方便用户,操作简便。
数据输入与用户作业方式与习惯相统一,输出明了、齐全;尽量减少手工处理工作量,操作简便;人机交互性要强。
上述要求,既体现在平差程序的总体设计中,也贯穿于平差程序设计的各个环节中。
三、平差程序模块化图1四、平差中的重要函数(一)、角度制与弧度制的相互转化C /C ++程序设计中,关于角度的计算以弧度制为单位,而在测量以及具体工作中我们通常习惯以角度制为单位。
这样,在数据处理中,经常需要在角度制与弧度制之间进行相互转化。
这里,我们利用C /C ++数学函数库中的相关函数完成这两种功能。
这里,我们使用double 类型数据表示角度制数和弧度制数。
例如:123度44分秒,用double图21.角度化弧度函数double d _h (double angle ) 度化角度函数double h _d (double angle ) 方向交会已知条件:两个点的近似坐标,这两个点到未知点的方位角,如图3所示图3 两方向交会根据图,设11αtg k =,22αtg k =,则很容易写出⎪⎪⎩⎪⎪⎨⎧--=--=B P B PA P A P x x y y k x x y y k 21 整理该式,得两方向交会的的计算公式 ⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛--B B A A P P y x k y x k y x k k 212111()对()式计算,即可得到未知点的近似坐标。

导线平差计算1 简介闭合导线和附合导线是长输管道站场和穿跨越测量常用的控制手段,其优点是可以同时完成平面和高程控制测量。
导线平差原理请查阅相关文献。
不同平差软件的平差方法步骤基本相同,本文件基于南方平差易软件平台介绍导线(闭合导线、附合导线是最简单的导线控制网)平差的操作方法。
2 规范性引用文件下列文件中的条款通过本标准的引用而成为本标准的条款。
●《长距离输油输气管道测量规范》(SY/T 0055-2003)●《工程测量规范》(GB 50026-2007)3 操作步骤(1)录入数据录入数据是将导线测量数据录入平差软件。
可以采用手工或文件方式录入(建议采用后者,选菜单“文件/打开”)。
其数据格式如下:[NET] 控制网信息[P ARA] 控制网参数[STATION]坐标和高程信息(11表示高程已知,如果无坐标则无法在平差易中看到和输出地图)[OBSER] 观测的转角、平距、高差等信息下图为导入数据窗口:图3-1 导入数据窗口(2)坐标推算(F3)选菜单“平差/推算坐标”,根据已知条件(测站点信息和观测信息)推算出待测点的近似坐标。
为构建动态网图和导线平差作基础。
(3)概算选菜单“平差/选择概算”→配置概算参数→输出概算结果。
下图为“选择概算”的配置参数窗口:图3-2 配置概算参数(4)调整观测数据将概算结果调整到输入的观测数据中,重新导入。
(5)计算方案的选择对于同时包含了平面数据和高程数据的导线, 一般处理过程应为:先进行平面处理, 然后在高程处理时软件会使用已经较为准确的平面数据(如距离等)来处理高程数据。
对精度要求很高的平面高程混合平差,您也可以在平面和高程处理间多次切换,迭代出精确的结果(但建议平面和高程分开了平差)。
针对导线平差,需要设置中误差及仪器参数、高程平差参数、限差及等级内容。
选菜单“平差/平差方案”即可进行参数的设置,如下图:图3-3 平差方案参数设置(6)闭合差计算与检核(F2)根据观测值和设定参数来计算导线的闭合差,从而来检查某条导线是否存在观测粗差或误差。
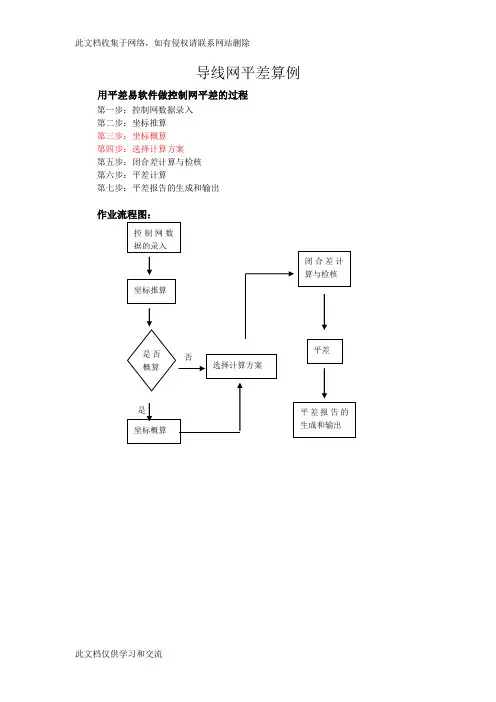
导线网平差算例用平差易软件做控制网平差的过程第一步:控制网数据录入第二步:坐标推算第三步:坐标概算第四步:选择计算方案第五步:闭合差计算与检核第六步:平差计算第七步:平差报告的生成和输出作业流程图:实例1 符合导线实例这是一条符合导线的测量数据和简图,A、B、C和D是已知坐标点,2、3和4是待测的控制点。
测站点角度(°′″) 距离(米)X (米) Y(米)B 8345.8709 5216.6021A 85.30211 1474.4440 7396.2520 5530.00902 254.32322 1424.71703 131.04333 1749.32204 272.20202 1950.4120C 244.18300 4817.6050 9341.4820D 4467.5243 8404.7624导线原始数据表导线图如下:导线图第一步:录入原始数据在平差易软件中输入以上数据,如下图“数据输入”所示:数据输入在测站信息区中输入A、B、C、D、2、3和4号测站点,其中A、B、C、D为已知坐标点,其属性为10,其坐标如“原始数据表”;2、3、4点为待测点,其属性为00,其它信息为空。
如果要考虑温度、气压对边长的影响,就需要在观测信息区中输入每条边的实际温度、气压值,然后通过概算来进行改正。
根据控制网的类型选择数据输入格式,此控制网为边角网,选择边角格式。
如下图“选择格式”所示:选择格式在观测信息区中输入每一个测站点的观测信息,为了节省空间只截取观测信息的部分表格示意图,如下表B、D作为定向点,它没有设站,所以无观测信息,但在测站信息区中必须输入它们的坐标。
以A为测站点,B为定向点时(定向点的方向值必须为零),照准2号点的数据输入如下图“测站A的观测信息”所示:测站A的观测信息以C为测站点,以4号点为定向点时,照准D点的数据输入如下图“测站C的观测信息”所示:测站C的观测信息2号点作为测站点时,以A为定向点,照准3号点,如下图“测站2的观测信息”所示:测站2的观测信息以3号点为测站点,以2号点为定向点时,照准4号点的数据输入如下图“测站3的观测信息”所示:测站3的观测信息以4号点为测站点,以3号点为定向点时,照准C点的数据输入如下图“测站4的观测信息”所示:测站4的观测信息说明:①数据为空或前面已输入过时可以不输入(对向观测例外)②在电子表格中输入数据时,所有零值可以省略不输。

《测量平差程序》课程设计(报告)学生姓名:罗正材学号:专业:2011级测绘工程指导教师:肖东升目录一、前言 (3)二、平差程序的基本要求 (3)三、平差程序模块化 (3)四、平差中的重要函数 (4)五、结论 (7)六、部分源代码 (7)一、前言随着测绘科学技术的不断发展,在测量数据的处理中产生很多种平差的方法。
在本文中,附合导线近似平差程序是利用C++编程实现的,我们需要将导线网的已知数据信息按照特定的规则输入到.txt 文本中,利用C++程序读取文本数据信息后,对其进行一系列的平差计算,最终获得平差后的结果,并以.txt文本的形式输出且保存,这样就可为测量工作提供一定的参考,还能为测绘数据的管理带来帮助。
二、平差程序的基本要求平差程序设计与其它程序设计相同,应当满足一定的要求。
(1)程序逻辑结构简单,清晰易读,符合结构化程序设计要求,便于扩展;(2)运算速度快,占用内存小,内外存之间的交换不宜过于频繁;(3)数学模型及计算方法正确、先进,计算结果精度高;(4)适应性强,便于移植,充分考虑各种可能形式,尽量满足不同要求与需要;(5)方便用户,操作简便。
数据输入与用户作业方式与习惯相统一,输出明了、齐全;尽量减少手工处理工作量,操作简便;人机交互性要强。
上述要求,既体现在平差程序的总体设计中,也贯穿于平差程序设计的各个环节中。
三、平差程序模块化图1四、平差中的重要函数(一)、角度制与弧度制的相互转化C/C++程序设计中,关于角度的计算以弧度制为单位,而在测量以及具体工作中我们通常习惯以角度制为单位。
这样,在数据处理中,经常需要在角度制与弧度制之间进行相互转化。
这里,我们利用C/C++数学函数库math.h中的相关函数完成这两种功能。
这里,我们使用double类型数据表示角度制数和弧度制数。
例如:123度44分58.445秒,用double 类型表示为123.4458445,其中分、秒根据小数位确定。

数据结构课程设计——导线网平差程序的设计与实现设计二:导线网平差程序的设计与实现一、设计目的立足于《数据结构与测绘软件开发》这一课程的课堂教学及其实验课程设计,为着实提高学生基于计算机辅助的方式切实解决工程实际问题的动手能力,通过本实习,一方面,使学生深入了解课堂所学知识,另一方面,通过实践掌握测绘行业软件设计与开发的基本方法,深刻掌握矩阵运算、曲线/曲面拟合的数值解法,掌握不同类型的典型测绘软件设计方法,使得学生初步具备编写测绘软件常用算法的能力以及开发中小规模测绘专业软件的能力。
有导线网如图,观测了14条边长和16个转折角,已知测角精度10βδ''=,测边精度为1.0()()S S m mm δ=。
已知A 、B 、C 、D 、E 、F 点的坐标(无误差),如下表:表1 已知点数据点号 X(m) Y(m)A 5256.953 4520.068B 5163.752 4281.277C 3659.371 3621.210D 4119.879 3891.607E 4581.150 5345.292F 4851.5545316.953表2 角度观测值编号角度观测值(° ′ ″)编号角度观测值(° ′ ″)1 163 45 04 9 169 10 302 64 58 37 10 98 22 043 250 18 11 11 94 53 50 4 103 57 34 12 111 14 235 83 08 05 13 79 20 18三、关键问题描述3.1 未知点近似坐标计算平面控制网进行平差计算时需要计算未知点的近似坐标1.坐标计算公式1、2点的坐标已知,并观测了1-2、1-3的夹角,根据这些数据可以求出3号点坐标根据1、2两点的坐标,可以反算出1、2方向的方位角T12,3号点的坐标为++=++=)sin()cos(121313121313ααT S y y T S x x式子中S13为观测边长,α为观测角度 2.计算流程从读入的数据循环计算未知点的坐标,已计算出的坐标当做已知坐标的点处理参加下次计算,以此类推,逐步计算出未知点的坐标3.实现算法CMatrix CPlaneNetAdjust::XYJS() { CMatrix _XYJS(Pnumber,2); double T12; for(int i=0;i0&&xy[k2].Y>0) { T12=GetT12(k1,k2); } double s12=Gets12(k1,k2); double s13=Gets12(k1,k3); double T13=T12+guancejiao[i].Guancezhi; double dx=s13*cos(T13); double dy=s13*sin(T13); xy[k3].X=xy[k1].X+dx; xy[k3].Y=xy[k1].Y+dy; } for(int i=0;i<="" bdsfid="103" double="" p="" temp1="xy[i].X;" temp2="xy[i].Y;" {="">}return _XYJS;}3.2 误差方程列立1.理论分析平面控制网的误差方程都是非线性方程,必须引入参数近似值将误差方程线性化,取X的充分近似值 0X ,x ?是微小量,在按台劳公式展开时可以略去二次和二次以上的项,而只取至一次项,于是可对非线性平差值观测方程式线性化,于是有如下的式子对于观测角的改正数有对于边长观测值的改正数有2.实现算法如下:CMatrix CPlaneNetAdjust::B() { CMatrix _B1(Lnumber,Pnumber*2); double a; double b; double c; double d; double m; double n; double m1; double n1; for(int i=0;i<="">D A D A D B D B DA DB X X Y Y X X Y Y L ??arctan ??arctan 1-----=-=αα()()22??S AD A D Y Y X X -+-=kjkjk k jk jk j jk jkj jk jk jk y S Y x S Y y S X x S Y ?)(?)(?)(?)(?200200200200"??+??-??-??+=ρρρραδh jhjh h jh jh j jh jh j jh jh jh y S Y x S Y y S X x S Y ?)(?)(?)(?)(?200 200200200"??+??-??-??+=ρρρραδ)(?)("?)("?)("?)("?)("?)("?)(" )("00200200200200200200200200i jk jh h jh jhh jh jh j jh jh j jh jh k jk jkk jk jk j jk jk j jk jk i L y S X x S Y y S X x S Y y S X x S Y y S X xS Y v ---??+?-?-?-+?-?-?-=ααρρρρρρρρi k jkjkk jk jk j jk jk j jk jk i l y S Y x S X y S Y x S X v -?+?+?-?-=000000000jki i S L l -=2002000)()(j k j k jk Y Y X X S -+-=_B1.setValue(i,2*k1,0);_B1.setValue(i,2*k1+1,0);}else{_B1.setValue(i,2*k1,a);_B1.setValue(i,2*k1+1,b);}if(k2<knpnumber)< bdsfid="148" p=""></knpnumber)<> {_B1.setValue(i,2*k2,0);_B1.setValue(i,2*k2+1,0);}else{_B1.setValue(i,2*k2,-a);_B1.setValue(i,2*k2+1,-b);}}for(int i=0;i<tnumber;i++)< bdsfid="160" p=""></tnumber;i++)<>{const double p=206.265;int k1=cezhan[i];int k3=huoshi[i];int k2=qianshi[i];double dx12=xy[k2].X-xy[k1].X;double dy12=xy[k2].Y-xy[k1].Y;double dx13=xy[k3].X-xy[k1].X;double dy13=xy[k3].Y-xy[k1].Y;c=(p*dx13/Gets12(k1,k3)/Gets12(k1,k3)-p*dx12/Gets12(k1,k2)/Gets12(k1,k2));c=-c;d=-p*dy13/Gets12(k1,k3)/Gets12(k1,k3)+p*dy12/Gets12(k1,k2)/Get s12(k1,k2);d=-d;m=-p*dy13/Gets12(k1,k3)/Gets12(k1,k3);m=-m;n=p*dx13/Gets12(k1,k3)/Gets12(k1,k3);n=-n;m1=p*dy12/Gets12(k1,k2)/Gets12(k1,k2);m1=-m1;n1=-p*dx12/Gets12(k1,k2)/Gets12(k1,k2);n1=-n1;if(k1<knpnumber)< bdsfid="183" p=""></knpnumber)<> {_B1.setValue(i+Snumber,2*k1,0);_B1.setValue(i+Snumber,2*k1+1,0);}else if(k1>=knPnumber){_B1.setValue(i+Snumber,2*k1,c);_B1.setValue(i+Snumber,2*k1+1,d);}if(k2<knpnumber)< bdsfid="194" p=""></knpnumber)<> {_B1.setValue(i+Snumber,2*k2,0);_B1.setValue(i+Snumber,2*k2+1,0);}else if(k2>=knPnumber){ _B1.setValue(i+Snumber,2*k2,m1); _B1.setValue(i+Snumber,2*k2+1,n1); } if(k3=knPnumber) { _B1.setValue(i+Snumber,2*k3,m); _B1.setValue(i+Snumber,2*k3+1,n); } }CMatrix _B(Lnumber,2*(Pnumber-knPnumber)); for(int i=0;i<_B1.getRow();i++) { for(int j=2*knPnumber;j<2*Pnumber;j++) { double temp=_B1.getValue(i,j); _B.setValue(i,(j-2*knPnumber),temp); } } return _B;}3.3 法方程构建与解算1.理论分析误差方程系数构成法方程2.实现代码①计算LCMatrix CPlaneNetAdjust::L() { CMatrix _L(Lnumber,1); double l; double s; double s0; for(int i=0;i<="" bdsfid="209" const="" cout<<l<l x B V -=?0?=-Pl B x PB B TTmin =PV V T V L L +=?20σ20?σPV V T double A13; double A;int k1=cezhan[i]; int k2=huoshi[i]; int k3=qianshi[i];A12=GetT12(k1,k2); A13=GetT12(k1,k3); A=GetA(k1,k2,k3); l=A13-A12; if(l<0) { l=pi+l; }if(l>=pi) { l=l-pi; }l=l-A;//cout<<rad_dms(a12)<<" "<<rad_dms(a)<<"<="" "<<rad_dms(a13)<<"="" bdsfid="220" p=""></rad_dms(a12)<<">"<<rad_dms(l)<<endl;< bdsfid="222" p=""></rad_dms(l)<<endl;<>_L.setValue(i+Snumber,0,rad_dms(l));} return _L; }②计算权阵PCMatrix CPlaneNetAdjust::P() { CMatrix _P(Lnumber,Lnumber); for(int i=0;i<="" p="" {="">temp=temp=Cjwucha*Cjwucha/(1*sqrt(bianchang[i].Len))/( 1*sqrt(bianchang[i].Len)); _P.setValue(i,i,temp); } for(int i=Snumber;i<="">3.4 精度估计1.单位权中误差间接平差与条件平差虽采用了不同的函数模型,但它们是在相同的最小乘原理下进行的,所以两法的平差结果总是相等的,这是因为在满足条件下的V 是唯一确定的,故平差值不因方法不同而异。
平差课程设计导线网一、课程目标知识目标:1. 让学生掌握导线网的基本概念,理解其在测量平差中的应用。
2. 学会计算导线网的闭合差、各边长及各角度的改正数,掌握相应的计算公式。
3. 掌握根据导线网计算结果进行精度分析和评定的方法。
技能目标:1. 能够运用所学知识解决实际测量中的导线网问题,具备一定的实践操作能力。
2. 能够独立完成导线网闭合差的计算,熟练运用计算工具进行数据处理。
3. 能够对导线网计算结果进行合理的分析,提出改进措施。
情感态度价值观目标:1. 培养学生对测量平差学科的兴趣,激发他们主动学习的热情。
2. 增强学生的团队合作意识,培养他们在解决问题时相互协作、共同进步的精神。
3. 培养学生严谨的科学态度,使他们认识到测量精度对实际工程的重要性。
课程性质:本课程为测量平差学科的基础课程,以理论教学为主,实践操作为辅。
学生特点:学生已具备一定的测量学基础知识,具有较强的逻辑思维能力和学习兴趣。
教学要求:结合学生特点和课程性质,注重理论与实践相结合,提高学生的实际操作能力。
通过本课程的学习,使学生能够掌握导线网的相关知识,为后续专业课程打下坚实基础。
教学过程中,将目标分解为具体的学习成果,便于教学设计和评估。
二、教学内容1. 导线网基本概念:介绍导线网的定义、分类及其在测量中的应用。
- 教材章节:第二章第二节- 内容列举:导线网的定义、平面导线网、高程导线网等。
2. 导线网闭合差计算:讲解导线网闭合差的计算方法,推导相关公式。
- 教材章节:第二章第三节- 内容列举:闭合差定义、闭合差计算公式、各边长和角度改正数的计算。
3. 导线网精度分析:分析导线网的精度,探讨影响精度的因素及改进措施。
- 教材章节:第二章第四节- 内容列举:精度评定方法、误差来源分析、提高精度的措施。
4. 导线网实践操作:组织学生进行导线网实践操作,巩固理论知识。
- 教材章节:第二章第五节- 内容列举:实践操作步骤、仪器使用、数据处理与分析。
山西水利职业技术学院实习报告题目导线平差的程序设计与实现姓名:孟国娇学号:专业:工程造价1139报告提交日期:山西水利职业技术学院设计任务书学院:土建工程系专业年级:工程造价2011 学生姓名:孟国娇任务下达日期:2012年 2 月20日毕业设计日期:2012年3月12日至2012年6月13日毕业设计题目:导线平差的程序设计与实现毕业设计主要内容和要求:主要内容:(1)测量平差的研究背景及意义;(2)测量平差概述;(3)Excel在单一附和导线近似平差中的应用;(4)Excel在单一附和导线条件平差中的应用;(5)导线网的间接平差理论;(6)导线网平差的结构和函数设计与实现。
设计要求:(1)毕业设计要充分发挥主观能动性,积极思考,主动实践;(2)毕业设计撰写结构要严整,叙述清楚,理论分析适当,数据可靠,研究方法合理,结论正确,论文格式符合规范;(3)研究成果要有一定的实用或参考价值。
院长签字:指导教师签字:摘要随着测绘科学技术的不断发展,在测量数据的处理中产生很多种平差的方法。
在本文中,导线网的近似平差和条件平差的一些简单计算可通过Excel表编制计算公式和编程实现,我们只需在已编好的Excel表中稍作调整和公式修改,并输入已知数据,最终就可得到所需的平差结果,这为测量的内业工作提供了服务和参考;导线网的间接平差程序是利用C++编程实现的,我们需要将导线网的已知数据信息按照特定的规则输入到dat文本中,利用C++程序读取文本数据信息后,对其进行一系列的平差计算,最终获得平差后的结果,并以dat文本的形式输出且保存,这样就可为测量工作提供一定的参考,还能为测绘数据的管理带来帮助。
关键词:导线平差;Excel;C++;程序目录1绪论...............................................................................................................................................1.1研究背景及意义.................................................................................................................1.2国内外研究状况.................................................................................................................1.3本文研究的具体内容.........................................................................................................1.4平差程序相关说明.............................................................................................................1.4.1平差程序计算特点..................................................................................................1.4.2平差程序的基本要求..............................................................................................1.4.3平差程序的结构化设计..........................................................................................1.4.4平差程序模块化......................................................................................................1.4.5平差程序的数据结构.............................................................................................. 2测量平差.......................................................................................................................................2.1测量平差概述.....................................................................................................................2.1.1测量平差..................................................................................................................2.1.2测量平差的函数模型..............................................................................................2.2最小二乘原理.....................................................................................................................2.3条件平差原理.....................................................................................................................2.3.1条件平差的数学模型..............................................................................................2.3.2条件平差原理..........................................................................................................2.3.3条件平差的计算步骤..............................................................................................2.3.4精度评定..................................................................................................................2.4间接平差原理.....................................................................................................................2.4.1间接平差的数学模型..............................................................................................2.4.2间接平差的的一般原理..........................................................................................2.4.3按间接平差法求平差值的计算步骤......................................................................2.4.4精度评定.................................................................................................................. 3Excel在导线平差中的应用.........................................................................................................3.1 Excel在平差中的应用基础...............................................................................................3.1.1 引言.........................................................................................................................3.1.2Excel在平差中的基本应用操作函数...................................................................3.1.3 核心问题的解决及技巧.........................................................................................3.1.4 三角函数在Excel中的处理方法..........................................................................3.1.5 小结.........................................................................................................................3.2Excel在附和导线近似平差中的应用..............................................................................3.2.1 单一附和导线近似平差.........................................................................................3.2.2单一附和导线近似平差实例..................................................................................3.3 Excel在导线网条件平差中的应用...................................................................................3.3.1单一附合导线条件平差..........................................................................................3.3.2边角权的确定及单位权中误差..............................................................................3.3.3单一附和导线条件平差实例.................................................................................. 4导线网的间接平差程序设计与实现 ...........................................................................................4.1矩阵的相关函数.................................................................................................................4.1.1矩阵相乘..................................................................................................................4.1.2矩阵转置..................................................................................................................4.1.3矩阵求逆..................................................................................................................4.1.4矩阵输出..................................................................................................................4.1.5设置实数输出精度..................................................................................................4.2平差中的重要函数.............................................................................................................4.2.1角度制与弧度制的相互转化..................................................................................4.2.2测量正反算函数......................................................................................................4.2.3近似坐标计算..........................................................................................................4.3导线网的平差理论.............................................................................................................4.3.1平差概述..................................................................................................................4.3.2边角网的最小二乘平差..........................................................................................4.4间接平差的结构与函数设计.............................................................................................4.4.1间接平差..................................................................................................................4.4.2结构与函数设计......................................................................................................4.5导线网平差的程序应用.....................................................................................................4.5.1平面网数据的输入格式..........................................................................................4.5.2导线网平差程序应用实例...................................................................................... 5结论与展望 ...................................................................................................................................5.1Excel在导线平差中的应用..............................................................................................5.1.1Excel在导线近似平差中的应用...........................................................................5.1.2Excel在导线网条件平差中的应用.......................................................................5.2C++在导线平差中的应用 .................................................................................................5.3测量平差的展望................................................................................................................ 参考文献........................................................................................................................................... 致谢. (54)1绪论1.1研究背景及意义测量工作是工程施工非常基础、重要的环节,对工程设计、工程施工、工程的验收都发挥着指导性、不可替代的作用。
程序源代码C语言程序:#include <windows.h>#include <stdarg.h>#include <stdio.h>#include <stdlib.h>#include<math.h>#define PI 3.1415926535898#define p 206264.806247#define MAX 50//矩阵的乘法运算MatrixMutiply(double Matrix1[MAX][MAX],double Matrix2[MAX][MAX],double MatrixResult[MAX][MAX],int m1,int m2,int m3){int i,j,k;double Sum;for(i=0;i<m1;i++){for(j=0;j<m3;j++){/*按照矩阵乘法的规则计算结果矩阵的i*j元素*/Sum=0;for(k=0;k<m2;k++)Sum+=Matrix1[i][k]*Matrix2[k][j];MatrixResult[i][j]=Sum;}}//return MatrixResult;}//矩阵的转置运算MatrixT(double Matrix1[MAX][MAX],double T[MAX][MAX],int m1,int m2) {//m1,m2分别是矩阵的行列数int i,j;//double T[50][50];for(i=0;i<m1;i++){for(j=0;j<m2;j++){T[j][i]=Matrix1[i][j];}}//return T;}//矩阵的逆运算void swap(double a,double b){double c=a;a=b;b=c;}double DinV(double A[50][50],int n) //n代表阶数{int i,j,k;double d;int JS[50],IS[50];for (k=0;k<n;k++){d=0;for (i=k;i<n;i++)for (j=k;j<n;j++){if (fabs(A[i][j])>d){d=fabs(A[i][j]);IS[k]=i;JS[k]=j;}}if (d+1.0==1.0)return 0;if (IS[k]!=k)for (j=0;j<n;j++)swap(A[k][j],A[IS[k]][j]);if (JS[k]!=k)for (i=0;i<n;i++)swap(A[i][k],A[i][JS[k]]);A[k][k]=1/A[k][k];for (j=0;j<n;j++)if (j!=k) A[k][j]=A[k][j]*A[k][k];for (i=0;i<n;i++)if (i!=k)for (j=0;j<n;j++)if (j!=k) A[i][j]=A[i][j]-A[i][k]*A[k][j];for (i=0;i<n;i++)if (i!=k) A[i][k]=-A[i][k]*A[k][k]; }for (k=n-1;k>=0;k--){for (j=0;j<n;j++)if (JS[k]!=k) swap(A[k][j],A[JS[k]][j]);for (i=0;i<n;i++)if (IS[k]!=k)swap(A[i][k],A[i][IS[k]]);}}//将度分秒连写的角度化为弧度值double jd_hd(double D,double F,double M){//int dd=(int)((int)B/10000); //提取度值//int ff=(int)(((int)B-dd*10000)/100); //提取分值//double mm=B-dd*10000-ff*100;//提取秒值double B;B=(D*3600.0+F*60.0+M)/p;//角度化弧度return B;}main(){double D,F,M,sigma_beta=2.0,sigma_s;//scanf("%f%f%f",&D,&F,&M);//printf("%f",jd_hd(D,F,M));doublebeta[50],alf[50],alfo[50],s[50],so[50],Xo[50],Yo[50],B[50][50]={0.0},L[50][50],P[50][50 ]={0.0},c[50][50]={0.0},wx=0.0;//此处为Xo Yo,B矩阵赋初值为零beta代表夹角,alf方位角,alfo方位角近似值,s距离观测值,so距离近似值//Xo Yo坐标近似值,B[50][50]误差矩阵,L[50]为L矩阵,P[50][50]为权阵,c[1][30]代表限制条件的系数阵,w代表限制条件常数项doubleNbb[50][50],Ncc[50][50],W[50][50],Ks,xgu[50][50],Xgu[30][1],Ygu[30][1],V[50][50],sigma_gu,Q[50][50],sigma_xy[50][50];alf[0]=PI;alfo[0]=PI;int i,j,m1,m2,m3;//将测量数据导入,并存入相应数组FILE *fp3;char strline[100]; //读取文件每行的bufferint du[100],fen[100],miao[100];double bian[100];i=0,j=1;if((fp3=fopen("D:\\111\\测量数据.txt","r"))==NULL) //文件位置和文件名{printf("文件不存在!");return 0;}while(!feof(fp3)) //判断文件是否已到末尾{fgets(strline,100,fp3); //读取一行sscanf(strline,"%d %d %d %lf",&du[i],&fen[i],&miao[i],&bian[i]); //从文件读取到的一行数据分别存放在两个数组中i++;}fclose(fp3);while(1){//printf("\n%d\t%d\t%d\t%lf",du[j],fen[j],miao[j],bian[j]);beta[j-1]=jd_hd(du[j],fen[j],miao[j]);s[j-1]=bian[j];j++;if(j>=i){break;}}Xo[0]=5000.0;Yo[0]=5000.0;Xo[15]=5000.0;Yo[15]=5000.0;so[0]=s[0];//用来求未知点坐标近似值for(i=1;i<15;i++){alf[i]=alf[i-1]+beta[i]-PI;if(alf[i]>=(2*PI)){alf[i]=alf[i]-2*PI;}Xo[i]=Xo[i-1]+s[i-1]*cos(alf[i-1]);Yo[i]=Yo[i-1]+s[i-1]*sin(alf[i-1]);//printf("X=%f\t",Xo[i]);}for(i=1;i<15;i++){//求近似距离so[i]=sqrt((Yo[i+1]-Yo[i])*(Yo[i+1]-Yo[i])+(Xo[i+1]-Xo[i])*(Xo[i+1]-Xo[i]));//求近似方位角,分象限进行讨论if((Yo[i+1]-Yo[i])>0&&(Xo[i+1]-Xo[i])>0)//第一象限{alfo[i]=atan((Yo[i+1]-Yo[i])/(Xo[i+1]-Xo[i]));}else if((Yo[i+1]-Yo[i])>0&&(Xo[i+1]-Xo[i])<0)//第二象限{alfo[i]=atan((Yo[i+1]-Yo[i])/(Xo[i+1]-Xo[i]))+PI;}else if((Yo[i+1]-Yo[i])<0&&(Xo[i+1]-Xo[i])>0)//第三象限{alfo[i]=atan((Yo[i+1]-Yo[i])/(Xo[i+1]-Xo[i]))+2*PI;}else //((Yo[i]-Yo[i-1])<0&&(Xo[i]-Xo[i-1])<0)//第四象限{alfo[i]=atan((Yo[i+1]-Yo[i])/(Xo[i+1]-Xo[i]))+PI;}//printf("alf=%f\t",alfo[i]);//printf("so=%f\t",so[i]);}//求B矩阵//将第一个角度的系数单独算出j=0;//B[0][j]=0.0;((Yo[14]-Yo[0])/(so[14]*so[14]))*p/1000.0;//B[0][j+1]=0.0;-1*((Xo[14]-Xo[0])/(so[14]*so[14]))*p/1000.0;B[0][j]=-1*(Yo[1]-Yo[0])/(so[0]*so[0])*p/1000.0;//B[0][j+1]=(Xo[1]-Xo[0])/(so[0]*so[0])*p/1000.0;B[0][26]=((Yo[14]-Yo[0])/(so[14]*so[14]))*p/1000.0;B[0][27]=-1*(Xo[14]-Xo[0])/(so[14]*so[14])*p/1000.0;//将第二个角度的系数单独算出B[1][j]=((Yo[2]-Yo[1])/(so[1]*so[1])-(Yo[0]-Yo[1])/(so[0]*so[0]))*p/1000.0;//B[1][j+1]=-1*((Xo[2]-Xo[1])/(so[1]*so[1])-(Xo[0]-Xo[1])/(so[0]*so[0]))*p/1000.0 ;B[1][j+2]=-1*((Yo[2]-Yo[1])/(so[1]*so[1]))*p/1000.0;B[1][j+3]=((Xo[2]-Xo[1])/(so[1]*so[1]))*p/1000.0;//求其他角度改正的系数for(i=2;i<15;i++){if(i<14){B[i][j]=((Yo[i-1]-Yo[i])/(so[i-1]*so[i-1]))*p/1000.0;B[i][j+1]=-1*((Xo[i-1]-Xo[i])/(so[i-1]*so[i-1]))*p/1000.0;B[i][j+2]=((Yo[i+1]-Yo[i])/(so[i]*so[i])-(Yo[i-1]-Yo[i])/(so[i-1]*so[i-1]))*p/1000.0;B[i][j+3]=-1*((Xo[i+1]-Xo[i])/(so[i]*so[i])-(Xo[i-1]-Xo[i])/(so[i-1]*so[i-1]))*p/1000. 0;B[i][j+4]=-1*((Yo[i+1]-Yo[i])/(so[i]*so[i]))*p/1000.0;B[i][j+5]=(Xo[i+1]-Xo[i])/(so[i]*so[i])*p/1000.0;}else{B[i][j]=(Yo[i-1]-Yo[i])/(so[i-1]*so[i-1])*p/1000.0;B[i][j+1]=-1*((Xo[i-1]-Xo[i])/(so[i-1]*so[i-1]))*p/1000.0;B[i][j+2]=((Yo[i+1]-Yo[i])/(so[i]*so[i])-(Yo[i-1]-Yo[i])/(so[i-1]*so[i-1]))*p/1000.0;B[i][j+3]=-1*((Xo[i+1]-Xo[i])/(so[i]*so[i])-(Xo[i-1]-Xo[i])/(so[i-1]*so[i-1]))*p/1000. 0;}j=j+2;}B[2][1]=0.0;//求边长改正的系数j=0;//将第一个边长的系数单独算出B[i][j]=(Xo[1]-Xo[0])/so[0];//B[i][j+1]=(Yo[1]-Yo[0])/so[0]; //(Yo[1]-Yo[0])/(so[0]*so[0]); i=i+1;for(i;i<30;i++){if(i<29){B[i][j]=-1*(Xo[i-14]-Xo[i-15])/so[i-15];B[i][j+1]=-1*(Yo[i-14]-Yo[i-15])/so[i-15];B[i][j+2]=-1*B[i][j];B[i][j+3]=-1*B[i][j+1];}else{B[i][j]=-1*(Xo[i-14]-Xo[i-15])/so[i-15];B[i][j+1]=-1*(Yo[i-14]-Yo[i-15])/so[i-15];}j=j+2;}B[16][1]=0.0;for(j=1;j<27;j++){for(i=0;i<30;i++){B[i][j]=B[i][j+1];}}//求L矩阵L[0][0]=(beta[0]-(alfo[0]-alfo[14]+PI))*p;for(i=1;i<30;i++){if(i<15){L[i][0]=(beta[i]-(alfo[i]-alfo[i-1]+PI))*p;if(L[i][0]>PI*p){L[i][0]=(L[i][0]-2*PI*p);}L[i][0]=L[i][0];}else{L[i][0]=(s[i-15]-so[i-15])*1000.0;}}//求权阵Pfor(i=0;i<30;i++){if(i<15){P[i][i]=1;}else{sigma_s=5+10*0.000001*s[i-15]*1000; //单位为(''/mm)的平方P[i][i]=sigma_beta*sigma_beta/(sigma_s*sigma_s);}}double Tb[50][50],Tc[50][50],MatrixResult[50][50],TV[50][50];doubletemp1[MAX][MAX],temp2[MAX][MAX],temp3[MAX][MAX],temp4[MAX][MAX],temp5[MAX][MAX];//计算Nbb矩阵,W矩阵m1=30;m2=28;MatrixT(B,Tb,m1,m2);m3=30;MatrixMutiply(Tb,P,temp1,m2,m1,m3);m3=m2;m1=m2;m2=30;MatrixMutiply(temp1,B,Nbb,m1,m2,m3);m1=27;m2=30;m3=1;MatrixMutiply(temp1,L,W,m1,m2,m3);//矩阵输出D:\\111\\导线网输出数据3027.txt文本FILE *fp;fp=fopen("D:\\111\\导线网输出数据3027.txt","w");if(fp!=NULL){fprintf(fp,"距离近似值so(单位:m):\t");fprintf(fp,"方位角近似值alfo(单位:弧度):\n");for(i=0;i<15;i++){fprintf(fp,"%4.12lf\t",so[i]);fprintf(fp,"%.12lf\n",alfo[i]);}fprintf(fp,"Xo(单位:mm):\t");fprintf(fp,"Yo(单位:mm):");fprintf(fp,"\n");for(i=0;i<15;i++){fprintf(fp,"%.6lf\t",Xo[i]);fprintf(fp,"%.6lf",Yo[i]);fprintf(fp,"\n");}fprintf(fp,"B矩阵:");fprintf(fp,"\n");for(i=0;i<30;i++){for(j=0;j<27;j++){fprintf(fp,"%.6f ",B[i][j]);}fprintf(fp,"\n");}fprintf(fp,"L矩阵(单位:秒和mm):"); fprintf(fp,"\n");for(i=0;i<30;i++){fprintf(fp,"%.6lf ",L[i][0]);fprintf(fp,"\n");}fprintf(fp,"P矩阵:");fprintf(fp,"\n");for(i=0;i<30;i++){for(j=0;j<30;j++){fprintf(fp,"%.6f ",P[i][j]);}fprintf(fp,"\n");}fprintf(fp,"Nbb矩阵:");fprintf(fp,"\n");for(i=0;i<27;i++){for(j=0;j<27;j++){fprintf(fp,"%.12f ",Nbb[i][j]);}fprintf(fp,"\n");}fclose(fp); //写入完毕,关闭文件}DinV(Nbb,27); //MatrixResult=c * Nbb的逆,此时Nbb已经变成Nbb的逆//计算x^m1=27;m2=27;m3=1;MatrixMutiply(Nbb,W,xgu,m1,m2,m3);double xgu28[50][50],sigma_xy28[50][50];xgu28[0][0]=xgu[0][0];for(i=1;i<27;i++){xgu28[i+1][0]=xgu[i][0];}xgu28[1][0]=0.0;//计算X^(即Xgu估值)Xgu[0][0]=5000.0;Ygu[0][0]=5000.0;for(i=0;i<14;i++){Xgu[i+1][0]=Xo[i+1]+xgu28[2*i][0]/1000.0;Ygu[i+1][0]=Yo[i+1]+xgu28[2*i+1][0]/1000.0; }//精度评定m1=30;m2=27;m3=1;MatrixMutiply(B,xgu,temp5,m1,m2,m3);for(i=0;i<30;i++){if(i<15){V[i][0]=(temp5[i][0]-L[i][0]);}else{V[i][0]=(temp5[i][0]-L[i][0]);}}m1=30;m2=1;MatrixT(V,TV,m1,m2);m1=1;m2=30;m3=30;MatrixMutiply(TV,P,temp4,m1,m2,m3);m1=1;m2=30;m3=1;MatrixMutiply(temp4,V,temp4,m1,m2,m3);sigma_gu=sqrt(temp4[0][0]/3); //单位权中误差double vv=0.0;for (i=0;i<15;i++){for (j=0;j<1;j++){vv=vv+V[i][j];}//puts("");}printf("%lf\t",vv);for(i=0;i<27;i++){for(j=0;j<27;j++){Q[i][j]=Nbb[i][j];}}for(i=0;i<27;i++){sigma_xy[i][0]=sqrt(Q[i][i])*sigma_gu; //坐标平差值中误差//printf("%lf\n",sigma_xy[i][0]);}sigma_xy28[0][0]=sigma_xy[0][0];for(i=1;i<27;i++){sigma_xy28[i+1][0]=sigma_xy[i][0];}sigma_xy28[1][0]=0.0;//printf("%.10lf\n",Ncc[0][0]);FILE *fp1;fp1=fopen("D:\\111\\导线网输出数据3027.txt","a"); fprintf(fp1,"Nbb的逆:");fprintf(fp1,"\n");for(i=0;i<27;i++){for(j=0;j<27;j++){fprintf(fp1,"%lf ",Nbb[i][j]);}fprintf(fp1,"\n");}fprintf(fp1,"W:");fprintf(fp1,"\n");for(i=0;i<27;i++){for(j=0;j<1;j++){fprintf(fp1,"%.12lf ",W[i][j]);}fprintf(fp1,"\n");}fprintf(fp1,"x^(单位:mm):");fprintf(fp1,"\n");for(i=0;i<28;i++){for(j=0;j<1;j++){fprintf(fp1,"%.10lf ",xgu28[i][j]);}fprintf(fp1,"\n");}fprintf(fp1,"V(单位:秒和mm):");fprintf(fp1,"\n");for(i=0;i<30;i++){for(j=0;j<1;j++){fprintf(fp1,"%.10lf ",V[i][j]);}fprintf(fp1,"\n");}fprintf(fp1,"X^(单位:m):\t");fprintf(fp1,"Y^(单位:m):");fprintf(fp1,"\n");for(i=0;i<15;i++){for(j=0;j<1;j++){fprintf(fp1,"%.6lf\t",Xgu[i][j]);fprintf(fp1,"%.6lf",Ygu[i][j]);}fprintf(fp1,"\n");}fprintf(fp1,"单位权中误差(单位:mm):\n"); fprintf(fp1,"%.10lf\n",sigma_gu);fprintf(fp1,"X坐标平差值中误差(单位:mm):\t");fprintf(fp1,"Y坐标平差值中误差(单位:mm):");fprintf(fp1,"\n");for(i=0;i<13;i++){fprintf(fp1,"%lf\t\t",sigma_xy28[2*i][0]);fprintf(fp1,"%lf",sigma_xy28[2*i+1][0]);fprintf(fp1,"\n");}}C语言画图程序//导线网概略图#include <stdio.h>#include <windows.h>#include <math.h>#define NUM 30LRESULT CALLBACK WndProc (HWND, UINT, WPARAM, LPARAM) ;int WINAPI WinMain (HINSTANCE hInstance, HINSTANCE hPrevInstance, PSTR szCmdLine, int iCmdShow){static char szAppName[] = "SineWave" ;HWND hwnd ;MSG msg ;WNDCLASSEX wndclass ;wndclass.cbSize = sizeof (wndclass) ;wndclass.style = CS_HREDRAW | CS_VREDRAW ;wndclass.lpfnWndProc = WndProc ;wndclass.cbClsExtra = 0 ;wndclass.cbWndExtra = 0 ;wndclass.hInstance = hInstance ;wndclass.hIcon = LoadIcon (NULL, IDI_APPLICATION) ;wndclass.hCursor = LoadCursor (NULL, IDC_ARROW) ;wndclass.hbrBackground = (HBRUSH) GetStockObject (WHITE_BRUSH) ; wndclass.lpszMenuName = NULL ;wndclass.lpszClassName = szAppName ;wndclass.hIconSm = LoadIcon (NULL, IDI_APPLICATION) ;RegisterClassEx (&wndclass) ;hwnd = CreateWindow (szAppName, "控制网图",WS_OVERLAPPEDWINDOW,CW_USEDEFAULT, CW_USEDEFAULT,CW_USEDEFAULT, CW_USEDEFAULT,NULL, NULL, hInstance, NULL) ;ShowWindow (hwnd, iCmdShow) ;UpdateWindow (hwnd) ;while (GetMessage (&msg, NULL, 0, 0)){TranslateMessage (&msg) ;DispatchMessage (&msg) ;}return msg.wParam ;}LRESULT CALLBACK WndProc (HWND hwnd, UINT iMsg, WPARAM wParam, LPARAM lParam){static int cxClient, cyClient ;HDC hdc ;int i ;PAINTSTRUCT ps ;POINT pt [NUM] ;switch (iMsg){case WM_SIZE:cxClient = LOWORD (lParam) ;cyClient = HIWORD (lParam) ;return 0 ;case WM_PAINT:hdc = BeginPaint (hwnd, &ps) ;doubley[16]={500.0,363.2211,250.8730,245.2811,343.9816,399.8183,506.0272,596.9804,6 90.1846,686.1801,688.9648,550.4837,552.8629,499.4146,497.8342,500.0}; doublex[16]={500.0,500.0,506.038,269.917,264.999,268.990,346.426,388.125,405.382,466. 024,553.062,555.201,651.049,652.317,591.707,500.0};for (i = 0 ; i < 16 ; i++){pt[i].x = x[i];pt[i].y = y[i];}Polyline (hdc, pt, 16);return 0 ;case WM_DESTROY:PostQuitMessage (0) ;return 0 ;}return DefWindowProc (hwnd, iMsg, wParam, lParam) ;}C#程序:Form1:using System;using System.Collections.Generic;using ponentModel;using System.Data;using System.Drawing;using System.Linq;using System.Text;using System.Threading.Tasks;using System.Windows.Forms;using System.IO;using System.Collections.Generic;namespace导线控制网{public partial class Form1 : Form{public Form1(){InitializeComponent();}public string jisuanjieguo;public const double p = 180*3600/Math.PI;//定义角度转弧度的函数public double jiao_hu(double du,double fen,double miao){return (du*3600.0+fen*60.0+miao)/p;}//定义矩阵运算的类(包括矩阵的加、减、乘、转置和求逆)public class matrix_yusuan{//矩阵相加public static double[,] matrix_jia(double[,] Arry, double[,] Arry1) {int m = Arry.GetLength(0);int n = Arry.GetLength(1);int s = Arry1.GetLength(0);int t = Arry1.GetLength(1);double[,] temp = new double[m, n];double[,] tem = {{0}};if (m == s && n == t){for (int i = 0; i < m; i++){for (int j = 0; j < n; j++){temp[i, j] = Arry[i, j] + Arry1[i, j];}}return temp;}else{Console.WriteLine("两个矩阵大小不同");return tem ;}}//矩阵相减public static double[,] matrix_jian(double[,] Arry, double[,] Arry1) {int m = Arry.GetLength(0);int n = Arry.GetLength(1);int s = Arry1.GetLength(0);int t = Arry1.GetLength(1);double[,] temp = new double[m, n];double[,] tem = { { 0 } };if (m == s && n == t){for (int i = 0; i < m; i++){for (int j = 0; j < n; j++){temp[i, j] = Arry[i, j] - Arry1[i, j];}}return temp;}else{Console.WriteLine("两个矩阵大小不同");return tem;}}//矩阵转置public static double[,] matrix_t(double[,] Arry){int m = Arry.GetLength(0);int n = Arry.GetLength(1);double[,] temp = new double[n, m];for (int i = 0; i < n; i++){for (int j = 0; j < m; j++){temp[i,j] = Arry[j,i];}}return temp;}//矩阵相乘public static double[,] matrix_cheng(double[,] Arry, double[,] Arry1) {int m = Arry.GetLength(0);//矩阵Arry的行数int r = Arry.GetLength(1);//矩阵Arry的列数int k = Arry1.GetLength(0);//矩阵Arry的行数int n = Arry1.GetLength(1);//矩阵Arry1的列数double[,] temp = new double[m, n];double[,] tem = { { 0 } };if (r == k){for (int i = 0; i < m; i++){for (int j = 0; j < n; j++){for (int t = 0; t < r; t++){temp[i, j] += Arry[i, t] * Arry1[t, j];}}}return temp;}else{Console.WriteLine("两个矩阵无法相乘");return tem;}}//求矩阵Arry的逆矩阵public static double[,] matrix_ni(double[,] Arryni){int Level = Arryni.GetLength(1);double[,] NArry = new double[Level, Level];double HLS = matrix_yusuan.matrix_hls(Arryni);double[,] BArry = matrix_bansui(Arryni);for (int i = 0; i < Level; i++){for (int j = 0; j < Level; j++){NArry[i, j] = BArry[i, j] / HLS;}}return NArry;}//求矩阵Arry的伴随矩阵public static double[,] matrix_bansui(double[,] Arryni){int Level = Arryni.GetLength(1);double[,] BArry = new double[Level,Level];for (int m = 0; m < Level; m++){for (int n = 0; n < Level; n++){BArry[m, n] = matrix_yusuan.matrix_yuzi(Arryni, n, m);}}return BArry;}//求矩阵Arry的元素Arry[i,j]的余子式public static double matrix_yuzi(double[,] Arryni, int i, int j)//第i行,第j列,起始值为0{int Level = Arryni.GetLength(1);double[,] Arry1 = new double[Level-1,Level-1];for (int m = 0; m < Level - 1; m++){for (int n = 0; n < Level - 1; n++){if (m < i && n < j){Arry1[m, n] = Arryni[m, n];}else if(m < i && n >= j){Arry1[m, n] = Arryni[m, n + 1];}else if (m >= i && n < j){Arry1[m, n] = Arryni[m + 1, n];}else if (m >= i && n >= j){Arry1[m, n] = Arryni[m + 1, n + 1];}}}//根据矩阵元素的不同位置返回不同的值if ((i + j) % 2 != 0){return (-1)*matrix_yusuan.matrix_hls( Arry1);}else{return matrix_yusuan.matrix_hls(Arry1);}}//求行列式public static double matrix_hls(double[,] Arryni){int Level = Arryni.GetLength(1);//简单来说,对于常用的二维数组,取0或者1,分别获取列和行的长度(行数和列数)double[,] dArry = new double[Level, Level];for (int i = 0; i < Level; i++){for (int j = 0; j < Level; j++){dArry[i, j] = Arryni[i, j];}}int sign = 1;for (int i = 0, j = 0; i < Level && j < Level; i++, j++){//判断该行的正对角元素dArry[i,j]是否为0,若为0,则寻找i行以下的行m(m>i,且dArry[m,j]!=0)进行交换if (dArry[i, j] == 0){//判断是否达到了矩阵的最大行if (i == Level - 1){return 0;}int m = i + 1;//获取一个dArry[m,j]不为零的行for (; dArry[m, j] == 0; m++){if (m == Level - 1){return 0;}}//把i行和m行互换double temp;for (int n = j; n < Level; n++){temp = dArry[i, n];dArry[i, n] = dArry[m, n];dArry[m, n] = temp;}sign *= (-1);}//把当前行以下的行所对应的列变成0double tmp;//for (int s = Level - 1; s > i; s--)for (int s = i + 1; s < Level; s++){tmp = dArry[s, j];for (int t = j; t < Level; t++){dArry[s, t] -= dArry[i, t] * (tmp / dArry[i, j]); }}}double result = 1;for (int i = 0; i < Level; i++){if (dArry[i, i] != 0){result *= dArry[i, i];}else{return 0;}}return sign * result;}}public class aa//用于判断文件导入和计算是否完成{public static int panduan1 = 0;//panduan1用来判断是否进行了计算public static int panduan2 = 0;//panduan2用来判断是否导入文件}int i;int j;//定义数组double[,] hudu = new double[30, 1];double[,] bian = new double[30, 1];double[] alf = new double[30];double[] alfo = new double[30];double[] so = new double[30];double[] Xo = new double[30];double[] Yo = new double[30];double[,] B = new double[30, 27];double[,] L = new double[30, 1];double[,] P = new double[30, 30];double[,] W = new double[27, 1];double[,] temp = new double[30, 30];//此处为Xo Yo,B矩阵赋初值为零 hudu代表夹角,alf方位角,alfo方位角近似值,s 距离观测值,so距离近似值//doubleNbb[50][50],xgu[50][50],Xgu[30][1],Ygu[30][1],V[50][50],sigma_gu,Q[50][50],sigma_xy[50] [50];double[,] Nbb = new double[27, 27];double[,] xgu = new double[27, 1];double[,] xgu28 = new double[28, 1];double[,] Xgu = new double[30, 1];double[,] Ygu = new double[30, 1];double[,] V = new double[30, 1];double[,] Q = new double[27, 27];double[,] sigma_xy = new double[30, 30];double[,] sigma_xy28 = new double[30, 30];double sigma_gu;double D, F, M, sigma_hudu = 2.0, sigma_s;//用来求未知点坐标近似值private void toolStripMenuItem7_Click(object sender, EventArgs e) {if (aa.panduan1 == 1){textBox2.Text = "";textBox2.Text = "近似方位角alfo" + "\t\t" + "\r\n";for (i = 0; i < 15; i++){textBox2.Text += Math.Round(alfo[i], 6);textBox2.Text += "\r\n\r\n";}}else{MessageBox.Show("请先进行计算!", "系统提示");}}private void toolStripMenuItem10_Click(object sender, EventArgs e) {if (aa.panduan1 == 1){textBox2.Text = "";textBox2.Text = "P矩阵" + "\t\t" + "\r\n";for (i = 0; i < P.GetLength(0); i++){for (j = 0; j < P.GetLength(1); j++){textBox2.Text += Math.Round(P[i, j], 6) + "\t";}textBox2.Text += "\r\n\r\n";}}else{MessageBox.Show("请先进行计算!", "系统提示");}}private void toolStripMenuItem9_Click(object sender, EventArgs e) {if (aa.panduan1 == 1){textBox2.Text = "B矩阵" + "\t\t" + "\r\n";for (i = 0; i < B.GetLength(0); i++){for (j = 0; j < B.GetLength(1); j++){textBox2.Text += Math.Round(B[i, j], 6) + "\t";}textBox2.Text += "\r\n\r\n";}}else{MessageBox.Show("请先进行计算!", "系统提示");}}private void button15_Click(object sender, EventArgs e){if (aa.panduan2 == 1){alf[0] = Math.PI;alfo[0] = Math.PI;Xo[0] = 5000.0;Yo[0] = 5000.0;Xo[15] = 5000.0;Yo[15] = 5000.0;so[0] = bian[0, 0];for (i = 1; i < 15; i++){alf[i] = alf[i - 1] + hudu[i, 0] - Math.PI;if (alf[i] >= (2 * Math.PI)){alf[i] = alf[i] - 2 * Math.PI;}Xo[i] = Xo[i - 1] + bian[i - 1, 0] * Math.Cos(alf[i - 1]);Yo[i] = Yo[i - 1] + bian[i - 1, 0] * Math.Sin(alf[i - 1]);}jisuanjieguo += "近似距离(单位:m):" + "\r" + "近似方位角(单位:弧度):" + "\r\n";jisuanjieguo += Math.Round(so[0], 3) + "\t\t" + Math.Round(alfo[0], 6) + "\r\n";for (i = 1; i < 15; i++){//求近似距离so[i] = Math.Sqrt((Yo[i + 1] - Yo[i]) * (Yo[i + 1] - Yo[i]) + (Xo[i + 1] - Xo[i]) * (Xo[i + 1] - Xo[i]));//求近似方位角,分象限进行讨论if ((Yo[i + 1] - Yo[i]) > 0 && (Xo[i + 1] - Xo[i]) > 0)//第一象限{alfo[i] = Math.Atan((Yo[i + 1] - Yo[i]) / (Xo[i + 1] - Xo[i])); }else if ((Yo[i + 1] - Yo[i]) > 0 && (Xo[i + 1] - Xo[i]) < 0)//第二象限{alfo[i] = Math.Atan((Yo[i + 1] - Yo[i]) / (Xo[i + 1] - Xo[i])) + Math.PI;}else if ((Yo[i + 1] - Yo[i]) < 0 && (Xo[i + 1] - Xo[i]) > 0)//第三象限{alfo[i] = Math.Atan((Yo[i + 1] - Yo[i]) / (Xo[i + 1] - Xo[i])) + 2 * Math.PI;}else//((Yo[i]-Yo[i-1])<0&&(Xo[i]-Xo[i-1])<0)//第四象限{alfo[i] = Math.Atan((Yo[i + 1] - Yo[i]) / (Xo[i + 1] - Xo[i])) + Math.PI;}jisuanjieguo += Math.Round(so[i], 3) + "\t\t"+ Math.Round(alfo[i], 6) + "\r\n";}//将第一个角度的系数单独算出j = 0;//B[0][j]=0.0;((Yo[14]-Yo[0])/(so[14]*so[14]))*p/1000.0;//B[0][j+1]=0.0;-1*((Xo[14]-Xo[0])/(so[14]*so[14]))*p/1000.0;B[0, j] = -1 * (Yo[1] - Yo[0]) / (so[0] * so[0]) * p / 1000.0;//B[0][j+1]=(Xo[1]-Xo[0])/(so[0]*so[0])*p/1000.0;B[0, 25] = ((Yo[14] - Yo[0]) / (so[14] * so[14])) * p / 1000.0;B[0, 26] = -1 * (Xo[14] - Xo[0]) / (so[14] * so[14]) * p / 1000.0;//将第二个角度的系数单独算出B[1, j] = ((Yo[2] - Yo[1]) / (so[1] * so[1]) - (Yo[0] - Yo[1]) / (so[0] * so[0])) * p / 1000.0;//B[1][j+1]=-1*((Xo[2]-Xo[1])/(so[1]*so[1])-(Xo[0]-Xo[1])/(so[0]*so[0]))*p/1000.0;B[1, j + 1] = -1 * ((Yo[2] - Yo[1]) / (so[1] * so[1])) * p / 1000.0;B[1, j + 2] = ((Xo[2] - Xo[1]) / (so[1] * so[1])) * p / 1000.0;//i = i + 1;//将第三个角度的系数单独算出i = 2;B[i, j] = ((Yo[i - 1] - Yo[i]) / (so[i - 1] * so[i - 1])) * p / 1000.0;//B[i, j + 1] = -1 * ((Xo[i - 1] - Xo[i]) / (so[i - 1] * so[i - 1])) * p / 1000.0;B[i, j + 1] = ((Yo[i + 1] - Yo[i]) / (so[i] * so[i]) - (Yo[i - 1] - Yo[i]) / (so[i - 1] * so[i - 1])) * p / 1000.0;B[i, j + 2] = -1 * ((Xo[i + 1] - Xo[i]) / (so[i] * so[i]) - (Xo[i - 1] - Xo[i]) / (so[i - 1] * so[i - 1])) * p / 1000.0;B[i, j + 3] = -1 * ((Yo[i + 1] - Yo[i]) / (so[i] * so[i])) * p / 1000.0; B[i, j + 4] = (Xo[i + 1] - Xo[i]) / (so[i] * so[i]) * p / 1000.0;//求其他角度改正的系数for (i = 3; i < 15; i++){if (i < 14){B[i, j + 1] = ((Yo[i - 1] - Yo[i]) / (so[i - 1] * so[i - 1])) * p / 1000.0;B[i, j + 2] = -1 * ((Xo[i - 1] - Xo[i]) / (so[i - 1] * so[i - 1])) * p / 1000.0;B[i, j + 3] = ((Yo[i + 1] - Yo[i]) / (so[i] * so[i]) - (Yo[i - 1] - Yo[i]) / (so[i - 1] * so[i - 1])) * p / 1000.0;B[i, j + 4] = -1 * ((Xo[i + 1] - Xo[i]) / (so[i] * so[i]) - (Xo[i - 1] - Xo[i]) / (so[i - 1] * so[i - 1])) * p / 1000.0;B[i, j + 5] = -1 * ((Yo[i + 1] - Yo[i]) / (so[i] * so[i])) * p / 1000.0;B[i, j + 6] = (Xo[i + 1] - Xo[i]) / (so[i] * so[i]) * p / 1000.0; }else{B[i, j + 1] = (Yo[i - 1] - Yo[i]) / (so[i - 1] * so[i - 1]) * p / 1000.0;B[i, j + 2] = -1 * ((Xo[i - 1] - Xo[i]) / (so[i - 1] * so[i - 1])) * p / 1000.0;B[i, j + 3] = ((Yo[i + 1] - Yo[i]) / (so[i] * so[i]) - (Yo[i - 1] - Yo[i]) / (so[i - 1] * so[i - 1])) * p / 1000.0;B[i, j + 4] = -1 * ((Xo[i + 1] - Xo[i]) / (so[i] * so[i]) - (Xo[i - 1] - Xo[i]) / (so[i - 1] * so[i - 1])) * p / 1000.0;}j = j + 2;}//求边长改正的系数j = 0;//将第一个边长的系数单独算出B[i, 0] = (Xo[1] - Xo[0]) / so[0]; //(Xo[1]-Xo[0])/(so[0]*so[0]);i = i + 1;//将第二个边长的系数单独算出B[i, j] = -1 * (Xo[i - 14] - Xo[i - 15]) / so[i - 15];//B[i, j + 1] = -1 * (Yo[i - 14] - Yo[i - 15]) / so[i - 15];B[i, j + 1] = -1 * B[i, j];B[i, j + 2] = (Yo[i - 14] - Yo[i - 15]) / so[i - 15];for (i = i + 1; i < 30; i++){if (i < 29){B[i, j + 1] = -1 * (Xo[i - 14] - Xo[i - 15]) / so[i - 15];B[i, j + 2] = -1 * (Yo[i - 14] - Yo[i - 15]) / so[i - 15];B[i, j + 3] = -1 * B[i, j + 1];B[i, j + 4] = -1 * B[i, j + 2];}else{B[i, j + 1] = -1 * (Xo[i - 14] - Xo[i - 15]) / so[i - 15];B[i, j + 2] = -1 * (Yo[i - 14] - Yo[i - 15]) / so[i - 15];}j = j + 2;}jisuanjieguo += "B矩阵:" + "\r\n";for (i = 0; i < 30; i++){for (j = 0; j < 27; j++){jisuanjieguo += Math.Round(B[i, j], 6) + "\t";}jisuanjieguo += "\r\n";}//求L矩阵,角度和边长分别求解L[0, 0] = (hudu[0, 0] - (alfo[0] - alfo[14] + Math.PI)) * p;for (i = 1; i < 30; i++){if (i < 15){L[i, 0] = (hudu[i, 0] - (alfo[i] - alfo[i - 1] + Math.PI)) * p;if (L[i, 0] > Math.PI * p){L[i, 0] = (L[i, 0] - 2 * Math.PI * p);}else{L[i, 0] = L[i, 0];}}else{L[i, 0] = (bian[i - 15, 0] - so[i - 15]) * 1000.0;}}jisuanjieguo += "L矩阵(单位:秒和mm):" + "\r\n";for (i = 0; i < 30; i++){for (j = 0; j < 1; j++){jisuanjieguo += Math.Round(L[i, j], 6) + "\t\t";}jisuanjieguo += "\r\n";}//求权阵Pfor (i = 0; i < 30; i++){if (i < 15){P[i, i] = 1;}else{sigma_s = 5 + 10 * 0.000001 * bian[i - 15, 0] * 1000; //单位为(''/mm)的平方P[i, i] = sigma_hudu * sigma_hudu / (sigma_s * sigma_s);}}jisuanjieguo += "P矩阵:" + "\r\n";for (i = 0; i < 30; i++){for (j = 0; j < 30; j++){jisuanjieguo += Math.Round(P[i, j], 6) + "\t";}jisuanjieguo += "\r\n";}Nbb =matrix_yusuan.matrix_cheng(matrix_yusuan.matrix_cheng(matrix_yusuan.matrix_t(B), P), B); //计算Nbb矩阵double[,] temp2 = new double[27, 30];。
《测量平差程序》课程设计(报告)学生姓名:罗正材学号:1108030128专业:2011级测绘工程指导教师:肖东升目录一、前言 (3)二、平差程序的基本要求 (3)三、平差程序模块化 (3)图1四、平差中的重要函数(一)、角度制与弧度制的相互转化C/C++程序设计中,关于角度的计算以弧度制为单位,而在测量以及具体工作中我们通常习惯以角度制为单位。
这样,在数据处理中,经常需要在角度制与弧度制之间进行相互转化。
这里,我们利用C/C++数学函数库math.h中的相关函数完成这两种功能。
这里,我们使用double类型数据表示角度制数和弧度制数。
例如:123度44分58.445秒,用double类型表示为123.4458445,其中分、秒根据小数位确定。
在角度制与弧度制的转化中,涉及如下图2所示的两个环节。
度.分秒度弧度图21.角度化弧度函数double d_h(double angle) //角度化弧度{ double a,b;angle=modf(angle,&a);//a为提取的度值(int类型),angle为分秒值(小数)angle=modf(angle*100.0,&b); // b为提取的分值(int类型),angle为秒值(小数)return (a+b/60.0+angle/36.0)*(PI+3.0E-16)/180.0;}2.弧度化角度函数double h_d(double angle) //弧度化角度{ double a,b,c;angle=modf(angle*180.0/(PI-3.0E-16),&a);angle=modf(angle*60.0,&b);angle=modf(angle*60.0,&c);return a+b*0.01+c*0.0001+angle*0.0001;}其中,函数modf(angle,&a)为C语言数学库函数,返回值有两个,以引用类型定义的a 返回angle的整数部分,函数直接返回值为angle的小数部分。