附合导线平差程序设计报告

附合导线平差步骤一、数据处理1.数据输入：将测站、观测角度、观测距离等原始数据输入计算机或平差软件。

2.数据质检：对输入的数据进行初步的质检，检查是否存在错误数据、异常数据等，发现并剔除异常数据。

3.角度数据处理：将观测角度转换为弧度，便于后续计算。

4.距离数据处理：对观测距离进行单位转换，通常将其转换为米或千米。

5.数据配对：将同一测站观测到的角度和距离数据做配对，构成观测组。

6.编点编号：对测站进行编号，便于后续计算。

二、导线控制要素计算1.导线连杆长度计算：根据测站坐标计算导线连杆的几何长度。

2.导线初始点坐标计算：根据导线方位角、连杆长度和已知控制点的坐标计算导线初始点的坐标。

3.导线朝向角计算：根据已知控制点的坐标和导线的方位角，计算导线的朝向角。

三、平差计算1.平差模型确定：选择适当的平差模型，常用的有单位权平差模型、具有不等权的平差模型等。

2.条件方程建立：根据平差模型和导线控制要素的计算结果，建立条件方程组。

3.条件方程系数矩阵确定：根据条件方程组，将其转化为系数矩阵形式。

4.闭合差计算：根据条件方程和系数矩阵，利用最小二乘法计算闭合差，并评估其精度。

5.参数平差：利用闭合差和条件方程系数矩阵，通过参数平差法计算出导线的平差结果。

6.残差计算：根据平差结果和原始观测数据，计算各个观测量的平差残差，并评估其精度。

四、结果分析和判断1.平差结果分析：对平差结果进行查验和分析，判断平差是否满足要求，是否符合实际测量误差的范围。

2.误差判断：根据平差结果和平差残差，判断是否存在异常误差，如超限误差、粗大误差等。

3.解释和修正：对异常误差进行解释和修正，如重新检查测量数据、进行补充观测等。

以上就是附合导线平差步骤的主要内容，通过这些步骤可以得到导线的最佳平差值，为后续的工程测量提供准确的基础数据。

在实际应用中，还需根据具体情况对平差步骤进行调整和优化，以满足实际工程测量的需求。

附合导线平差计算过程说明1）道路观测左角∑β测左=308°2.'38"+70°35'41"+156°56'39"+185°39'2"+205°21'59"+174°36'43"+197°31'46"+157°36'36"+135°14'40"+167°38'50"=1759°14'34"ƒβ测=a始边- a终边=-15"。

ƒβ容=± 40√n =±126"。

ƒβ测＜ƒβ容，测角精度符合要求。

2）改正角：β=β测- ƒβ测/N。

3）坐标方位角的推算：根据起始边的坐标方位角及改正角，依据公式a下一边’= a始边+180°+转角（观测转左角）依次计算各边的坐标方位角。

4）坐标增量的计算及闭合差的调整坐标增量计算根据已经推算出的导线各边的坐标方位角和相应边的边长，按下面公式计算各边的坐标增量。

△ X AB=D AB*COS a AB，△ Y AB=D AB*SIN a AB，按附合导线要求，各边的坐标增量代数和的理论植，等于终起两点的已知坐标之差，所以，纵、横坐标增量闭合差按公式计算，Fx=∑△x测-（X终-X起）FY=∑△Y测-（Y终-Y起）导线全长闭合差f=√(ƒx2+ƒy2)=0.102m,k=f/∑D=1/38370＜1/2000.满足精度要求。

5）根据后一点的坐标及改正后的坐标增量，按公式推算前一点坐标。

X前=X后+△x改Y前=Y后+△Y改最后，推算出终止边的坐标，与原有设计值相等，以作检核。

闭合导线平差程序设计闭合导线平差程序设计1. 定义闭合导线平差是一种常用的野外测量数据处理方法，主要是对收集到的起点、中间点、终点等观测数据进行处理，以期获得精确的位置、距离等值。

2. 基本原理闭合导线平差是基于平差原理的实现，将测量起点和终点看作以相同的大小、方向的弯曲线片段组成的单一参数闭合线段进行处理，根据所取的测量观测值，以及观测变现的不确定性，经过合理的参数求解，以期尽可能准确的提取出距离、位置等变量。

3. 设计步骤利用闭合导线平差程序，实现起点和终点连接形成精确环形线段，需要包含以下几个步骤：(1) 输入测量数据：首先要搜集和输入测量数据，一般包括起点和终点的测角、距离、坐标以及各中间点的测角、距离、坐标等；(2)初始网值近似值：根据输入的测量数据，给定平差网的近似值，进行网格结构初始设置；(3)变量定义：确定变量类型，处理所有变量，根据不同的变量和变化范围，定义各种数学变量；(4)观测方程拟合：根据给定的变量，基于平差原理，拟合出符合条件及符合实际效果的观测方程；(5)历程和角度单位转换：完成测量数据的转换，将各中间点的测量数据转换为距离和角度绝对值，得到带符号角度，以方便后续数据处理；(6)主要的参数以及函数计算：根据已经获得的观测方程，求解出与之对应的函数及参数，以期获得所需要的精确结果；(7)几何和参数变换：根据主要参数和函数，进行变换和单位转换，获得をn换得整个线段的几何及参数关系；(8)最终结果输出：按照实际需求，输出最终结果，并将其保存进行下一步分析。

4. 程序优化闭合导线平差程序中有不少地方可以优化，以期获得更精准和更可靠的结果。

(1)近似值优化：数据输入时，给定的近似值尽可能的接近实际值，以期可以准确接近最终结果；(2)变量优化：确定变量类型时，按照不同改变范围和不确定性，尽可能让变量涵盖更广范围；(3)函数优化：选择合适的函数，尽可能的接近实际情况，尽心参数优化以及公式优化；(4)单位转换优化：尽量控制单位转换的正确性，以准确得出带符号角度；(5)数据输出优化：根据实际需求，输出更详细和准确的数据，以期及时发现并优化平差算法。

山西水利职业技术学院实习报告题目导线平差的程序设计与实现姓名：孟国娇学号：专业：工程造价1139报告提交日期：山西水利职业技术学院设计任务书学院：土建工程系专业年级：工程造价2011 学生姓名：孟国娇任务下达日期：2012年 2 月20日毕业设计日期：2012年3月12日至2012年6月13日毕业设计题目：导线平差的程序设计与实现毕业设计主要内容和要求：主要内容：（1）测量平差的研究背景及意义；（2）测量平差概述；（3）Excel在单一附和导线近似平差中的应用；（4）Excel在单一附和导线条件平差中的应用；（5）导线网的间接平差理论；（6）导线网平差的结构和函数设计与实现。

设计要求：（1）毕业设计要充分发挥主观能动性，积极思考，主动实践；（2）毕业设计撰写结构要严整，叙述清楚，理论分析适当，数据可靠，研究方法合理，结论正确，论文格式符合规范；（3）研究成果要有一定的实用或参考价值。

院长签字：指导教师签字：摘要随着测绘科学技术的不断发展，在测量数据的处理中产生很多种平差的方法。

在本文中，导线网的近似平差和条件平差的一些简单计算可通过Excel表编制计算公式和编程实现，我们只需在已编好的Excel表中稍作调整和公式修改，并输入已知数据，最终就可得到所需的平差结果，这为测量的内业工作提供了服务和参考；导线网的间接平差程序是利用C++编程实现的，我们需要将导线网的已知数据信息按照特定的规则输入到dat文本中，利用C++程序读取文本数据信息后，对其进行一系列的平差计算，最终获得平差后的结果，并以dat文本的形式输出且保存，这样就可为测量工作提供一定的参考，还能为测绘数据的管理带来帮助。

关键词：导线平差；Excel；C++；程序目录1绪论...............................................................................................................................................1.1研究背景及意义.................................................................................................................1.2国内外研究状况.................................................................................................................1.3本文研究的具体内容.........................................................................................................1.4平差程序相关说明.............................................................................................................1.4.1平差程序计算特点..................................................................................................1.4.2平差程序的基本要求..............................................................................................1.4.3平差程序的结构化设计..........................................................................................1.4.4平差程序模块化......................................................................................................1.4.5平差程序的数据结构.............................................................................................. 2测量平差.......................................................................................................................................2.1测量平差概述.....................................................................................................................2.1.1测量平差..................................................................................................................2.1.2测量平差的函数模型..............................................................................................2.2最小二乘原理.....................................................................................................................2.3条件平差原理.....................................................................................................................2.3.1条件平差的数学模型..............................................................................................2.3.2条件平差原理..........................................................................................................2.3.3条件平差的计算步骤..............................................................................................2.3.4精度评定..................................................................................................................2.4间接平差原理.....................................................................................................................2.4.1间接平差的数学模型..............................................................................................2.4.2间接平差的的一般原理..........................................................................................2.4.3按间接平差法求平差值的计算步骤......................................................................2.4.4精度评定.................................................................................................................. 3Excel在导线平差中的应用.........................................................................................................3.1 Excel在平差中的应用基础...............................................................................................3.1.1 引言.........................................................................................................................3.1.2Excel在平差中的基本应用操作函数...................................................................3.1.3 核心问题的解决及技巧.........................................................................................3.1.4 三角函数在Excel中的处理方法..........................................................................3.1.5 小结.........................................................................................................................3.2Excel在附和导线近似平差中的应用..............................................................................3.2.1 单一附和导线近似平差.........................................................................................3.2.2单一附和导线近似平差实例..................................................................................3.3 Excel在导线网条件平差中的应用...................................................................................3.3.1单一附合导线条件平差..........................................................................................3.3.2边角权的确定及单位权中误差..............................................................................3.3.3单一附和导线条件平差实例.................................................................................. 4导线网的间接平差程序设计与实现 ...........................................................................................4.1矩阵的相关函数.................................................................................................................4.1.1矩阵相乘..................................................................................................................4.1.2矩阵转置..................................................................................................................4.1.3矩阵求逆..................................................................................................................4.1.4矩阵输出..................................................................................................................4.1.5设置实数输出精度..................................................................................................4.2平差中的重要函数.............................................................................................................4.2.1角度制与弧度制的相互转化..................................................................................4.2.2测量正反算函数......................................................................................................4.2.3近似坐标计算..........................................................................................................4.3导线网的平差理论.............................................................................................................4.3.1平差概述..................................................................................................................4.3.2边角网的最小二乘平差..........................................................................................4.4间接平差的结构与函数设计.............................................................................................4.4.1间接平差..................................................................................................................4.4.2结构与函数设计......................................................................................................4.5导线网平差的程序应用.....................................................................................................4.5.1平面网数据的输入格式..........................................................................................4.5.2导线网平差程序应用实例...................................................................................... 5结论与展望 ...................................................................................................................................5.1Excel在导线平差中的应用..............................................................................................5.1.1Excel在导线近似平差中的应用...........................................................................5.1.2Excel在导线网条件平差中的应用.......................................................................5.2C++在导线平差中的应用 .................................................................................................5.3测量平差的展望................................................................................................................ 参考文献........................................................................................................................................... 致谢. (54)1绪论1.1研究背景及意义测量工作是工程施工非常基础、重要的环节，对工程设计、工程施工、工程的验收都发挥着指导性、不可替代的作用。

附和导线平差计算详细教程，留着慢慢学习！本篇继续讲解附和导线的内业平差。

平差顾名思义就是把总误差进行平均分配，让每个点的误差都控制在允许的范围内。

平差有两种方式，一是手动平差，二是软件平差。

本文讲解手动平差，这个过程能让新手测量员们掌握平差的原理，和相关的基础知识。

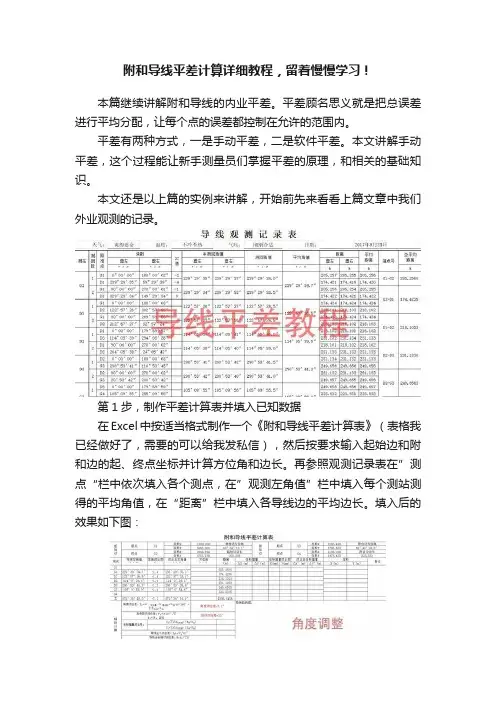
本文还是以上篇的实例来讲解，开始前先来看看上篇文章中我们外业观测的记录。

第1步，制作平差计算表并填入已知数据在Excel中按适当格式制作一个《附和导线平差计算表》（表格我已经做好了，需要的可以给我发私信），然后按要求输入起始边和附和边的起、终点坐标并计算方位角和边长。

再参照观测记录表在”测点“栏中依次填入各个测点，在”观测左角值”栏中填入每个测站测得的平均角值，在“距离”栏中填入各导线边的平均边长。

填入后的效果如下图：注：已知边的方位角和边长的计算方式很多，比如用5800计算器的Pol函数，道路之星的测站、CASS查询等。

第2步，计算角度闭合差计算角度闭合差，是为了检验外业角度观测的精度是否满足相应等级导线的技术要求。

如果实测的角度闭合差<>相关计算公式：实测角度闭合差=实测附和边方位角-理论附和边方位角实测附和边方位角=起始边方位角-N*180+实测左角值之和容许角度闭合差各等级导线有相应规定（各等级导线的技术要求在上篇文章中）。

注：N为测量站数，方位角取值范围是0度（含）到360度（不含），大于360度的减去360度，小于0度的加上360度。

本案例经计算：角度闭合差=7.1秒，容许闭合差=22秒，观测精度合格。

第3步，计算左角改正数经过角度闭合差的计算，确定外业成果合格后，就要计算左角改正数。

左角改正数=角度闭合差的相反数/测站个数改正后左角值=观测左角值+左角改正数本案例角度闭合差=7.1秒，那么左角改正数=-7.1/5=-1.42秒。

分配说明：为尽量平均分配误差，我们可将改正数保留1位小数，所以案例中每个测站分配-1.4秒，这时还有0.1秒未得到分配。

一、实验目的本次实验旨在使学生了解和掌握导线平差的基本原理和方法，通过实际操作，培养学生运用数学模型解决实际问题的能力，提高学生在测绘工程中的实际操作技能。

二、实验原理导线平差是测量数据处理的一种方法，通过调整观测值，使平差后的观测值与实际观测值尽可能接近。

实验中，我们主要采用最小二乘法进行导线平差，该方法的基本原理是：在最小二乘法中，误差平方和为最小，即：\[ S = \sum_{i=1}^{n} (L_i - L_{\text{平差}})^2 \]其中，\( L_i \)为第\( i \)个观测值，\( L_{\text{平差}} \)为平差后的观测值。

三、实验仪器与材料1. 全站仪一台2. 导线测量记录簿3. 计算器4. 导线平差计算软件四、实验步骤1. 测量数据采集（1）将全站仪安置在已知点A上，对B、C、D、E等点进行观测，记录观测数据。

（2）按照测回法进行水平角观测，记录观测数据。

（3）对导线各边进行水平边长观测，记录观测数据。

2. 数据整理（1）将观测数据输入导线平差计算软件。

（2）对数据进行整理，包括角度换算、坐标转换等。

3. 平差计算（1）设置平差参数，如权系数、改正数等。

（2）进行平差计算，得到平差后的观测值。

4. 结果分析（1）分析平差后的观测值与实际观测值的差异。

（2）根据差异，调整平差参数，提高平差精度。

五、实验结果通过实验，我们得到了以下结果：1. 平差后的观测值与实际观测值的差异较小，说明平差效果较好。

2. 通过调整平差参数，可以进一步提高平差精度。

六、实验总结本次实验使我们深入了解了导线平差的基本原理和方法，掌握了导线平差计算步骤。

通过实际操作，我们提高了运用数学模型解决实际问题的能力，为今后的测绘工作打下了基础。

七、实验心得1. 导线平差是测量数据处理的重要方法，对于提高测量精度具有重要意义。

2. 在实验过程中，要注意数据整理和平差参数的设置，以确保实验结果的准确性。

《测量平差程序》课程设计（报告）学生姓名：罗正材学号：1108030128专业：2011级测绘工程指导教师：肖东升目录一、前言 (3)二、平差程序的基本要求 (3)三、平差程序模块化 (3)图1四、平差中的重要函数（一）、角度制与弧度制的相互转化C/C++程序设计中，关于角度的计算以弧度制为单位，而在测量以及具体工作中我们通常习惯以角度制为单位。

这样，在数据处理中，经常需要在角度制与弧度制之间进行相互转化。

这里，我们利用C/C++数学函数库math.h中的相关函数完成这两种功能。

这里，我们使用double类型数据表示角度制数和弧度制数。

例如：123度44分58.445秒，用double类型表示为123.4458445，其中分、秒根据小数位确定。

在角度制与弧度制的转化中，涉及如下图2所示的两个环节。

度.分秒度弧度图21.角度化弧度函数double d_h(double angle) //角度化弧度{ double a,b;angle=modf(angle,&a);//a为提取的度值（int类型），angle为分秒值（小数）angle=modf(angle*100.0,&b); // b为提取的分值（int类型），angle为秒值（小数）return (a+b/60.0+angle/36.0)*(PI+3.0E-16)/180.0;}2.弧度化角度函数double h_d(double angle) //弧度化角度{ double a,b,c;angle=modf(angle*180.0/(PI-3.0E-16),&a);angle=modf(angle*60.0,&b);angle=modf(angle*60.0,&c);return a+b*0.01+c*0.0001+angle*0.0001;}其中，函数modf(angle,&a)为C语言数学库函数，返回值有两个，以引用类型定义的a 返回angle的整数部分，函数直接返回值为angle的小数部分。

附合导线严密平差算法总结图1如图的单一附合导线，有4个已知点A、B、C、D，2个未知点TP1、TP2。

设观测边数为n, 则未知点数为n-1, 观测角数为n+1。

以上图为例，n = 3。

观测边为：S1 = B->TP1,S2 = TP1->TP2, S3 = TP2->C思路：由于A、B坐标已知，则可以算出起始方位角，再根据B点坐标和每个观测角（夹角，左角）推算出TP1、TP2、C点的近似坐标值。

如果是用全站仪进行测量，则用盘左盘右重复观测求平均的方式，直接测出TP1、TP2、C点的近似坐标值以及CD的方位角。

再根据c点的已知坐标与近似坐标求坐标闭合差，由CD的已知方位角和近似方位角求角度闭合差，两个闭合差联立求得边长和角度的改正数，最后求得未知点的坐标平差值。

条件平差过程：1.建立条件方程，求得条件系数2.求法方程系数3.求权阵4.计算出联系数K5.解算出观测值改正数V6.由观测值和改正数计算平差值详细步骤如下：1、建立条件方程在单一附合导线中，只需要三个条件方程即：方位角附合条件、纵坐标附合条件和横坐标附合条件方程。

（省略了条件方程的推导过程，详细过程请查看参考资料：《测量平差.pps》）（1）方位角附合条件[Vβi]n+11+ Wβ= 0式中，Wβ= - （T0– T CD+ [βi]n+11 - （n+1）*180°）（角度闭合差）βi ——角度观测值（夹角，左角）Vβi ——各观测角的改正数。

如果是用全站仪观测，则Wβ= - （T CD– T CD）式中，T CD ——CD的方位角观测值，T CD ——CD的已知方位角（2）纵坐标X附合条件方程[Cos TI * VSi]1n - （1/ ρ”）* [(Yn+1- Yi) * Vβi]1n - W x = 0;式中，TI——各方位角观测值（近似值）VSi——边长改正数Yn+1—— C点即终止点的横坐标Y的观测值（近似值）Yi——待定点的横坐标Y的观测值Wx = - （Xn+1- XC）XC—— C点即终止点的纵坐标X的已知值ρ” = 2062.65（3）横坐标Y附合条件方程[Sin TI * VSi]1n + （1/ ρ”）* [(Xn+1- Xi) * Vβi]1n– W Y = 0;式中，TI——各方位角观测值（近似值）VSi——边长改正数Xn+1—— C点即终止点的纵坐标X的观测值（近似值）Xi——待定点的纵坐标X的观测值WX = - （Yn+1- YC）YC—— C点即终止点的横坐标Y的已知值ρ” = 2062.652、求条件方程的系数矩阵联立3个方程得改正数条件方程组：[Vβi]n+11+ Wβ= 0[Cos TI * VSi]1n - 1/ ρ”* [(Yn+1- Yi) * Vβi]1n - W x = 0;[Sin TI * VSi]1n + 1/ ρ”* [(Xn+1- Xi) * Vβi]1n– W Y = 0;其系数矩阵arrA为：（即改正数V的系数，此处以图1为例， n = 3）3、联系数法方程（简称法方程）AP-1A T K – W = 0A——系数矩阵arrAK ——乘系数P ——权阵W ——闭合差矩阵由上得法方程的系数阵N：N = AP-1A T（权的推导见参考资料：《全站仪观测导线测量平差方法的研究.pdf》）角度权：P βi = 1；（因为角度的标称精度是固定的，各观测角权值相等） 边长权：P Si = (μ0 *μ0 ) / （M D * M D ）（误差比例系数固定，边长的误差与距离有关，因此不一致）式中，μ0 ——先验测角中误差，以秒为单位 M D —— 距离观测中误差若 导线边长为S i （米），e1 为仪器的边长标称固定误差（mm ），e2为仪器的边长比例误差系数（无单位），则M D = ± （e1 + e2 * S i * 0.001）mm 需转化为厘米：M D = M D ** 0.1 （cm ）由于此处是要P 的逆矩阵P -1,因此要求P 的各元素的倒数（P 是对角矩阵，对角矩阵的逆矩阵就是原矩阵元素的倒数） Psi = 1/ Psi ；由上可得，P -1 矩阵如下：4、求改正数由于N 已经在前面的步骤中求出，求N 的逆矩阵。

导线网平差程序设计报告1. 引言在工程测量中，导线网平差是一项重要的任务，其目的是通过测量数据的处理，求取已测量量的最优估计值，并得出测量结果的可信度。

导线网平差程序设计是实现这个过程的关键步骤之一。

本报告将介绍导线网平差程序的设计过程，并详细说明设计的原理、算法和实现细节。

2. 设计原理导线网平差程序的设计原理基于最小二乘法。

最小二乘法是一种通过最小化观测结果与理论模型的残差平方和来估计模型参数的数学方法。

在导线网平差中，我们可以将每个观测值看作是理论值与测量误差的和，以此建立观测方程。

通过最小二乘法，可以求解出观测量的最优估计值。

3. 算法设计3.1. 数据输入导线网平差程序首先需要获取测量数据。

这些数据可能包括导线的起始点和终止点坐标、导线的观测距离和导线的观测方向等。

程序需要能够读取这些数据，并将其存储在内存中以供后续处理。

3.2. 创建观测方程根据测量数据，程序需要创建观测方程。

观测方程可以使用矩阵形式表示，其中每个元素对应一个测量值。

观测方程的建立需要依据测量理论和导线网的具体结构。

3.3. 计算平差数值解通过最小二乘法，可以计算出导线网平差的数值解。

数值解是观测量的最优估计值，可以考虑加权或限制条件等问题。

3.4. 计算平差结果通过平差数值解，可以计算出每个测量值的平差结果。

这些结果可以包括平差坐标、观测误差、精度估计等。

3.5. 输出结果最后，程序需要将平差结果输出到文件或打印屏幕上，以便用户查看和使用。

4. 实现细节为了设计一个高效且易于使用的导线网平差程序，我们可以选择使用编程语言来实现。

常见的编程语言有Python、C++等。

在程序实现过程中，我们可以使用一些常用的库和工具来简化开发过程，例如NumPy和SciPy用于矩阵计算，matplotlib用于结果可视化等。

在实现中，我们需要设计合适的数据结构来存储测量数据和计算结果，例如使用数组、矩阵或自定义的数据结构。

5. 结论导线网平差程序的设计是一个复杂而重要的任务。

附合导线按条件平差算例9.4.1附合导线的条件平差方程式如图9-6所示，符合在已知),(A A y x A ，),(C C y x C 之间的单一符合导线有n 条AB α与CDα是已知方位角。

设观测角为β、β、… …、β，测角中误差为 ，观测边长为s 、s 、… …、s ，故t1为v 1=ii BACD 011=+∑+=a i n i v ω （9-2）式中a ω—方位角条件的不符值，按180)1(ˆ11+-∑+-=+=n in i CD BAaβααω （9-3）若导线的A 点与C 点重合，则形成一闭合导线，由此坐标方位角条件就成了多边形的图形闭合条件。

2、纵、横坐标条件 设以1ˆx ∆、2ˆx ∆、…、n x ˆ∆表示图中各导线边的纵坐标增量之平差值；1ˆy∆、2y ∆、…、n yˆ∆表示图中各导线边的横坐标增量之平差值；由图可写出以坐标增量平差值表示的纵、横坐标条件。

⎪⎪⎭⎪⎪⎬⎫∑+∆∑+=∆∑+=∑+∆∑+=∆∑+=∆∆yi n i n A i n A C xi n i n A i nA C v y y yy y v x x xx x 111111ˆˆ （9-4）σ令⎪⎪⎭⎪⎪⎬⎫--∆∑=--∆∑=)()(11A Ci nyA C i nx y y y x x x ωω （9-5）则⎪⎪⎭⎪⎪⎬⎫=+∑=+∑∆∆0011yyi nx xi nv v ωω （9-6） 以微分量代替改正数，则有)()()(211n xi nx d x d x d v ∆++∆+∆=∑∆{}ρα1231211)()()(cos v y y y y y y v v n Csi i nxin-'++-+--∑=∑∆将上式代入式9-6得纵坐标条件式，且同理已可得横坐标的条件式即⎪⎪⎭⎪⎪⎬⎫=+-'∑+∑=+-'∑-∑====0)(1sin 0)(1cos 1111y i i Cni sii n i x i i Cni si i n i v x x v v y y v ωραωρα （9-7）上式就是单一符合导线的纵、横坐标条件方程x ω、y ω为条件式的不符值，按⎪⎪⎭⎪⎪⎬⎫-'=-∆∑+=-'=-∆∑+=C CCi nA yC CC i nA x y y y y y x x x x x 11ωω （9-8）式中i x 、i y 是由观测值计算的各导线点的近似坐标。

附和导线近似平差计算程序P:A:B:I:J:K:L:Defm12 P=P+2:N=0:M=AW=60√P÷3600LbI0N=N+1{C}Z[2N-1]=C:M=M+CM>180=>M=M-180:≠=>M=M+180⊿N<P=>Goto0⊿F=M-B:F>360=>F=F-360⊿F▲AbsF<W=>F=-F÷P:≠=>Goto E⊿N=0:M=ALbI1N=N+1:M=M+Z[2N-1]+FM>180=>M=M-180▲≠=>M=M+180▲⊿Z[2N-1]=MN<P=>Goto1⊿N=0:M=0:G=0:H=0:P=P-1LbI2N=N+1{D}:Z[2N]=D:M=M+DX=DcosZ[2N-1]:Y=DsinZ[2N-1]G=G+X:H=H+YZ[2N-1]=X:Z[2N]=YN<P=>Goto2⊿G=G+I-K▲H=H+J-L▲T=√(G×G+H×H)▲Q=M÷T▲Q>2000=>G=-G÷M:H=-H÷M:≠=>Goto E⊿N=0:X=I:Y=JLbI3N=N+1▲D=√(Z[2N-1]×[2N-1]+Z[2N]×[2N])V=Z[2N-1]+DG▲U=Z[2N]+DH▲X=X+V▲Y=Y+U▲Z[2N-1]=X:Z[2N]=YN<P=>Goto3⊿LbI E说明:1程序中Defm12是按4个未知点设置的,计算时要进行修改。

如未知点数为n,修改数为2(n+2)。

1:P输入未知点数2:A输入起点方位角3:输入终点方位角4:I,J输入起点坐标5:K,L输入终点坐标6:C从导线起点依次观测角7:F角度闭合差8:M导线第一边依次方位角平差值9:D导线第一边依次输边长10:G,H为(⊿X,⊿Y)导线闭合差11:T为导线绝对误差12:Q为导线相对闭合差分母,分子为1 13:N导线未知点数14:V,U为导线第一边坐标增量平差值15:X,Y为导线未知点坐标平差值。

附合导线平差计算过程说明1）道路观测左角∑β测左=308°2.'38"+70°35'41"+156°56'39"+185°39'2"+205°21'59"+174°36'43"+197°31'46"+157°36'36"+135°14'40"+167°38'50"=1759°14'34"ƒβ测=a始边- a终边=-15"。

ƒβ容=± 40√n =±126"。

ƒβ测＜ƒβ容，测角精度符合要求。

2）改正角：β=β测- ƒβ测/N。

3）坐标方位角的推算：根据起始边的坐标方位角及改正角，依据公式a下一边’= a始边+180°+转角（观测转左角）依次计算各边的坐标方位角。

4）坐标增量的计算及闭合差的调整坐标增量计算根据已经推算出的导线各边的坐标方位角和相应边的边长，按下面公式计算各边的坐标增量。

△ X AB=D AB*COS a AB，△ Y AB=D AB*SIN a AB，按附合导线要求，各边的坐标增量代数和的理论植，等于终起两点的已知坐标之差，所以，纵、横坐标增量闭合差按公式计算，Fx=∑△x测-（X终-X起）FY=∑△Y测-（Y终-Y起）导线全长闭合差f=√(ƒx2+ƒy2)=0.102m,k=f/∑D=1/38370＜1/2000.满足精度要求。

5）根据后一点的坐标及改正后的坐标增量，按公式推算前一点坐标。

X前=X后+△x改Y前=Y后+△Y改最后，推算出终止边的坐标，与原有设计值相等，以作检核。

三、导线测量的外业工作CAD、CASS、纬地语言编程、excel VBA语言编程、VB可视化编程、主流软件的使用（如：CAD、CASS、纬地等），其次更需要明确测量的内涵。

（一）踏勘选点选点就是在测区内选定控制点的位置。

选点之前应收集测区已有地形图和高一级控制点的成果资料。

根据测图要求，确定导线的等级、形式、布置方案。

在地形图上拟定导线初步布设方案，再到实地踏勘，选定导线点的位置。

若测区范围内无可供参考的地形图时，通过踏勘，根据测区范围、地形条件直接在实地拟定导线布设方案，选定导线的位置。

导线点点位选择必须注意以下几个方面：1、为了方便测角，相邻导线点间要通视良好，视线远离障碍物，保证成像清晰。

2、采用光电测距仪测边长，导线边应离开强电磁场和发热体的干扰，测线上不应有树枝、电线等障碍物。

四等级以上的测线，应离开地面或障碍物1.3 以上。

3、导线点应埋在地面坚实、不易被破坏处，一般应埋设标石。

4、导线点要有一定的密度，以便控制整个测区。

5、导线边长要大致相等，不能悬殊过大。

导线点埋设后，要在桩上用红油漆写明点名、编号，并用红油漆在固定地物上画一箭头指向导线点并绘制“点之记”方便寻找导线点，如图6-5所示。

（一）踏勘选点选点就是在测区内选定控制点的位置。

选点之前应收集测区已有地形图和高一级控制点的成果资料。

根据测图要求，确定导线的等级、形式、布置方案。

在地形图上拟定导线初步布设方案，再到实地踏勘，选定导线点的位置。

若测区范围内无可供参考的地形图时，通过踏勘，根据测区范围、地形条件直接在实地拟定导线布设方案，选定导线的位置。

导线点点位选择必须注意以下几个方面：1、为了方便测角，相邻导线点间要通视良好，视线远离障碍物，保证成像清晰。

2、采用光电测距仪测边长，导线边应离开强电磁场和发热体的干扰，测线上不应有树枝、电线等障碍物。

四等级以上的测线，应离开地面或障碍物1.3 以上。

3、导线点应埋在地面坚实、不易被破坏处，一般应埋设标石。

具有后验方差检验评价功能的附合导线平差程序附合导线平差是测量工程中常用的一种技术，用于对导线的观测数据进行处理和评价。

附合导线平差程序是用来实现附合导线平差的计算程序。

在附合导线平差程序中，后验方差检验评价功能是非常重要的，可以用来评估平差结果的精度和可靠性。

下面将介绍一种具有后验方差检验评价功能的附合导线平差程序的设计思路。

该附合导线平差程序的设计包括以下几个主要步骤：1.数据输入：程序首先要求用户输入初始观测数据，包括每个导线的起点、终点坐标、观测的距离和高差。

导线的观测数据应按照一定的格式进行输入，可以支持导入外部文本文件或手动输入。

2.参数计算：程序根据输入的观测数据，计算每个导线的长度、倾斜角和方位角。

计算方法可以采用三角法或其他几何计算方法。

3.附合导线计算：根据导线的倾斜角和方位角，利用附合导线平差公式计算导线的坐标。

计算结果会得到每个导线的中间点坐标。

4.误差传播计算：根据已知导线的坐标和观测数据的精度，利用误差传播公式计算每个导线的坐标误差值。

计算结果会得到每个导线的坐标误差。

5.后验方差计算：利用计算得到的坐标误差，利用后验方差公式计算每个导线的坐标后验方差。

计算结果会得到每个导线的坐标后验方差。

6.后验方差检验评价：根据后验方差的计算结果，进行后验方差检验评价。

该评价可以基于一定的标准或规范，比如根据误差椭圆的形状、面积、长轴、短轴等指标进行评价。

7.结果输出：将计算和评价结果进行输出，可以以文本形式或图形形式展示。

输出结果应包括每个导线的坐标、坐标误差、坐标后验方差，以及后验方差的检验评价结果。

8.可视化展示：可以通过绘制误差椭圆、误差图表等方式，对计算结果进行可视化展示，以便用户更直观地了解平差结果的精度和可靠性。

以上是一种具有后验方差检验评价功能的附合导线平差程序的设计思路。

在程序的实现中，可以根据具体需求和条件，选择适当的算法和数学模型来进行计算和评价。

同时，还可以根据实际应用需求，进行进一步的功能扩展，比如支持多种不同的后验方差计算方法、更丰富的评价指标等。

观测角度形式角度改正数改正后角度方位角度形式边长D°′″°″°°′″°m A D∑109650241096.84665.38相对中误差=F D ∶∑S =1∶2188.22说明：1、表中红色数据为观测值；蓝色数据为已知值；绿色数据为角度、方位角以度（不以度分秒）的表达形式，会自动计2、C19和D19处的数字不能为负或大于60，K列数字不能为负或大于360，否则需人工处理。

测量：记录：计算：审核：4C 27843122125230B 1292175156方位角α180.7322230.3706206.8761202.3833203.115631804354角度观测值（左角）点号31752630243063018180.731667222292.5016667156.505175.506667精度分析附合导线平差计算程序278.72212.87522278.7206212.8756175.507292.50222156.50563344242317.8683133.84154.7180.74148.93301.8361334.7117147.16ΔxΔyυxυyΔx′Δy′xy-357.369-387.255-0.13071-0.27455秒）的表达形式，会自动计算，可隐藏；紫色数据为平差结果。

-137.00277.59672日期：-125.021-0.02926-0.02891-58.5294-125.082-0.06145-0.060723802.8514006.77-70.00253903.6333805.1083833.6313943.138-103.137-30.77924028.533730.436坐标增量计算值(m)坐标增量改正数（m)改正后的坐标增量（m)坐标(m)-0.05522-0.06384-0.03331-0.02629-0.03039-85.3658程序-0.01586-85.3921-138.03-74.6727-103.082-69.9386-30.7459-137.999-74.6568-136.9733671.033619.243593.4333744.32277.62563-58.468。

导线平差实验报告1. 实验目的导线平差实验是为了确定长导线的精确长度和形状，以及测量误差的大小。

本实验旨在通过平差法对一条导线进行精确的长度测量和误差分析，以验证平差法的准确性和可靠性。

2. 实验原理导线平差是一种基于数学原理的测量方法，用于求解导线的精确长度和坐标。

在导线平差过程中，通过在不同位置测量导线的坐标，以及测量噪声和环境因素等，校正和修正测量误差，从而得到更精确的测量结果。

导线平差一般包括以下几个步骤：1. 测量导线的坐标：在导线上选择若干测量点，使用全站仪或其他测量仪器进行测量，记录对应的坐标值。

2. 进行精确导线长测量：通过对测量点进行精确测量，使用导线计或其他精密测量工具，测量导线的实际长度，得到真值。

3. 分析和修正误差：根据实际测量值和测量点的坐标，计算出各测量线的长度和角度，使用平差法或其他数学方法，对测量误差进行分析，并进行修正。

4. 计算导线的最终长度：根据修正后的测量数据，计算出导线的最终长度和形状。

3. 实验步骤1. 在实验室内准备全站仪、计算机及相关软件，并确保设备的准确性和稳定性。

2. 在实验场地选择一段长度适中的导线段，放置在水平平台上，并使用全站仪进行测量，记录下各个测量点的坐标。

3. 对选定的导线段进行精确长度测量，使用导线计进行测量，并记录测量结果。

4. 使用测量数据，进行导线的平差计算。

根据测量点的坐标和距离，计算各测量线的长度和角度，并进行误差分析和修正。

5. 根据修正后的测量数据，计算导线的最终长度和形状，并将结果整理和输出。

4. 实验结果经过测量和平差计算，得到以下结果：- 导线总长度为：100.5米- 最大误差不超过：0.01米- 导线形状为：直线5. 实验分析与结论通过导线平差实验，我们得到了导线的精确长度和形状，并分析了测量误差的大小及影响因素。

根据实验结果，我们可以得出以下结论：1. 导线平差法能够精确测量导线的长度和形状，且结果较为可靠。

5 附合导线计算程序设计#include<stdio.h>#define PI 3.1415926#include<math.h>#define LEN sizeof(struct node)#include<stdlib.h>struct zuobiao{double x;double y;};struct angle{int degree;int minute;float second;};struct node{double x;double y;struct angle ang1;struct angle fwj;double s;double dx;double dy;struct node *next;};double jtod(struct angle jiao){double degree;degree=jiao.degree;degree+=(jiao.minute/60.0);degree+=(jiao.second/3600.0);return degree;}struct angle dtoj(double jiaodu){struct angle fwj;fwj.degree=floor(jiaodu);fwj.minute =floor((jiaodu-floor(jiaodu))*60);fwj.second =((jiaodu-floor(jiaodu))*60-fwj.minute)*60;return fwj;}double jtoh(struct angle jiaodu){double hu;hu=jtod(jiaodu);hu=hu*PI/180;return hu;}main(){FILE *fp;struct zuobiao zb0,zbN;struct node *head,*p1,*p2;struct angle angle1,f0,fB,fN;int n,i;double t,fBsecond,jiaodu;double fX=0,fY=0,K=0,S=0;fB.degree=0;fB.minute=0;fB.second=0;if((fp=fopen("d:\\pro\\data2.txt","r"))==NULL)printf("cannot open this file\n");fscanf(fp,"%d",&n);fscanf(fp,"%lf%lf",&zb0.x,&zb0.y);fscanf(fp,"%d%d%f",&f0.degree,&f0.minute,&f0.second);fscanf(fp,"%lf%lf",&zbN.x,&zbN.y);fscanf(fp,"%d%d%f",&fN.degree,&fN.minute,&fN.second);fB.degree=f0.degree;fB.minute=f0.minute;fB.second=f0.second;fBsecond=jtod(fB);for(i=0;i<n;i++){fscanf(fp,"%d%d%f",&angle1.degree,&angle1.minute,&angle1.second);fBsecond+=jtod(angle1);fBsecond-=180;if(fBsecond>360) fBsecond-=360;if(fBsecond<0) fBsecond+=360;}fBsecond-=jtod(fN);fBsecond*=3600;printf("%lf\n",fBsecond);fBsecond/=-n;rewind(fp);for(i=0;i<11;i++) fscanf(fp,"%lf",&t);head=p1=p2=(struct node *)malloc(LEN);//fscanf(fp,"%d%d%f",&p1->fwj.degree ,&p1->fwj.minute ,&p1->fwj.second ); for(i=0;i<n;i++){fscanf(fp,"%d%d%f",&p1->ang1.degree ,&p1->ang1.minute ,&p1->ang1.second );p1->ang1.second +=fBsecond;if(p1->ang1.second >=60){p1->ang1.second -=60;p1->ang1.minute +=1;if(p1->ang1.minute >=60){p1->ang1.minute -=60;p1->ang1.degree +=1;}}if(p1->ang1.second <0){p1->ang1.second +=60;p1->ang1.minute -=1;if(p1->ang1.minute <0){p1->ang1.minute +=60;p1->ang1.degree -=1;}}p2->next =p1;p2=p1;p1=(struct node *)malloc(LEN);}p2->next=NULL;p1=head;i=0;do{fscanf(fp,"%lf",&p1->s);printf("s[%d]=%.3lf m\n",i+1,p1->s);S+=p1->s;i++;p1=p1->next ;}while(p1->next!=NULL);p1->s=0;printf("S=%8.3lf m\n",S);p1=head;//p1->dx=p1->s*cos(jtoh(p1->fwj ));//p1->dy=p1->s*sin(jtoh(p1->fwj ));//p1=p1->next;jiaodu=jtod(f0);do{jiaodu+=jtod(p1->ang1);jiaodu-=180;if(jiaodu>360) jiaodu-=360;if(jiaodu<0) jiaodu+=360;p1->fwj =dtoj(jiaodu);p1->dx=p1->s*cos(jtoh(p1->fwj));p1->dy=p1->s*sin(jtoh(p1->fwj));p1=p1->next ;}while(p1->next !=NULL);p1=head;fX=zb0.x;fY=zb0.y;do{fX+=p1->dx;fY+=p1->dy;p1=p1->next ;}while(p1->next !=NULL);fX-=zbN.x;fY-=zbN.y;K=sqrt(fX*fX+fY*fY);K/=S;K=1/K;p1=head;if(K>4000){do{// p2=p1->next ;p1->dx+=(-fX/S*p1->s);// p2->x=p1->x+p2->dx;p1->dy+=(-fY/S*p1->s);// p2->y=p1->y+p1->dy;p1=p1->next ;}while(p1->next !=NULL);p1=head;p1->x=zb0.x+p1->dx;p1->y=zb0.y+p1->dy;do{p2=p1->next;p2->x=p1->x+p2->dx;p2->y=p1->y+p2->dy;p1=p1->next ;}while(p2->next !=NULL);}else printf("the error is out of the limite!"),exit(0);printf("fX=%6.3lfm fY=%6.3lfm fS=%6.3lfm K=1 / %d\n",fX,fY,sqrt(fX*fX+fY*fY),(int)K);p1=head;do{printf("%8.3lf %8.3lf\n",p1->x,p1->y);p1=p1->next;}while(p1->next !=NULL);fclose(fp);if((fp=fopen("d:\\pro\\coordinate.dat","w"))==NULL)printf("cannot open this file!\n");fprintf(fp,"fx=%.3lf m\n",fX);fprintf(fp,"fy=%.3lf m\n",fY);fprintf(fp,"fs=%.3lf m\n",sqrt(fX*fX+fY*fY));fprintf(fp,"K=1 / %d\n",(int)K);fprintf(fp,"The coordinates are(m):\n");p1=head;fprintf(fp,"[1]%8.3lf %8.3lf\n",zb0.x,zb0.y);i=1;do{fprintf(fp,"[%d]%8.3lf %8.3lf\n",i+1,p1->x,p1->y);i++;p1=p1->next;}while(p1->next !=NULL);fclose(fp);}。

测量程序设计实习报告目录一、实习目的 (3)二、实习任务 (3)三、实习时间、地点、指导老师 (3)四、实习过程 (3)五、实习中主要技术问题及处理方法 (6)六、实习收获及感想 (9)七、意见及建议 (9)一、实习目的在实践中综合应用第一学年中课堂所学的计算机知识，以期能够熟练掌握基本编程语法、程序设计思想，为后续课程打下基础。

1．深入理解面向对象编程思想，理解对象的封装、继承及多态的含义；2．掌握一门高级编程语言（可选VC++，Borland C++Builder，Visual Basic或Delphi）和程序调试一般方法和技巧，熟练运用集成编程环境的基本功能，了解编程帮助系统；3．掌握基本的类模块设计与实现、数据结构、数据文件读写、人机界面设计等；4．综合运用所学数学和专业相关知识，设计并实现若干个类；5．养成良好的编程风格。

二、实习任务1．根据面向对象思想完成角度处理类模块2．根据面向对象思想完成解析交会点位坐标计算类模块3．根据面向对象思想完成附合导线近似坐标计算类模块4．测量程序设计三、实习时间、地点、指导老师时间：2013年7月6日～7月15日地点：犀浦校区X4245机房指导老师：黄泽纯四、实习过程7月6日～7日1．了解面向对象程序设计思想1）类的基本概念；2）类的成员函数添加、定义方法；3）访问对象成员方法。

2．编写角度处理类函数代码1）建立角度处理类命名DegSwitch；2）角度值转换成度分秒函数命名Deg_DMS；3）度分秒转换成角度值函数命名DMS_Deg；4）角度值转换成弧度值函数命名Deg_Rad；5）弧度值转换成角度值函数命名Rad_Deg；6）弧度值转换成度分秒函数命名Rad_DMS；7）度分秒转换成弧度值函数命名DMS_Rad；8）坐标方位角反算函数命名C_A。

3．角度处理类函数调用、算法检查及修改1）函数调用方法：指针；2）主函数中选择调用函数关键语句：switch语句。