扭转典型习题解析
- 格式:pdf
- 大小:306.90 KB
- 文档页数:8
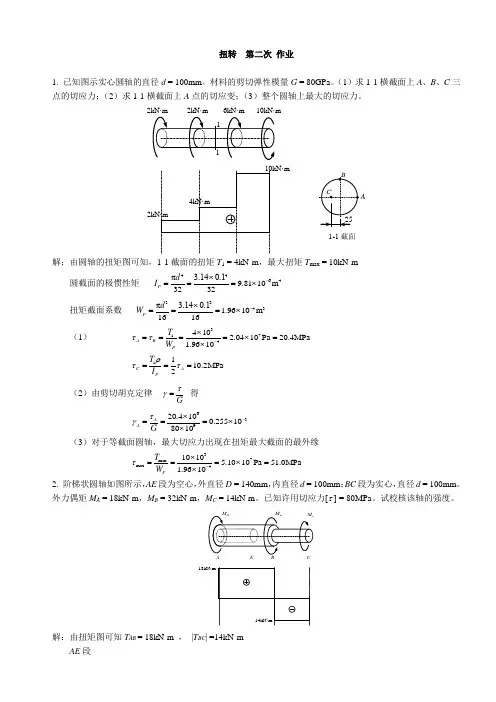
扭转 第二次 作业1. 已知图示实心圆轴的直径d = 100mm 。
材料的剪切弹性模量G = 80GPa 。
(1)求1-1横截面上A 、B 、C 三点的切应力;(2)求1-1横截面上A 点的切应变;(3)整个圆轴上最大的切应力。
2kN·m6kN·m10kN·m2kN·m1-1截面2kN·m4kN·m10kN·m解:由圆轴的扭矩图可知,1-1截面的扭矩T 1 = 4kN·m ,最大扭矩T max = 10kN·m圆截面的极惯性矩 4464π 3.140.19.8110m 3232P d I -⨯===⨯扭矩截面系数 3343π 3.140.1 1.9610m 1616P d W -⨯===⨯(1) 3714410 2.0410Pa 20.4MPa 1.9610A B P T W ττ-⨯====⨯=⨯ 1110.2MPa 2C A P T I ρττ=== (2)由剪切胡克定律 Gτγ=得63920.4100.255108010AA G τγ-⨯===⨯⨯ (3)对于等截面圆轴,最大切应力出现在扭矩最大截面的最外缘37max max41010 5.1010Pa 51.0MPa 1.9610P T W τ-⨯===⨯=⨯ 2. 阶梯状圆轴如图所示,AE 段为空心,外直径D = 140mm ,内直径d = 100mm ;BC 段为实心,直径d = 100mm 。
外力偶矩M A = 18kN·m ,M B = 32kN·m ,M C = 14kN·m 。
已知许用切应力[τ ] = 80MPa 。
试校核该轴的强度。
18kN·m14kN·m解:由扭矩图可知T AB = 18kN·m , |T BC | =14kN·mAE 段()4334431π 3.140.1410011 3.9810m 1616140P D W α-⎛⎫⨯⎛⎫=-=-=⨯ ⎪ ⎪ ⎪⎝⎭⎝⎭[]36max41181045.210Pa 45.2MPa<3.9810AB P T W ττ-⨯===⨯=⨯ BC 段33432π 3.140.1 1.9610m 1616P d W -⨯===⨯ []36max 42141071.410Pa 71.4MPa<1.9610BC P T W ττ-⨯===⨯=⨯ 故,该轴安全。


材料力学 扭转扭转的概念扭转是杆件变形的一种基本形式。
在工程实际中以扭转为主要变形的杆件也是比较多的,例如图6-1所示汽车方向盘的操纵杆,两端分别受到驾驶员作用于方向盘上的外力偶和转向器的反力偶的作用;图6-2所示为水轮机与发电机的连接主轴,两端分别受到由水作用于叶片的主动力偶和发电机的反力偶的作用;图6-3所示为机器中的传动轴,它也同样受主动力偶和反力偶的作用,使轴发生扭转变形。
图6—1 图6—2 图6—3这些实例的共同特点是:在杆件的两端作用两个大小相等、方向相反、且作用平面与杆件轴线垂直的力偶,使杆件的任意两个截面都发生绕杆件轴线的相对转动。
这种形式的变形称为扭转变形(见图6-4)。
以扭转变形为主的直杆件称为轴。
若杆件的截面为圆形的轴称为圆轴。
图6—4扭矩和扭矩图6.2.1 外力偶矩作用在轴上的外力偶矩,可以通过将外力向轴线简化得到,但是,在多数情况下,则是通过轴所传递的功率和轴的转速求得。
它们的关系式为 nP M 9550= (6-1) 其中:M ——外力偶矩(N ·m );P ——轴所传递的功率(KW );n ——轴的转速(r /min )。
外力偶的方向可根据下列原则确定:输入的力偶矩若为主动力矩则与轴的转动方向相同;输入的力偶矩若为被动力矩则与轴的转动方向相反。
6.2.2 扭矩圆轴在外力偶的作用下,其横截面上将产生连续分布内力。
根据截面法,这一分布内力应组成一作用在横截面内的合力偶,从而与作用在垂直于轴线平面内的外力偶相平衡。
由分布内力组成的合力偶的力偶矩,称为扭矩,用n M 表示。
扭矩的量纲和外力偶矩的量纲相同,均为N·m 或kN·m。
当作用在轴上的外力偶矩确定之后,应用截面法可以很方便地求得轴上的各横截面内的扭矩。
如图6-5(a )所示的杆,在其两端有一对大小相等、转向相反,其矩为M 的外力偶作用。
为求杆任一截面m-m 的扭矩,可假想地将杆沿截面m-m 切开分成两段,考察其中任一部分的平衡,例如图6-5(b )中所示的左端。

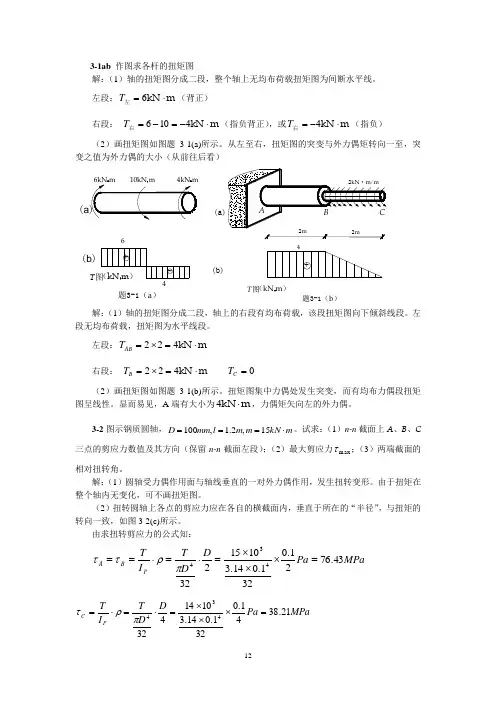
3-1ab 作图求各杆的扭矩图 解:(1)轴的扭矩图分成二段,整个轴上无均布荷载扭矩图为间断水平线。
左段:m kN ⋅=6左T (背正)右段: m kN ⋅-=-=4106右T (指负背正),或m kN ⋅-=4右T (指负) (2)画扭矩图如图题3-1(a)所示。
从左至右,扭矩图的突变与外力偶矩转向一至,突变之值为外力偶的大小(从前往后看)m10kN 4kN mT (b )(a 题3-1(a )(b)T 图(kN m )4+题3-1(b )2m2m解:(1)轴的扭矩图分成二段,轴上的右段有均布荷载,该段扭矩图向下倾斜线段。
左段无均布荷载,扭矩图为水平线段。
左段:m kN ⋅=⨯=422AB T 右段: 0422=⋅=⨯=C B T T mkN(2)画扭矩图如图题3-1(b)所示。
扭矩图集中力偶处发生突变,而有均布力偶段扭矩图呈线性。
显而易见,A 端有大小为m kN ⋅4,力偶矩矢向左的外力偶。
3-2图示钢质圆轴,m kN m m l mm D ⋅===15,2.1,100。
试求:(1)n-n 截面上A 、B 、C 三点的剪应力数值及其方向(保留n-n 截面左段);(2)最大剪应力m ax τ;(3)两端截面的相对扭转角。
解:(1)圆轴受力偶作用面与轴线垂直的一对外力偶作用,发生扭转变形。
由于扭矩在整个轴内无变化,可不画扭矩图。
(2)扭转圆轴上各点的剪应力应在各自的横截面内,垂直于所在的“半径”,与扭矩的转向一致,如图3-2(c)所示。
由求扭转剪应力的公式知:MPa Pa D D T I T P B A 43.7621.0321.014.31015232434=⨯⨯⨯=⋅=⋅==πρττ MPa Pa D D T I T P C 21.3841.0321.014.31014432434=⨯⨯⨯=⋅=⋅=πρτ(2)最大剪应力m ax τ,圆轴发生扭转时,边缘各点的剪应力最大。
MPa B A 43.76max ===τττ(3)由公式求两端截面的相对扭转角。
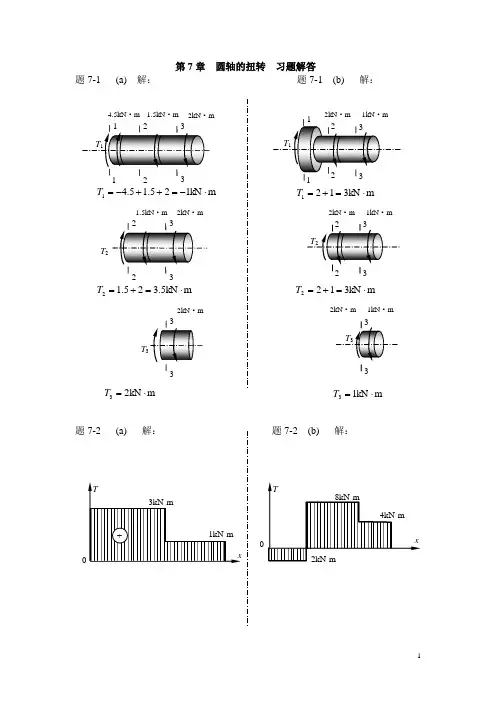
第7章 圆轴的扭转 习题解答题7-1 (a) 解: 题7-1 (b) 解:题7-2 (a) 解:4.5kN ·m 1.5kN ·m 2kN ·kN 125.15.41⋅-=++-=T 1.5kN ·m 2kN ·mT 2m kN 5.325.12⋅=+=T2kN ·mT m kN 23⋅=T 3题7-3 解:(1)计算各轮的转矩:(2)计算各段轴的扭矩:AB 段 m N 59.114e ⋅-=-=A AB M TBC 段 m 152.78N m N 37.267m N 59.114e e ⋅=⋅+⋅-=+-=B A BC M M T CD 段 m N 29.57e ⋅==D CD M T (3)绘制扭矩图题7-4 解:(1)计算各段轴的扭矩AB 段 BC 段CD 段(2)计算各截面上的最大切应力1-1截面 ()53M P a Pa 103.5mm kN 3.11616733P max 1=⨯=10⨯50π⋅⨯=π==3-AB AB AB D T W T A B τ 2-2截面 ()20.5M P a Pa 1005.2mmkN 7.11616733P max 2=⨯=10⨯75π⋅⨯=π==3-BC BC BC D T W T B C τm57.29N m N 2505.195499549m 95.49N m N 2505.295499549m 114.59N m N 250395499549e e e ⋅=⋅==⋅=⋅==⋅=⋅==n P M n P M n P M D D C CA A m267.37N m N 250795499549e ⋅=⋅==n P M B B m kN 7.0m1.7kN m 3kN m kN 3.1m kN 3.1e e e e ⋅==⋅=⋅+⋅-=+-=⋅-=-=D CD B A BC A AB M T M M T M T3-3截面 ()28.5M P a Pa 1085.2m1050m kN 7.016167333P max 3=⨯=⨯π⋅⨯=π==-CD CD CD D T W T CD τ (3)绘制扭矩图题7-5 解:(1)计算轴上扭矩m 716.18N m N 1005.795499549⋅=⋅==n P T (2)计算实心轴D 1[]45m m m 104.5m 18.71616162-331=⨯=10⨯40⨯π⨯=π≥6τT D (3)计算空心轴D 2[]46m m m 106.4m )18.71616)1(162342=⨯=0.5-(1⨯10⨯40⨯π⨯=-π≥-463ατT D题7-6 解:(1)校核轴的强度()51M P aPa 10519025.2901m mN 105.116)1(16643343P max=⨯=⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛⨯--⨯10⨯90⨯π⋅⨯⨯=-π==3-ατD T W T []M P a60MPa 51max =<=ττ (2)计算实心轴D 153m m m 105.3m 1051105.116162-63max 1=⨯=⨯⨯π⨯⨯=π≥33τT D (3)比较空心轴与实心轴的重量之比()()()()31.0mm 26.5mm 42.5452D 5.22D 2D 222222122=-=⎪⎭⎫ ⎝⎛π--π==实心轴空心轴实心轴空心轴A A W W题7-7 解:(1)计算最大起重载荷W(2)计算轴的直径由于轴上各段的扭矩绝对值相等,故只需计算一段轴的直径即可。


第三章扭转一、是非判断题1.圆杆受扭时,杆内各点处于纯剪切状态。
(×)2.杆件受扭时,横截面上的最大切应力发生在距截面形心最远处。
(×)3.薄壁圆管和空心圆管的扭转切应力公式完全一样。
(×)4.圆杆扭转变形实质上是剪切变形。
(×)5.非圆截面杆不能应用圆截面杆扭转切应力公式,是因为非圆截面杆扭转时“平截面假设”不能成立。
(√)6.材料相同的圆杆,他们的剪切强度条件和扭转强度条件中,许用应力的意义相同,数值相等。
(×)7.切应力互等定理仅适用于纯剪切情况。
(×)8.受扭杆件的扭矩,仅与杆件受到的转矩(外力偶矩)有关,而与杆件的材料及其横截面的大小、形状无关。
(√)9.受扭圆轴在横截面上和包含轴的纵向截面上均无正应力。
(√)10.受扭圆轴的最大切应力只出现在横截面上。
(×)11.受扭圆轴内最大拉应力的值和最大切应力的值相等。
(√)12.因木材沿纤维方向的抗剪能力差,故若受扭木质圆杆的轴线与木材纤维方向平行,当扭距达到某一极限值时,圆杆将沿轴线方向出现裂纹。
(×)二、选择题1.内、外径之比为α的空心圆轴,扭转时轴内的最大切应力为τ,这时横截面上内边缘的切应力为 ( B )A τ;B ατ;C 零;D (1- 4α)τ 2.实心圆轴扭转时,不发生屈服的极限扭矩为T ,若将其横截面面积增加一倍,则极限扭矩为( C )0 B 20T 0 D 40T 3.两根受扭圆轴的直径和长度均相同,但材料C 不同,在扭矩相同的情况下,它们的最大切应力τ、τ和扭转角ψ、ψ之间的关系为( B )A 1τ=τ2, φ1=φ2B 1τ=τ2, φ1≠φ2C 1τ≠τ2, φ1=φ2D 1τ≠τ2, φ1≠φ2 4.阶梯圆轴的最大切应力发生在( D ) A 扭矩最大的截面; B 直径最小的截面; C 单位长度扭转角最大的截面; D 不能确定。
5.空心圆轴的外径为D ,内径为d, α=d /D,其抗扭截面系数为 ( D ) A ()31 16p D W πα=- B ()321 16p D W πα=-C ()331 16p D W πα=- D ()341 16pD Wπα=-6.对于受扭的圆轴,关于如下结论: ①最大剪应力只出现在横截面上;②在横截面上和包含杆件的纵向截面上均无正应力;③圆轴内最大拉应力的值和最大剪应力的值相等。
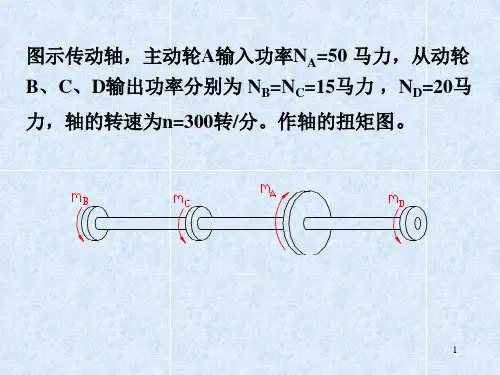
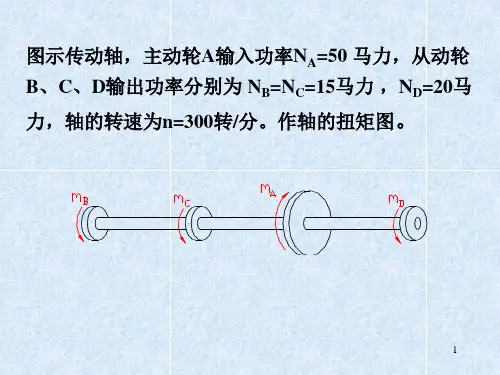
主要知识点:(1)圆轴扭转的概念、扭矩和扭矩图;(2)圆轴扭转时的应力和强度计算;(3)圆轴扭转时的变形和刚度计算。
圆轴扭转的概念、扭矩和扭矩图1. 已知圆杆横截面上的扭矩,试画出截面上与T对应的切应力分布图。
解:截面上与T对应的切应力分布图如下:2. 用截面法求下图所示各杆在1-1、2-2、3-3截面上的扭矩。
图7-2解:a)采用截面法计算扭矩(见图7-2a)。
取1-1截面左侧外力偶矩计算,可得T1 1 3kN m。
取2-2截面左侧外力偶矩计算,由平衡方程(1 2 6 kN m T2 2 0,可得T2 2 3kN m。
取3-3截面右侧外力偶矩计算,可得T3 3 1kN m。
b)采用截面法计算扭矩(见图7-2b )。
取1-1截面左侧外力偶矩计算,可得T1 15kN m。
取2-2截面左侧外力偶矩计算,由平衡方程(5 5 kN m T2 2 0,可得T2 2 10kN m。
取3-3截面右侧外力偶矩计算,由平衡方程(3 3 kN m T3 3 0,可得T3 3 6kN m。
3•作下图各杆的扭矩图。
解:a)采用截面法计算扭矩(见图7-3a )。
取1-1截面左侧外力偶矩计算,可得T1 1 4kN m。
取2-2截面右侧外力偶矩计算,可得T2 2 2kN m。
作出扭矩图。
a)b)图7-3b)由力矩平衡方程可得M A 2M e(负号表示与图中假设方向相反)。
采用截面法计算扭矩(见图7-3b )。
取1-1截面左侧外力偶矩计算,可得T1 1 2M e。
取2-2截面右侧外力偶矩计算,可得T2 2M e。
作出扭矩图。
圆轴扭转时的应力和强度计算4. 实心圆轴和空心轴通过牙嵌离合器而连接,如图所示。
已知轴的转速n=100r/min,传递的功率p=,材料的许用应力[]=40MP,试通过计算确定(1)采用实心轴时,直径d1和的大小;(2)采用内外径比值为1/2的空心轴时,外径D2的大小。
解:计算外力偶矩,作用在轴上的外力偶矩:T 9550P 9550 恥N m 716N mn 1005. 如图所示为皮带传动轴,轴的直径有四个皮带轮。
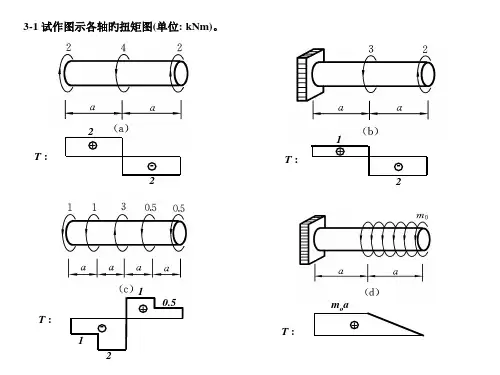
第3章作业参考解答3-1试作附图中各圆杆的扭矩图。
习题3-1附图解答各杆的轴力图分别见解答附图(a)、(b)、(c)、(d)。
2TT3T (a)M x4T10100(c)M x /N ·m51(b)M x /kN ·m32.521.5(d)M x /kN ·m3-2一传动轴以每分钟200转的角速度转动,轴上装有4个轮子,如附图,主动轮2输入功率60kW ,从动轮1,3,4依次输出功率15kW ,15kW 和30kW 。
(1)作轴的扭矩图。
T 4T 3T 2T 1(2)将2,3轮的位置对调,扭矩图有何变化?解答(1)各轮上作用的力偶矩为15´103´60T 1==0.716kN ×m 2p ´20060´103´60T 2==2.865kN ×m ,2p ´20015´103´60T 3==0.716kN ×m 2p ´2001.432习题3-2附图2.1491.4320.716(a)M x /kN ·m30´103´60T 4==1.432kN ×m 2p ´2000.716扭矩图见附图(a),最大扭矩为Mx max=2.149kN ×m 。
1.432(b)M x /kN ·m(2)2,3轮的位置对调后扭矩图见附图(b),最大扭矩为Mx max=1.432kN ×m 。
3-3一直径d =60mm 的圆杆,其两端受T =2kN·m 的外力偶矩作用而发生扭转,如附图示。
设轴的切变模量G =80GPa 。
试求横截面上1,2,3点处的切应力和最大切应变,并在此三点处画出切应力的方向。
解答1,2,3点处的切应力分别为t 2=0.0T 2000t 3===47.2MPa 3W p 3.14´0.06/16t 1=2t 3/3=31.4MPa切应力方向见附图(1)。
扭转的强度条件-例题分析例题1—1 一电机传动钢轴,直径d = 40mm ,轴传递的功率30kW ,转速n = 1400r/min 。
轴的许用切应力[]τ= 40MPa,试校核此轴的强度。
解:(1)计算扭力偶矩和扭矩。
扭力偶距为x m = 9550n P = 9550140030⨯= 204×103 (N ·mm ) 由截面法求得轴横截面上的扭矩为: 320410(N mm)x T m ==⨯⋅(2) 强度校核。
轴的抗扭截面系数为 334320 1.25510(mm )22R W ρππ⨯===⨯3maxmax 42041016.3(MPa)1.25510T W ρτ⨯==⨯ 因为 max []40(MPa)ττ<=轴满足扭转强度条件。
例题1-2 如图所示为汽车传动轴简图,轴选用无缝钢管,其外半径45mm R =,内半径42.5mm r =.许用剪应力[]τ=60MPa ,根据强度条件,求轴能承受的最大扭矩。
例题1—2图解:按强度条件确定最大扭矩。
42.50.94445r R α=== 3344345(1)(10.944)29400(mm )22R W ρππα⨯=-=-=由强度条件得3max []6029400176410(N mm)1764(N m)T W ρτ≤=⨯=⨯⋅=⋅轴能承受的最大扭矩为1764N m ⋅。
例题1—3 某传动轴,轴内的最大扭矩max 1.5kN m T =⋅,若许用切应力[]τ=50MPa,试按下列两种方案确定轴的横截面尺寸,并比较其重量.①实心圆截面轴;②空心圆截面轴,其内、外半径的比值9.022=R r 。
解:(1)确定实心圆轴的半径。
根据强度条公式可得 []max T W ρτ≥ 将实心圆轴的抗扭截面系数32R W ρπ=代入上式得6max 33122 1.51026.73(mm)[]50T R πτπ⨯⨯=⨯ 取 )(271mm R =(2)确定空心圆轴的内、外半径.将空心圆轴的抗扭截面系数()3412R W ρπα=-代入强度条件式可得6max 3324422 1.51038.15(mm)[].(1)50(10.9)T R πταπ⨯⨯-⨯⨯- 其内半径相应为220.90.938.1534.34(mm)r R ==⨯=取 239(mm)R = 234(mm)r =(3)重量比较。
扭转典型习题解析1 一内径d =100mm 的空心圆轴如图示,已知圆轴受扭矩m kN 5⋅=T ,许用切应力][τ=80MPa ,试确定空心圆轴的壁厚。
解题分析:因为不知道壁厚,所以不能确定是不是薄壁圆管。
分别按薄壁圆管和空心圆轴设计。
解: 1、按薄壁圆管设计薄壁圆管扭转时,假设切应力沿壁厚均匀分布,设壁厚为δ,平均半径为2/0)(δ+=d R ,则扭转切应力为 δτ20π2R T=强度条件为][ττ≤,于是得][π22τδδTd =+)( ][π22223τδδδTd d =++ ()Pa1080πm N 1052m 10100m 1010026323233××⋅××=×+××+−−δδδ解得 mm 70.3m 1070.33=×=−δ 2、按空心圆轴设计强度条件为 ][pmax ττ≤=W T将δ216π44p +=−=d D d D DW );(代入得][π16][π][π164444=−−≤−τττd TD D d D DT,)(0Pa)108(m 1.0πm N 10516Pa 1080π64346=××−×⋅××−×××)(D D解得mm 107.7m 10107.73=×=−Dmm 85.32mm100mm 7.1072=−=−=d D δ 比较可知,两种设计的结果非常接近。
讨论: 当10/0R ≤δ时,即认为是薄壁圆管,可以直接使用薄壁管扭转公式。
2 图示受扭圆杆,沿平面ABCD 截取下半部分为研究对象,如图b 所示。
试问截面ABCD 上的切向内力所形成的力偶矩将由哪个力偶矩来平衡?解题分析:由切应力互等定理可知截面ABCD 上的切向内力分布及其大小。
该截面上切向内力形成一个垂直向上的力偶矩。
在图b 中,左右两个横截面上的水平切向内力分量形成垂直于截面ABCD 的竖直向下的力偶矩,正好与截面ABCD 上切向内力的合力偶矩平衡。
解:1、计算长为 l 的纵截面ABCD 上切向内力的合力偶矩如图c所示,在纵截面上取一微面积ρd d ⋅=l A ,其上切向内力的合力即微剪力ρρρτd d d pρS ⋅⋅=⋅⋅=l I Tl F 微剪力对 z 轴的微力矩为ρρρτρρd d d d 2pρS ⋅⋅=⋅⋅==l I T l F M z 积分得到纵截面上切向内力对 z 轴的合力偶矩为题2图(c)p32p 32d 2d I TlR l I T M M R z z =⋅⋅==∫∫ρρ,方向竖直向上。
2、计算两端横截面切向内力的水平分量形成的力偶矩 如图d所示,微面积θρρd d d =A 上切向内力的水平分量为θρθρθθρρτd d sin sin d d d 2pρ⋅=⋅⋅=I T F 右端横截面上剪力的水平分量为3p2p 2π0S 32d d sin 2R I T I T F R ==∫∫θρθρ 左右两个横截面上水平剪力形成绕 z 轴的力偶矩为3pS 32lR I Tl F =⋅,竖直向下。
所以,截面ABCD 上的切向内力所形成的力偶矩将由左右两个横截面上水平剪力形成的力偶矩平衡。
3 空心钢轴的外径 D = 100 mm ,内径 d = 50 mm 。
已知间距 l = 2.7 m 之间两截面的相对扭转角ϕ=1.8°,材料的切变模量G = 80 GPa 。
试计算:(1) 轴内最大切应力;(2) 当轴以 n = 80r/min 的速度旋转时,轴传递的功率(kW)。
解题分析:由已知条件ϕ求出扭矩T ,由 T 计算xa m τ和功率P 。
解:1、根据相对扭转角列出扭矩的表达式π180p °×=GI Tl ϕ,即lGI T °=180πp ϕ 2、计算最大切应力MPa6.46Pa 106.46180m7.22m1.0Pa π10808.11802π1802π269p p p max=×=°×××××°=°×=°××=⋅=l D G l I D GI I DT ϕϕτ 3、计算轴传递的功率由{}{}r/min kW 412442980954932m 1050100πm 7.2180Pa 10808.1P T =×−××°××°=−)(得kW 7.71=P4 若用一内外径比值为0.6的空心轴来代替直径为 d = 400 mm 的实心轴,在两轴的许用切应力相等的条件下,试确定空心轴的外径,并比较实心轴和空心轴的重量。
解题分析:用空心轴代替实心轴,须保证二者强度相同。
根据强度条件可求出D 值,再用面积比得出重量比。
解:1、根据两轴切应力相等的条件,确定空心轴外径][P max实P max τ==空W T W T )1(16π16π433α−=D d mm 420)6.01(1mm400)1(1)1(4343433=−=−=−=ααdd D2、比较实心轴和空心轴的重量两轴重量比应等于其横截面面积空A 和实A 之比:%71%100mm 4006.01mm 4204π)1(4π22222222=×−=−=)(实空d D A A α 即在强度相同条件下,空心轴可以节约近30%的材料。
讨论:在实际工程中常用空心圆轴代替实心圆轴,在保障安全运行的前提下,可以节约材料。
5 已知钻探机杆的外径D = 60 mm ,内径d = 50 mm ,功率P = 7.46 kW ,转速n =180 r/min ,钻杆入土深度l = 40 m ,G = 80 GPa ,[τ]= 40 MPa 。
设土壤对钻杆的阻力是沿长度均匀分布的,试求:(1) 单位长度上土壤对钻杆的阻力矩M ;(2) 作钻杆的扭矩图,并进行强度校核; (3) 求A 、B 两截面相对扭转角。
解题分析:根据题意,为圆轴扭转问题。
土壤对钻杆的阻力形成扭力矩作用在钻杆上,并沿钻杆长度方向均匀分布。
解:1、求阻力矩集度M设钻机输出的功率完全用于克服土壤阻力,则有m N 390min/r 180kW46.79549}{}{9549min r kW ⋅===n P T单位长度阻力矩m/m N 75.9m 40mN 390⋅=⋅==lT M2、作扭矩图,进行强度校核钻杆的扭矩图如图 c 所示。
最大扭矩出现在A 截面,所以A 截面为危险截面。
其上最大切应力为[]ττ<=×−××⋅=×=−−MPa 7.17m 10)5060(32πm1030m N 390412443p max maxI R T满足强度要求。
3、计算A 、B 两截面相对扭转角ϕAB2·d ·d · p 0p0p l GI T x GI l xT GI x M ll AB===∫∫ϕ°==××−×××⋅×=−8.48rad 0.1482m 10]5060[πPa 1080m04m N 39032 412449)()( 6 两个等长度的钢管松套在一起。
外管的尺寸为D 1=100 mm ,d 1=90 mm ;内管的尺寸D 2 = 90 mm ,d 2 = 80 mm 。
当内管受扭矩T = 2 kN·m 作用时,将两管的两端焊接起来。
然后去掉内管上的扭矩,问此时组合管内将产生怎样的应力?试画出组合管横截面上的切应力分布图。
解题分析:内、外管两端焊接后,内、外管在端截面处一起变形。
去掉内管扭矩后,内管产生恢复性扭转变形,并带动外管也产生扭转变形。
同时外管限制内管完全恢复到其受扭前位置。
两管在中间位置取得平衡。
此题属于扭转静不定问题。
解:设预加扭矩T 在内管引起的扭转角为ϕ;在焊接后和去掉内管扭矩后,设外管所受扭矩为T 1,相应扭转角为ϕ1,内管所受扭矩为T 2,相应扭转角为ϕ2。
1、列静力平衡方程21T T =(a )2、列变形协调方程21ϕϕϕ+=(b )代入物理关系得p22p11p2GI l T GI l T GI Tl+= (c) 3、计算各管扭矩将(a)、(c)联立求解,得 )()()(414142424141p1p2p11d D d D d D T I I TI T −+−−=+=241244412444124431m N 1166m 1090100m 108090m 1090100m N 102T T =⋅=×−+×−×−⋅×=−−−)()()(4、计算外管和内管的切应力MPa 3.17Pa 103.17m 1090100π32m 1050m N 116626412443p111max 1=×=×−×××⋅=×=−−)(I D T τ MPa 8.21Pa 108.21m 10)8090(π32m 1045m N 116626412-443-p2222max =×=×−×××⋅=×=I D T τ组合管的切应力分布图如图b 所示。
7 一圆形截面杆和矩形截面杆受到相同扭矩T = 400 N ·m 作用,圆杆直径d = 40 mm ,矩形截面为60 mm ×20 mm ,试比较这两种杆的最大切应力和截面面积。
解题分析:圆形截面杆受扭时最大切应力发生在截面边缘各点处,矩形截面杆受扭时最大切应力发生在截面长边中点处。
计算时需要先查表得到有关系数。
解:1、分别计算两种截面杆最大切应力圆杆MPa 9.31Pa 109.31m)1040(πm N 40016π166333p max =×=××⋅×===−d T W T τ 矩形杆,先计算比值326==b h ,查表267.0=α MPa 4.62Pa 104.62m)1060(m 1020267.0mN 40063232max =×=××××⋅==−−)(hb Tατ2、分别计算两杆截面面积圆杆()mm 1260m 1012604m 1040π26-22-3=×=××=圆A矩形杆1200mm m 101200m 1020602626=×=××=−−矩A讨论:矩形截面面积与圆形面积相近,但是最大切应力却增大了近一倍,且bh之值越大,切应力也越大,因此工程中应尽量避免使用矩形截面杆作扭转杆件。