材料力学:ch12 弯曲问题进一步研究
- 格式:pdf
- 大小:301.50 KB
- 文档页数:15

材料力学实验报告材料力学实验报告实验名称:弯曲实验实验目的:研究材料的弯曲性质,探究其弯曲应力和弯曲应变之间的关系。
实验原理:当材料受到外力作用时,会发生形变,弯曲是其中一种形变。
在实验中,我们用到了一根长而细的金属棒,将其固定在中间部分,然后在两端施加对称的力,使其发生弯曲。
实验装置:弯曲金属棒、测力计、直尺、螺钉刻度尺。
实验步骤:1. 将金属棒放置在实验台上,用螺钉将其固定在中间部分。
2. 在金属棒的两端分别固定测力计,用直尺测量两个测力计之间的距离,并记录下来。
3. 分别给两个测力计施加相同的力,并记录下测力计示数。
4. 分别调整测力计,给金属棒施加不同大小的力,并记录下测力计示数及对应的距离。
5. 分别拧松两端的螺钉,测量金属棒在不同载荷下的变形情况。
6. 根据实验数据计算出金属棒的弯曲应力和弯曲应变,并绘制出应力 - 应变曲线。
实验结果与分析:根据实验数据计算出金属棒在不同载荷下的弯曲应力和弯曲应变,并绘制了应力 - 应变曲线。
通过对曲线的分析,我们可以得出以下结论:1. 弯曲应力与施加的力成正比,即弯曲应力随载荷的增加而增加。
2. 弯曲应力与材料的几何形状有关,即相同的载荷下,细长的材料受到的弯曲应力更大。
3. 弯曲应变与弯曲应力成正比,即弯曲应变随弯曲应力的增加而增加。
4. 材料的弯曲模量是材料力学性质的一种度量,表示单位应力下的弯曲应变。
在本实验中,我们可以通过斜率来计算出弯曲模量。
结论:通过本次实验,我们研究了材料的弯曲性质,并探究了弯曲应力和弯曲应变之间的关系。
实验结果表明,材料的弯曲应力和弯曲应变是成正比的,且与材料的几何形状有关。
弯曲模量是材料力学性质的一种重要参数,可以通过斜率来计算。
这些结果对于工程设计和材料选择具有一定的指导意义。
参考文献:[1] 张三,杨明. 材料力学实验讲义. 北京:科学出版社,2008.[2] 李四,王五. 材料力学实验指南. 上海:上海大学出版社,2010.。


一实验目的
1更好的了解弯曲时材料所受载荷的变化
2帮助我们了解材料弯曲实验的原理
3提高我们解决问题的能力
二实验仪器
自制弯曲试验仪
三实验原理
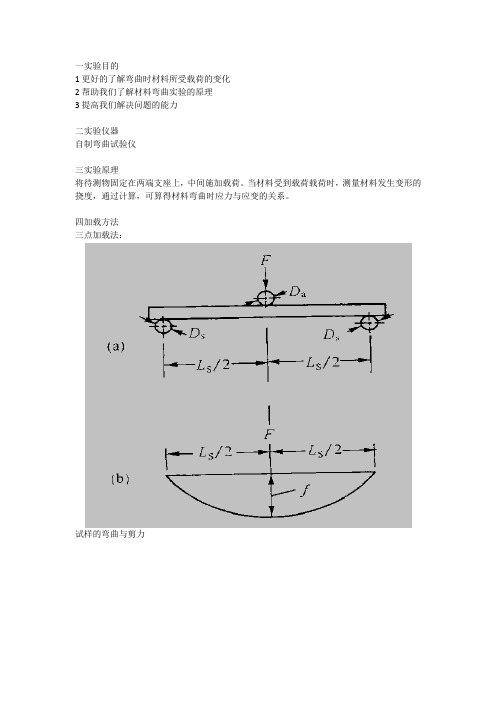
将待测物固定在两端支座上,中间施加载荷。
当材料受到载荷载荷时,测量材料发生变形的挠度,通过计算,可算得材料弯曲时应力与应变的关系。
四加载方法
三点加载法:
试样的弯曲与剪力
4max S FL M = 2
F Q =
四点加载法:
试样的弯矩与剪力
2
max Fl M = 2F Q =
正应力计算
根据材料力学的变形假设,变形前后试样的各横截面都是平面,且与试样轴线垂直。
由此可推导出弯曲试样横截面上任一点正应力按下式计算:
I My =
σ 式中:
M ——弯矩,N·mm
y ——横截面上任一点到中性轴的距离,mm
I —— 试样横截面对中性轴的惯性矩 对圆截面试样644
d I π= 对矩形截面试样123
bh I =
θ≈30°。


材料弯曲实验报告引言弯曲实验是材料力学实验中常用的一种实验方法,通过施加力使材料发生弯曲变形,从而研究材料的力学性能。
本实验旨在探究材料的弯曲行为,并分析其与材料的力学性能之间的关系。
实验装置与材料本次实验使用的主要装置为一台弯曲试验机,其包括一个加载系统和一个记录和读取弯曲力的力传感器。
我们选取了常见的金属材料——钢板作为实验材料。
实验步骤1.准备工作:将实验装置调整至合适的工作状态,确保其能够稳定运行,并保证实验材料的质量和尺寸符合要求。
2.安装实验材料:将待测试的钢板固定在弯曲试验机上,并确保其固定牢固。
3.设置实验参数:根据实验要求,设定加载系统的初始位置、载荷速度以及加载方式等实验参数。
4.开始实验:启动弯曲试验机,加载系统会开始施加力对实验材料进行弯曲。
同时,力传感器将持续记录所施加的力大小。
5.读取数据:实验过程中,及时读取并记录所施加的力大小和相应的位移值。
可以利用计算机系统进行数据记录和处理。
6.结束实验:当实验材料发生破坏或达到预设的弯曲程度时,停止加载系统的运动,并记录最终弯曲力和位移数值。
7.数据分析:根据实验结果,通过绘制弯曲力-位移曲线和弯曲应力-应变曲线,分析材料的弯曲性能。
实验数据与结果在本次实验中,我们记录了实验材料在不同载荷下的弯曲力-位移数据,并绘制了相应的力-位移曲线。
通过对实验数据的分析,我们得到了以下结论: 1. 随着加载力的增加,材料的位移也随之增加,但增速逐渐减缓,呈现出一种非线性关系。
2. 在一定范围内,弯曲力和位移呈正相关,即加载力越大,位移越大。
3. 当材料弯曲到一定程度时,会出现材料发生破坏的情况。
结论通过本次实验,我们深入了解了材料的弯曲行为以及材料力学性能的相关因素。
我们发现,加载力对材料的位移和破坏起着重要的影响。
弯曲实验是研究材料弯曲性能的重要手段,对于材料的设计和应用具有重要意义。
参考文献1.陈永平, 杨丽敏, 刘华, 徐永健. 材料力学实验与材料力学性能评定实验教程[M]. 清华大学出版社, 2011.2.张善民, 严学飞, 袁雷. 材料刚度、强度与韧性综合化分析方法[J]. 材料导报, 2017, 31(15):132-137.3.张政权, 邢吉祥, 吉泽厚. 材料筛选软件[J]. 中国稀土学报, 2018,36(6):594-600.致谢在本次实验中,感谢实验员对实验装置和材料的准备工作和技术支持,以及指导老师对实验过程和数据分析结果的指导和帮助。
第十二章 弯曲问题进一步研究12-1 在梁的图示横截面上,弯矩M =10 kN·m 。
已知惯性矩I y=I z=4.7×106mm 4,惯性积Iyz =2.78×106mm 4,试计算最大弯曲正应力。
问题3-2图解:1. 确定危险点位置截面的主形心轴u 与v 如图b 所示,其方位角为45=α根据惯性矩转轴公式,得截面的主形心惯性矩为46464646m 1053.7m 1097.109sin )m 1078.2(m 1075.4sin2 −−−−××=××== αyz y v u I I I I 将弯矩M 沿主形心轴u 与v 分解,得相应分量分别为m N 1059.215sin m)N 1010(33⋅×=⋅×= u Mm N 1066.915m)cos N 1010(33⋅×=⋅×= v M 于是得中性轴的方位角为8144)m 107.53)(m N 1059.2()m 10m)(1.97N 1066.9(arctan arctan 463463′=×⋅××⋅×==−− v u u v I M I M ϕ 其方位如图b 所示。
可见,在截面的角点a 与b 处,分别作用有最大弯曲拉应力与最大弯曲压应力。
2. 最大弯曲应力计算在坐标系C-yz 内,角点a 的坐标为,m 084.0−=a y m 020.0−=a z 在坐标系C-uv 内,该点的坐标则为 m 0735.0sin cos −=+=ααa a a z y um 0453.0sin cos =−=ααa a a y z v于是得角点a 处的弯曲正应力为MPa 156m 1053.7)m 0753.0)(m N 1066.9(m 1097.1)m 0453.0)(m N 1059.2(463463=×−⋅×−×⋅×=−=−−v a v u a u a I u M I v M σ角点b 位于坐标轴v ,其纵坐标为m 0509.0−=b v 因此,该点处的弯曲正应力为MPa 9.66m 1097.1)m 0509.0)(m N 1059.2(3−=×−⋅×==−u b u b I v M σ 可见,最大弯曲正应力为MPa 156max ==a σσ12-4 图示截面薄壁梁,剪力FS y = 5 kN 。
第十二章 弯曲问题进一步研究12-1 在梁的图示横截面上,弯矩M =10 kN·m 。
已知惯性矩I y=I z=4.7×106mm 4,惯性积Iyz =2.78×106mm 4,试计算最大弯曲正应力。
问题3-2图解:1. 确定危险点位置截面的主形心轴u 与v 如图b 所示,其方位角为45=α根据惯性矩转轴公式,得截面的主形心惯性矩为46464646m 1053.7m 1097.109sin )m 1078.2(m 1075.4sin2 −−−−××=××== αyz y v u I I I I 将弯矩M 沿主形心轴u 与v 分解,得相应分量分别为m N 1059.215sin m)N 1010(33⋅×=⋅×= u Mm N 1066.915m)cos N 1010(33⋅×=⋅×= v M 于是得中性轴的方位角为8144)m 107.53)(m N 1059.2()m 10m)(1.97N 1066.9(arctan arctan 463463′=×⋅××⋅×==−− v u u v I M I M ϕ 其方位如图b 所示。
可见,在截面的角点a 与b 处,分别作用有最大弯曲拉应力与最大弯曲压应力。
2. 最大弯曲应力计算在坐标系C-yz 内,角点a 的坐标为,m 084.0−=a y m 020.0−=a z 在坐标系C-uv 内,该点的坐标则为 m 0735.0sin cos −=+=ααa a a z y um 0453.0sin cos =−=ααa a a y z v于是得角点a 处的弯曲正应力为MPa 156m 1053.7)m 0753.0)(m N 1066.9(m 1097.1)m 0453.0)(m N 1059.2(463463=×−⋅×−×⋅×=−=−−v a v u a u a I u M I v M σ角点b 位于坐标轴v ,其纵坐标为m 0509.0−=b v 因此,该点处的弯曲正应力为MPa 9.66m 1097.1)m 0509.0)(m N 1059.2(3−=×−⋅×==−u b u b I v M σ 可见,最大弯曲正应力为MPa 156max ==a σσ12-4 图示截面薄壁梁,剪力FS y = 5 kN 。
试画弯曲切应力分布图,并计算最大弯曲切应力。
题12-4图解:设形心C 示如图12-4(1),则图12-4m 025.0m 2010.0100.0050.0010.0100.0=××××=C y464223m 1008.2m )025.0100.0010.0025.0100.0010.012100.0010.0(−×=××+××+×=z I()()1411105.2025.0010.0ηηη−×=×=Z S()())21025.0(010.0025.0100.0010.0222ηηη−+××=Z S223245105105.2105.2ηη−−−×−×+×=()MPa 00.3Pa 1000.3m010.01008.2N 1025.11056265311max ,S max ,1=×=×××××==−−δητz z y I S F ()MPa 75.6Pa 1075.6m010.01008.2N 1081.21056265322max ,S max ,2=×=×××××==−−δητz z y I S F 弯曲切应力分布图示如图12-4(2),MPa 75.6max =τ12-5 一薄壁梁,其横截面如图所示,剪力FS y = 40 kN ,壁厚δ=10 mm 。
试:(1)计算A ,B 与D 三点处的弯曲切应力; (2)确定截面的剪心位置。
题12-5图解:(1)算弯曲切应力 坐标示如图12-5。
图12-5由图可知,454323m 10335.3 m 12010.0100.02100.0010.0100.0212200.0010.02[−×=××+×××+××=z I 35322,m 1025.1m 050.02010.02)(−×=×==A A z y S δω 3432,m 10875.1 m )075.0050.0010.0100.0100.0010.0100.02010.0()(−×=××+××+×=ωB z S 据公式()()δωητz z I S F S =得MPa 499.1Pa 10499.1m 010.010335.3N 1025.1104062553=×=×××××=−−A τ MPa 5.22Pa 1025.2m010.010335.3N 10875.11040743=×=×××××=−−B τ MPa 5.22==B D ττ (因为上下对称)(2)确定截面的剪心位置因为上下对称,所以剪心必在z 轴上,问题归结为求。
z e 据合力矩定理,取G 点为矩心(见图12-5),有()200.02100.021S ×+××=⋅F F e F z y其中,zy zy I F I F q F S 63S 100.0 0111106667.13100.0005.0d −×=××==η()zy zy I F I F q F S 533S 100.0 0222100000.1100.0005.0100.0005.0d −×=×+×==⎰η于是,[][])( mm 70.0m 070.0 m 100000.1200.0106667.1200.010335.31m 200.02100.0156521S 腹板形心左侧==××+×××=+×⋅=−−−F F F e yz 12-6 试指出图示截面的剪心位置。
题12-6图解:(a )双对称截面,剪心与形心重合;(b )角钢形截面,剪心在二边条中心线相交处;(c )T 形截面,剪心在翼缘中心线与腹板中心线相交处。
12-9 试确定图示各截面的剪心位置。
题12-9图(a)解:由图12-9a(1)可知,ϕδθδθϕϕsin d cos )(2000 0R R R S z =⋅=⎰2π3R I z δ=因此,S S πsin 2)()(R F I S F q y zz y ϕϕϕ==图12-9(a)如图12-9a(2)所示,以圆心O 为矩形,根据合力矩定理可知,π4d πsin 2d )(0S ππ0S 00S R F R F R q R e F y y z y ⎰⎰==⋅=ϕϕϕϕ由此得,π40R e z =(b )解:设剪力作用于剪心E (见图12-9b ),有y F S y y y F F F S 2S 1S =+及()y y F h h h F S 3231322S +=δδ其中,和分别为左、右腹板分担的剪力。
1S y F 2S yF图12-9(b)对左腹板形心C 1取矩,有b F z F y e y 2S S =由此得b h h h b F F z y y e 323132S 2S +==(在左翼缘形心右侧)12-10 图示用钢板加固的木梁,承受载荷F= 10 kN 作用,钢与木的弹性模量分别为E s=200 GPa 与E w= 10 GPa 。
试求钢板与木梁横截面上的最大弯曲正应力以及截面C的挠度。
题12-10图解:以钢为基本材料,模量比为201s w ==E E n 等效截面示如图12-10,其形心坐标为m 1525.0m 010.0100.0200.0005.00.2050.0100.1000.1000.2000.005[=×+×××+××=C y该截面的惯性矩为()()4642323m 1085.8m ]1525.0205.0010.0100.012010.0100.0 100.01525.0200.0005.012200.0005.0[−×=−××+×+−××+×=z I由此得()()MPa 3.43Pa 1033.4m1085.83N 1525.0210.0110102210.07263max t max ,s =×=××−××××=−=−zC I y M σ MPa 74.5Pa 1074.5m1085.8320N 1525.011010216263max cmax,w =×=××××××××==−zCI y nM σ图12-10最后,根据公式)(6222b l x lEIFbx w +−=求挠度。
C w 这里,. , m,3 m,1 m,2s z I I E E l b a x ======得36942223222s m N 1085.81020036m N )132(211010)(6⋅×××××⋅+−××××=+−=−b l a I lE Fba w zC()↓−=×−=− mm 51.2 m 1051.2312-11 图示截面复合梁,在其纵向对称面内,承受正弯矩M = 50 kN·m 作用。
已知钢、铝与铜的弹性模量分别为E st =210 GPa ,E al =70 GPa 与E co = 110GPa ,试求梁内各组成部分的最大弯曲正应力。
题12-11图(a )解:以钢为基本材料,模量比为31st al ==E E n 等效截面示如图12-11a ,其形心坐标为()m 1786.0m200.0100.03100.0100.0m 200.0200.0100.03050.0100.0100.023=×+×××+××=C y 该截面的惯性矩为()()44423223m 10337.1m ]1786.0200.0200.0100.012200.0100.0 050.01786.0100.031312100.0100.0[−×=−××+×+−××+××=z I由此得MPa 3.22Pa 1023.2m 10337.13N 1786.010507243cmax,al =×=××××==−zC I nMy σ () MPa 4.45Pa 1054.4m 10337.1N 1214.01050300.07243tmax,st =×=×××=−=−zC I yM σ图12-11(b )解:以钢为基本材料,模量比分别为31st al 1==E E n 2111st co 2==E E n 等效截面示如图12-11b ,其形心坐标为m1603.0 m )2111100.0100.0100.0100.03100.0100.0(m )2111250.0100.0100.0150.0100.0100.03050.0100.0100.0(23=××+×+××××+××+××=C y 该截面的惯性矩为()()()45422323223m 1092.9 =m 211603.0250.0100.0112112100.0100.011150.01603.0100.0100.0 12100.0100.03050.01603.0100.0312100.0100.0[−×−××+×××+−××+×+−×+××=z I 由此得MPa 9.26Pa 1069.2m 1092.93N 1603.0105072531cmax,al =×=××××==−zC I My n σ()MPa 4.30Pa 1004.3m 1092.9N 0603.01050100.07253cmax,st =×=×××=−=−zC I y M σ()MPa 9.36Pa 1069.3m 1092.921N 1397.010*******.072532tmax,co =×=×××××=−=−zC I y M n σ (c )解:根据及al st M M M +=alal alst st st I E M I E M = 得由此得M M 4248.0st =M M 5752.0al =MPa 2.108Pa 10082.1 P )100.0150.0π(075.06410505752.08443max,al =×=−××××=a σ MPa 216Pa 1016.2 Pa 100.0π3210504248.0833maxst,=×=××××=σ 12-12 图示简支梁,承受均布载荷作用,该梁由木材与加强钢板组成。