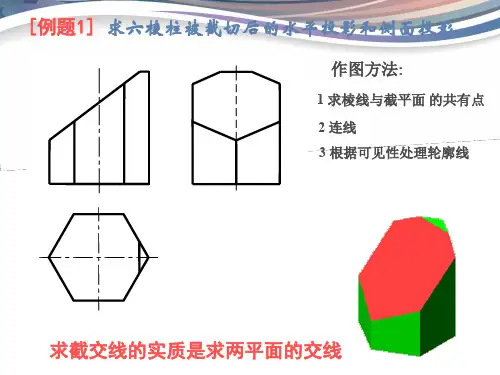
截交线相贯线习题及答案
- 格式:ppt
- 大小:28.20 MB
- 文档页数:110

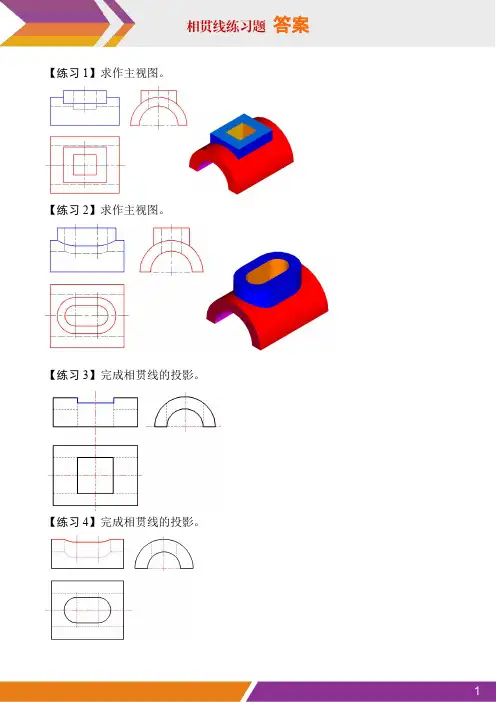
【练习1】求作主视图。
【练习2】求作主视图。
【练习3】完成相贯线的投影。
【练习4】完成相贯线的投影。
【练习5】完成立体的正面投影。
【练习6】求作左视图。
【练习7】求作俯视图。
【练习8】求立体的相贯线,完成正面投影。
【练习10】求作俯视图。
【练习11】求作俯视图。
(1)
(2)
【练习13】求作主视图。
【练习14】完成相贯线的投影。
【练习15】完成相贯线的投影。
【练习16】完成相贯线的投影。
【练习17】求作左视图。
【练习18】求作左视图。
【练习19】求作左视图。
【练习20】求作俯视图。
【练习21】求作主视图。
【练习22】求作左视图。
(1)
(2)
【练习23】求作左视图。
【练习24】求作左视图。
【练习25】求作左视图。
【练习26】完成立体的投影。
【*练习27】完成立体的投影。
【*练习28】完成立体的投影。
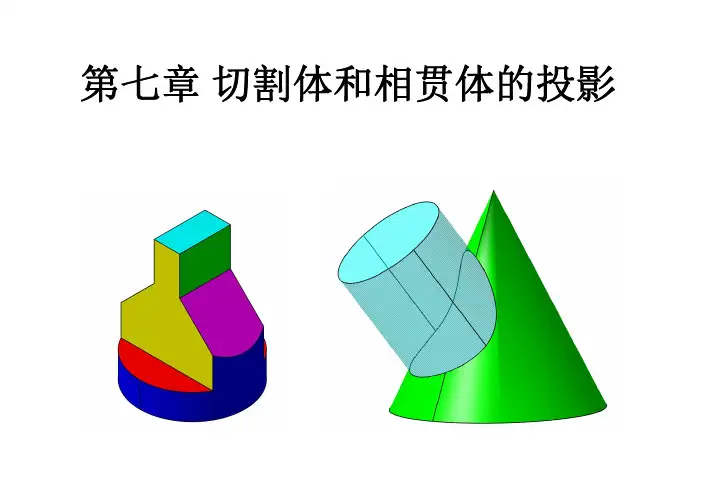


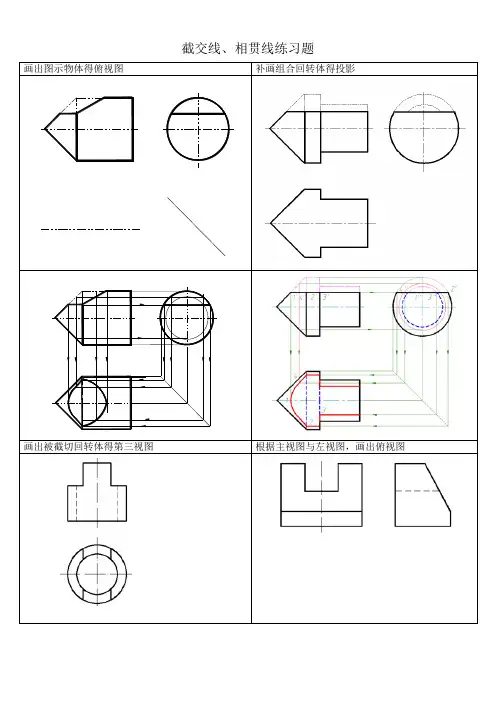
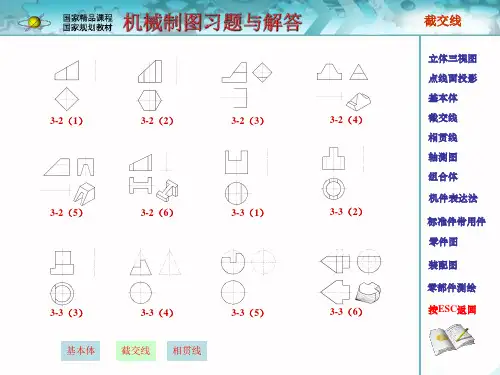
截交线、相贯线练习题
画出图示物体得俯视图补画组合回转体得投影
画出被截切回转体得第三视图根据主视图与左视图,画出俯视图
画出图示物体得主视图求作立体得H面投影
补画立体得水平投影分析曲面立体得截交线,补全曲面立体得三面投影
补画立体得水平投影补画半球切割后得投影
补画圆锥与半球相贯得V面与H面投影补画圆柱与半球相贯得V面与H面投影
画出两圆柱面得相贯线。
(不能用圆弧来替代,要求
作以下立体得相贯线
保留辅助线)
画出圆柱面得内外相贯线根据主视图与左视图,画出俯视图中得相贯线
画出图示物体得俯视图补画下面物体得投影
完成圆柱与圆锥相贯后得正面投影与水平投影。



项目4组合体的投影4.1看图填空并补画图中所缺的图线(1)请将左图中满足条件的图号填在相应的横线上:左图中属于叠加型组合体的有2、3、1,属于切割型组合体的有5、6,属于综合型组合体的有L表面连接关系为相切的有2、3、6,表面连接关系为相交的有2、3、5,表面连接关系为共面有1、L表面不共面的有1、5。
(2)仔细分析图中组合体的组合型式并补面图中所缺的图线。
A.平行B.垂直C.倾斜D.相交4.当截平面与圆柱体平行时,截交线为(A )oA.矩形B.椭圆C.圆D.正方形5.当截平面与圆柱体(B )时,截交线为圆。
A.平行B.垂直C.倾斜D.相交。
6.当截平面与圆球体相交时,截交线为(C )oA.矩形B.椭圆C.圆D.正方形7.当截平面通过正圆锥体轴线时,截交线为(D )0A.矩形B.椭圆C.双曲线加直线D.等腰三角形8.当截平面垂直于正圆锥体轴线时,截交线为(B )。
A.矩形B.圆C.椭圆D.等腰三角形9.平面切割圆球时,截交线为(C )oA.矩形B.椭圆C.圆D.正方形10.两圆柱体垂直相交产生一条封闭的(B )曲线。
A.平面B.空间C.平行D.相交11.当正交两圆柱的相对位置不变,而相对大小发生变化时,相贯线的(CA,形状和位置将没有变化 B.形状变化,位置不变C.位置变化,形状不变D.形状和位置将随之变化4.2按要求完成下列各题一、截交线和相贯线基础知识填空题1.平面截割立体而产生的表面交线称为截交线。
2.截交线具有以下两个基本特性:截交线为一封闭—的平面图形;截交线是截平面与立体表面的共有线。
3.平面截割圆柱体时,当截平面与圆柱轴线平行,截交线为矩形;当截平面与圆柱轴线垂直,截交线为一趴形;当截平面与圆柱轴线倾斜,截交线为椭圆形。
4.两圆柱体相交,其交线称为相贯线。
5.两圆柱体的相贯线,实际上是两圆柱体表面上一系列一亚二点的连接。
一般情况下为一封胆的空间曲线。
6.两个同轴回转体相交时,它们的相贯线一定是垂直于轴线的」a7.平面切割圆球时,其交线均为圆。
相贯线练习题
一、单项选择题(每题8分)
1.等直径圆柱相贯,其相贯线形状为。
()
A.平面圆
B.两个正交的椭圆
C.45°直线
D.双曲线
2.如图所示,下列左视图正确的是。
()
3.下图所示,相贯线画法错误的是________。
()
4.根据主、俯视图(如图所示),正确的左视图是。
()
5.根据主俯视图(如图所示),选择正确的左视图。
()
二、是非选择题(每题10分)
6.立体被平面截切所产生的表面交线称为相贯线,两立体相交所产生的表面交线称为截交线。
()
7.立体表面交线的基本性质是封闭性和共有性。
()
8.影响相贯线变化的因素有相交立体的大小变化、相交立体的相对位置变化和相交立体的表面形状变化。
()
三、作图、分析、计算题
9.补画图中的缺线。
(10分)
10补画图中的缺线。
(20分)。
圆锥截交线习题及答案圆锥截交线习题及答案圆锥截交线是数学中的一个重要概念,它描述了在一个圆锥体上截取的平面与圆锥体的交线形状。
在几何学中,圆锥截交线的研究可以帮助我们更好地理解空间几何关系。
下面将介绍一些常见的圆锥截交线习题及其答案。
一、直截圆锥体的底面是一个直径为8cm的圆,截锥体的高为10cm,求截取圆锥体的平面与底面圆的交线长度。
解答:首先,我们可以根据圆锥体的性质得知,截取圆锥体的平面与底面圆的交线是一个圆。
由于底面圆的直径为8cm,那么半径r=8/2=4cm。
根据勾股定理,可以得到截取圆锥体的平面与底面圆的交线长度h的平方等于斜边的平方减去底边的平方,即h²=10²-4²=100-16=84。
所以,交线的长度h≈√84≈9.17cm。
二、直截圆锥体的底面是一个直径为10cm的圆,截锥体的高为12cm,求截取圆锥体的平面与底面圆的交线的周长。
解答:同样地,截取圆锥体的平面与底面圆的交线是一个圆。
底面圆的直径为10cm,那么半径r=10/2=5cm。
根据圆的周长公式C=2πr,可以得到交线的周长C≈2π×5≈31.42cm。
三、直截圆锥体的底面是一个半径为6cm的圆,截锥体的高为8cm,求截取圆锥体的平面与底面圆的交线的面积。
解答:同样地,截取圆锥体的平面与底面圆的交线是一个圆。
底面圆的半径为6cm,那么圆的面积公式A=πr²,可以得到交线的面积A≈π×6²≈113.1cm²。
四、直截圆锥体的底面是一个半径为8cm的圆,截锥体的高为10cm,求截取圆锥体的平面与底面圆的交线与底面圆的交线的夹角。
解答:我们可以利用三角函数来求解这个问题。
根据圆锥体的性质,截取圆锥体的平面与底面圆的交线与底面圆的交线的夹角为θ。
根据正弦定理,可以得到sinθ=交线长度h/底面圆的直径=9.17/8≈1.15。
由于夹角θ的范围为0°到180°,我们可以使用反正弦函数求解,即θ=sin^(-1)(1.15)≈49.5°。