截交线练习题

机械制图练习题库+参考答案一、单选题（共26题，每题1分，共26分）1.某调整螺旋，采用双线粗牙螺纹，螺距为3mm，为使螺母相对螺杆沿轴向移动12mm，螺杆应转()圈。

A、2B、3C、4D、2.5正确答案：A2.机械图样中，表示可见轮廓线采用()。

A、波浪线B、粗实线C、细实线D、细点画线正确答案：B3.截平面与立体表面的交线称为（）A、截交线B、相贯线C、相交线D、以上都不是正确答案：A4.仰视图是（）。

A、由后向前投影B、由前向后投影C、由上向下投影D、由下向上投影正确答案：D5.产品用放大一倍的比例绘图，在标题栏比例项中应填（）。

A、1:2B、放大一倍C、1×2D、2:1正确答案：D6.制图国家标准规定，字体的号数，即是字体的()。

A、宽度和高度B、宽度C、长度D、高度正确答案：D7.具有间隙的配合称为（）。

A、过渡配合B、间隙配合C、不明确性质D、过盈配合正确答案：B8.三投影面体系中的三个投影面互相（）A、垂直B、倾斜C、交叉D、平行正确答案：A9.Φ50+0.025表示()A、实际尺寸是Φ50㎜B、基本尺寸是Φ50㎜C、最大尺寸是Φ50㎜D、最小尺寸是Φ50.025正确答案：B10.画断面图时，若由两个或多个相交剖切平面剖切得出的移出断面，中间应用（）断开为两个图形。

A、波浪线B、点画线C、虚线D、粗实线正确答案：A11.已知某个几何体的主视图、左视图和俯视图分别为长方形、长方形、圆，则该几何体是（）。

A、球体B、圆柱体C、圆锥体D、长方体正确答案：B12.点的正面投影和侧面投影的连线（）。

A、垂直于oz轴B、平行于ox轴C、垂直于OY轴D、垂直于ox轴正确答案：A13.重合断面的轮廓用（）画出。

A、波浪线B、粗实线C、细实线D、点划线正确答案：C14.Α3图纸的大小为（）。

A、841×594B、420×297C、210×297D、841×595正确答案：B15.不可见轮廓线采用（）来绘制。

截交线习题截交线习题1. 完成平面立体被平面截切后的侧面投影2. 完成五棱柱被二平面截切后的侧面投影3 完成四棱锥被平面截切后的三面投影4. 完成四棱锥被平面截切后的三面投影5. 求平面立体的截交线6. 画出穿孔六棱柱被截切后的水平投影，并补全其侧面投影截交线习题7.完成圆柱被平面截切后的侧面投影8. 完成圆柱被平面截切后的水平投影9. 完成立体被平面截切后的水平投影10.补画出立体的侧面投影11. 补画立体的侧面投影12. 补画立体的侧面投影13. 补画立体的侧面投影14. 求作回转体第三视图15. 求截交线16. 补画侧面投影17. 已知圆柱开一个正方形的孔，补画左视图18. 补画圆柱开槽后的正面投影19. 补全左视图中所缺的线条20. 完成圆锥被平面截切后的水平投影和侧面投影21. 求圆锥的截交线22.补画带缺口圆锥的侧面投影，并补全其水平投影。

23. 补全圆锥截断体的三面投影24. 补全俯视图，并完成左视图。

25. 补全圆球穿方孔的三面投影26. 完成半球被平面截切后的水平投影和侧面投影27. 完成半球被平面截切后的水平投影和侧面投影28. 求圆球的截交线29. 作出半球开槽后的H面及W面投影30. 完成左视图，画出俯视图31. 完成立体被平面截切后的水平投影32. 完成立体被平面截切后的水平投影33. 完成立体被平面截切后的水平投影34. 求组合体的截交线35. 作立体切割后的水平投影和侧面投影36. 求作截切后立体的侧面投影37. 补画圆球和圆柱组合体开槽后的水平和侧面投影38. 补画水平投影及侧面投影漏线39. 完成穿孔圆柱被截切后的水平投影40. 完成立体的水平投影。

SUMMAR Y
一款专门用于有限元分析的三维 CAD软件，可以进行高质量的三 维建模。
使用三维软件绘制截交线
打开三维建模软件，新建一个 空白文档。
使用软件的绘图工具，根据截 交线的形状和尺寸进行绘制。
根据需要，对截交线进行必要 的修改和调整，确保其符合实 际需求。
保存并导出三维模型，以便后 续应用和展示。
三维模型的应用与展示
REPORT
CATALOG
DATE
ANALYSIS
SUMMARY
机械制图——截交 线(平面切割平面体) 课件
目录
CONTENTS
• 截交线的基本概念 • 平面切割平面体的截交线 • 实际应用中的截交线 • 截交线的三维建模 • 截交线的实际操作练习
REPORT
CATALOG
DATE
ANALYSIS
REPORT
CATALOG
DATE
ANALYSIS
SUMMAR Y
05
截交线的实际操作练习
练习题一：绘制正方体的截交线
总结词
掌握正方体截交线的绘制方法
详细描述
通过平面切割正方体，观察截交线的形状和特点，掌握绘制正方体截交线的基本步骤和 技巧。
练习题二：绘制长方体的截交线
总结词
熟悉长方体截交线的绘制技巧
02
平面切割平面体的截交 线
正方体的切割
正方体在平面切割时，其截交线可能 是一个点、一条直线或一个平面多边 形。根据切割面的位置和角度，截交 线的形状会有所不同。
当切割面与正方体的一个面平行时， 截交线是一条直线；当切割面与正方 体的棱线平行时，截交线是一个平面 多边形；当切割面与正方体的顶点相 交时，截交线是一个点。

圆锥截交线习题及答案圆锥截交线习题及答案圆锥截交线是数学中的一个重要概念，它描述了在一个圆锥体上截取的平面与圆锥体的交线形状。

在几何学中，圆锥截交线的研究可以帮助我们更好地理解空间几何关系。

下面将介绍一些常见的圆锥截交线习题及其答案。

一、直截圆锥体的底面是一个直径为8cm的圆，截锥体的高为10cm，求截取圆锥体的平面与底面圆的交线长度。

解答：首先，我们可以根据圆锥体的性质得知，截取圆锥体的平面与底面圆的交线是一个圆。

由于底面圆的直径为8cm，那么半径r=8/2=4cm。

根据勾股定理，可以得到截取圆锥体的平面与底面圆的交线长度h的平方等于斜边的平方减去底边的平方，即h²=10²-4²=100-16=84。

所以，交线的长度h≈√84≈9.17cm。

二、直截圆锥体的底面是一个直径为10cm的圆，截锥体的高为12cm，求截取圆锥体的平面与底面圆的交线的周长。

解答：同样地，截取圆锥体的平面与底面圆的交线是一个圆。

底面圆的直径为10cm，那么半径r=10/2=5cm。

根据圆的周长公式C=2πr，可以得到交线的周长C≈2π×5≈31.42cm。

三、直截圆锥体的底面是一个半径为6cm的圆，截锥体的高为8cm，求截取圆锥体的平面与底面圆的交线的面积。

解答：同样地，截取圆锥体的平面与底面圆的交线是一个圆。

底面圆的半径为6cm，那么圆的面积公式A=πr²，可以得到交线的面积A≈π×6²≈113.1cm²。

四、直截圆锥体的底面是一个半径为8cm的圆，截锥体的高为10cm，求截取圆锥体的平面与底面圆的交线与底面圆的交线的夹角。

解答：我们可以利用三角函数来求解这个问题。

根据圆锥体的性质，截取圆锥体的平面与底面圆的交线与底面圆的交线的夹角为θ。

根据正弦定理，可以得到sinθ=交线长度h/底面圆的直径=9.17/8≈1.15。

由于夹角θ的范围为0°到180°，我们可以使用反正弦函数求解，即θ=sin^(-1)(1.15)≈49.5°。

9′10′
10〞 3〞8〞
4′3′
7′8′
9〞 4〞7〞
10 3 2 8 6
1 4 9
5 7
整理棱线投影
6 1
4
3
2
5
求正四棱锥被截切后的水平和侧面投影。 1、空间分析
6′ 5′7′ 4′8′ 1′ 3′9′ 2′10′ 10 10″ 9″ 6″ 7″ 8″ 4″ 2″ 1″ 3″ 5″
立体表面交线的形状？ ——空间10边形
2、投影分析
截交线的正面投影落 在截平面的积聚性投影上；
——水平截平面截切的交 线平行于四棱锥对应底边；
2、投影分析
截平面为正垂面，截 交线的正面投影落在截平 面的积聚性投影上，要求 的是截交线的水平投影和 侧面投影。
2 1
3 4
3、投影作图 4、整理图线
5
采用的是哪种解题方法？
完成棱柱体被截切后的水平投影和侧面投影。
6′7′ 4′5′ 7″ 6″ 4″
1、空间分析：
截交线为平面几边形？ ——平面七边形
截交线的重要例题
B0
C0
[例题4]： 作出四 棱锥被 截切后
A0
C
D0
D
b ( d ) a
c
A
B
的水平
投影， 并求截 断面的 实形。
（1）找交点； （2）依次连接各点；
d
（3）判别可见性； （4）整理棱线；
c
a
b
（5）求实形；
作出四棱柱被截切后的水平投影和侧面投影，并出求 截断面的实形。
9 8 4
3
7
6 1 5 2
——侧平截平面截切的交 线平行于四棱锥前后棱线。

★求截交线
★完善圆柱轮廓
结果和立体图
3′(4′) 1′(2′)
●
4(2)
●
●
3(1)
4″ 2″
●
●
3″ 1″
●
●
4
●
2●
3
●
1 ●
测试题2：空心圆柱上部开有长方槽，若已
知其V、H投影，试求W投影。
测试题2：空心圆柱上部开有长方槽，若已
知其V、H投影，试求W投影。
一、平面与圆锥相交所得截交线形状
多个平面截切立体时， 确定截交线形状为矩形和圆弧。
要分别对各截平面进行 截交线的分析和作图。
2)分析圆柱体轮廓素线的投影。 3)求截交线。
[例题4 ] 求圆柱截交线
1'2'
2"
3'4'
4"
24
1" 3"
解题步骤
1 分析 截交线的水平投影为直 线和部分圆，侧面投影为矩形 ；
2 求出截交线上的特殊点Ⅰ、 Ⅱ、Ⅲ、Ⅳ；
1(2)
2" ●
● 1"
3(4)
2(4)
注意：
要逐个截平面分析和绘制
截交线。当平面体只有局
部被截切时，先假想为整
体被截切，求出截交线后
1(3)
再取局部。
测试题: 求八棱柱被平面P截切后的俯视图。
P
4（5）
2(3、6、7)
5 7
6 3
4 2
1(8)
8
7
5 6
3 4
1
2
8
1
7 8
54 63 2
1
例1、求如图所示三棱锥被正垂面所截切，求作截交线的水平

截一个几何体作业同步练习(一)
一、填一填
1．一个平面与另一个平面相交，它们的交线是一条线，如果一个平面和另一个曲面相交，它们的交线是。

2．一个又大又圆的西瓜，用刀从中间切下去，切面是。

3．用一个平面去截一个圆柱，截面可能的形状是。

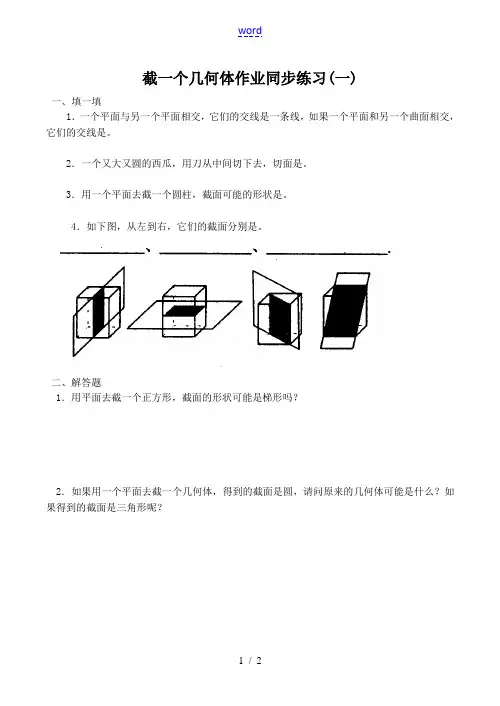
4．如下图，从左到右，它们的截面分别是。

二、解答题
1．用平面去截一个正方形，截面的形状可能是梯形吗？
2．如果用一个平面去截一个几何体，得到的截面是圆，请问原来的几何体可能是什么？如果得到的截面是三角形呢？
三、做一做
1．用一个平面去截一个圆锥，请画出截面可能出现的图形。

2．请指出下列各图形中的截面图形的名称，并画出起截面图。

四、想一想
1．如果用一个平面去截一个几何体，得到的截面是下面的图形，你知道被截的是一个什么样的几何体？。

1 ' 6
b
1" 4 8
d
5．整理轮廓线。
1
a c
2
7 5 3
[例题2]求圆球截交线 例题2] 2]求圆球截交线
1' 2' 3' 2"
解题步骤
3"
1．分析 截平面为两个 侧平面和一个水平面， 截交线为圆弧和直线的 组合；截交线的水平投 影和侧面投影均为圆弧 和直线的组合； 2．求出截交线上的特殊 点Ⅰ、 Ⅱ； 3．求出各段圆弧；
1
2 3
4．判别可见性，整理轮 廓线。
[例题3]求圆球截交线 例题3] 3]求圆球截交线
[例题4]分析并想象出圆球穿孔后的投影 例题4] 4]分析并想象出圆球穿孔后的投影
五、综合题
[例题1]分析并想象出物体的投影 例题1] 1]分析并想象出物体的投影
[例题2]求出物体切割后的投影 例题2] 2]求出物体切割后的投影
1'2' 2" 1"
解题步骤 1 分析 截交线的水平投影为 直线和部分圆，侧面投影为矩 形；
3'4'
4"
3"
2 求出截交线上的特殊点 Ⅰ 、 Ⅱ、Ⅲ、Ⅳ； 3 顺次地连接各点，作出截交 线并判别可见性； 4 整理轮廓线。
24
13
[例题5]求圆柱截交线 例题5] 5]求圆柱截交线
1' 4' 5' 3' 2' 2"
[例题1]求圆球截交线 例题1] 1]求圆球截交线
2'
c'd'
7' 8' 3'4' 5'6'

截一个几何体作业同步练习(一)
一、填一填
1．一个平面与另一个平面相交，它们的交线是一条线，如果一个平面和另一个曲面相交，它们的交线是。

2．一个又大又圆的西瓜，用刀从中间切下去，切面是。

3．用一个平面去截一个圆柱，截面可能的形状是。

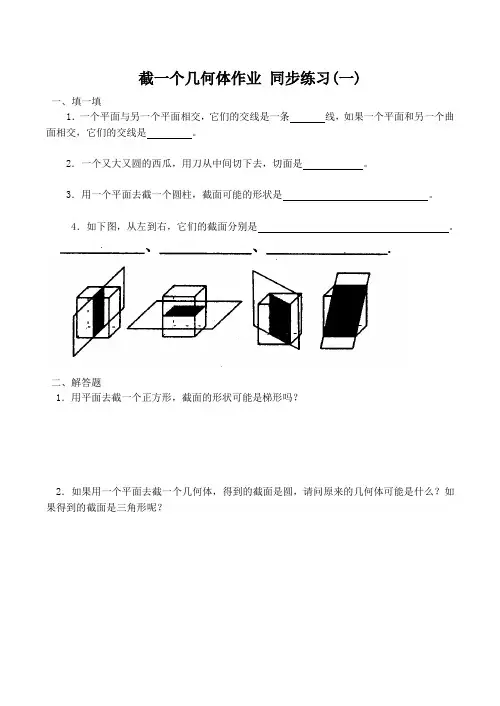
4．如下图，从左到右，它们的截面分别是。

二、解答题
1．用平面去截一个正方形，截面的形状可能是梯形吗？
2．如果用一个平面去截一个几何体，得到的截面是圆，请问原来的几何体可能是什么？如果得到的截面是三角形呢？
三、做一做
1．用一个平面去截一个圆锥，请画出截面可能出现的图形。

2．请指出下列各图形中的截面图形的名称，并画出起截面图。

四、想一想
1．如果用一个平面去截一个几何体，得到的截面是下面的图形，你知道被截的是一个什么样的几何体？。