上海交大杜秀华老师《现代控制理论》第四章 线性系统的能控性和能观性6
- 格式:doc
- 大小:1.67 MB
- 文档页数:31

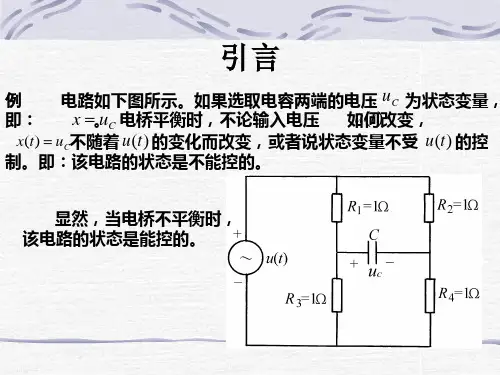
第4章(1)线性控制系统的能控性和能观性第四章线性控制系统的能控性和能观性在现代控制理论中,能控性(Controllability)和能观性(Observ- ability)是两个重要的概念,它是卡尔曼(Kalman)在1960年提出的,是最优控制和最优估计的设计基础。
能观(测)性针对的是系统状态空间模型中的状态的可观测性,它反映系统的内部状态x(t)(通常是不可以直接测量的)被系统的输出量y(t)(通常是可以直接测量的)所反映的能⼒。
能控性严格上说有两种,⼀种是系统控制输⼊u(t)对系统内部状态x(t)的控制能⼒,另⼀种是控制输⼊u(t)对系统输出y(t)的控制能⼒。
但是⼀般没有特别指明时,指的都是状态的可控性。
所以,系统的能控性和能观性研究⼀般都是基于系统的状态空间表达式的。
4-1 线性连续定常系统的能控性定义对于单输⼊n 阶线性定常连续系统bu Ax x+= 若存在⼀个分段连续的控制函数u(t),能在有限的时间段 []f t t ,0内把系统从0t 时刻的初始状态()0t x 转移到任意指定的终态()f t x ,那么就称系统在0t 时刻的状态()0t x 是能控的;如果系统每⼀个状态()0t x 都能控,那么就称系统是状态完全可控的。
反之,只要有⼀个状态不可控,我们就称系统不可控。
对于线性定常连续系统,为简便计,可以假设00=t ,()0=f t x ,即00=t 时刻的任意初始状态()0x ,在有限时间段转移到零状态()0=f t x (原点)。
4-2线性连续定常系统的能控性判别4-2-1具有约旦标准型系统的能控性判别 1.单输⼊系统具有约旦标准型系统bu x x+Λ==Λn λλλλ0000000000000321n λλλλ≠≠≠≠ 321即为n 个互异根或bu Jx x+==++n m m J λλλλλλ000000000000000100000000121111m 个重根1λn-m 个互异根n m m λλλ≠≠≠++ 21 例:分析下列系统的能控性(1)u b x x+??=221000λλ[]x c c y 21=解:?=111x xλ 1x 与u ⽆关,即不受u 控制 ?+=u b x x2222λ 2x 为能控状态该系统为状态不完全能控,因⽽为不能控系统。





上海交⼤杜秀华⽼师《现代控制理论》第四章线性系统的能控性和能观性6三、多输⼊多输出系统的标准形旺纳姆(Wonham )标准形和龙伯格(Luenberger )标准形。
1.多输⼊多输出系统的能控标准形考虑线性定常系统:Σx Ax Bu y Cx=+=x 为n 维状态向量,u 为p 输⼊向量,y 为q 维输出向量如果系统能控,则系统的能控性矩阵的秩为n ,即cQ 中有n 个线性⽆关列。
111121212[]c Q b b b Ab Ab Ab A b A b A b n n n p p p ---=对多输⼊系统,1p >,c Q 中有np 列,所以,在c Q 中可以找出很多种n 个线性⽆关列的情况。
这⾥介绍两种寻找n 个线性⽆关列的⽅法,以构成状态变换阵,将状态空间描述形式变换为旺纳姆能控标准形和龙伯格能控标准形。
定理 [旺纳姆能控标准形]对完全能控的线性定常系统,存在线性⾮奇异变换1x Px Q x -==使状态空间表达式转化为旺纳姆能控标准形:Σx A x B u y C xcW c c c =+=式中111211222A A A 0A A A Q AQ 00A m m c mm -??==111010011,2,,0001A ,i i ii i mννννααα?-??==---)112()00,1,,00A i j ij ij ij ij j i m νννγγγ==+1(1)11(1)001001B Q B m p c n m np ββββ+-+==????C CQ c =(⽆特殊形式)证明:见书例求如下系统的旺纳姆能控标准形121100*********A B -==计算系统的能控性矩阵2101204010101001042BABA B c Q ??==3c Q rank =,系统完全能控。
按2111{,,} b A b A b 和2222{,,} b Ab A b 搜索,可知112,,b Ab b 是线性独⽴的。


第4章“线性系统的能控性与能观性”习题与解答4.1 判断下列系统的能控性。
1) u x x x x⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡10 01112121 2) ⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡21321321111001342100010u u x x x x xx3) ⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡21321321020011 10030013u u x x x x xx解:1) 由于该系统控制矩阵⎥⎦⎤⎢⎣⎡=01b ,系统矩阵⎥⎦⎤⎢⎣⎡=0111A ,所以 ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=1101 0111Ab 从而系统的能控性矩阵为[]⎥⎦⎤⎢⎣⎡==1011Ab bU C 显然有[]n Ab bU C ===2rank rank满足能控性的充要条件,所以该系统能控。
2)由于该系统控制矩阵为100111B ⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦系统矩阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=342100010A 则有,0101001001 01112431117AB ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥==-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-----⎣⎦⎣⎦⎣⎦ 20100111001 111724317115A B -⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=-=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥----⎣⎦⎣⎦⎣⎦从而系统的能控性矩阵为21001110111171117115C U BABA B -⎡⎤⎢⎥⎡⎤==--⎣⎦⎢⎥⎢⎥--⎣⎦有n U C ==3rank满足能控性的充要条件,所以该系统能控。
3)由于该系统控制矩阵为110020B -⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦系统矩阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=10030013A 则有,3101133030 00000012020AB ---⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=-=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦ 23103399030 0000012020A B ---⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=-=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦于是,系统的能控性矩阵为21133990000002220C U BABA B ---⎡⎤⎢⎥⎡⎤==⎣⎦⎢⎥⎢⎥-⎣⎦可知n U C <=2rank不满足能控性的充要条件,所以该系统不完全能控。


三、 多输入多输出系统的标准形旺纳姆(Wonham )标准形和龙伯格(Luenberger )标准形。
1.多输入多输出系统的能控标准形考虑线性定常系统:Σx Ax Bu y Cx=+=x 为n 维状态向量,u 为p 输入向量,y 为q 维输出向量如果系统能控,则系统的能控性矩阵的秩为n ,即cQ 中有n 个线性无关列。
111121212[]c Q b b b Ab Ab Ab A b A b A b n n n p p p ---=对多输入系统,1p >,c Q 中有np 列,所以,在c Q 中可以找出很多种n 个线性无关列的情况。
这里介绍两种寻找n 个线性无关列的方法,以构成状态变换阵,将状态空间描述形式变换为旺纳姆能控标准形和龙伯格能控标准形。
定理 [旺纳姆能控标准形]对完全能控的线性定常系统,存在线性非奇异变换1x Px Q x -==使状态空间表达式转化为旺纳姆能控标准形:Σx A x B u y C xcW c c c =+=式中111211222A A A 0A A A Q AQ 00A m m c mm -⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎣⎦11(11(1)11010011,2,,0001A ,i i ii i mννννααα⨯-⎡⎤⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥---⎢⎥⎣⎦)112()00,1,,00A i j ij ij ij ij j i m νννγγγ⨯⎡⎤⎢⎥⎢⎥==+⎢⎥⎢⎥⎢⎥⎣⎦1(1)11(1)001001B Q B m p c n m np ββββ+-+⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦C CQ c =(无特殊形式)证明:见书 例 求如下系统的旺纳姆能控标准形121100*********A B -⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦计算系统的能控性矩阵2101204010101001042BABA B c Q ⎡⎤⎢⎥⎡⎤==⎣⎦⎢⎥⎢⎥⎣⎦3c Q rank =,系统完全能控。
按2111{,,} b A b A b 和2222{,,} b Ab A b 搜索,可知112,,b Ab b 是线性独立的。
得1,221==νν。
21111121211111121100110,0,0,000014410A b Ab b b Ab A b αααα=--⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥====--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦解得 441211=αα,=-111111121e b Ab e b α=+=得111212121131040000101100e e b e b -⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=-+=====⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦由22111211112212-Ab b e e αγγ=++,即21121122203111000010αγγ-⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=-++⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦解得 20,121==-=122121 , γγα由此可得1111122201000-44210000101A A A Q AQ B Q B A c c --⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥=====⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎣⎦⎣⎦式中,变换矩阵为 310001100Q -⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦系统的旺纳姆能控标准形为011004421000101x x u ⎡⎤⎡⎤⎢⎥⎢⎥=-+⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦龙伯格能控标准形相对于旺纳姆能控标准形在系统极点配置中应用更广,这是由于在构成状态变换阵时,相对均衡地考虑了各个输入的作用。
考虑线性定常系统:Σx Ax Bu y Cx=+=x 为n 维状态向量,u 为p 输入向量,y 为q 维输出向量。
如果系统完全能控,设矩阵B 的列线性无关,这在实际上通常总能成立,或可进行处理获得,b i 为B 的第i 列,那么,系统的能控性矩阵c Q 可表示为111121212[]c Q b b b Ab Ab Ab A b A b A b n n n p p p ---=对上式从左到右依次找出n 个线性无关列,即若某个列不能表示成其左边各线性独立列的线性组合就为线性无关列,否则为线性相关列。
考虑到c Q 的组成特点,如果,1,2,,A b i m m p = 和其左边线性独立列线性相关,则1Ab i m+也和其左边线性独立列线性相关,又由于假设B 为满秩,则可将此搜索结果重新排列,并组成非奇异矩阵P :121111111222P b Ab A b b Ab A b b Ab A b pp p p μμμ----⎡⎤=⎣⎦式中,n p =+++μμμ 21, },,{21p μμμ 为系统能控性指数集。
对定义1P -矩阵求逆,并表示成分块矩阵形式:1111111()e e P P e e pTT T p T p μμ--⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦式中,块的行数为,1,2,,i i p μ= 。
再在矩阵P 中,取出各个块矩阵的末行,即为1212,,,e e e pT T T p μμμ ,并按如下方式构造变换矩阵P cL:111111111e e A e A P e e A e A p pppTTT cLT p Tp Tp μμμμμμμμ--⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦定理[龙伯格能控标准形]对完全能控的线性定常系统,存在线性非奇异变换1ˆxP x Q x cL cL -== 使状态空间表达式转化为龙伯格能控标准形ˆˆˆˆ:ˆˆΣx A x B u y Cx cL c cc=+= 1112112122212ˆˆˆˆˆˆˆˆˆˆA A A A A A A Q AQ A AA pp c cL cL p p pp -⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎣⎦(01001ˆ1,2,,0001***A ,i i ii i p μμ⨯⎡⎤⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦)()00ˆ,,,1,2,,000***A i j iji j i j p μμ⨯⎡⎤⎢⎥⎢⎥=≠=⎢⎥⎢⎥⎣⎦1001**ˆ001B Q B c cL-⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦ˆC CQ c cL =(无特殊形式)*表示可能的零元或非零元。
证明:从略。
例 求如下系统的龙伯格能控标准形1000303110114101101000A B ⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥==⎢⎥⎢⎥--⎢⎥⎢⎥-⎣⎦⎣⎦计算系统的能控性矩阵c Q223312121212000114413100331010300114413135100011339c Q b b Ab Ab A b A b A b A b =⎡⎤⎣⎦⎡⎤⎢⎥-----⎢⎥=⎢⎥⎢⎥-----⎣⎦ 式中,21212,,,b b Ab A b 线性无关,所以,系统完全能控,且11μ=,23μ=。
由此构成矩阵1P -,并求其逆阵P 。
121212001410310014130013P b b Ab A b -⎡⎤⎢⎥--⎢⎥==⎡⎤⎣⎦⎢⎥⎢⎥--⎣⎦1102101330041001P -⎡⎤⎢⎥-⎢⎥=⎢⎥--⎢⎥⎣⎦将P 分为两个块阵,第一个块的行数为1,第二个块的行数为3。
取出P 中的第一行11e T 和第四行23e T,组成变换矩阵P cL ,并求其逆阵Q cL 。
1123232231102100110000010e eP e A e A T T cL T T -⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦10010123000010110Q P cL cL -⎡⎤⎢⎥-⎢⎥==⎢⎥⎢⎥-⎣⎦由此可求出系统的龙伯格能控标准形为1101010001000ˆˆ000100113401A Q AQ B Q B=c cL cLc cL--⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦2.多输入多输出系统的能观标准形利用能观性和能控性的对偶关系,可以方便地得出完全能观系统的旺纳姆能观标准形和龙伯格能观标准形。
定理 [旺纳姆能观标准形]对完全能观的线性定常系统,存在线性非奇异变换1xP x Q x o o -== 使状态空间表达式转化为旺纳姆能控标准形:Σx A x B u y Cx oW o oo=+= 式中111212212A A A A P AP A AA o o ol l ll -⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎣⎦1101001,1,2,,0001A i ii i i lγαα-⎡⎤⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦1200,1,,,1,2,,00A i ij ij ij iji j l j l νςςς⎡⎤⎢⎥⎢⎥==+=⎢⎥⎢⎥⎢⎥⎣⎦1B P B o o-= (无特殊形式) (1)1(1)1010101C CP o o l l n p pn ββββ++⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦定理 [龙伯格能观标准形]对完全能观的线性定常系统,存在线性非奇异变换1x P x Q x o o -==使状态空间表达式转化为龙伯格能控标准形:Σx A x B u y C xoL o o o =+=式中1112121221112A A A A A A A P AP A A A q q o oL oL q q qq -⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎣⎦0*1001,1,2,,00001*A ii i q⎡⎤⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦00*00*,00*A ij i j ⎡⎤⎢⎥⎢⎥=≠⎢⎥⎢⎥⎣⎦1B P B o oL -= (无特殊形式)01**01C CP o oL ⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦能观标准形在系统观测器设计中有重要应用。
应该指出,单变量系统的传递函数与能控标准形和能观标准形的参数有明显的关系。
已知传递函数可直接写出系统的能控标准形和能观标准形,不必求出变换矩阵,反之,由标准形也可以直接写出传递函数。
但在多变量系统中,不存在这样的对应关系,必须求出变换矩阵,才能求出标准形。
4.7 线性系统的结构分解介绍如何通过非奇异变换,将系统的状态空间描述按能控性和能观性进行结构分解。
通过状态空间描述的结构分解可以建立状态空间描述和系统传递函数之间的关系,为最小实现问题的提出提供理论依据。
状态空间描述的结构分解在系统综合状态反馈和系统镇定问题中也有重要作用。
一、 按能控性的系统结构分解按能控性分解是通过线性非奇异变换,将系统的完全能控状态和不能控状态,以明显的方式区分开来表示。
考虑线性定常系统:Σx Ax Bu y Cx=+=式中,x 为n 维状态向量,u 为p 输入向量,y 为q 维输出向量。