三坐标测量机不确定度分析与检测能力评价

测 量 不 确 定 度 报 告47BQD-01-20171目的为了验证产品角度尺寸与设计值的符合性，需要对产品的角度尺寸进行测量，三坐标测量机测量分辨率高是一种有效的测量设备。

根据JJF1059.1-2012《测量不确定度评定与表示》对三坐标测量机的角度测量进行测量不确定度评定。

2依据GB/T3177-2009 产品几何技术规范（GPS)光滑工件尺寸的检验 3适用范围用单一材料或层积材料制成的有一定刚性的产品，产品尺寸在设备测量范围以内。

4方法概要采用三坐标测量机对任意工件（本例中采用二级角度40°量块）在标准环境（温度20±2℃，湿度＜65％）中，进行测量，在直角坐标系空间的有效量程上，记录三坐标测量机示值，各机器平面测量三次，得到9组读数，将读数作为测量结果。

5数学模型由测量的方式，建立数学模型如下：（采用40°的量块）i i T M = （i ＝1,2…9）式中：i M ——测量结果，i T ——三坐标测量机的读数 6使用的计量器具、标准物质和仪器设备① 三坐标测量机，该设备的分辨率为0.5μm ，假定三角分布，k ＝61/2 ② 三坐标测量机，该设备的校准证书指出最大允许示值误差（MPE E ）为 8.0+7.5L/1000 (μm ) ，在本例中L ≤70mm ，得MPE E =8.525μm ，假定均匀分布，k ＝31/2；③ 三坐标测量机，该设备的校准证书指出最大允许探测误差（MPE P ）为8.0μm，假定均匀分布，k＝31/2。

④三坐标测量机，该设备说明中设备轴间垂直度允差为0.0005°，假定为均匀分布，k=31/2。

7测量结果M及典型值用40°角度量块进行9次测量结果如下：XY面YZ面ZX面读数1 读数2 读数3 读数4 读数5 读数6 读数7 读数8 读数9 40.0014 39.9987 40.0025 39.9995 40.0009 39.9971 39.9988 39.9980 39.9991 平均值： 39.9996°8不确定度分量的识别、分析和量化按照数学模型及方法概要，其不确定度来源有5方面：① M的测量重复性u1 (M)（8.1）②三坐标测量机的分辨率引入的标准不确定度u2 (M)（8.2）③三坐标测量机的最大允许示值误差引入的标准不确定度u3 (M)（8.3）④三坐标测量机的最大允许探测误差引入的标准不确定度u4(M)（8.4）⑤三坐标测量机的轴间垂直度允差引入的标准不确定度u(M) (8.5)58.1 测量重复性u1(M)用40°角度量块进行9次测量重复性，贝塞尔公式计算单次测量标准差s(M)=[∑M i2/(n-1)]1/2= 0.001726°u1(M)＝s(M)/ 91/2＝ 0.0005754°8.2 设备的分辨率引入的标准不确定度u2(M)考虑设备在根据测点构造矢量时，因设备的示值误差±0.5μm会发生角度偏差，在L=70的长度内，设测点间距为60mm，角误差即为±0.0009549°，双矢量则为：±0.001910°,假定为三角分布，k＝61/2，u2(M)＝0.001910°/61/2=0.0007797°8.3 设备的最大允许示值误差引入的标准不确定度u3(M)设备的最大允许示值误差是MPE E=8.525μm, 同样在L=70的长度内，设测点间距为60mm，角误差即为：0.01628°，双矢量则为：0.03256°，假定均匀分布，k＝31/2u3(M)＝0.03256°/31/2＝0.01880°8.4设备的最大允许探测误差引入的标准不确定度u4(M)设备的最大允许探测误差是MPE P =8μm, 同样在L=70的长度内，设测点间距为60mm，角误差即为：0.01528°，双矢量则为：0.03056°，假定均匀分布，k＝31/2U4(M)＝0.03056°/31/2＝0.01764°8.5设备的轴间垂直度允差为0.0005°，考虑到有三轴存在，彼此无明显相关性，则合成允差为：（0.00052+0.00052+0.00052）1/2=0.0008660°假定为均匀分布，k=31/2U5(M)＝0.0008660°/31/2=0.0005°9计算相对合成标准不确定度u cr(M)符号来源类别量值量序U1(M) 测量重复性A类0.0005754° 1U2(M)设备分辨率B类0.0007797° 2U3(M) 设备示值误差B类0.01880° 3U4(M) 设备探测误差B类0.01764° 4U5(M)垂直度允差B类0.0005° 5u c(M)=[∑u i2(M)]1/2=(0.0005752+0.00077972+0.018802+0.017642+0.00052)1/2=0.02581°10计算扩展不确定U（M）取k＝2，U(M)=2×u c(M)=2×0.02581°=0.05162°11结果完整表达该量块的测量结果M＝39.9996°U（M）＝0.05162°, k=2编制人审核人批准人日期日期日期。

10.16638/ki.1671-7988.2019.21.024浅析测量不确定度评定及在三坐标测量机的应用谢周武（广州汽车集团股份有限公司汽车工程研究院，广东广州511434）摘要：随着科学的进步及对精工极致的追求，测量不确定度评定越来越多的应用于检测实验室，用测量结果及测量结果的不确定度判断零部件某一属性的质量情况。

文章以JJF1059.1-2012《测量不确定度评定与指南》为基础，浅析测量不确定度的定义及评定的一般流程，并以三坐标测量机检测二等标准量块的不确定度评定为例加以描述。

关键词：测量结果；测量不确定度；三坐标测量机中图分类号：U467 文献标识码：B 文章编号：1671-7988(2019)21-70-03The evaluation of measurement uncertainty and its application in CMM are analyzedXie Zhouwu（Guangzhou automotive engineering research institute, Guangdong Guangzhou 511434）Abstract: With the progress of science and the pursuit of the perfection of seiko, the evaluation of measurement uncertainty is more and more applied in testing laboratories. The quality of a component can be judged by the measurement results and the uncertainty of the measurement results. Based on JJF1059.1-2012 measurement uncertainty evaluation and guidelines, this paper analyzes the definition of measurement uncertainty and the general process of evaluation, and describes the uncertainty evaluation of second-class standard gauge block detected by CMM as an example.Keywords: Measurement results; Measurement uncertainty; Coordinate measuring machineCLC NO.: U467 Document Code: B Article ID: 1671-7988(2019)21-70-03前言随着精密测量设备的发展，测量已成为汽车行业发展的重要基础，想要提高产品的的竞争力，就必须改善产品的质量，而改善产品的质量需要通过测量发现产品零部件存在的缺陷和改善的空间。

三坐标测量机测量形位公差不确定度的来源及评定摘要：根据形位公差理论和测量不确定度的相关规范，介绍了用三坐标测量机测量形位公差其不确定度的来源和评定方法，为类似齿轮箱这样机械产品的测量和设计提供一定的参考。

关键词：三坐标测量机；形位公差；不确定度。

1.前言在传统的几何量测量中，得到测量值的准确性高低，很大程度上取决于操作者水平的高低（如经验、操作方法、时间紧迫性等），不可控因素太多。

但随着科学技术发展，对测量技术和测量准确度要求却越来越高，三坐标测量机正是在这样的时代要求背景下出现的，它的出现很大程度上与数控机床的测量需求和计算机技术的迅猛发展有关。

三坐标测量机的发展也非常迅速，从过去的人工操作到现在基本上实现了计算机控制下整个测量过程的自动完成；同时它不仅可以完成各种比较复杂的测量，而且现在还可以实现对数控机床加工的控制。

因此，可以毫不夸张的说，三坐标测量机已经成为现代工业生产和检测中的重要测量设备，广泛地用于机械制造行业等。

三坐标测量机用于零部件的尺寸误差和形位误差的测量，特别是对于形位误差的测量更能显示其高准确度、高效率、测量范围大的优点。

但是在实际测量过程中也经常会出现一些问题，有时可能直接影响到检测结果的准确可靠。

形位公差，国家标准一共规定了包括直线度、平面度、圆度等在内的总计14个项目，由于形位公差项目较多且相互间还存在着一定的包含关系，因此形位公差一直是机械设计、制造与检测中的难点之一。

任何测量都不可避免的具有不确定度，三坐标测量机测量形位公差也不例外。

由于形位公差测量的复杂性，以及三坐标测量机的较高准确性；如何评定三坐标测量机测量形位公差的不确定度，也是摆在我们面前的一道难题。

本文在三坐标测量机测量形位公差不确定度的来源和评定方法等方面进行了较为全面的分析，并提供了一个具体案例供大家参考。

2.三坐标测量机测量形位公差不确定度的来源找出所有影响测量不确定度的因素，即所有的测量不确定度来源是评定测量不确定度的关键一步。

坐标测量机长度测量示值误差不确定度分析1 测量方法依据坐标测量机校准技术规范JJF1064-2000, 坐标测量机的长度测量示值误差是采用量块进行校准, 一般要沿X 轴、Y 轴、Z 轴三个方向和空间四个对角线方向放置量块。

将量块的实际长度与坐标测量机所测的结果进行比较，从而得到坐标测量机的长度测量示值误差。

由于坐标测量机测量空间不同点的测量不确定度不同，不同的测量方案对测量结果的不确定度也有不同的影响，本文讨论坐标测量机自动测量沿空间对角线放置量块的不确定度，并以标称长度为100 mm 和1000 mm 的量块为例估算不确定度，最后得到与标称长度L 有关的扩展不确定度。

2 数学模型δ=R －L （1）式中:δ──坐标测量机的长度测量示值误差； R ──坐标测量机测量量块的读数； L ──对应的量块实际长度。

3 方差和灵敏系数 依:)(][)(222k k m1k c x u x f/y u ∂∂=∑=由式（1）有)()()()()(222222L u L C R u R C u u c c ⋅+⋅=δ=式中C (R )=R ∂δ∂/=1C(L)=L ∂δ∂/-1则 )()(222L u R u u c += （2）由长度测量示值误差的数学模型，根据不确定度的传播公式得到长度测量示值误差的标准不确定度是由坐标测量机读数引起不确定度分量u (R )和量块引起不确定度分量u (L )两大部分组成。

4 不确定度的来源及估算4.1 坐标测量机读数引起不确定度分量u (R )坐标测量机读数引起不确定度主要是坐标测量机的测量重复性。

为了获得测量机沿空间测量的重复性，可将长度为20 mm 的量块沿空间对角线放置，编制测量机检测编程，让测量机自动重复测量该量块10次，得到一组测量误差 x 1,x 2,…,x 10如下表1，按式(3)得到实验标准偏差s, 则u (R )可由式（4）求得。

表1测序 1 2 3 4 5 6 7 8 9 10 误差（μm ） +1.0 +1.3 +1.4 +1.3 +1.6 +1.6 +1.6 +1.4 +1.5 +1.319.0)101(911011012=-=∑∑==i i ii x x s μm （3）u (R )= s （4）4.2 量块引起不确定度分量u (L )4.2.1 由检定量块不确定度引入的不确定度分量u (L 1)首先要根据被校准的坐标测量机最大允许示值误差 MPE E 选择采用量块的等级, 一般来说检定量块不确定度应不超过(MPE E /4)。

三坐标测量机示值校准结果不确定度的评定1. 测量方法（依据JJF1064-2004《坐标测量机校准规范》）尺寸测量校准方法的原理，是通过比较5个不同长度的尺寸实物标准器的校准值和指示值，评价测量尺寸的坐标测量机是否符合规定的最大允许示值误差MPE E 。

5个尺寸实物标准器放在测量空间的7个不同的方向或位置，各测量3次，共进行105次测量。

大值与最小值的。

2. 数学模型对标准器进行测量，得到的测量长度值为E L L L t L L L S S S +∆-∆-∆-∆+=321α其中S L 标准器的校准长度，1L ∆为标准器形状误差等因素引起的误差，2L ∆为长度稳定性引起的误差，3L ∆为测量重复性引起的误差，S α为标准器的热膨胀系数，t ∆为标准器温度对20℃的偏差，E 为坐标测量机的示值L 的误差。

3. 灵敏度系数11/1≈∆+=∂∂=t L L c S S α t L L L c S S ∆=∂∂=/2S S L t L c α=∆∂∂=)(/3 1)(/14-=∆∂∂=L L c1)(/25-=∆∂∂=L L c 1)(/36-=∆∂∂=L L c1/7=∂∂=E L c4. 标准不确定度1u 为标准器校准值S L 的标准不确定度，2u 为标准器热膨胀系数s α的标准不确定度，根据标准器的校准证书确定标准不确定度值。

3u 为标准器温度测量的标准不确定度，由于标准器的温度测量是坐标测量机上的功能，测量误差是坐标测量机示值误差的一部分，与校准方法无关，不予单独考虑。

4u 为标准器的长度变动量引入的标准不确定度。

5u 为标准器的长度稳定度引入的标准不确定度。

6u 为测量重复性引入的标准不确定度。

7u 为坐标测量机示值误差的标准不确定度，也是坐标测量机的测量示值误差的组成部分，与校准方法无关，不予单独考虑。

5. 合成标准不确定度[]2/12625242221)(u u u tu L u u S c +++∆+=。

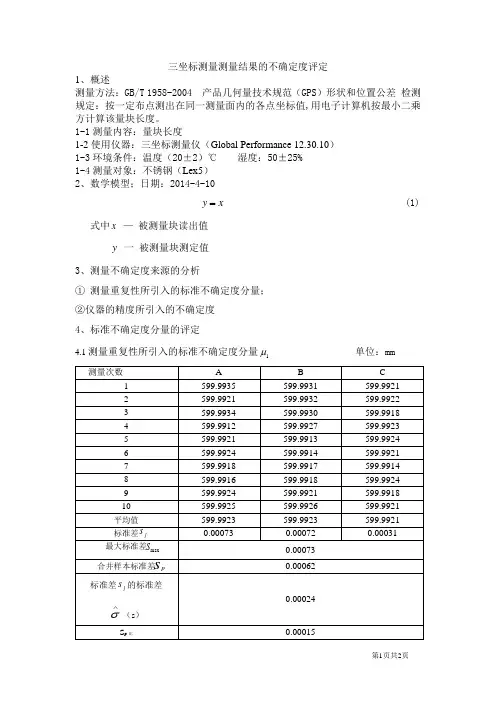
三坐标测量测量结果的不确定度评定1、概述测量方法：GB/T 1958-2004 产品几何量技术规范（GPS）形状和位置公差检测规定：按一定布点测出在同一测量面内的各点坐标值,用电子计算机按最小二乘方计算该量块长度。

1-1测量内容：量块长度1-2使用仪器：三坐标测量仪（Global Performance 12.30.10）1-3环境条件：温度（20±2）℃湿度：50±25%1-4测量对象：不锈钢（Lex5）2、数学模型；日期：2014-4-10y= (1)x式中x—被测量块读出值y一被测量块测定值3、测量不确定度来源的分析①测量重复性所引入的标准不确定度分量；②仪器的精度所引入的不确定度4、标准不确定度分量的评定μ单位：mm4.1测量重复性所引入的标准不确定度分量1合并样本标准差为：∑==mj p s s j m 121 ＝0.62μm （其中m=3）标准差j s 的标准差：1)(12)(-=∑-=∧m j s m j s s σ＝0.24μm)1(2-=n S spP 比＝0.15μm （其中n=10）如≤∧)(s σ S p 比,则可采用合并样本标准差Sp 来评定标准不确定度分量，反之，若子 )(s ∧σ>S p 比，则应采用Sj 中的最大值S max 来评定标准不确定度分量。

所以，1u ＝10/73.0=0.23μm自由度：)1(-=n m pν＝)110(*3-＝274.2仪器的精度所引入的不确定度2u仪器的示值误差为±2.8+3L/1000m μ按均匀分布 k=3 a=2.8+3*600/1000m μ(L 取值600mm)2u =66.23/≈a m μ2221μμ+=U =2266.223.0+=2.75m μ5．扩展不确定度取置信概率P=95%，， k 95=2 扩展不确定度U 95为U 95=k 95）（e U c ⨯=2⨯2.75≈5.51m μ 6．测量结果不确定度报告与表示三坐标测量该量块的长度为599.9922±0.00551mm报告审核： 报告编制：邓过房。

三维坐标测量不确定度分析摘要:文章联系实际,从三维坐标测量不确定度的目的、范围等方面对其进行分类分析。

关键词:三维坐标;测量;不确定度1目的提供完整的信息对三维坐标测量不确定度进行评定与表示,评价测量结果是否有效、是否可信,判定测量结果的质量。

2适用范围方法适用于Vento-R601620/2双悬臂地轨测量机的不确定度分析。

3三维坐标测量不确定度分析3.1A类标准不确定度分量表1是针对被测件长度(800mm)进行的10次等精度测量数据及计算平均值、残差、残差平方。

被测件长度10次测量的平均值x=799.99225 mm残差平方和=0.000178625mm2自由度n=n-1=9,n为测量次数。

据此可求出对应的估计的标准偏差:对于测量结果来说,我们通常把算术平均值的标准偏差称为A类标准不确定度。

而且由于被测量的A类标准不确定度uA按照正态分布,因此:3.2B类标准不确定度分量3.2.1测量仪器的不确定度UB1由于Vento-R601620/2三坐标测量机双臂测量的精度为:50+28L/1000≤108(μm),由此得出长度L≤2071.428571 mm。

当被测件的长度为800 mm时,由于其测量的半宽度U′遵循线性分布,因此U′可以由以下比例关系得出:其标准不确定度UB1为:UB1=U′/K=0.0417/1.7321=0.0241 mm 。

3.2.2由温度引起的测量不确定度UB2经反复测量比较,在环境温度为20℃附近,温度每增加或减少1度,测量结果就相应增加或减少0.01 mm,在20°±2℃相对恒温的正常测量条件下,由温度引起的测量半宽度为0.04 mm。

0.0231mm。

3.3 合成标准不确定度我们可以视合成标准不确定度分布为正态分布,将上述不确定度分量合成,得出合成标准不确定度Uc为:Uc=(UA2+UB12+UB22)1/2=0.03368mm3.4扩展不确定度我们也可以视扩展不确定度分布为正态分布,包含因子K=2.58,置信概率为99%,则扩展不确定度为:U=kUc=0.08689 mm被测件长度最终测量结果可表示为:L=799.99225±0.08689 mm4结语报告的长度是针对被测件长度做10次重复测量的平均值,且充分考虑了三坐标测量机双臂测量的精度对测量结果的影响,估计了由环境温度变化而引起的测量结果的差异,并在此基础上对测量结果作了相应的修正。

三坐标测量机测量不确定度评定摘要：三坐标测量机主要为工业设计、产品开发、加工制造以及质量检测等提供高精度的测量数据，但在应用时，我公司的三坐标测量机测量数据仅是被测参数接近真值的估测值，没有给出测量值的测量不确定度，不能高质量服务于高精尖产品的测量，本文主要对我公司三坐标测量机的不确定度进行评价。

三坐标测量机在测量中引起被测数值不确定度的因素有很多，不确定度可以分为随机不确定度和系统不确定度，在确定不确定度影响因素时，应从设备、人员、环境、方法及被测对象几个方面考虑。

关键词：不确定度、三坐标测量机、自由度概况本文参照规程JJF1059.1-2012《测量不确定度评定与表示》，使用海克斯康Micro Plus8106三坐标测量机，型号为GLOBAL PERFORMANCE8106，测量软件为QUINDOS7，设备规格为(800*1000*600)mm，本次重点研究三坐标测量机对标准环规直径测量的不确定度进行评定。

准确评定测量值与真值的误差，确定三坐标测量机的准确性和置信水准。

1、试验方案1.1试验条件试验环境温度为（202）C，温度变化每小时不应超过0.5℃/h，环境相对湿度为≤60%；将受测标准环规放置于实验室内的恒温时间为24小时以上，完全消除温度因素的影响。

1.2试验目的参照三坐标测量机操作规程及作业指导书，测量60mm3等标准环规的直径D，确定三坐标测量机的不确定度，对三坐标置信率进行评价。

1.3试验原理接触式，绝对测量。

1.4试验方法按设备操作要求按顺序开启软硬件，使三坐标测量机运行良好，参照三坐标测量机操作规程，选用三点法评价测量标准环规刻度线处的直径值D。

1.5注意事项试验前检查三坐标测量机及标准环规是否检定合格，试验开始时确保测头、标准环规无灰尘、油污的污染物，确保设备及被测件符合试验要求。

2、标准不确定度评定2.1由三坐标测量机本身测量误差引入的不确定度u1：6、实际应用与效果检查为某大学能源与动力工程学院参与的国家某重点项目提供气缸活塞配合间隙测量，通过对缸体与活塞的准确测量，借助本次研究成效对测量数据进行准确评定，提供高精度测量数据质量，为项目推进提供保障。

三坐标测量仪扫描法直径测量结果不确定度的评定摘要：三坐标测量仪精度高、应用范围广、能实现自动化测量，在精密尺寸测量中发挥巨大作用，但其在应用时，受到环境温度、测量方式等多种因素影响。

本文对蔡司标准球直径进行测量，分析三坐标测量仪测量结果中的误差来源，然后对测量数据进行较为科学的不确定度评定，提高测量结果的准确性和可靠性。

关键词：三坐标测量仪、扫描法、不确定度、直径测量三坐标测量仪作为精密尺寸测量设备，其测量精度高，结果准确，能实现自动化测量，大大提高测量效率[1,2]。

然而三坐标测量仪对测量结果要求较高，在进行精密测试时需考虑其测量数据是否准确。

测量过程中产生的误差不仅仅是由设备本身所带来的，通常还会受到测量环境温度、测量方式、被测对象等因素影响，导致测量值与真实值存在误差[3]。

杨胜华[4]提出三坐标测量仪误差来源于测量环境温度、震动、测量方式等准静态误差，仪器运动部件、导轨在测量时出现的动态误差；晁飞[5]提出除了环境温度外，还存在因为光栅材料的不均匀性，光栅系统操作困难等造成的光栅误差、零部件不匹配引起的装配误差。

测量不确定度表示由于测量误差的存在而对被测量值不能确定的程度，是评价测量结果质量的重要指标。

本文以蔡司公司提供的标准球为分析对象，使用三坐标测量仪对其进行直径测量，通过测量不确定度的评定对三坐标测量仪直径检测结果进行准确性和可靠性的评估[6]。

1 测量环境信息1.1 温湿度条件三坐标测量实验室内温度保持在18.0℃~22.0℃；湿度保持在40.0％~60％；压缩空气压力：0.5MPa。

1.2 设备信息仪器名称：三坐标测量仪规格型号：CONTURA 6206量程：X向0～900mm，Y向0～1200mm，Z向0～800mm长度测量最大允许误差MPE（E0.E150）≤1.8+L/350μm1.2 标准球信息Serial no. G-03786Material no.600332-8446-000Diameter 29.97418 mmMean radius 14.98709 mm1.3 测量方法将标准球固定在三坐标测量仪的大理石平面上，然后用三坐标测量仪扫描出球头形状，并在CAD模型中，将球头划分为4个90°的区域；测量程序设置为2个垂直的圆路径，以球形顶点为中点，测量角度为180°。

三坐标测量机校准装置建标技术要求及测量结果的不确定度评定文章摘要：随着经济建设的发展及外资企业的进入，三坐标测量机在许多三资企业、国有大中型企业及汽车零部件制造企业相继得到引进应用。

国内一些企业也生产各种不同精度、不同规格的三坐标测量机。

由于该种类型仪器的精度需要进行有效的实施监测，确保量值传递的准确性，才能使其在生产中发挥应有的作用，为此建立三坐标测量机校准装置是十分必要的。

关键词：三坐标测量机校准测量结果不确定度评定文章正文：三坐标测量机是现代精密加工中必不可少的精密测量设备，它不但可以完成常规二维坐标的测量，重要的是由于它的产生使得三维曲面的精确测量成为可能，特别是对复杂空间位置、空间曲面的测量不但可以成为可能，而且还可以通过CAD、CAM、CNC系统直接对加工机床进行加工过程的指导性控制。

由于它具有高精密度及由计算机系统控制的智能功能，因此被广泛应用于汽车、摩托车、航空航天、飞机制造及模具制造等加工业。

一、三坐标测量机校准装置计量标准的工作原理及其组成，根据JJF1064-2010《坐标测量机校准规范》，三坐标测量机示值误差校准方法和综合示值误差校准方法与原理如下：1、示值误差校准方法：按照JJF1064-2010的要求，采用激光干涉仪对三坐标测量机每一个坐标进行单独校准，并且要求在正、反行程方向进行校准。

原理如图1所示。

一、2、综合示值误差校准方法及原理：（1）单轴坐标综合示值误差的校准，将量块借助支撑架固定在平行于坐标轴线的任意位置，同时是处于工作行程的中间部位，原理如图2所示。

（2）空间综合示值误差的校准，将量块借助支撑架固定在三坐标测量机空间对角线方位的中间部位，这一检定分别在四个对角线进行，原理如如图3所示。

3、计量标准的组成：（1）激光干涉仪；（2）量块；（3）标准球。

二、三坐标测量机校准装置计量标准的主要技术指标1、激光干涉仪规格：XL-80测量范围：（0~80000）mmMPE：±（0.03+0.5L）μm2、量块（1）规格：30 mm、125mm、250mm、500mm、600mm、700mm、1000mm测量范围：（30~1000）mm等级：二等（2）规格：大八块测量范围：（125~500）mm等级：三等（3）规格：大五块测量范围：（600~1000）mm等级：三等3、标准球规格：Φ25mm、Φ19mm三、测量结果的不确定度评定1 概述1.1 测量方法：依据JJF1064-2010《坐标测量机校准规范》。

坐标测量机是一种集成了光电子、精密机械、计算机科学、测试计量技术与仪器仪表于一体的效率高、功能多的精密测试仪器，可以完成对很多工艺形貌复杂零件（工件）的快速、高效、准确测量。

与传统长度类尺寸测量仪器相比，三坐标测量机测量在自动化检测、测量精度控制、大型复杂工件测量方面拥有巨大的优越性。

三坐标测量机在广泛应用的同时，测量不确定度的准确合理评定方法也受到了关注。

只有测量参数结果中包含了测量不确定度的测量结果，测量参数结果才是精准的、可靠的、有应用价值的。

1　测量原理和模型三坐标测量机测量量块尺寸是通过建立空间坐标系测量量块端面“点-面”或者“面-面”距离而得到的，而被测坐标测量机测量范围视具体仪器而定。

一般单轴不超过1m ，其分辨率分为1μm 和0.1μm 两种。

测量精度在2μm 左右，尺寸测量误差用量块校准。

部分坐标测量机（如划线机）测量范围往往很大，最大可超过10m ，分辨率为1μm ，测量精度在10μm 量级，需要利用激光干涉仪对其单轴的测量精度进行补充校准。

其中，光栅尺是坐标测量机的基准，基准保持恒定才能确保结果可靠。

由于光栅尺本身几乎没有热膨胀，而且光栅尺在测量机中是悬浮安装，从而保证测量温度和测量精度。

在空间三维坐标系F (a ,b ,c )中，定义面V 和面V 1，面采点集合S i (i =1,2,…,N )为面V 上一组随机点。

依据点到平面的计算公式，令S i (i =1,2,…,N )为CMM 测头在标准器端面采集点，即端面的拟合平面为：Z =ax +by +c （1）则由最小二乘法的平面V 到平面V 1上S 点的距离为：221b a z c by ax l kk k ++−++=（2）在操作中应用测量原理时要注意以下几个方面：应用三坐标测量机几何量长度测量原理时，蓝宝石测头在测量前要进行校准测量，且探测误差测量值要在最大允许误差内，同时对于面上点集合的采集尽量使采集面的面积与量块实际面积的端面相当。

CMM尺寸测量不确定度模型与评定方法三坐标测量机(CMM)由于其测量任务的多样性和误差的复杂性,使得合理评定测量结果的不确定度非常困难,限制了测量机的应用,面向任务的不确定度评定已成为坐标测量机应用中亟待解决的难题。

论文以CMM尺寸测量为对象,针对CMM面向任务的不确定度分析、不确定度模型、不确定度估计方法等问题进行了较为系统深入的研究。

主要研究工作和创新点如下：(1)系统研究了测量不确定度分析方法。

指出通常的误差源分析方法不适合CMM面向任务的不确定度分析,提出了一种基于测量系统量值特性的不确定度分析法,该方法将测量系统统计分析与不确定度分析融为一体,使不确定度分析简单有效,且更具可操作性,适用于各种测量模型、测量方法和测量仪器,对测量不确定度的应用和推广具有重要意义。

(2)建立了CMM面向任务的不确定度模型。

给出了具体的不确定度透明箱和黑箱建模方法,提出了一种简单实用的虚拟坐标测量机评定方法(SVCMM)。

分析了基于测量模型的不确定度透明箱模型的适用性和局限性,重点研究了基于量值特性的不确定度黑箱模型在CMM面向任务不确定度评定中的应用。

(3)系统研究不确定度估计方法,比较了灵敏度分析方法、蒙特卡罗方法(MCM)及SVCMM三种方法的适用性,提出了采用量值特性不确定度分析法、不确定度黑箱模型、MCM随机仿真与统计参数估计的优化组合,进行CMM面向任务的测量不确定度评定,对科学合理评定测量不确定度发挥重要作用。

(4)基于上述不确定度理论与方法,研究了CMM三种典型尺寸测量方案的不确定度评定,根据各种测量方案的不确定度评定结果,分析讨论了测量方案与测量精度的关系,为提升CMM的应用价值提供可靠的理论依据。

(5)编制了CMM面向尺寸测量任务的测量不确定度离线评定软件,对测量不确定度进行自动评定,并给出符合产品几何技术规范(GPS)的测量结果报告,为实现CMM测量不确定度的智能化评定奠定了基础。

(6)通过评定实例,讨论了不同评定方法的一致性和差异性,总结了不同评定方法的特点及适用性,验证了采用量值分析建立不确定度黑箱模型,并结合MCM 应用于测量结果评定,是解决CMM面向任务的测量不确定度评定的最优方案,为提升CMM应用价值提供参考。