二轮复习11空间几何体训练题
- 格式:doc
- 大小:171.00 KB
- 文档页数:11

空间几何体练习题一、填空题1. 设矩形长为6 cm,宽为4 cm,高为3 cm,则矩形的体积为__________。
2. 已知一个圆柱的底面积为28π cm²,高为10 cm,则该圆柱的体积为__________。
3. 一个正方体的体积为125 cm³,则它的边长为__________。
4. 底面积为48 cm²的直角三角形棱柱,高为10 cm,则该棱柱的体积为__________。
5. 一个圆锥的底面积为36π cm²,高为8 cm,则该圆锥的体积为__________。
二、选择题1. 已知一个长方体的长、宽、高分别为a cm、b cm、c cm,则该长方体的体积为()。
A. abc cm³B. ab+bc+ca cm³C. 2(ab+bc+ca) cm³D. a²b²c² cm³2. 一个边长为2 cm的正方体,把它的每条边拉长为原来的2倍,则这个正方体的体积是原来的()。
A. 2 倍B. 4 倍C. 6 倍D. 8 倍3. 已知一个正方锥的底面积为16 cm²,高为12 cm,则该正方锥的体积为()。
A. 64 cm³B. 128 cm³C. 192 cm³D. 256 cm³4. 一个长方体,它的底面是一个边长为6 cm的正方形,高为8 cm,底面积是原来的()。
A. 1/3B. 2/3C. 3/4D. 4/35. 设一个棱长为a cm的正方体的体积为V cm³,把每条边的长度都加倍后得到一个新的正方体,则这个新的正方体的体积为()。
A. V cm³B. 2V cm³C. 4V cm³D. 8V cm³三、解答题1. 某圆锥的底面积为12π cm²,高为9 cm,试求该圆锥的体积,并保留最简整数。
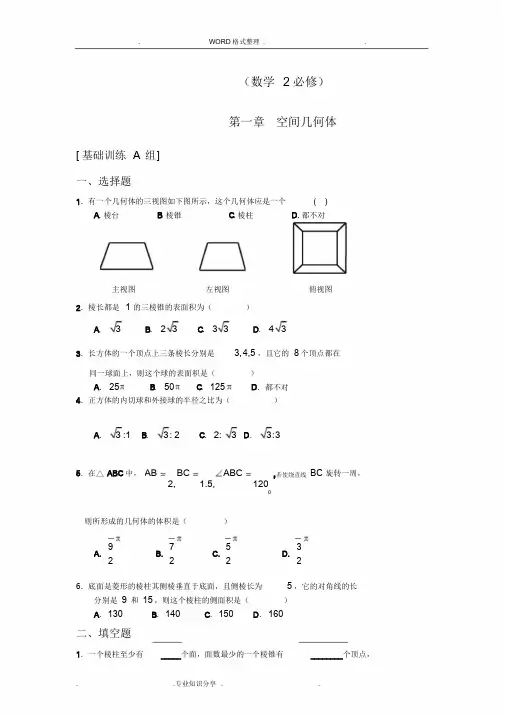
(数学 2 必修)第一章空间几何体[ 基础训练A组]一、选择题1.有一个几何体的三视图如下图所示,这个几何体应是一个( )A. 棱台B. 棱锥C. 棱柱D. 都不对主视图左视图俯视图2.棱长都是1的三棱锥的表面积为()A. 3B. 2 3C. 3 3D. 4 33.长方体的一个顶点上三条棱长分别是3, 4,5 ,且它的8 个顶点都在同一球面上,则这个球的表面积是()A.25 B.50 C.125 D.都不对4.正方体的内切球和外接球的半径之比为()A. 3 :1 B.3: 2 C.2: 3 D.3:35.在△ABC中,AB BC ABC ,若使绕直线BC 旋转一周,2, 1.5, 120则所形成的几何体的体积是()A. 92B.72C.52D.326.底面是菱形的棱柱其侧棱垂直于底面,且侧棱长为 5 ,它的对角线的长分别是9和15 ,则这个棱柱的侧面积是()A.130 B.140 C.150 D.160二、填空题1.一个棱柱至少有_____个面,面数最少的一个棱锥有________个顶点,. .专业知识分享. .顶点最少的一个棱台有________条侧棱。
2.若三个球的表面积之比是1: 2 :3,则它们的体积之比是_____________。
3.正方体ABCD A1B1C1D1 中,O是上底面ABCD 中心,若正方体的棱长为a,则三棱锥O AB D 的体积为_____________。
1 14.如图,E,F 分别为正方体的面ADD1 A1 、面BCC1B1 的中心,则四边形B F D1E 在该正方体的面上的射影可能是____________ 。
5.已知一个长方体共一顶点的三个面的面积分别是 2 、 3 、 6 ,这个长方体的对角线长是___________;若长方体的共顶点的三个侧面面积分别为3,5,15 ,则它的体积为___________.三、解答题1.养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12M ,高4M ,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大4M (高不变);二是高度增加4M (底面直径不变)。

专题五 立体几何第1讲 空间几何体1.圆x 2+(y +1)2=3绕直线kx -y -1=0旋转一周所得的几何体的体积为( )A .36πB .12πC .43πD .4π2.若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积等于( ) A. 3 B .2C .2 3D .63.(2010年唐山一中质检)已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是( )A .16πB .20πC .24πD .32π4.一个平面四边形的斜二测画法的直观图是一个边长为a 的正方形,则原平面四边形的面积等于( )A.24a 2 B .22a 2 C.22a 2 D.2a 2 5.已知一个圆锥的底面半径为R ,高为H ,在圆锥内有一个内接圆柱,当圆柱的侧面积为12πRH 时,圆柱的母线长为( ) A.H 5 B.H 4C.H 3D.H 26.(2010年河南开封调研)四面体的六条棱中,有五条棱长都等于a ,则该四面体的体积的最大值为( )A.38a 3B.28a 3 C.18a 3 D.112a 3 7.下面是关于四棱柱的四个命题:①若有两个侧面垂直于底面,则该四棱柱为直四棱柱;②若两个过相对侧棱的截面都垂直于底面,则该四棱柱为直四棱柱;③若四个侧面两两全等,则该四棱柱为直四棱柱;④若四棱柱的四条对角线两两相等,则该四棱柱为直四棱柱.其中真命题的编号是______(写出所有真命题的编号).8.如图所示两组立体图形都是由相同的小正方体拼成的.(1)图(1)的正(主)视图与图(2)的________相同.(2)图(3)的________图与图(4)的________图不同.9.(2010年高考天津卷)一个几何体的三视图如图所示,则这个几何体的体积为____________.10.如图,一个倒圆锥形容器,它的轴截面是正三角形,在容器内放一个半径为r的铁球,并向容器内注水,使水面恰与铁球相切,将球取出后,容器内的水深是多少?11.(2010年高考陕西卷)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB,BP=BC=2,E,F分别是PB,PC的中点.(1)证明:EF∥平面P AD;(2)求三棱锥E-ABC的体积V.12.一个空间几何体的三视图及部分数据如图所示.(1)请画出该几何体的直观图,并求它的体积;(2)证明:A1C⊥平面AB1C1;(3)若D是棱CC1的中点,在棱AB上取中点E.判断DE是否平行于平面AB1C1?并证明你的结论.第3讲 空间向量与立体几何1.在正三棱柱ABC -A 1B 1C 1中,D 是CC 1的中点,F 是A 1B 的中点,且DF →=αAB →+βAC →,则( )A.α=12,β=-1 B .α=-12,β=1 C .α=1,β=-12 D .α=-1,β=122.(2010年山东曲阜市调研)已知平面α内有一个点M (1,-1,2),它的一个法向量为n =(6,-3,6),则下列点P 中,在平面α内的是( )A .P (2,3,3)B .P (-2,0,1)C .P (-4,4,0)D .P (3,-3,4)3.如图所示,在正方体ABCD -A 1B 1C 1D 1中,棱长为a ,M 、N 分别为A 1B 和AC 上的点,A 1M =AN =2a 3,则MN 与平面BB 1C 1C 的位置关系是( ) A .相交 B .平行C .垂直D .不能确定4.(2009年高考江西卷)如图,正四面体ABCD 的顶点A ,B ,C 分别在两两垂直的三条射线Ox ,Oy ,Oz 上,则在下列命题中,错误的为( )A .O -ABC 是正三棱锥B .直线OB ∥平面ACDC .直线AD 与OB 所成的角是45°D .二面角D -OB -A 为45°5.已知长方体ABCD -A 1B 1C 1D 1中,AB =BC =1,AA 1=2,E 是侧棱BB 1的中点,则直线AE 与平面A 1ED 1所成角的大小为( )A .60°B .90°C .45°D .以上都不正确6.已知正方体ABCD -A 1B 1C 1D 1的棱长为1,点P 在线段BD 1上,当∠APC 最大时,三棱锥P -ABC 的体积为( )A.124B.118C.19D.1127.已知向量a =(0,-1,1),b =(4,1,0),|λa +b |=29且λ>0,则λ=________.8.在一直角坐标系中已知A (-1,6),B (3,-8),现沿x 轴将坐标平面折成60°的二面角,则折叠后A 、B 两点间的距离为________.9.将正方形ABCD 沿对角线BD 折成直二面角A —BD —C ,有如下四个结论:①AC ⊥BD ;②△ACD是等边三角形;③AB与平面BCD所成的角为60°;④AB与CD所成的角为60°.其中正确的序号是________.(写出你认为正确的结论的序号)10.(2010年高考湖南卷)如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M是棱CC1的中点.(1)求异面直线A1M和C1D1所成的角的正切值;(2)证明:平面ABM⊥平面A1B1M.11.如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E、F分别是AB、PB的中点.(1)求证:EF⊥CD;(2)求DB与平面DEF所成角的正弦值.12.如图,在直三棱柱ABC-A1B1C1中,已知BC=1,BB1=2,AB⊥平面BB1C1C.(1)求直线C1B与底面ABC所成角的正切值;(2)在棱CC1(不包括端点C、C1)上确定一点E的位置,使EA⊥EB1(要求说明理由);(3)在(2)的条件下,若AB=2,求二面角A-EB1-A1的大小.专题五第1讲 空间几何体1.【解析】选C.直线kx -y -1=0过圆x 2+(y +1)2=3的圆心(0,-1),故所得几何体是半径为3的球,其体积为43π(3)3=43π,故选C. 2.【解析】选D.由正视图还原实物图知,该几何体的高是1,底面边长是2的正三棱柱,S 侧=2×1×3=6.3.【解析】选C.设正四棱柱的底面边长为a ,球半径为R ,则⎩⎨⎧(2R )2=16+(2a )2a 2·4=16,解得a =2,R 2=6, ∴球的表面积S =4πR 2=24π.4.【解析】选B.根据斜二测画法画平面图形直观图的规则,可以得出原图的面积S 与它的直观图的面积S ′之间的关系是S ′=24S ,又因为直观图的面积为a 2,所以原平面四边形的面积等于a 224=22a 2. 5.【解析】选D.设圆柱的母线长为x ,底面半径为r ,由r R =H -x H ,得r =R -R H·x , 那么圆柱的侧面积S =2πrx =2πx (R -R H ·x )=-2πR H ·x 2+2πRx , 则-2πR H ·x 2+2πRx =12πRH ⇒(2x -H )2=0⇒x =H 2.故所求圆柱的母线长为H 2. 6.【解析】选C.法一:设三棱锥另一棱长BC =x ,如图所示,取BC 的中点E ,连结AE 、DE ,易证BC 垂直于平面ADE ,故V A -BCD =13S △ADE ·BE +13S △ADE ·EC =13S △ADE ·BC =13·12·a ·3a 2-x 22x =a 12x 2(3a 2-x 2)≤a 12·x 2+(3a 2-x 2)2=a 38, 当且仅当x 2=(3a 2-x 2)⇒x =62a 时取得等号. 法二:如图,底ABD 是固定的,当C 运动时,显然当平面CAD ⊥平面ABD 时高最大,体积最大, V max =13·(34a 2)·32a =a 38.7.【解析】①错,必须是两个相邻的侧面.②正确.③错,反例,可以是一个斜四棱锥.④正确,对角钱两两相等,则此两条对角线组成的平行四边形为矩形,故正确答案为②④.【答案】②④8.【解析】对于第一组的两个立体图形,图(1)的正(主)视图与图(2)的俯视图相同.对于第二组的两个立体图形,图(3)的正(主)视图与图(4)的正(主)视图不同,而侧(左)视图和俯视图都是相同的.【答案】(1)俯视图 (2)正视 正视9.【解析】该几何体是上面是底面边长为2的正四棱锥,下面是底面边长为1、高为2的正四棱柱的组合体,其体积为V =1×1×2+13×22×1=103. 【答案】10310.【解】如图,由题意知,轴截面P AB 为正三角形,故当球在容器内时,水深为3r ,水面半径为3r ,容器内水的体积是V =V 圆锥-V 球=π3(3r )2·3r -43πr 3=53πr 3. 将球取出后,设容器中水的深度为h ,则水面半径为33h . 此时容器内水的体积为V ′=π3(33h )2·h =π9h 3. 由V ′=V ,得h =315 r .即铁球取出后水深为315 r .11.【解】(1)证明:在△PBC 中,E ,F 分别是PB ,PC 的中点,∴EF ∥BC .∵四边形ABCD 为矩形,∴BC ∥AD ,∴EF ∥AD .∵AD ⊂平面P AD ,EF ⊄平面P AD ,∴EF ∥平面P AD .(2)连结AE ,AC ,EC ,过E 作EG ∥P A 交AB 于点G ,则EG ⊥平面ABCD ,且EG =12P A . 在△P AB 中,AP =AB ,∠P AB =90°,BP =2,∴AP =AB =2,EG =22. ∴S △ABC =12AB ·BC =12×2×2=2, ∴V E -ABC =13S △ABC ·EG =13×2×22=13. 12.【解】(1)几何体的直观图如图.第 - 10 - 页 版权所有@中国高考志愿填报门BB 1C 1C 是矩形,BB 1=CC 1=3,BC =1,AA 1C 1C 是边长为3的正方形,且垂直于底面BB 1C 1C .∴其体积V =12×1×3×3=32. (2)证明:∵∠ACB =90°,∴BC ⊥AC.∵三棱柱ABC —A 1B 1C 1为直三棱柱,∴BC ⊥CC 1.∵AC ∩CC 1=C ,∴BC ⊥平面ACC 1A 1,∴BC ⊥A 1C .∵B 1C 1∥BC ,∴B 1C 1⊥A 1C .∵四边形ACC 1A 1为正方形,∴A 1C ⊥AC 1.∵B 1C 1∩AC 1=C 1∴A 1C ⊥平面AB 1C 1.(3)当E 为棱AB 的中点时,DE ∥平面AB 1C 1.证明:如图,取BB 1的中点F ,连结EF ,FD ,DE ,∵D ,E ,F 分别为CC 1,AB ,BB 1的中点,∴EF ∥AB 1.∵AB 1⊂平面AB 1C 1,EF ⊄平面AB 1C 1,∴EF ∥平面AB 1C 1.∵FD ∥B 1C 1,∴FD ∥面AB 1C 1,又EF ∩FD =F ,∴面DEF ∥面AB 1C 1.而DE ⊂面DEF ,∴DE ∥面AB 1C 1.。

(数学2必修) 第一章 空间几何体[基础训练A 组] 一、选择题1.有一个几何体的三视图如下图所示,这个几何体应是一个( )A.棱台B.棱锥C.棱柱D.都不对2.棱长都是1的三棱锥的表面积为( )A. 3B. 23C. 33D. 433.长方体的一个顶点上三条棱长分别是3,4,5,且它的8个顶点都在 同一球面上,则这个球的表面积是( )A .25πB .50πC .125πD .都不对 4.正方体的内切球和外接球的半径之比为( )A .3:1B .3:2C .2:3D .3:35.在△ABC 中,02, 1.5,120AB BC ABC ==∠=,若使绕直线BC 旋转一周,则所形成的几何体的体积是( )A.92π B. 72π C. 52π D. 32π 6.底面是菱形的棱柱其侧棱垂直于底面,且侧棱长为5,它的对角线的长 分别是9和15,则这个棱柱的侧面积是( ) A .130 B .140 C .150 D .160二、填空题1.一个棱柱至少有 _____个面,面数最少的一个棱锥有 ________个顶点,主视图 左视图 俯视图顶点最少的一个棱台有 ________条侧棱。
2.若三个球的表面积之比是1:2:3,则它们的体积之比是_____________。
3.正方体1111ABCD A B C D - 中,O 是上底面ABCD 中心,若正方体的棱长为a ,则三棱锥11O AB D -的体积为_____________。
4.如图,,E F 分别为正方体的面11A ADD 、面11B BCC 的中心,则四边形E BFD 1在该正方体的面上的射影可能是____________。
5.已知一个长方体共一顶点的三个面的面积分别是2、3、6,这个长方体的对角线长是___________;若长方体的共顶点的三个侧面面积分别为3,5,15,则它的体积为___________.三、解答题1.养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12M ,高4M ,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大4M (高不变);二是高度增加4M (底面直径不变)。
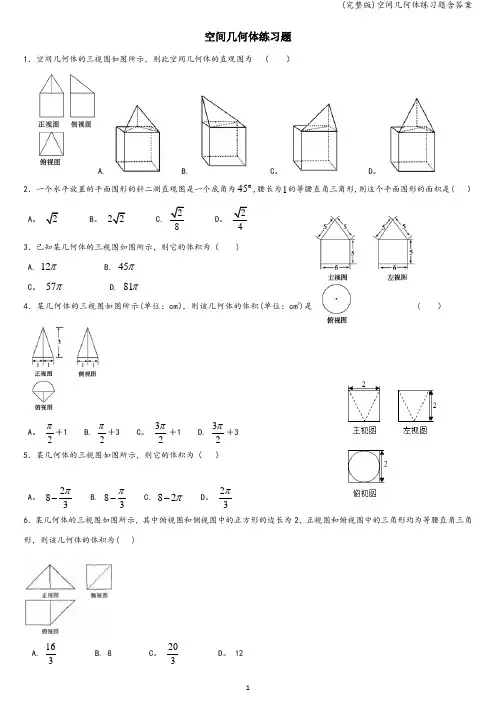
空间几何体练习题1.空间几何体的三视图如图所示,则此空间几何体的直观图为 ( )A. B. C 。
D 。
2.一个水平放置的平面图形的斜二测直观图是一个底角为45︒,腰长为1的等腰直角三角形,则这个平面图形的面积是( ) A 。
2 B 。
22 C. 28 D 。
243.已知某几何体的三视图如图所示,则它的体积为( )A. 12πB. 45πC 。
57π D. 81π4.某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:cm 3)是 ( )A 。
2π+1 B. 2π+3 C 。
32π+1 D. 32π+3 5.某几何体的三视图如图所示,则它的体积为( )A 。
283π- B. 83π- C. 82π- D 。
23π6.某几何体的三视图如图所示,其中俯视图和侧视图中的正方形的边长为2,正视图和俯视图中的三角形均为等腰直角三角形,则该几何体的体积为( )A. 163B. 8 C 。
203D 。
127.某空间几何体的三视图如图所示,则该几何体的体积为()A. 16+2πB. 16+π C。
8+π D。
8+2π8.某空间几何体的三视图如图所示,则该几何体的体积为( )A。
4 B. 6 C。
8 D。
169.将棱长为2的正方体削成一个体积最大的球,则这个球的体积为()A. 163π B.43πC.323π D。
4π10.如图是三棱锥D ABC-的三视图,则该三棱锥的外接球体积为( )A。
92πB。
33πC. 62πD.23π11.某空间几何体的正视图是三角形,则该几何体不可能是()A。
圆锥 B。
圆柱 C. 四面体 D. 三棱锥12.若一个正三棱柱的三视图如下图所示,则这个正三棱柱的高和底面边长分别为( ).A. 2, 22 B。
2,4 C. 23,2 D。
4,313.某几何体的三视图如图所示,则该几何体的表面积是( )A.3222++B。
53222++ C.3322++D。

A空间几何体部分1、如果一个水平放置的图形的斜二测直观图是一个底面为45o,腰和上底均为1的等腰梯形,那么原平面图形的面积是( )A. 2+1+2、半径为R 的半圆卷成一个圆锥,则它的体积为() 3R 3R 3R 3R 3、一个棱柱是正四棱柱的条件是A 、底面是正方形,有两个侧面是矩形B 、底面是正方形,有两个侧面垂直于底面C 、底面是菱形,且有一个顶点处的三条棱两两垂直D 、每个侧面都是全等矩形的四棱柱4.有一个几何体的三视图如下图所示,这个几何体应是一个A 、棱台B 、棱锥C 、棱柱D 、都不对5.在棱长为1的正方体上,分别用过共顶点的三条棱中点的平面截该正方形,则截去8个三棱锥后 ,剩下的几何体的体积是( )A.23 B. 76 C. 45D. 566.长方体的一个顶点上三条棱长分别是3、4、5,且它的8个顶点都在同一球面上,则这个球的表面积是A 、25πB 、50πC 、125πD 、都不对 7.正方体的内切球和外接球的半径之比为()A.B.2 C. 2 D.38.在△ABC 中,AB=2,BC=1.5,∠A BC=120o,若使绕直线BC 旋转一周,则所形成的几何体的体积是A. 92π B. 72π C. 52π D. 32π9、圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为84π,则圆台较小底面的半径为A 、7B 、6C 、5D 、3 10.直三棱柱ABC —A 1B 1C 1的体积为V ,点P 、Q 分别在 侧棱AA 1和CC 1上,AP=C 1Q ,则四棱锥B —APQC 的体积为A 、2VB 、3VC 、4VD 、5V 11、如图,在多面体ABCDEF 中,已知平面ABCD 是边长为3的正 方形,EF ∥AB,32EF =,且EF 与平面ABCD 的距离为2,则该多面体的体积为( )正视图侧视图俯视图_ A _BBB 1DCC 1AEE 1D 1A 1FF 1A 、92 、5 C 、6 D 、15212、如右图所示,正三棱锥V-ABC中,D,E,F分别是VC ,VA,AC 的中点,P为VB上任意一点,则直线DE与PF 所成的角的大小是( )A6π B 2π C 3πD 随P点的变化而变化。

空间几何体测试题、选择题(本大题共 12题,每小题5分,共60 分)1•小明在上海世博会参观时, 看到一个几何体,它的轴截面一定是圆面,则这个几何体是 () A .圆柱B .圆锥C .球D .圆台2•一个正三棱锥和一个正四棱锥,它们的棱长都相等,把这个正三棱锥的一个侧面重合在正 四棱锥的一个侧面上,这个组合体可能是 () A .正五棱锥 B .斜三棱柱C .正三棱柱D .直三棱柱 3•四棱锥的四个侧面中,直角三角形最多可能有( )A . 1个B . 2个C . 3个D . 4个4•下列5个命题中:①三角形的直观图是三角形;②平行四边形的直观图是平行四边形 ;③正方形的直观图是正方形, ④如果一个三角形的平行投影仍是三角形 ,那么它的中位线的平行投影一定是这个三角形的平行投影的对应的中位线; ⑤棱台各侧棱的延长线交于一点,正确的说法有() A. 1个 B. 2个C. 3个D. 4个5•长方体的三个面的面积分别是 2, 3, 6 , 则长方体的对角线长是()A .6 B . 3 C . 2.3 D . 3 . 26•若正四棱锥S-ABCD 的三视图中,正视图、侧视图都是腰为 3,底边为2的等腰三角形,俯视图是边长为 2的正方形,则正四棱锥 S-ABCD 的侧面积为( )A.2,3B. 4 3C. 1D.27•半径为R 的半圆卷成一个圆锥,则它的体积为()积分别为V 1和V 2,则圆柱除圆锥外的体积与圆锥的体积之比为( )的最短矩离是A . 5B . 7C . 29D . 3711.图3为图2所示几何体的展开图,则拼成一个棱长为6 cm 的正方体如图4,需要这样的几何体()A.仝R 324B.R 3 248 •如图1,一个空间几何体的主视图(正视图) 、侧视图是周长为16的一 个内角为60°的菱形,俯视图是圆及其圆心,那么这个几何体的表面积为 ()A.8B.12C.16D.209.一个圆锥放在一个底面积相等、 高也相等的圆柱内,若圆锥与圆柱的体 A ・2:3 B ・ 2:1 C ・ 1:3 D ・ 3:110 .小蚂蚁的家住在长方体ABCD — A 1B 1C 1D 1的A 处,小蚂蚁的奶奶家住在C 1处,三条棱长分别是 AA 1=1, AB=2 , AD=4,小蚂蚁从A 点出发,沿长方体的表面到小蚂蚁奶奶家 C 1A. 2个B. 3个C. 4个D. 5个图2 图3 图412. 一个四棱锥和一个三棱锥恰好可以拼接成一个三棱柱.这个四棱锥的底面为正方形,且 底面边长与各侧棱长相等, 这个三棱锥的底面边长与各侧棱长也都相等. 设四棱锥、三棱锥、三棱柱的高分别为h i , h 2, h 3,则h i : h 2 : h 3等于()A . .3:1:1B . ,3:2:2C . .3:2: .2 二、填空题(本大题共 4小题,每小题5分,共20分) 13. 一个直径为32厘米的圆柱形水桶中放入一个铁球, 球全部没入水中后,水面升高9厘米,则此球的半径为 __________ .14. 若三棱锥V ABC 侧棱相等,底面是正三角形,三棱锥V ABC 的正视图、俯视图如图 5所示,其中VA 4,AC 2 3 ,/---------- 1-------------- ifivn则该三棱锥的侧视图的面积为 ___________ .15. 一个正四棱柱的各个顶点在一个直径为 2cm 的球面上.如果正四棱柱的底面边长为 1cm ,那么该棱柱的表面积为 ________ cm 2 . 16•如图6, —个广告气球被一束入射角为 45°的平行光线照射,其投影是个最长的弦长为5米的椭圆,则这个广告气球直径是 _____________ 米.三、解答题(本大题共 6小题,共70分)17. (10分)用斜二测画法作出边长为 3cm 、高4cm 的矩形的直观图. 18. (12分)正方体 ABCD-A 1B 1C 1D 1的边长为a. (1)求三棱锥A-A 1BD 的表面积和体积.⑵ 求三棱锥B-A 1C 1D 的体积.19. (12分)将圆心角为120°,面积为3的扇形作为圆锥的侧面,求圆锥的表面积和体积 20. (12分)已知正三棱锥 S-ABC 的高SO=h,斜高SM=n,求经过SO 的中点且平行于底面的 截面△ A 1B 1C 1的面积.21. (12分)棱长均为a 的三棱锥容器内装水,若顶点向下倒立时,水面高在容器高的中点处. (1) 求水的体积和棱锥的体积比 .(2) 若棱锥顶点向上正立时,水面高是容器高的几分之几?22. (12分)养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用) ,已建的仓库的底面直径为 12 m ,高4 m ,养路处拟建一个更大的圆锥形仓库,以存放更多食盐, 现有两种方案:一是新建的仓库的底面直径比原来增加4m (高不变);二是高度增加4m (底D ..3:2:.3面直径不变)(1 )分别计算按这两种方案所建的仓库的体积;(2) 分别计算按这两种方案所建的仓库的表面积; (3) 哪个方案更经济些?空间几何体章末测试题一、选择题1~6 CBDDAB 7~12 AC BABB 提示:2.重合时不会构成正五棱锥,只能是三棱柱3•在正方体 ABCD — A i B i C i D i 中的四棱锥 D — A 1B 1C 1D 1的四个面都是直角三角形,故选 D.4. 其中正确的命题为①②④⑤,故选D.5. 设长方体的边长分别为 a 、b 、c ,则有ab= 2, ac= , bc= V 6,a=1,b= V 2,c= 3, 对角线l 2=a 2+b 2+c 2=6,故对角线的长为 「6.16.正四棱锥的侧面是底边为 2,高为.3的等腰三角形,故侧面积是 4x - x2x . 3=4 3 ,2 故选B.1J 37.设圆锥底面半径为r ,则有2 r R 得r -R ,故圆锥的高为R ,所以圆锥的体积2 2为:V 1 (1R)2^3 R -^R 3,故选 A.3 2 2 248.由题意知,该几何体是两个连体的圆锥,底面半径是2,母线长是4,故表面积是两个圆锥的侧面积之和为 22 4 16 ,故选C.9. 设底面面积为S,高为h ,则V 1:V 2 1:3,故圆锥外圆柱的体积与圆锥的体积之比为 2:1 ,选B.10. 根据题意知:蚂蚁所走的路线有三种情况(如图①②③) ,有勾股定理可得 :图①中AC 1= 32 42 5,图②中AC 1 =.62 12 37, 图③中 AC 1= 52 22 .29, 故选A.11. 需3个.它们是 D 1-ABCD, D 1-BB 1C 1C , D 1-A 1ABB 1,故选 B.6—12.由题意知三棱锥为正四面体,设三棱锥棱长为a,则 h 2— a ,同理可求出四棱锥的体3V四棱锥二3 T a T a 自,又由一V三棱锥-迥2 亞3则有 一? a 3 —3 a 2 h 3,解得 h 3= 6 a ,所以 h | : h 2 : h 3 = 3:2:2,故选 B. 4 4 3 二、填空题 —513.12cm 14. 615.2 4 216•—「22提示:13.由题意知,球的体积等于排出水的体积,即 162 9 - R 3,解得R 12厘米.3为底边,三棱锥的高为高的三角形,由题意知三棱锥的高是 2 3,所以侧视图的面积是 6.作D ' C '平行X '的直线,且等于 B '所得四边形A ' B ' C ' D⑵体积为a 3 4 ^a6所以 S= R 2+3=4 ,高 h - 32 12 2 2 ,14•由正视图知道侧棱长是 4,俯视图知底面边长是2 3,侧视图看到的是以三棱锥底边BC15•如图,正四棱柱 ABCD A 1BQ 1D 1的对角线 BD 1为外接球的直径,可求得棱柱的高 DD 1 .2 ,故 S 2( AB BC AB AA 1 AD AA 1)2 4、 2.三、解答题17.解:(1)在已知ABCD 画对应X '轴,中取AB 、AD 所在边为 Y '轴使/ X ' O ' Y ' =45 X 轴与Y 轴,相交于0点(O O与A 重合),轴上取 A B '使 A ' B ' =AB ,在 Y '轴上取 D ',使 A '1 =_ AD ,2A 'B '的长.就是矩形ABCD 的直观图.18•解:(1)表面积为a 23-,体积为]爲2 2 3 219.解:由圆心角为1200,面积为3的扇形,得—l 23 ,即 I =3.3又扇形弧长等于圆锥底面周长,即故 R=1,C' X'故体积为V=1 R 2h “2—3 320.解:设底面正三角形的边长为 a ,在RT A SOM 中, SO=h SM=n所以 OM=n 212,又 MO ^a,即 a=.j 2,所以 s ABC —a 23、. 3(n 2 l 2),截面面积为 \ 3(n 2 l 2).4411 21.解:(1)设底面面积是S ,咼为h ,则水面面积是S ,咼为 h ,故体积之比为421 1 1S h 3 4 22S 6 6 10 96 m 2,(3) 方案2更好,因为体积增大的多,表面积增加的少方案2:直径为 12m ,高为1 8m ,此时体积变为V- 以父28836 8 m 3,233 (1)方案1 :直径变为 16m ,高为4m ,母线长为l . 484-、5,此时表面积为S 828 4、5 (64 32、5) m 2,125622.解:("方案1:直径变为16m ,高为4m ,此时体积为V1 382 4-V m3,方案2 :直径为12m ,高为8m ,母线长为|故水的体积和棱锥的体积比为 1:8.(2)设空气的体积为 V ,底面为S ,高为h ,椎体的体积为 V,底面为S ,高为h ,由V -,V 821sh 1斗 即 3 3 hL1 1」Sh 1Sh 3 3(h)3h1,得丄辽,故鱼8 h 2 H 全2 37 2 82 62 10,此时表面积为。

专题11 空间几何体1.以选择、填空题形式考查空间位置关系的判断,及文字语言、图形语言、符号语言的转换,难度适中;2.以熟悉的几何体为背景,考查多面体或旋转体的侧面积、表面积和体积计算,间接考查空间位置关系的判断及转化思想等,常以三视图形式给出几何体,辅以考查识图、用图能力及空间想象能力,难度中等.3.几何体的三视图与表(侧)面积、体积计算结合;1.柱体、锥体、台体、球的结构特征2.柱体、锥体、台体、球的表面积与体积3.空间几何体的三视图和直观图(1)空间几何体的三视图三视图的正视图、侧视图、俯视图分别是从物体的正前方、正左方、正上方看到的物体轮廓线的正投影围成的平面图形,三视图的画法规则为“长对正、高平齐、宽相等”.(2)空间几何体的直观图空间几何体直观图的画法常采用斜二测画法.用斜二测画法画平面图形的直观图规则为“轴夹角45°(或135°),平行长不变,垂直长减半”.4.几何体沿表面某两点的最短距离问题一般用展开图解决;不规则几何体求体积一般用割补法和等积法求解;三视图问题要特别留意各种视图与观察者的相对位置关系.【误区警示】1.识读三视图时,要特别注意观察者的方位与三视图的对应关系和虚实线.2.注意复合体的表面积计算,特别是一个几何体切割去一部分后剩余部分的表面积计算.要弄清增加和减少的部分.3.展开与折叠、卷起问题中,要注意平面图形与直观图中几何量的对应关系.高频考点一三视图、直观图例1.(2018年北京卷)某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为A. 1B. 2C. 3D. 4【变式探究】【2017课标1】某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形,这些梯形的面积之和为A.10B.12C.14D.16【变式探究】下图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为( )(A)20π(B)24π(C)28π(D)32π【变式探究】某三棱锥的三视图如图所示,则该三棱锥的表面积是( )A .2+ 5B .4+ 5C .2+2 5D .5 高频考点二 几何体的表面积例2.(2019·高考全国卷Ⅲ)学生到工厂劳动实践,利用3D 打印技术制作模型.如图,该模型为长方体ABCD -A 1B 1C 1D 1挖去四棱锥O -EFGH 后所得的几何体,其中O 为长方体的中心,E ,F ,G ,H 分别为所在棱的中点,AB =BC =6 cm ,AA 1=4 cm.3D 打印所用原料密度为0.9 g/cm 3.不考虑打印损耗,制作该模型所需原料的质量为________g.【举一反三】(2018·高考全国卷Ⅲ)已知圆锥的顶点为S ,母线SA ,SB 所成角的余弦值为78,SA 与圆锥底面所成角为45°.若△SAB 的面积为515,则该圆锥的侧面积为________.【变式探究】(1)已知某几何体是一个平面将一正方体截去一部分后所得,该几何体的三视图如图所示,则该几何体的表面积为( )A .20+23B .18+23C .18+ 3D .20+3(2)已知某几何体的三视图如图,则该几何体的表面积是( )A .39π4+3 3 B .45π4+33C .23π2D .49π4【变式探究】一个几何体的三视图如图所示,则该几何体的表面积为( )A .3πB .4πC .2π+4D .3π+4 高频考点三 几何体的体积例3.(2018年江苏卷)如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为________.【变式探究】某几何体的三视图如图所示,则该几何体的体积为( )A.13+π B .23+π C.13+2π D.23+2π【变式探究】已知一所有棱长都是2的三棱锥,则该三棱锥的体积为________. 高频考点四 与球有关的切、接问题例4.(2019·高考全国卷Ⅲ )已知三棱锥P ABC 的四个顶点在球O 的球面上,P A =PB =PC ,△ABC 是边长为2的正三角形,E ,F 分别是P A ,AB 的中点,∠CEF =90°,则球O 的体积为( )A .86πB .46πC .26πD .6π【举一反三】(2018·高考全国卷Ⅲ)设A ,B ,C ,D 是同一个半径为4的球的球面上四点,△ABC 为等边三角形且其面积为93,则三棱锥D ABC 体积的最大值为( )A .12 3B .183C .24 3D .54 3【变式探究】(2017·高考全国卷Ⅲ)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )A .πB .3π4C .π2D .π4【变式探究】如图,在四棱锥P ABCD 中,底面ABCD 为菱形,PB ⊥底面ABCD ,O 为对角线AC 与BD 的交点,若PB =1,∠APB =∠BAD =π3,则三棱锥P AOB 的外接球的体积是________.【举一反三】在四棱锥P ABCD 中,四边形ABCD 是边长为2a 的正方形,PD ⊥底面ABCD ,且PD =2a ,若在这个四棱锥内放一个球,则该球半径的最大值为________.1.【2019年高考全国Ⅲ卷理数】已知三棱锥P −ABC 的四个顶点在球O 的球面上,P A =PB =PC ,△ABC 是边长为2的正三角形,E ,F 分别是P A ,AB 的中点,∠CEF =90°,则球O 的体积为A .B .C .D2.【2019年高考浙江卷】祖暅是我国南北朝时代的伟大科学家,他提出的“幂势既同,则积不容异”称为祖暅原理,利用该原理可以得到柱体的体积公式V 柱体=Sh ,其中S 是柱体的底面积,h 是柱体的高.若某柱体的三视图如图所示(单位:cm),则该柱体的体积(单位:cm 3)是A .158B .162C .182D .3243.【2019年高考全国Ⅲ卷理数】学生到工厂劳动实践,利用3D 打印技术制作模型.如图,该模型为长方体1111ABCD A B C D -挖去四棱锥O —EFGH 后所得的几何体,其中O 为长方体的中心,E ,F ,G ,H 分别为所在棱的中点,16cm 4cm AB =BC =, AA =,3D 打印所用原料密度为0.9 g/cm 3,不考虑打印损耗,制作该模型所需原料的质量为___________g.4.【2019年高考北京卷理数】某几何体是由一个正方体去掉一个四棱柱所得,其三视图如图所示.如果网格纸上小正方形的边长为1,那么该几何体的体积为__________.5.【2019年高考天津卷理数】已知四棱锥的底面是边长为2的正方形,侧棱长均为5.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的体积为_____________.6.【2019年高考江苏卷】如图,长方体1111ABCD A B C D 的体积是120,E 为1CC 的中点,则三棱锥E −BCD 的体积是 ▲ .1. (2018年北京卷)某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为A. 1B. 2C. 3D. 42. (2018年全国Ⅲ卷)中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是A. AB. BC. CD. D3. (2018年浙江卷)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是A. 2B. 4C. 6D. 84. (2018年浙江卷)已知四棱锥S−ABCD的底面是正方形,侧棱长均相等,E是线段AB上的点(不含端点),设SE与BC所成的角为θ1,SE与平面ABCD所成的角为θ2,二面角S−AB−C的平面角为θ3,则A. θ1≤θ2≤θ3B. θ3≤θ2≤θ1C. θ1≤θ3≤θ2D. θ2≤θ3≤θ15. (2018年全国I卷)已知正方体的棱长为1,每条棱所在直线与平面α所成的角都相等,则α截此正方体所得截面面积的最大值为A. B. C. D.6. (2018年全国I卷)某圆柱的高为2,底面周长为16,其三视图如右图.圆柱表面上的点在正视6. (2018年全国I卷)某圆柱的高为2,底面周长为16,其三视图如右图.圆柱表面上的点在正视图上的对应点为,圆柱表面上的点在左视图上的对应点为,则在此圆柱侧面上,从到的路径中,最短路径的长度为A. B.C. D. 27. (2018年全国Ⅲ卷)设是同一个半径为4的球的球面上四点,为等边三角形且其面积为,则三棱锥体积的最大值为A. B. C. D.8. (2018年全国Ⅲ卷)在长方体中,,,则异面直线与所成角的余弦值为A. B. C. D.9. (2018年天津卷) 已知正方体的棱长为1,除面外,该正方体其余各面的中心分别为点E,F,G,H,M(如图),则四棱锥的体积为__________.10. (2018年江苏卷)如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为________.11. (2018年全国Ⅲ卷) 已知圆锥的顶点为,母线,所成角的余弦值为,与圆锥底面所成角为45°,若的面积为,则该圆锥的侧面积为__________.1.【2017课标1,理7】某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形,这些梯形的面积之和为A.10B.12C.14D.162.【2017课标II,理4】如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为( )A.90πB.63πC.42πD.36π3.【2017北京,理7】某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为232(D)24.【2017山东,理13】由一个长方体和两个14圆柱体构成的几何体的三视图如右图,则该几何体的体积为.5.【2017课标1,理16】如图,圆形纸片的圆心为O,半径为5 cm,该纸片上的等边三角形ABC的中心为O.D、E、F为圆O上的点,△DBC,△ECA,△F AB分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△F AB,使得D、E、F重合,得到三棱锥.当△ABC 的边长变化时,所得三棱锥体积(单位:cm3)的最大值为_______.1、【2016高考新课标1卷】如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是283π,则它的表面积是( )(A)17π(B)18π(C)20π(D)28π2.【2016高考新课标2】下图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为( )(A)20π(B)24π(C)28π(D)32π3.【2016年高考北京】某三棱锥的三视图如图所示,则该三棱锥的体积为()A.16B.13C.12D.14.【2016高考新课标3】如图,网格纸上小正方形的边长为1,粗实现画出的是某多面体的三视图,则该多面体的表面积为( )(A)18365+(B)54185+(C)90 (D)815.【2016高考山东】一个由半球和四棱锥组成的几何体,其三视图如图所示.则该几何体的体积为( )(A)1233+π(B)1233+π(C)1236+π(D)216+π1.列一元一次方程解应用题的一般步骤(1)审题:弄清题意.(2)找出等量关系:找出能够表示本题含义的相等关系.(3)设出未知数,列出方程:设出未知数后,表示出有关的含字母的式子,•然后利用已找出的等量关系列出方程.(4)解方程:解所列的方程,求出未知数的值.(5)检验,写答案:检验所求出的未知数的值是否是方程的解,•是否符合实际,检验后写出答案.2.和差倍分问题:增长量=原有量×增长率现在量=原有量+增长量3.等积变形问题:常见几何图形的面积、体积、周长计算公式,依据形虽变,但体积不变.①圆柱体的体积公式 V=底面积×高=S·h= r2h②长方体的体积 V=长×宽×高=abc4.数字问题一般可设个位数字为a,十位数字为b,百位数字为c.十位数可表示为10b+a,百位数可表示为100c+10b+a.然后抓住数字间或新数、原数之间的关系找等量关系列方程.5.市场经济问题(1)商品利润=商品售价-商品成本价(2)商品利润率=商品利润×100%商品成本价(3)商品销售额=商品销售价×商品销售量(4)商品的销售利润=(销售价-成本价)×销售量(5)商品打几折出售,就是按原标价的百分之几十出售,如商品打8折出售,即按原标价的80%出售.6.行程问题:路程=速度×时间时间=路程÷速度速度=路程÷时间(1)相遇问题:快行距+慢行距=原距(2)追及问题:快行距-慢行距=原距(3)航行问题:顺水(风)速度=静水(风)速度+水流(风)速度逆水(风)速度=静水(风)速度-水流(风)速度抓住两码头间距离不变,水流速和船速(静不速)不变的特点考虑相等关系.7.工程问题:工作量=工作效率×工作时间完成某项任务的各工作量的和=总工作量=18.储蓄问题利润=每个期数内的利息×100% 利息=本金×利率×期数本金实际问题与二元一次方程组题型归纳(练习题答案)类型一:列二元一次方程组解决——行程问题【变式1】甲、乙两人相距36千米,相向而行,如果甲比乙先走2小时,那么他们在乙出发2.5小时后相遇;如果乙比甲先走2小时,那么他们在甲出发3小时后相遇,甲、乙两人每小时各走多少千米?解:设甲,乙速度分别为x,y千米/时,依题意得:(2.5+2)x+2.5y=363x+(3+2)y=36解得:x=6,y=3.6答:甲的速度是6千米/每小时,乙的速度是3.6千米/每小时。

专题升级训练11 空间几何体的三视图、表面积及体积 (时间:60分钟 满分:100分)一、选择题(本大题共8小题,每小题5分,共40分) 1.下列四个几何体中,每个几何体的三视图中有且仅有两个视图相同的是( ). A.①② B.①③ C.③④ D.②④ 2.用斜二测画法画一个水平放置的平面图形的直观图为如图所示的一个正方形,则原来的图形是( ). 3.在一个几何体的三视图中,正(主)视图和俯视图如图所示,则相应的侧(左)视图可以为( ). 4.(2012·北京丰台区三月模拟,5)若正四棱锥的正(主)视图和俯视图如图所示,则该几何体的表面积是( ). A.4B.4+4 C.8D.4+4 5.(2012·浙江宁波十校联考,12)已知某几何体的三视图如图所示,其中侧(左)视图是等腰直角三角形,正视图是直角三角形,俯视图ABCD是直角梯形,则此几何体的体积为( ). A.1 B.2 C.3 D.4 6.(2012·山东济南三月模拟,8)若一个螺栓的底面是正六边形,它的正(主)视图和俯视图如图所示,则它的体积是( ). A.27+12πB.9+12π C.27+3πD.54+3π 7.(2012·浙江宁波模拟,13)已知一个正三棱锥的正(主)视图为等腰直角三角形,其尺寸如图所示,则其侧(左)视图的周长为( ). A.5+ B.5+6 C.6+6 D.3+12 8.长方体的三条棱长分别为1,,,则此长方体外接球的体积与面积之比为( ). A. B.1 C.2 D. 二、填空题(本大题共4小题,每小题4分,共16分) 9.(2012·浙江宁波十校联考,15)已知两个圆锥有公共底面,且两圆锥的顶点和底面圆周都在半径为3的同一个球面上.若两圆锥的高的比为1∶2,则两圆锥的体积之和为__________. 10.(2012·江苏南京二模,11)一块边长为10 cm的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形作侧面,以它们的公共顶点P为顶点,加工成一个如图所示的正四棱锥容器,当x=6 cm时,该容器的容积为__________cm3. 11.如图,直三棱柱ABC-A1B1C1中,AB=1,BC=2,AC=,AA1=3,M为线段BB1上的一动点,则当AM+MC1最小时,△AMC1的面积为__________. 12.(2012·浙江湖州中学模拟,16)底面边长为1,侧棱长为2的正四棱柱ABCD-A1B1C1D1的8个顶点都在球O的表面上,E是侧棱AA1的中点,F是正方形ABCD的中心,则直线EF被球O所截得的线段长为__________. 三、解答题(本大题共4小题,共44分.解答应写出必要的文字说明、证明过程或演算步骤) 13.(本小题满分10分)如图,已知某几何体的三视图如下(单位:cm). (1)画出这个几何体的直观图(不要求写画法); (2)求这个几何体的表面积及体积. 14.(本小题满分10分)斜三棱柱ABC-A1B1C1的底面是边长为a的正三角形,侧棱长等于b,一条侧棱AA1与底面相邻两边AB,AC都成45°角. (1)求这个三棱柱的侧面积; (2)求这个三棱柱的体积. 15.(本小题满分12分)(2012·安徽安庆二模,18)如图,几何体ABC-EFD是由直三棱柱截得的,EF∥AB,∠ABC=90°,AC=2AB=2,CD=2AE=. (1)求三棱锥D-BCE的体积; (2)求证:CE⊥DB. 16.(本小题满分12分)(2012·河北邯郸一模,19)已知四棱锥E-ABCD的底面为菱形,且∠ABC=60°,AB=EC=2,AE=BE=,O为AB的中点. (1)求证:EO⊥平面ABCD; (2)求点D到平面AEC的距离. 一、选择题 1.D 解析:图①的三种视图均相同;图②的正(主)视图与侧(左)视图相同;图③的三种视图均不相同;图④的正(主)视图与侧(左)视图相同. 2.A 解析:由直观图可知,在直观图中多边形为正方形,对角线长为,所以原图形为平行四边形,位于y轴上的对角线长为2,故选A. 3.D 解析:由题目所给的几何体的正(主)视图和俯视图,可知该几何体为半圆锥和三棱锥的组合体,如图所示: 可知侧(左)视图为等腰三角形,且轮廓线为实线,故选D. 4.B 5.D 解析:由三视图可得该几何体是四棱锥,记为棱锥PABCD,且PD⊥底面ABCD. 从而此几何体的体积为××2×2=4. 6.C 解析:该螺栓是由一个正六棱柱和一个圆柱组合而成的, V总=V正六棱柱+V圆柱=×32×6×2+π×12×3=27+3π. 7.A 解析:由正(主)视图可知正三棱锥的底边长为6,高为3,从而可得侧棱长为.而侧(左)视图是一个三角形,三条边分别是底面正三角形的高、侧棱和侧面等腰三角形底边上的高,其长度依次为3,和2,故侧(左)视图的周长为5+. 8.D 二、填空题 9.16π 解析:设两圆锥的高分别为h,2h,圆锥的底面圆半径为r,则r2=2h2. 又球的半径R==3,则h=2. 故两圆锥的体积之和为V=πr2(2h+h)=πr2h=2πh3=16π. 10.48 11. 解析:将直三棱柱沿侧棱A1A剪开,得平面图形如图所示,A′C1为定长,当A,M,C1共线时AM+MC1最短,此时AM=,MC1=2. 又在原图形中AC1=,易知∠AMC1=120°, ∴=××2×sin 120°=. 12. 解析:O,E,F三点在平面ACC1A1内,且矩形ACC1A1的外接圆是球的一个大圆. 又EF∥A1C,设A到直线A1C的距离为d,则=,得d=,故圆心O到直线EF的距离为. 又球的半径为,故直线EF被球O所截得的线段长为2=. 三、解答题 13.解:(1)这个几何体的直观图如图所示. (2)这个几何体可看成是正方体AC1及直三棱柱B1C1Q-A1D1P的组合体. 由PA1=PD1=,A1D1=AD=2,可得PA1⊥PD1. 故所求几何体的表面积S=5×22+2×2×+2××()2=22+4(cm2). 所求几何体的体积V=23+×()2×2=10(cm3). 14.解:(1)由题可知AA1⊥BC,S侧=SBCC1B1+2SABB1A1=(1+)ab. (2)设O为A1在平面ABC内的射影,则由题可知O在∠BAC的平分线上,可得AO=(b·cos 45°)÷cos 30°=b,则斜三棱柱的高A1O=b,所以三棱柱的体积V=·=. 15.(1)解:BC2=AC2-AB2=3BC=. 几何体ABC-EFD是由直三棱柱截得,由图可知DC⊥平面ABC, ∴DC⊥AB. 又∵∠ABC=90°,∴AB⊥BC.∴AB⊥平面BDC. 又EF∥AB,∴EF⊥平面BCD. 故VD-BCE=VE-BCD=S△BCD·EF=××××1=. CF. 依题意?EF⊥BD.① 又在Rt△BCF和Rt△CDB中, ==,=== Rt△BCF∽Rt△CDB?∠BDC=∠BCF∠BDC+∠DCF=∠BCF+∠DCF=90°CF⊥BD.② 由①②BD⊥平面CEF. 又CE平面CEF,∴BD⊥CE. 16.(1)证明:连接CO. ∵AE=EB=,AB=2,∴△AEB为等腰直角三角形. ∵O为AB的中点,∴EO⊥AB,EO=1. 又∵四边形ABCD是菱形,∠ABC=60°, ∴△ACB是等边三角形,∴CO=. 又EC=2,∴EC2=EO2+CO2,∴EO⊥CO. 又CO平面ABCD,EO平面ABCD,∴EO⊥平面ABCD. (2)解:设点D到平面AEC的距离为h. ∵AE=,AC=EC=2,∴S△AEC=. ∵S△ADC=,E到平面ACB的距离EO=1,VD-AEC=VE-ADC, ∴S△AEC·h=S△ADC·EO,∴h=, ∴点D到平面AEC的距离为.。

卜人入州八九几市潮王学校专题限时集训(十一)[第11讲空间几何体](时间是:45分钟)1.将长方体截去一个四棱锥后,得到的几何体的直观图如图11-1所示,那么该几何体的俯视图为()图11-1图11-22.一个多面体的三视图如图11-3所示,其中正视图是正方形,侧视图是等腰三角形.那么该几何体的外表积为()图11-3A.88B.98 C.108D.1583.一个简单组合体的三视图及尺寸如图11-4所示(单位:mm),那么该组合体的体积为()图11-4A.32 mm3B.48 mm3C.56 mm3D.64 mm34.一个简单几何体的正视图、侧视图如图11-5所示,那么其俯视图不可能为....①长方形;②正方形;③圆;④椭圆.其中正确的选项是()图11-5A.①②B.②③C.③④D.①④5.体积为的正三棱柱(底面是正三角形且侧棱垂直底面)的三视图如图11-6所示,那么此三棱柱的高为()图11-6A.B.C.1D.6.如图11-7所示是一个几何体的三视图,那么该几何体的体积为()图11-7A.1B.C.D.7.空间几何体的三视图如图11-8所示,那么该几何体的各侧面图形中,是直角三角形的有()图11-8A.0个B.1个C.2个D.3个8.有一个棱长为1的正方体,按任意方向正投影,其投影面积的最大值是()A.1B.C.D.9.某个几何体的三视图如图11-9,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是()图11-9A.cm3B.cm3C.cm3D.cm310.一个物体的底座是两个一样的几何体,它的三视图及其尺寸(单位:dm)如图11-10所示,那么这个物体的体积为()图11-10A.(120+16π)dm3B.(120+8π)dm3C.(120+4π)dm3D.(60+8π)dm311.某型号冰淇淋上半局部是半球,下半局部是圆锥,其正视图如图11-11所示,那么该型号冰淇淋的体积等于________.图11-1112.一个几何体的三视图如图11-12所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,该几何体的体积是________;假设该几何体的所有顶点在同一球面上,那么球的外表积是________.图11-1213.如图11-13,三棱锥O-ABC,OA,OB,OC两两垂直且长度均为6,长为2的线段MN的一个端点M 在棱OA上运动,另一个端点N在△OBC内运动(含边界),那么MN的中点P的轨迹与三棱锥的面OAB,OBC,OAC围成的几何体的体积为________.图11-13专题限时集训(十一)【根底演练】1.C[解析]长方体的侧面与底面垂直,所以俯视图是C.2.A[解析]由三视图可知,该几何体是一个横放的三棱柱,底面三角形是等腰三角形(底为6,高为4),三棱柱的高为4,故底面三角形的腰长为S=×6×4×2A.3.D[解析]两个柱体的组合.体积是6×4×1+2×4×5=64.4.B[解析]由于正视图和侧视图的底边长度不同,故俯视图一定不是正方形和圆.【提升训练】5.C[解析]正三棱柱的底面三角形高为,故边长为2,设正三棱柱的高为h,那么由正三棱柱的体积公式有,=×2××h⇒h=1.6.B[解析]由题意可知,该几何体为一个四棱锥,底面面积为,高为1,体积为V=××1=.应选B.7.C[解析]这个空间几何体直观图如图,其中侧面PAD⊥底面ABCD,侧面中只有△PAB,△PCD为直角三角形,另外两个是非直角的等腰三角形.8.D[解析]如下列图是棱长为1的正方体,当投影线与平面A1BC1垂直时,因为平面ACD1∥平面A1BC1,所以此时正方体的正投影为一个正六边形,设其边长为a,那么a=,所以a=,所以投影面的面积为6××=,此时投影面积最大.应选D.9.C[解析]这个几何体为三棱锥P-ABC,如下列图.由三视图可知,平面PAC⊥平面ABC,所以V P-ABC=hS△ABC=×2××2×2=cm3.应选C.10.B[解析]该物体的上半局部是一个长方体,其长,宽,高分别为15,4,2,体积为15×2×4=120dm3.下局部是两个半圆柱,合并起来是一个圆柱,其底面半径为2,高也是2,故其体积为π×22×2=8πdm3.故这个物体的体积为(120+8π)dm3.11.54π[解析]冰淇淋上半局部是半球,下半局部是圆锥,V=π×33+π×32×12=54π.12.3π[解析]该空间几何体是底面边长和高均为1且一条侧棱垂直底面的四棱锥,其体积为×12×1=;这个四棱锥与单位正方体具有一样的外接球,故外接球的半径为,所以其外表积为4π×=3π.13.[解析]根据三角形MON是以O为直角顶点的直角三角形,故OP==1,即点P的轨迹是以点O为球心的八分之一球面,其与三棱锥的三个侧面围成的空间几何体的体积为×=.。

考点33 空间几何体的结构及其三视图和直观图、空间几何体的表面积与体积一、选择题1.(2012·江西高考文科·T7)若一个几何体的三视图如图所示,则此几何体的体积为()A.112B.5 C.4 D. 92【解题指南】由三视图想像出几何体的直观图,由直观图求得体积。
【解析】选D.由三视图可判断该几何体为直六棱柱,其底面积为4,高为1,所以体积为4.2.(2012·新课标全国高考文科·T7)与(2012·新课标全国高考理科·T7)相同如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为()A.6 B.9 C.12 D.18【解题指南】由三视图想像出几何体的直观图,由直观图求得体积。
【解析】选B.由题意知,此几何体是三棱锥,其高h=3,相应底面面积为111=63=9,==93=9233S V Sh ⨯⨯∴⨯⨯.3.(2012·新课标全国高考理科·T11)已知三棱锥S-ABC 的所有顶点都在球O 的球面上,△ABC 是边长为1的正三角形,SC 为球O 的直径,且SC=2,则此棱锥的体积为( )A B. C. D.【解题指南】思路一:取AB 的中点为D 将棱锥分割为两部分,利用B CDS A CDS V V V --=+求体积;思路二:设点O 到面ABC 的距离为d,利用123ABC V S d ∆=⨯求体积;思路三:利用排除法求解.【解析】选A 方法一:SC 是球O 的直径,90CAS CBS ∴∠=∠=︒1BA BC AC ===,2SC =,AS BS ∴==,取AB 的中点为D ,显然AB CD ⊥,AB CS ⊥,AB ∴⊥平面CDS在CDS ∆中,CD ,DS =,2SC =,利用余弦定理可得cosCDS ∠=故sin CDS ∠=12CDS S ∆∴==13B CDS A CDS CDS V V V S BD --∆∴=+=⨯⨯+1111333CDS CDS S AD S BA ∆∆⨯=⨯==方法二:ABC ∆的外接圆的半径r =,点O 到面ABC 的距离d ==SC 为球O 的直径⇒点S 到面ABC 的距离为2d =此棱锥的体积为11233ABC V S d ∆=⨯==.方法三:123ABC V S R ∆<⨯=排除,,B C D . 4.(2012·新课标全国高考文科·T8)平面α截球O 的球面所得圆的半径为1,球心O 到平面α的距离为2,则此球的体积为( )(A )6π (B )43π (C )46π (D )63π【解题指南】利用球心到截面的距离、截面圆的半径、球的半径之间满足勾股关系求得球的半径,然后利用公式求得球的体积。
适考素能特训
(对应学生用书P133)
一、选择题
1.(改编题)已知三棱锥的俯视图与侧视图如图所示,俯视图是边长为2的正三角形,侧视图是有一直角边为2的直角三角形,则该三棱锥的正视图可能为()
[解析]由于空间几何体的正视图和侧视图“高平齐”,故正视图的高一定是2,由于正视图和俯视图“长对正”,故正视图的底面边长为2,又根据侧视图可知这个空间几何体最前面的面垂直于底面,这个面遮住了后面的一个侧棱,综上可知,这个空间几何体的正视图可能是C.
[答案] C
2.(2012·郑州质检2)一个几何体的三视图及其尺寸如图所示(单位:cm),其中正(主)视图是直角三角形,侧(左)视图是半圆,俯视图是等腰三角形,则这个几何体的体积是()
A.π
2 cm
3 B.π
3 cm 3 C.π
4 cm 3
D. π cm 3
[解析] 依题意得,该几何体是一个圆锥的一半(沿圆锥的轴剖开),其中该圆锥的底面半径为1、高为3,因此该几何体的体积为12×(1
3×π×12×3)=π
2 cm 3,选A.
[答案] A
3.(2012·云南名校联考)一个体积为123的正三棱柱的三视图如图所示,则这个三棱柱的侧(左)视图的面积为 ( )
A.12B.8C.83D.6 3
[解析]根据三视图中“宽相等”知,底面正三角形(即俯视图)
的高为23,∴底面边长为4,∴V=
3
4×4
2·h=123(其中h为三棱
柱的高),∴h=3,又∵侧视图的矩形的宽即为几何体的高,∴S侧视图=23×3=6 3.
[答案] D
4.(2012·哈师大附中)一个几何体的三视图如图所示,则侧视图的面积为()
A .2+3
B .1+ 3
C .2+23
D .4+ 3
[解析] 依题意得,该几何体的侧视图的面积等于22
+1
2×2 ×3=4+ 3.
[答案] D
5. (2012·
重庆,文9)设四面体的六条棱的长分别为1,1,1,1,2和a ,且长为a 的棱与长为2的棱异面,则a 的取值范围是( )
A. (0,2)
B. (0,3)
C. (1,2)
D. (1,3)
[解析] 四面体如图1所示.
设AB =AC =BD =CD =1,AD =2,BC =a ,则a >0,当A ,B ,C ,D 四点共面时,BC =2(如图2所示).
而此时A ,B ,C ,D 不能构成四面体,所以BC <2,故选A.
[答案] A 二、填空题
6.已知一个几何体的三视图如图所示,则该几何体的体积为________.
[解析] 结合三视图可知,该几何体是由底面边长为2、高为2的正三棱柱除去上面的一个高为1的三棱锥后得到的,其直观图如图所示,故该几何体的体积为12×2×2sin60°×2-13×12×2×2sin60°×1
=533.
[答案]
533
7.圆柱形容器内部盛有高度为8 cm 的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是________ cm.
[解析] 设球的半径为r cm ,则πr 2
×8+43πr 3
×3=πr 2×6r .解得r
=4.
[答案] 4
8. (2012·江苏,7)如图,在长方体ABCD -A 1B 1C 1D 1中,AB =AD =3 cm ,AA 1=2 cm ,则四棱锥A -BB 1D 1D 的体积为________cm 3.
[解析] 由已知可得,V A -BB 1D 1D =23V A 1D 1B 1-ADB =23×1
2V A 1B 1C 1D 1-ABCD
=23×1
2×3×3×2=6(cm 3).
[答案] 6
9.(2012·乌鲁木齐二诊)球O 与底面边长为3的正三棱柱的各侧面均相切,则球O 的表面积为________.
[解析] 依题意得,设球O 的半径为R ,底面正三角形内切圆半径就是球O 的半径,则R =13×332=32,因此球O 的表面积S =4πR 2=3π.
[答案] 3π 三、解答题
10. (2012·陕西,文18)直三棱柱ABC -A 1B 1C 1中,AB =AA 1,∠CAB =π2.
(1)证明:CB 1⊥BA 1;
(2)已知AB =2,BC =5,求三棱锥C 1-ABA 1的体积. [解] (1)证明:如图,连接AB 1,
∵ABC -A 1B 1C 1是直三棱柱,∠CAB =π
2, ∴AC ⊥平面ABB 1A 1.故AC ⊥BA 1.
又∵AB =AA 1,∴四边形ABB 1A 1是正方形. ∴BA 1⊥AB 1.又CA ∩AB 1=A , ∴BA 1⊥平面CAB 1.故CB 1⊥BA 1.
(2)∵AB =AA 1=2,BC =5,∴AC =A 1C 1=1. 由(1)知,A 1C 1⊥平面ABA 1, ∴V C 1-ABA 1=13S △ABA 1·A 1C 1=13×2×1=2
3
. 11.(2012·江门市一模)如图,已知四棱柱ABCD -A 1B 1C 1D 1的俯视图是边长为3的正方形,侧视图是长为3宽为3的矩形.
(1)求该四棱柱的体积;
(2)取DD1的中点E,证明:面BCE⊥面ADD1A1.
[解](1)四棱柱的底面是矩形,侧面ABB1A1与底面ABCD垂直,过A1作底面垂线的垂足是AB的中点,四棱柱的体积V=S矩ABCD×h
=AB×AD×h=2×3×3=6 3.
(2)证明:连接CD1,依题意△CDD1是正三角形,所以CE⊥DD1.
又AD⊥面CDD1C1,CE⊂面CDD1C1,所以AD⊥CE.
因为AD∩DD1=D,所以CE⊥面ADD1A1.
因为CE⊂面BCE,所以面BCE⊥面ADD1A1.
12.(2012·西安中学一模)
如图,FD垂直于矩形ABCD所在平面,CE∥DF,∠DEF=90°.
(1)求证:BE∥平面ADF;
(2)若矩形ABCD的一个边AB=3,EF=23,则另一边BC的长为何值时,三棱锥F-BDE的体积为3?
[解](1)证明:过点E作CD的平行线交DF于点M,连接AM.
因为CE∥DF,所以四边形CEMD是平行四边形,可得
EM=CD且EM∥CD,于是四边形BEMA也是平行四边形,所
以有BE∥AM,而直线BE在平面ADF外,所以BE∥平面ADF.
(2)由EF=23,EM=AB=3,得FM=3且∠MFE=30°. 由∠DEF=90°可得FD=4,从而得DE=2.
因为BC⊥CD,BC⊥FD,所以BC⊥平面CDFE.
所以,V F-BDE=V B-DEF=1
3S△DEF×BC.
因为S△DEF=1
2DE×EF=23,V F-BDE=3,所以BC=
3
2.
综上,当BC=3
2时,三棱锥F-BDE的体积为 3.。