用混合罚函数法求解气举区块优化配气模型
- 格式:pdf
- 大小:447.96 KB
- 文档页数:8
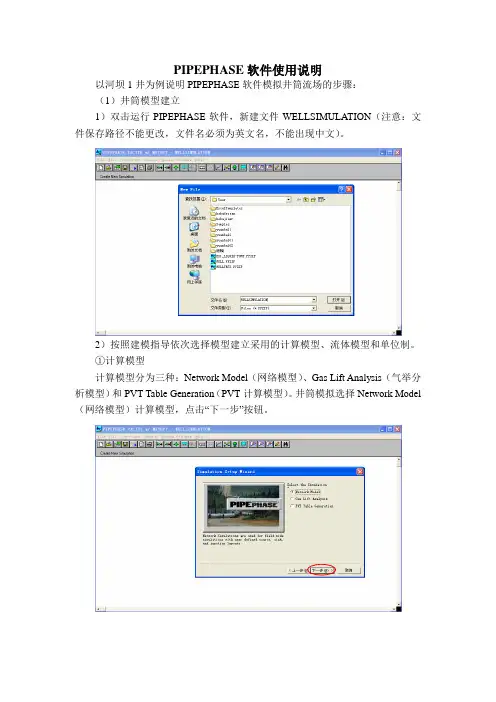
PIPEPHASE软件使用说明以河坝1井为例说明PIPEPHASE软件模拟井筒流场的步骤:(1)井筒模型建立1)双击运行PIPEPHASE软件,新建文件WELLSIMULATION(注意:文件保存路径不能更改,文件名必须为英文名,不能出现中文)。
2)按照建模指导依次选择模型建立采用的计算模型、流体模型和单位制。
①计算模型计算模型分为三种:Network Model(网络模型)、Gas Lift Analysis(气举分析模型)和PVT Table Generation(PVT计算模型)。
井筒模拟选择Network Model (网络模型)计算模型,点击“下一步”按钮。
②流体模型流体模型分为七种:Blackoil(黑油模型)、Compositional(组分模型)、P Compositional/ Blackoil(混合模型)、Gas Condensate(凝析气模型)、Liquid(液体模型)、Gas(气体模型)和Steam(蒸汽模型)。
井筒模拟选择Compositional (组分模型),点击“下一步”按钮。
组分模型计算选择Rigorous Multi-Phase(严格多相流),点击“下一步”按钮。
③单位制单位制分为五种:English(英制单位)、Petroleum(石油单位)、Metric(公制单位)、SI(国际单位)和Custom Settings(用户自定义单位)。
本文选择SI (国际单位),点击“下一步”按钮。
3)添加组分。
①点击Library Components(组分库)下面的Add(添加)按钮。
②依次选中需要添加的组分,点击Add Compents(添加组分)按钮,然后在点击OK按钮。
③再次点击OK按钮,添加组分完成。
4)建立模型。
①点击快捷栏中的Add Source to Flowsheet(添加源节点)按钮,在工作区域建立源节点S001;点击快捷栏中的Add Sink to Flowsheet(添加汇节点)按钮,在工作区域建立汇节点D002。

基于AMESim和遗传算法的发动机配气相位仿真与优化张文铎;王自勤;田丰果;陈家兑【摘要】为了验证一种新型全可变配气系统的工作效果和为下一步发动机台架试验提供数据参考,基于AMEsim软件建立了单缸自然吸气汽油发动机模型,并以函数模块形式在发动机模型中嵌入上述新型全可变配气系统.结合上述全可变配气系统的调节特性,使用遗传算法对全可变配气系统的配气调节参数进行优化,分别以最大充量系数和最小泵气损失为优化目标,得到满负荷不同转速下的最佳进气晚关角和排气早开角.经过优化,发动机充量系数和扭矩均有一定程度提高.【期刊名称】《机械设计与制造》【年(卷),期】2016(000)007【总页数】5页(P20-23,28)【关键词】全可变配气系统;发动机;AMESim;遗产算法;优化;配气相位【作者】张文铎;王自勤;田丰果;陈家兑【作者单位】贵州大学现代制造技术教育部重点实验室,贵州贵阳550000;贵州大学现代制造技术教育部重点实验室,贵州贵阳550000;贵州大学现代制造技术教育部重点实验室,贵州贵阳550000;贵州大学现代制造技术教育部重点实验室,贵州贵阳550000【正文语种】中文【中图分类】TH16;TK417发动机可变配气技术是通过改变发动机进、排气门开启和关闭时刻以及气门升程,以满足发动机不同转速和负荷工况下对进、排气流通特性的要求,从而有效地提高充气效率,改善发动机的燃油经济性、动力性和排放[1-4]。
目前,国外实现大规模商用的技术方案有丰田的VVT-i,本田的i-VETC,宝马的Valvetronic等,这些技术方案主要是基于机械式的,只能实现改变凸轮轴转角或者凸轮形线的阶段式突变或者配气相位和升程的有限连续可变[2-3]。
而国内对此项技术研究起步相对较晚,国产汽车厂商主要以仿制国外技术为主,缺少拥有自主知识产权的可变配气技术。
贵州大学发动机可变配气技术课题组提出了一种基于机械与液压装置的新型全可变配气系统,可对气门相位角和气门升程的进行独立、连续调节,能满足发动机各个转速和负荷工况下的最佳配气策略需求。

中国科技信息2015年第01期·CHINA SCIENCE AND TECHNOLOGY INFORMATION Jan.2015-114-信息技术推广概述在工程设计中管道工艺模拟计算软件有很多,如PIPESIM、PIPESYS、OLGA、PIPEFLOW、PIPEPHASE、TACET 等,在混输管道计算中,PIPESIM、OLGA 和PIPESYS 是比较常用的三种软件,三种软件均可以用来进行模拟计算,并互相验证。
根据管道运行工况选择合适的软件和恰当的关联式,以保证计算的精确度。
软件介绍PIPESIM 软件PIPESIM 软件是斯伦贝谢公司开发的、针对油藏、井筒和地面管网等设施模拟计算的设计软件。
其基础模块功能包括:单井设计分析和人工举升、管道设计和管径优化、设备计算选型等。
PIPESIM 对流体的描述分为黑油模型和组分模型。
黑油模型可以对油、气、水三相、气液两相以及单相液体进行模拟计算;组分模型可以对化学组份不同的碳氢化合物进行模拟计算。
OLGA 软件OLGA 软件是由挪威著名的SPT 石油技术公司开发研制。
可以模拟在油井、输油管线和油气处理设备中的油、气、水的运动状态。
该软件已经被广泛应用于可行性研究、工程设计和运行模拟中。
OLGA 软件可以进行稳态模拟,其结果与动态模拟是一致的;也可以模拟油井、管道和工艺设备。
OLGA 软件以机理模型为基础,采用大量实验数据生成自己独有的数据库进行稳态和瞬态模拟计算。
PIPESYS 软件ASPEN 公司的 PIPESYS 多相流管网模拟分析软件是将PIPEFLO 和HYSYS 结合在一起,使之成为当今功能强大的管道计算软件。
PIPESYS 包括以下功能:模拟各种管网、单相流及多相流的计算、压力倒推计算。
通过HYSYS 和PIPESYS 的结合,可以研究管道的流量及其他条件的变化对整个管道系统的影响,计算管道的压力和温度分布,管道可以是海上或陆地,地形高度可以是简单或非常复杂。

连续气举单元多目标优化配气方法
连续气举单元多目标优化配气方法是一种在矿山施工中应用的优化配气方法。
它综合
考虑振动、煤尘和地质构造等因素,考虑到抽采气压、煤层破碎情况和防尘措施,对瓦斯
抽放进行优化配气。
连续气举单元多目标优化配气方法通过设定各个子目标的权重,综合考虑瓦斯、压力、煤尘等多个因素,通过灰色关联分析的两步求解过程,实现了连续气举单元的多目标优化
配气。
该方法首先利用灰色关联分析求解得出天然气、压力、煤尘释放等参数之间的灰色关
联系数,然后基于多目标抽放用途结合灰色关联系数,构建优化模型,最终得出连续气举
单元优化配气方案。
该方法可以有效改善煤层抽放状况,满足矿井安全高效抽放需求,有效改善煤层底流
稳定性,并使瓦斯释放更加合理。
同时,灰色关联分析求解出的灰色关联系数可以保证矿
山煤尘释放量控制在要求的合理水平之内,有效避免或者减少矿山煤尘污染的发生,保护
水土环境。
总的来说,连续气举单元多目标优化配气方法充分考虑瓦斯、压力、煤尘等多个因素,避免局部最优进而实现全局最优,通过灰色关联分析求解出灰色关联系数,得出多目标最
优配气方案,可以有效改善抽放状况,有效控制煤尘释放,保护水土环境。




CALPUFF高级培训教程-(多应用版)CALPUFF高级培训教程引言CALPUFF是一种大气传输和化学转化模型,广泛应用于空气质量评估、大气污染源解析和环境保护等领域。
本教程旨在为具有一定基础的CALPUFF用户,提供深入理解和应用CALPUFF模型的高级培训。
通过本教程的学习,用户将能够掌握模型的高级功能和技巧,更好地应用于实际问题和研究。
第一部分:CALPUFF模型简介1.1模型背景和特点1.采用拉格朗日粒子追踪方法,能够更准确地模拟污染物的传输过程;2.考虑了复杂地形和气象条件对污染物传输的影响;3.支持多种污染物物种的模拟,包括颗粒物、臭氧、二氧化硫等;4.提供了丰富的模型参数和化学反应机制,可适用于不同地区和不同污染问题。
1.2模型组成和功能CALPUFF模型由三个主要部分组成:预处理模块(CALPREP)、传输模块(CALPUFF)和后处理模块(CALPOST)。
预处理模块用于处理气象数据、地形数据和污染源数据,模型所需的输入文件。
传输模块是模型的核心部分,用于模拟污染物的传输和化学转化过程。
后处理模块用于处理模拟结果,浓度分布图、统计分析和报告等。
第二部分:高级功能和技巧2.1多尺度模拟CALPUFF模型支持多尺度模拟,能够同时模拟不同尺度的污染物传输过程。
用户可以根据研究需要选择适当的模拟尺度,例如局地尺度、区域尺度或全球尺度。
通过调整模拟尺度和网格分辨率,可以更精确地模拟污染物的传输和扩散过程。
2.2化学反应机制CALPUFF模型提供了多种化学反应机制,包括光化学反应、气相反应和颗粒物反应等。
用户可以根据研究需要选择适当的化学反应机制,并设置相应的反应速率和反应产物。
通过合理设置化学反应机制,可以更准确地模拟污染物的化学转化过程。
2.3污染源解析CALPUFF模型提供了污染源解析功能,能够分析不同污染源对污染物浓度的影响。
用户可以通过调整污染源的位置、排放量和排放高度等参数,模拟不同污染源对污染物浓度分布的影响。



优化设计混合惩罚函数法程序设计混合惩罚函数法(MPF)是一种常用于优化问题的算法,在多种应用领域中广泛使用。
通过引入惩罚函数来调整优化问题的目标函数,以求解约束优化问题。
以下是一个优化设计混合惩罚函数法的程序,我们将对其进行优化:```pythonimport numpy as np#定义目标函数def objective_function(x):return x[0]**2 + x[1]**2#定义约束函数def constraint_function(x):g1=x[0]+x[1]-1g2=-x[0]-x[1]-1return [g1, g2]#定义罚函数def penalty_function(g1, g2):return max(0, g1)**2 + max(0, g2)**2#定义设计混合惩罚函数法def mixed_penalty_function(x):obj = objective_function(x)cons = constraint_function(x)penalty = penalty_function(cons[0], cons[1])return obj + penalty#定义优化函数def optimize(:x0 = np.array([0, 0]) # 初始设计变量值sol = minimize(mixed_penalty_function, x0, method='BFGS')return sol.x#调用优化函数result = optimizeprint("优化结果:", result)```针对以上程序,我们可以进行以下优化:1.使用适当的优化算法:程序中使用了BFGS算法进行优化。
我们可以根据具体问题的特点选择合适的优化算法,如遗传算法、粒子群算法等。
不同的算法可能在不同的问题上表现更好。
2.优化设计变量的初始值:程序中初始设计变量的值为[0,0]。
有特殊安保任务的时候,讨薪民工为给政府施压而进行的堵路、非法上访、拉横幅、非法游行、跳楼示威、自焚等极端行为,严重危害了社会安全稳定。
4预防拖欠民工工资的对策建议4.1民工工资试行“月薪制”民工欠薪现象的发生与没有对农民工实行“月薪制”有一定关系。
要切实落实《劳动法》规定的“月薪制”,避免集中年终讨薪。
如果能采取坚决有效的措施,确保农民工按月足额领工资,年终讨薪大行动将不复存在。
要做到这一点,有必要建立工资保障金制度,比如,可以从工程项目中划拨一部分资金进入专门账户,成为农民工的预备工资,农民工按约定到银行领取,这样就减小了包工头等拖欠或者携款出逃的可能。
4.2建立温馨提示机制主要是通过制作“农民工维权温馨提示牌”,减少拖欠民工工资现象的出现。
由劳动保障部门结合本地实际情况为农民工制作“农民工维权温馨提示牌”,并要求建筑行业施工方将其悬挂在施工工地。
4.3增强劳动保障法律法规宣传力度通过组建由法制办、公安机关、检察院、人力社保系统等部门组成的法制宣讲小组,定时、深入地进入到各镇街、各用人单位进行劳动保障法律法规的宣讲宣传活动,通过“到镇街、下社区、入企业”全方位接受农民工的咨询,并作详细解答;印制、发放维权流程表、农民工基本权益条款等,用图文并茂的宣传单形式,让农民工更为直观地了解相关法律法规,进一步提高民工的法律意识。
4.4加大主动监察力度和劳动监察执法力度劳动保障部门要加强对用人单位特别是建筑工地的日常巡查,督促用人单位与农民工签订劳动合同,规范工资支付。
另外,劳动保障部门要加大主动监察力度,将农民工工资拖欠消灭在萌芽中。
一是推行使用工资表,监督工资发放情况。
落实劳动法要求企业按月按时支付农民工工资。
推行用工单位使用工资表,分别列出应发、实发、未发工资三部分,农民工和施工方(注:施工方应具有资质)要签字认可。
劳资双方签字后的工资表可以作为农民工获得劳动报酬的重要依据。
二是打击恶意欠薪。
劳动保障部门要做好拖欠民工工资的举报投诉工作,对拖欠农民工工资的投诉,实行“快接、快审和快结”。
天然气管网系统输配气运行优化研究3郑 凤33 李长俊(西南石油学院) 郑 凤 李长俊:天然气管网系统输配气运行优化研究,油气储运,2004,23(11)22~24。
摘 要 通过对天然气管网系统输配气过程中各种影响因素的分析,建立了天然气管网系统输配气运行方案优化的数学模型,采用复合形法对模型进行了求解,编制了计算软件,并应用于实际。
主题词 天然气 输配气管网 运行优化 复合形法一、优化输配气方案的数学模型及其求解〔1〕1、 数学模型管网系统运行优化就是对给定的管网系统,在一定的资源条件、不同销售价格以及不同的用户要求前提下确定输配气方案,使经营部门获得最大收益。
现将经营部门的收益作为目标函数,在满足资源、用户以及工艺技术约束条件下,确定进(分)气点的流量和压力。
求决策变量X =[P 1,Q 1,P 2,Q 2,…,P N n ,Q N n ]T,使目标函数式(1)在满足式(2)~式(6)约束条件下取最大值。
F =∑Nni =1S i Q i(1) Q i min ≤Q i ≤Q i m ax (i =1,2,…,N n )(2) P i m in ≤P i ≤P i m ax (i =1,2,…,N n )(3) P k ≤P k m ax (k =1,2,…,N P )(4) M =π4[P 2Q (1-C i Δh )-P 2Z ]D5λZR TL (1-C 1Δh 2)(5) ∑k ∈Ciαik M ik +Q i =0(6)式中 F ———目标函数; N n ———管网系统节点数; S i ———第i 节点购气和售气的费用系数,元/m 3; Q i ———第i 节点进(分)气量,分为正,进为负,无进分气量时为0,m 3/d ; 初始流量值与真实流量值的比较分析见表4。
表4 初始流量值与真实流量值的比较管段初始流量(m 3/h )手工计算值程序计算值实际流量(m 3/h )0250203.75217.681100157.585.052180168.75227.273 0-46.25 -32.32 4 011.25-47.27 为求解管网各个管段的初始流量值,在编程计算时,可以令K ij 为1,以保证求解的收敛性。
混合亚启发式算法求解带有热量损失的单吊机调度谢谢;周莉;郑勇跃【摘要】研究了钢铁企业物流系统中的一类单吊机调度问题.在板坯仓库中,为了最小化全部板坯的总热量损失,通过优化吊机的操作,以确定阻碍板坯的倒垛位置和目标板坯的拣选顺序.针对这个问题,建立混合整数线性规划模型求解小规模问题的最优解,对中大规模问题,提出混合亚启发式算法,该算法首先由贪婪启发式求得初始解进一步使用变深度邻域搜索策领略改进解的质量.数值计算实验结果表明,所提出的混合整数线性规划模型和混合亚启发式算法是有效的.【期刊名称】《沈阳大学学报》【年(卷),期】2019(031)002【总页数】6页(P107-112)【关键词】NP-难;启发式算法;单吊机;调度;热量损失【作者】谢谢;周莉;郑勇跃【作者单位】沈阳大学装备制造综合自动化重点实验室,辽宁沈阳 110044;中国标准化研究院社会信用研究室,北京100191;辽宁省检验检测认证中心事业发展中心,辽宁沈阳110032【正文语种】中文【中图分类】TP301.6本文研究了一类来自于钢铁生产企业中物流系统的吊机调度问题.每阶段板坯加工结束后,仓库作为存储板坯的缓冲区域,在这里,目标板坯(半成品或成品)需要由吊机操作拣选运输到下一阶段加工或客户端.仓库中的主要操作由吊机实施,包括将板坯运输到适合的位置,拣选客户的需求板坯,一旦板坯不能直接运输,先将压在其上方的阻碍板坯运输到其他位置等.在这些操作中,将阻碍板坯运输到其他位置的倒垛操作是非常消耗时间和能源的.倒垛操作的工作量占仓库总操作的一半以上[1].图1给出了板坯仓库的一个存储区域.钢铁企业板坯仓库中每个存储区域通常按行列堆放,大约276块板坯堆放成1~3行,1~92列.黑色和灰色分别表示需求板坯和倒垛板坯,虚线处表示该位置为空.每个区域由1台吊机操作.吊机可以由一个位置移动到另一个位置,意味着它的吊钩伴随着吊机不仅沿着平行的跨方向移动,而且还可以在跨之间的桥来回移动,两个方向可以同时进行.为了方便,本文中我们将吊钩看作吊机.板坯在每垛中按层堆放,一个堆放在另一个上面.图1 板坯仓库的存储区域Fig.1 A storage area in slab warehouse基于每垛存放的行列位置,图2以一垛为例,如果需求板坯在正上方,可以被直接吊走,否则需要先将阻碍板坯移动到其他地方以露出需求板坯.不同于Tang等[2-3]和Singh等[4]考虑的问题,根据存储区域的实际,本文考虑的倒垛板坯不需要再移动回原位,同时,所选取存放的位置要尽可能离倒垛板坯的原位置很近以减少倒垛时间,降低热量损失.由于原始的堆放可以保证每个板坯的位置,因此,板坯的倒垛位置充足.图2 板坯仓库的一垛板坯Fig.2 A slab stack in the slab warehouse对于每个需求板坯,吊机需要尽快地将其移动到指定位置.本文研究的问题就是确定需求板坯的移动顺序、倒垛板坯的移动位置最小化总温降损失.尽管倒垛板坯可以被移动到任一空位,为了避免进一步倒垛,本文不允许将倒垛板坯移动到需求板坯的上方,吊机的工作量包括倒垛和移动操作,该过程非常繁忙,是全部操作的瓶颈.因此吊机调度可以保证每个需求板坯及时被取出并减少热量损失.尽管已有一些相关文献研究钢铁仓库的吊机调度问题[5-9].但很少有研究考虑被吊物件热量损失的问题,求解问题的算法也仅仅是包括启发式规则和简单的邻域搜索策略,很少有尝试将贪婪算法和变深度邻域搜索策略组合对问题求解.Tang等[2]提出一个整数规划模型和两阶段启发式算法求解具有不同板坯族的问题.Tang等[3]研究了没有通用板坯的该问题并且提出遗传算法求解.Singh等[4]也提出一个改进的平行遗传算法,其中包含了一些新的遗传因子,以上研究的目标都是减少倒垛次数,在一定程度上节省了板坯操作的费用,Tang和Ren[10]也研究了板坯倒垛问题,提出了基于启发式的分部动态规划最小化吊机的总工作量.1 问题的定义和描述为了对问题建立数学模型,基于图1、图2,必要的符号说明如下.B为所有倒垛板坯的集合;R为所有需求板坯的集合;ri为需求板坯i的释放时间;P 为所有位置的集合;poi为板坯i的初始位置(i∈B∪R);tp,p′为从位置P到位置p′的装载移动时间;ep,p′为从位置P到位置p′的空载移动时间;pdi为需求板坯i的指定位置(i∈R);p0为吊机的初始位置.决策变量如下:Sj = 第j个装载移动的开始时间,j=1,2,…,(|B|+|R|);Cj = 第j个装载移动的完成时间,j=1,2,…,(|B|+|R|);i∈B, p∈P;i∈B∪R, j=1,2,…,(|B|+|R|).基于以上符号,混合整数规划模型表示如下.目标函数(1)表示所有需求板坯的总热量损失.假设热量损失曲线为l(t)=αe-γ t+β,其中α>0,γ∈(0,1),根据文献[11]可知,该曲线更适合实际生产,因此目标函数为最小化全部板坯的总热量损失其中hj=lj(rj)-lj(sj).约束(2)保证了吊机一次只能对一个板坯进行装载移动.约束(3)保证了每个需求板坯的取出和阻碍板坯的倒垛只能进行一次.约束(4)保证了一个需求板坯取出之前,它上方的阻碍板坯需要先被倒垛.约束(5)确保了阻碍板坯k被移动到的倒垛位置p最初由需求板坯i占用,则i首先在倒垛k 之前移动走.约束(6)保证了每个阻碍板坯仅倒垛到一个位置.约束(7)和(8)确保了在第(j-1)个装载移动的完工时间与第j个装载移动的开始时间之间有充足的空移动时间.这两个约束中的第(j-1)个装载移动分别表示对阻碍板坯的移动和需求板坯的移动.约束(9)确保了第一个装载移动仅仅在空吊机到达装载移动的初始位置后开始.约束(10)和(11)表示了吊机实施装载移动的开始和完成时间必须充足.这两个约束的装载移动分别表示阻碍板坯的移动和需求板坯的移动.约束(12)和(13)表示非负的二元变量.这个混合整数线性规划模型是线性的,因此可以使用CPLEX软件求解.然而,随着问题规模的扩大,CPLEX求解耗费大量时间,根据一次实际计划(大约超过20个位置),该软件就停止计算了,因此有必要对该问题提出有效的启发式算法.2 复杂性由于本文研究的问题复杂性不可知,因此使用归结的方法的证明该问题是强NP-难的.性质1 即使考虑一种最简单的情况:吊机的初始位置与需求板坯的目标位置相同,运输需求板坯的时间趋近于0,该情况也是强NP-难的.证明当这种情况发生时,只需要考虑对阻碍板坯进行倒垛.给定旅行商问题的实例,将旅行商看作单吊机,将城市看作阻碍板坯的位置.单吊机需要从它的初始位置运输通过每个倒垛板坯的位置后再回到初始位置,使得总完工时间最短,由于任意2个板坯位置预先已知,这种情况等价于已知的旅行商问题.由于旅行商问题是强NP-难的,因此,可知这种情况可解当且仅当旅行商问题可解.3 启发式算法及最坏性能分析在本节中,提出了一个混合亚启发式算法求解该问题.该算法在搜索不同的邻域空间与当前解的有效性上保持了一种平衡.分散搜索作为一种搜索机制结合了变深度邻域搜索的特点对解进一步搜索.第一步,首先使用贪婪启发式算法构成参考集,再根据解的组合机制产生新的解.之后通过使用变深度邻域搜索策略改进当前解,如果改进的解好于当前参考集的最坏解,则替换当前参考集里的解.3.1 参考集的建立第1步计算吊机对阻碍板坯从各自的位置到倒垛空位的距离,逐一按照非减的顺序排序;第2步逐一计算吊机当前位置到需求板坯的最近距离.3.2 解的组合机制令X和Y是2个基本子集里的解,表示解X中的板坯i,如果板坯i不在解中,则令= 0,根据如下等式确定新组合解的变量值.同样,令X,Y和Z表示3个基本子集的解.一般的解可由如下等式构建:3.3 解的改进3.3.1 邻域(1) 转换移动(Nshift).解的邻域转换定义为通过改变解内任意板坯的分配来获得.(2) 交互式移动(Nswap).解的邻域可以定义为通过交换解内两个板坯的分配来获得.3.3.2 变深度搜索策略(1) 通过搜索初始解的邻域Nswap获得.一旦找到局部最优解η(假设η是第一层的节点数)作为产生搜索树的第一层,搜索树的下一层按照如下方式建立:假设n1表示层d的节点数目;令d表示层数,M(d)为层d中解的候选列表;假设n1为候选解集M(d)的移动数目,n2为通过局部搜索产生的移动中最好的移动数目.(2) 探索n1个解的节点邻域Nswap中,n2为发现的最好解的数目.因此,在d+1层产生的解为N=n1×n2个.如果根节点处的解不能改进,则用该处的解作为最好的解.一旦全局解不能进一步改进,则搜索停止.4 计算结果为了估测所提出启发式算法的性能,计算实验基于实际生产数据.所有的算法使用VC++ 6.0编程并且运行在P4-3.00 GHz CPU以及内存为1G RAM的电脑上.MILP模型使用软件CPLEX 11.0版本求解.问题的实例使用如下数值:存储区域的全部位置|P|,区域的空间利用率U,所有需求板坯的数目|R|以及倒垛板坯的数目|B|.目标位置都在存储区域一行的一侧,举例说明,目标位置的选取从1到|R|,具体的位置从可能的位置中选取.如图1所示,同一垛中相邻两板坯的位置为1,相邻两垛中的距离为2,吊机沿两个方向的装载移动和空载移动的速度分别为v1=1 m/s,v2=2 m/s,λ1=2 m/s,λ2=4 m/s.上提下放的速度为μ=2.5 m/s.表1 2种所提出算法的性能比较Table 1 The performance for two proposed methods问题RBU(N0)PARD/%MILP模型混合亚启发式算法平均计算时间/sMILP模型混合亚启发式算法v1=1v2=2λ1=2λ2=4μ=2.5v1=1v2=2λ1=2λ2=4μ=50.5230.7120.90.5330.71 50.90.5340.7180.90.5350.7200.90.5230.7120.90.5330.7150.90.5340.7180.90. 5350.7200.92.832.913.413.505.805.984.534.905.275.314.365.185.225.484.67 4.908.019.024.325.115.33{2}6.249.55{10}12.211.922.132.142.473.313.443.08 3.153.453.653.353.783.133.322.392.524.32{1}5.572.923.133.52{2}3.856.12 {10}7.390.00200.02500.02700.03600.04600.16405.508025.37605474.5310.00283.01 408257.2620.00236000.0000.0030.02300.02900.06200.03700.04100.15704. 704042.21107337.5840.00276.86909353.3620.00236000.0000.003注: {·} 括号里的数字表示在时间限制内MILP模型不能最优求解的实例数目.对于每个实例,仓库的存储基于空间利用率以及N个可利用的位置.初始位置的选择考虑板坯的可行性,|R|个需求板坯存储在所有可行位置.尝试使用MILP模型求解小规模问题R,B,P分别为2,3,12.对于以上参数的各种组合,10个实例一组,分别使用MILP模型和混合亚启发式算法求解问题.设置10 h为使用MILP模型求解问题的时间限制,如果在这个时间内不能获得最优解,则记录下最好的可行解.由于MILP模型不能对每个实例求出最优解,使用下界LB,作为比较不同解质量的标准(Cmax-LB)/LB×100%.我们也将混合亚启发式算法与下界进行比较从而对所提出的算法进行估测.算法的平均相对偏差(ARD)和计算时间如表1.随着空间利用率的增加,MILP求解的时间大大增加了.当总的需求板坯数目和阻碍板坯数目达到8,空间利用率达到70%,时,使用MILP模型就不能在10 h内求得问题的最优解.对于一些小规模的例子,MILP模型可以求出问题的最优解.随着问题规模的扩大,MILP模型和下界之间的偏差变大,表明下界LB的质量看起来随着问题规模增大而恶化.这是因为,由于下界使用最短的移动时间估测实际的移动时间,然而,随着问题规模的增大两个位置之间的平均移动距离也增加了.混合亚启发式算法对任意测试的实例几乎都快速求解,解的质量距离最优解也不远.与MILP模型相比随着问题规模的增大,性能更加稳定.虽然随着问题规模的增加计算时间也增加了,求解70%空间利用率的实例时间长于低空间利用率如50%和高空间利用率90%,不同于MILP模型,求解的最长时间是空间利用率为90%的实例.或许是因为高空间利用率,对于阻碍板坯有非常少的空位,低空间利用率,则阻碍板坯较少可以帮助减少搜索时间.5 结论本文研究了钢铁企业板坯仓库的单吊机倒垛问题,目标函数为最小化被吊板坯总热量损失.针对这个问题,建立了混合整数规划模型,该模型用于最优求解小规模的问题,针对中大规模问题,进一步提出一个混合亚启发式算法,通过变深度邻域搜索策略改进初始解的性能.计算实验表明,所提出的方法可以有效的求解该问题.未来的研究将进一步扩展问题的模型和算法用于求解其他目标函数,如最小化总倒垛和总拣选的费用等.参考文献:【相关文献】[1]DE KOSTER RÉ,LE-DUC T,ROODBERGEN K J. Design and control of warehouse order picking: a literature review[J]. European Journal of Operational Research, 2007,182(2):481-501.[2]TANG L,LIU J,RONG A,et al. An effective heuristic algorithm to minimize stack shuffles in selecting steel slabs from the slab yard for heating and rolling[J]. Journal of the Operational Research Society, 2001,52(10):1091-1097.[3]TANG L,LIU J,RONG A,et al. Modelling and a genetic algorithm solution for the slab stack shuffling problem when implementing steel rolling schedules[J]. International Journal of Production Research, 2002,40(7):1583-1595.[4]SINGH K A,SRINIVAS,TIWARI M K. Modelling the slab stack shuffling problem in developing steel rolling schedules and its solution using improved parallel genetic algorithms[J]. International Journal of Production Economics, 2004,91(2):135-147.[5]谢谢,郑勇跃,李彦平. 工件和工具混合搬运的多吊机调度问题[J]. 沈阳大学学报(自然科学版), 2016,28(4):291-295.XIE X,ZHENG Y Y,LI Y P. Job and tool mixed transportation based multi-crane scheduling problem[J]. Journal of Shenyang University (Natural Science), 2016,28(4):291-295.[6]谢谢,郑勇跃. 带有机器卸载不延误约束的多吊机调度问题[J]. 沈阳大学学报(自然科学版), 2017,29(2):118-124.XIE X,ZHENG Y Y. Multiple crane scheduling with no-delay constraints for machineunloading[J]. Journal of Shenyang University (Natural Science), 2017,29(2):118-124. [7]TANG L X,XIE X,LIU J Y. Crane scheduling in a warehouse storing steel coils[J]. IIE Transactions, 2014,46(3):267-282.[8]XIE X,ZHENG Y Y, LI Y P. Genetic algorithm and its performance analysis for schedulinga single crane[J]. Discrete Dynamics in Nature and Society, 2015:1-12.[9]ZPFEL G,WASNER M. Warehouse sequencing in the steel supply chain as a generalized job shop model[J]. International Journal of Production Economics, 2006,104(2):482-501.[10]TANG L,REN H. Modelling and a segmented dynamic programming-based heuristic approach for the slab stack shuffling problem[J]. Computers & Operations Research, 2010,37(2):368-375.[11]BAI D Y,TANG L,SU M. A new machine scheduling problem with temperatureloss[C]∥Workshop on Knowledge Discovery and Data Mining, 2008:662-666.。