1.1 探索勾股定理(1)

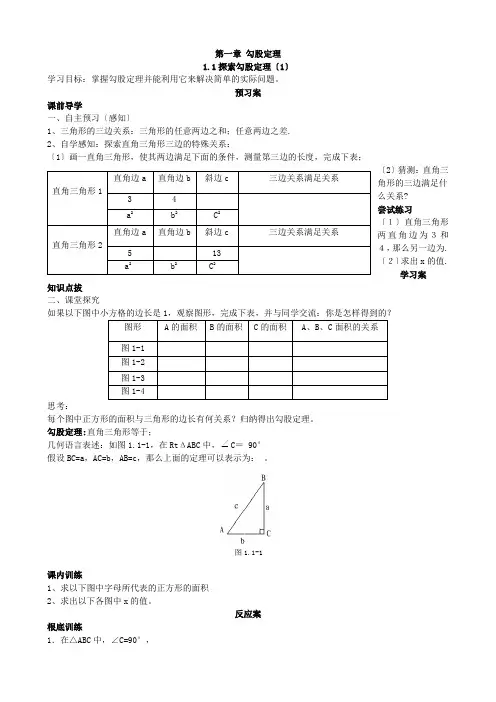
第一章 勾股定理 1.1探索勾股定理〔1〕学习目标：掌握勾股定理并能利用它来解决简单的实际问题。

预习案课前导学一、自主预习〔感知〕1、三角形的三边关系：三角形的任意两边之和；任意两边之差.2、自学感知：探索直角三角形三边的特殊关系：〔1〕画一直角三角形，使其两边满足下面的条件，测量第三边的长度，完成下表； 〔2〕猜测：直角三角形的三边满足什么关系? 尝试练习〔１〕直角三角形两直角边为３和４，那么另一边为. 〔２〕求出x 的值.学习案知识点拔 二、课堂探究如果以下图中小方格的边长是1，观察图形，完成下表，并与同学交流：你是怎样得到的？图形 A 的面积 B 的面积 C 的面积A 、B 、C 面积的关系图1-1 图1-2 图1-3图1-4思考：每个图中正方形的面积与三角形的边长有何关系？归纳得出勾股定理。

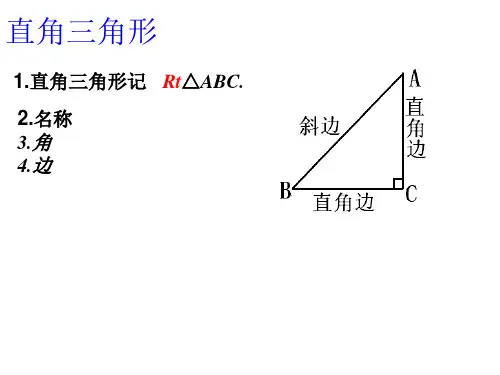
勾股定理:直角三角形等于；几何语言表述：如图1.1-1，在Rt ΔABC 中， C ＝ 90°假设BC=a ，AC=b ，AB=c ，那么上面的定理可以表示为： 。

课内训练1、求以下图中字母所代表的正方形的面积2、求出以下各图中x 的值。

反应案根底训练1．在△ABC 中，∠C=90°，直角三角形1直角边a 直角边b 斜边c 三边关系满足关系3 4a 2b 2C 2直角三角形2直角边a 直角边b斜边c 三边关系满足关系513a 2b 2C 2图1.1-1〔1〕假设BC=5，AC=12，那么AB=；〔2〕假设BC=3，AB=5，那么AC=；2．在Rt△ABC中,∠C=90°,AC=5,AB=13,那么BC=,该直角三角形的面积为。

3.假设直角三角形的两直角边之比为3：4，斜边长为20㎝，那么斜边上的高为。

拓展提高1.如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为7cm，那.么正方形A，B，C，D的面积之和为_______cm2C2.折叠长方形ABCD的一边AD，使点D落在BC边的F点处，假设AB=8cm，BC=10cm，求EC的长.。

1.1 探索勾股定理（1）一、课前预习1、正方形面积的计算公式，边长为5时，面积为多少？2、三角形两边分别是2,5第三边是c ，求第三边的取值范围.3、直角三角形两直角边为3、4求则第三边斜边的取值范围，斜边与这两条直角边的长度之间还有什么关系？二、新课学习 1、观察下面两幅图：2、填表：A 的面积（单位面积） B 的面积（单位面积） C 的面积（单位面积）左图 右图（3）你是怎样得到正方形C 的面积的？ 【小结】求面积常用方法： ____________________________（4）你能发现各图中三个正方形的面积之间有何关系吗？【结论】：以_______三角形两_______边为边长的小正方形的面积的和，等于以______边为边长的正方形的面积．AB CC BA思考：（1）若直角三角形两直角边长分别为a 、b ，斜边长为c ，则你能用直角三角形的边长a 、b 、c 来表示上图中正方形的面积吗？（2）你能发现直角三角形三边长度之间存在什么关系吗？★【勾股定理】如果直角三角形两直角边长分别为a 、b ，斜边长为c ，那么_________________ 即_______三角形两_____边的______和等于斜边的_______． 几何语言：∵在△ABC 中，∠____＝900∴____2＋____2＝____2三、典型例题及练习：例1、如图所示，一棵大树在一次强烈台风中于离地面9m 处折断倒下，树顶落在离树根12m 处. 大树在折断之前高多少？ 解：∵在△ABC 中，∠____ ＝900 ∴____2＋____2＝____2 即92 ＋122＝AB 2∴AB 2＝____ ∴AB ＝____∴大树在折断之前高 。

【跟踪练习】：1、如下图，今年的冰雪灾害中，一棵大树在离地面3米处折断，树的顶端落在离树杆底部4米处，那么这棵树折断之前的高度是 米.弦股勾ACBabc2、求图形中未知正方形的面积：3、若△ABC 中，∠C =90°，（1）若a =5，b =12，则c =________；（2）若a =6，c =10，则b =________；（3）若a ∶b =3∶4，c =10，则a =________，b =________.4.如图，阴影部分是一个半圆，则阴影部分的面积为多少？5.底边长6cm ，底边上的高为4cm 的等腰三角形的腰长为多少？6.如图所示的图形中，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为7cm ，则正方形A ，B ，C ，D 的面积的和是_________cm 2．1.1 探索勾股定理（2）一、课前复习：1、勾股定理：直角三角形_________________________ 几何语言：在△ABC 中，∵∠____ ＝900∴____2＋____2＝____22、在直角三角形ABC 中, ∠C =900,BC =12,CA =5,AB = ______.3、 如果直角三角形的一条直角边长为40，斜边长为41，那么另一条直角边的长为______.?2251002572577cmDACB二、典型例题：例1、飞机在空中水平飞行，某一时刻刚好飞到一个男孩子头顶上方4000米处，过了20秒，飞机距离这个男孩子头顶5000米，飞机每小时飞行多少千米？例2、受台风麦莎影响，一棵高18m 的大树断裂，树的顶部落在离树根底部6米处，这棵树折断后有多高？(提示：方程思想)三、课堂练习：1．某农舍的大门是一个木制的矩形栅栏，它的高为2m ，宽为1.5m ，现需要在相对的顶点间用一块木棒加固，木板的长为多少？2．我方侦查员小王在距离东西向公路400米处侦察，发现一辆敌方汽车在公路上疾驶，他赶紧拿出红外测距仪，测得汽车与他相距400米，10秒后，汽车与他相距500米，你能帮小王计算敌方汽车的速度吗？6米5000m4000mC B A500m400m C B A“路”4m3m3、一棵9m 高的树被风折断，树顶落在离树根3m 之处，若要查看断痕，要从树底开始爬多高？4．等腰三角形的腰长为13cm ，底边长为10cm ，则面积为（ ）． A ．30cm 2 B ．130cm 2 C ．120cm 2 D ．60cm 25、轮船从海中岛A 出发，先向北航行9km ，又往西航行9km ，由于遇到冰山，只好又向南航行4km ，再向西航行6km ，再折向北航行2km ，最后又向西航行9km ，到达目的地B ，求AB 两地间的距离.6、如图学校有一块长方形花铺，有极少数人为了避开 拐角走“捷径”，在花铺内走出了一条“路”．他们仅仅 少走了 步路（假设2步为1米），却踩伤了花 草．7、一个25m 长的梯子AB ，斜靠在一竖直的墙AO 上，这时的AO 距离为24m ，如果梯子的顶端A 沿墙下滑4m ，那么梯子底端B 也外移4m 吗？A BOCD3米9km AB9km 4km6km9km 2km8、△ABC中，∠C=900,AC=6,BC=8,沿AD折叠，使C点与AB边上的E点重合，求CD的长。

课题：1.1探索勾股定理 (1)【教学目标】(1) 经历“探索—发现—猜想—证明”的过程，进一步发展学生的推理能力.(2)掌握勾股定理,并能运用它解决一些实际问题1、课前练习：1、三角形的三个内角的比为1:2:3, 则这个三角形是____________ 三角形.2、一个三角形的其中两边为5和8 , 则第三边x 的取值范围是_______________3、等腰三角形的其中两边为5和1, 则这个三角形的周长为___________4、已知a = 3, b = 4, 则a 2 + b 2=______, ( a + b ) 2=________。

5、如果a 2 = 25, 则 a = _____2课前预习：（阅读书本P 1—5页）（1） 直角三角形三边有什么关系？你是怎样得到的? （2）勾股定理的内容？勾、股各是什么？【知识点一】出示投影（课本 P3 图1一2 1--3）并回答：1、观察图1一2中的左上图，正方形A 中有 个小方格，即A 的面积为个 面积单位。

正方形 B 中有 个小方格．即B 的面积为 个面积单位。

正方形 C 中有 个小方格，即C 的面积为 个面积单位。

2、你是怎样得出上面结果的？3、图 l 一2中，A 、B 、C 之间的面积之间有什么关系？_______________4、图1一 3中，A 、B 、C 之间有什么关系？【练习一】1、右图中字母所代表的正方形的面积,A=_____________B=______________【知识点二】小结：以直角三角形两直角边为边的正方形面积_____，等于以_____为边的正方形面积。

勾股定理: 直角三角边的________的平方和等于______的平方。

也就是说：如果直角三角形的两直角边为a 、b ，斜边为c 。

那么a 2+____=______【练习二】2、已知在Rt △ABC 中，∠C=90°，a=6 ,b =8 ,则c 2=__________a3、若一个直角三角形的的两条直角边长分别为3、4，以第三边的长向外作正方形，则这个正方形的面积是（ ）A 、25B 、49C 、 7D 、25或74、 已知在Rt △ABC 中，∠C=90°。

第一章勾股定理1.探索勾股定理（一）在两千多年前我国古算术上记载有“勾三股四弦五”.你知道它的意思吗？它的意思是说：如果一个直角三角形的两条直角边长分别为3和4个长度单位，那么它的斜边的长一定是5个长度单位，而且3、4、5这三个数有这样的关系：32+42=52.（1）请你动动脑筋，能否验证这个事实呢？该如何考虑呢？（2）请你观察下列图形，直角三角形ABC的两条直角边的长分别为AC=7，BC=4，请你研究这个直角三角形的斜边AB的长的平方是否等于42+72？测验评价等级：A B C ，我对测验结果（满意、一般、不满意）参考答案（1）边长的平方即以此边长为边的正方形的面积，故可通过面积验证.分别以这个直角三角形的三边为边向外做正方形，如右图：AC =4，BC =3,S 正方形ABED =S 正方形FCGH －4S Rt △ABC=(3+4)2－4×21×3×4=72－24=25即AB 2=25，又AC =4，BC =3， AC 2+BC 2=42+32=25 ∴AB 2=AC 2+BC 2（2）如图（图见题干中图）S 正方形ABED =S 正方形KLCJ －4S Rt △ABC =(4+7)2－4×21×4×7=121－56=65=42+722.探索勾股定理（二）下图甲是任意一个直角三角形ABC，它的两条直角边的边长分别为a、b,斜边长为c.如图乙、丙那样分别取四个与直角三角形ABC全等的三角形，放在边长为a+b的正方形内.①图乙和图丙中（1）（2）（3）是否为正方形？为什么？②图中（1）（2）（3）的面积分别是多少？③图中（1）（2）的面积之和是多少？④图中（1）（2）的面积之和与正方形（3）的面积有什么关系？为什么？由此你能得到关于直角三角形三边长的关系吗？测验评价等级：A B C，我对测验结果（满意、一般、不满意）参考答案①图乙、图丙中（1）（2）（3）都是正方形.易得（1）是以a为边长的正方形，（2）是以b为边长的正方形，（3）的四条边长都是c，且每个角都是直角，所以（3）是以c为边长的正方形.②图中（1）的面积为a2,(2)的面积为b2,(3)的面积为c2.③图中（1）（2）面积之和为a2+b2.④图中（1）（2）面积之和等于（3）的面积.因为图乙、图丙都是以a+b为边长的正方形，它们面积相等，（1）（2）的面积之和与（3）的面积都等于（a+b)2减去四个Rt△ABC的面积.由此可得：任意直角三角形两直角边的平方和等于斜边的平方，即勾股定理.2.探索勾股定理（二）班级：________ 姓名：________1.填空题(1)某养殖厂有一个长2米、宽1.5米的矩形栅栏，现在要在相对角的顶点间加固一条木板，则木板的长应取米.(2)有两艘渔船同时离开某港口去捕鱼，其中一艘以16海里/时的速度向东南方向航行，另一艘以12海里/时的速度向东北方向航行，它们离开港口一个半小时后相距海里.(3)如图1：隔湖有两点A、B，为了测得A、B两点间的距离，从与AB方向成直角的BC方向上任取一点C，若测得CA=50 m,CB=40 m，那么A、B两点间的距离是_________.图12.已知一个等腰三角形的底边和腰的长分别为12 cm和10 cm，求这个三角形的面积.3.在△ABC中，∠C=90°,AC=2.1 cm,BC=2.8 cm（1）求这个三角形的斜边AB的长和斜边上的高CD的长.（2）求斜边被分成的两部分AD和BD的长.4.如图2：要修建一个育苗棚，棚高h=1.8 m,棚宽a=2.4 m,棚的长为12 m,现要在棚顶上覆盖塑料薄膜，试求需要多少平方米塑料薄膜？5.如图3，已知长方形ABCD中AB=8 cm,BC=10 cm,在边CD上取一点E，将△ADE折叠使点D恰好落在BC边上的点F，求CE的长.测验评价结果：_____________；对自己想说的一句话是：______________________.参考答案1.(1)2.5 (2)30 (3)30米2.如图：等边△ABC 中BC =12 cm ，AB =AC =10 cm作AD ⊥BC ，垂足为D ，则D 为BC 中点，BD =CD =6 cm 在Rt △ABD 中，AD 2=AB 2－BD 2=102－62=64 ∴AD =8 cm ∴S △ABD =21BC ·AD =21×12×8=48(cm 2)3.解：(1)∵△ABC 中，∠C =90°，AC =2.1 cm ，BC =2.8 cm ∴AB 2=AC 2+BC 2=2.12+2.82=12.25 ∴AB =3.5 cm ∵S △ABC =21AC ·BC =21AB ·CD∴AC ·BC =AB ·CD ∴CD =ABBC AC ⋅=5.38.21.2⨯=1.68(cm)(2)在Rt △ACD 中，由勾股定理得： AD 2+CD 2=AC 2∴AD 2=AC 2－CD 2=2.12－1.682 =(2.1+1.68)(2.1－1.68)=3.78×0.42=2×1.89×2×0.21=22×9×0.21×0.21∴AD =2×3×0.21=1.26(cm)∴BD =AB －AD =3.5－1.26=2.24(cm)4.解：在直角三角形中，由勾股定理可得：直角三角形的斜边长为3 m,所以矩形塑料薄膜的面积是：3×12=36(m 2)5.解：根据题意得：Rt △ADE ≌Rt △AEF∴∠AFE =90°,AF =10 cm,EF =DE设CE =x cm ，则DE =EF =CD －CE =8－x 在Rt △ABF 中由勾股定理得： AB 2+BF 2=AF 2，即82+BF 2=102， ∴BF =6 cm∴CF =BC －BF =10－6=4(cm)在Rt △ECF 中由勾股定理可得： EF 2=CE 2+CF 2，即(8－x )2=x 2+42 ∴64－16x +x 2=x 2+16 ∴x =3(cm),即CE =3 cm参考例题［例1］如下图所示，△ABC 中，AB =15 cm ，AC =24 cm ，∠A =60°，求BC 的长.分析：△ABC 是一般三角形，若要求出BC 的长，只能将BC 置于一个直角三角形中. 解：过点C 作CD ⊥AB 于点D 在Rt △ACD 中，∠A =60° ∠ACD =90°－60°=30° AD =21AC =12(cm)CD 2=AC 2－AD 2=242－122=432， DB =AB －AD =15－12=3. 在Rt △BCD 中，BC 2=DB 2+CD 2=32+432=441BC =21 cm.评注：本题不是直角三角形，而要解答它必须构造出直角三角形，用勾股定理来解. ［例2］如下图，A 、B 两点都与平面镜相距4米，且A 、B 两点相距6米，一束光线由A 射向平面镜反射之后恰巧经过B 点.求B 点到入射点的距离.分析：此题要用到勾股定理，全等三角形，轴对称及物理上的光的反射的知识.解：作出B 点关于CD 的对称点B ′，连结AB ′，交CD 于点O ，则O 点就是光的入射点.因为B ′D =DB .所以B ′D =AC .∠B ′DO =∠OCA =90°， ∠B ′=∠CAO所以△B ′DO ≌△ACO (SSS ) 则OC =OD =21AB =21×6=3米.连结OB ，在Rt △ODB 中，OD 2+BD 2=OB 2 所以OB 2=32+42=52，即OB =5(米).所以点B到入射点的距离为5米.评注：这是以光的反射为背景的一道综合题，涉及到许多几何知识，由此可见，数学是学习物理的基础.。

1．为迎接新年的到来，同学们做了许多拉花布置教室，准备召开新年晚会，小刚搬来一架高为2.5米的木梯，准备把拉花挂到2.4米的墙上，则梯脚与墙角的距离应为米．2．如图1-1-1，小张为测量校园内池塘A，B两点的距离，他在池塘边选定一点C，使∠ABC＝90°，并测得AC长26m，BC长24m，则A，B两点间的距离为m．3．如图1-1-2，阴影部分是一个半圆，则阴影部分的面积为．（π不取近似值）4．底边长为16cm，底边上的高为6cm的等腰三角形的腰长为cm．5．一艘轮船以16km/h的速度离开港口向东北方向航行，另一艘轮船同时离开港口以12km/h的速度向东南方向航行，它们离开港口半小时后相距km．提高训练6．一个长为10m为梯子斜靠在墙上，梯子的顶端距地面的垂直高度为8m，梯子的顶端下滑2m后，底端滑动m．7．如图1-1-3所示的图形中，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为7cm，则正方形A，B，C，D的面积的和是cm2．8．已知Rt△ABC中，∠C＝90°，若14=+ba cm，10=c cm，则Rt△ABC的面积为（）．（A）24cm2（B）36cm2（C）48cm2（D）60cm29．如图1-1-4，分别以直角三角形的三边为边长向外作正方形，然后分别以三个正方形的中心为圆心，正方形边长的一半为半径作圆，记三个圆的面积分别为S1，S2，S3，则S1，S2，S3之间的关系是（）．（A）321SSS>+（B）321SSS=+（C）321SSS<+（D）无法确定10．暑假中，小明和同学们到某海岛去探宝旅游，按照如图所示的路线探宝. 他们登陆后先往东走8km，又往北走2km，遇到障碍后又往西走3km，再折向北走6km处往东一拐，仅走1km就找到了宝藏，则登陆点到埋宝藏点的直线距离为km．知识拓展12．如图1-1-7，有一块直角三角形纸片，两直角边AC＝6cm，BC＝8cm，现将直角边AC沿直线AD折叠，使它恰好落在斜边AB上，且与AE重合，求CD的长．BAE5米3米31．斜边为cm 17，一条直角边长为cm 15的直角三角形的面积是（ ）(A) 60 (B) 30 (C) 90 (D) 120 2. 等腰三角形的腰长为10,底长为12,则其底边上的高为( ) （A ）13 （B ）8 （C ）25 （D ）64 3. 已知一个Rt △的两边长分别为3和4，则第三边长的平方是（ ）（A ）25 （B ）14（C ）7 （D ）7或25 4. 在直角三角形ABC 中，斜边AB =2，则222AB AC BC ++=______.5. 直角三角形的三边长为连续偶数，则其周长为 .6. 如图1-1-8为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要____________米.提高训练7. 如图1-1-9，校园内有两棵树，相距12米，一棵树高13米，另一棵树高8米，一只小鸟从一棵树的顶端飞到另一棵树的顶端，小鸟至少要飞___________米.8. 如图1-1-10，小李准备建一个蔬菜大棚，棚宽4米，高3米，长20米，棚的斜面用塑料布遮盖，不计墙的厚度，请计算阳光透过的最大面积.9．伽菲尔德（Garfield ，1881年任美国第20届总统）利用两个全等的三角形拼成如图图形，Rt Rt ABC CDE △≌△，90B D ∠=∠=，且B C D ，，三点共线，证明了勾股定理（1876年4月1日，发表在《新英格兰教育日志》上），现请你尝试该证明过程．知识拓展10．如图，已知长方形ABCD 中AB =8 cm,BC =10 cm,在边CD 上取一点E ，将△ADE 折叠使点D 恰好落在BC 边上的点F ，求CE 的长.12. 已知，如图1-1-22，四边形ABCD 中，AB=3cm ，AD=4cm ，BC=13cm ，CD=12cm ，且∠A=90积。

第一章勾股定理1.1.1 探索勾股定理（一）学习目标：1．了解勾股定理的发现过程，掌握勾股定理的内容，会用面积法证明勾股定理。

2．培养在实际生活中发现问题总结规律的意识和能力。

3．介绍我国古代在勾股定理研究方面所取得的成就，激发学生的爱国热情，促其勤奋学习。

学习重点：勾股定理的内容及证明。

学习难点：勾股定理的证明。

学习过程：一、自主学习画一个直角边为3cm和4cm的直角△ABC，用刻度尺量出AB的长。

（勾3，股4，弦5）。

以上这个事实是我国古代3000多年前有一个叫商高的人发现的，他说：“把一根直尺折成直角，两段连结得一直角三角形，勾广三，股修四，弦隅五。

”这句话意思是说一个直角三角形较短直角边（勾）的长是3，长的直角边（股）的长是4，那么斜边（弦）的长是5。

再画一个两直角边为5和12的直角△ABC，用刻度尺量AB的长。

你是否发现32+42与52的关系，52+122和132的关系，即32+42_____52，52+122_____132，那么就有_____2+_____2=_____2。

(用勾、股、弦填空)对于任意的直角三角形也有这个性质吗？勾股定理内容文字表述：几何表述：二、交流展示例1、已知：在△ABC中，∠C=90°，∠A、∠B、∠C的对边为a、b、c。

求证：a2＋b2=c2。

分析：⑴准备多个三角形模型，利用面积相等进行证明。

⑵拼成如图所示，其等量关系为：4S△+S小正=S大正即4×21×＋﹝﹞2＝c2,化简可证。

⑶发挥学生的想象能力拼出不同的图形，进行证明。

⑷勾股定理的证明方法，达300余种。

这个古老而精彩的证法，出自我国古代无名数学家之手。

激发学生的民族自豪感，和爱国情怀。

例2已知：在△ABC中，∠C=90°，∠A、∠B、∠C的对边为a、b、c。

求证：a2＋b2=c2。

分析：左右两边的正方形边长相等，则两个正方形的面积相等。

左边S=_____________右边S=_____________左边和右边面积相等，即_________________________化简可得_______________________三、合作探究bbbccccaabbbaaccaabcc1．已知在Rt△ABC中，∠B=90°，a、b、c是△ABC的三边，则⑴c= 。

1.1 探索勾股定理（1）【学习目标】了解勾股定理的探索过程,掌握勾股定理． 【基础知识演练】1．在△ABC 中，若∠C =90°，则它的三边满足关系式a 2+b 2=c 2. 在此关系式中，涉及到三个量，利用方程的思想，可“知二求一”. (1)若a =3，b =4，则c =_________； (2)若 c =10，b =6，则a =_________；(3)若a ∶b =3∶4，c =20，则a =_________，b =_________. 2．已知等腰ABC ∆的腰AB ＝AC ＝10cm ，底边BC=12cm,则A∠的平分线的长是 cm.3．如图，在△ABC 中，∠C=900，AD 平分∠CAB ，AD=10cm ，AC=8cm ，那么D 点到直线AB 的距离是 cm. 4．如图，学校有一块长方形花铺，有极少数人为了避开拐角走“捷径”，在花铺内走出了一条“路”．他们仅仅少走了步路（假设2步为1米），却踩伤了花草．5．已知一个直角三角形的两边长分别为3和4，则第三边长的平方是（ ） A.25B.14C.7D.7或256．若线段a ，b ，c 能组成直角三角形，则它们的长度之比可能是（ ） A.2∶3∶4 B.3∶4∶6 C.5∶12∶13 D.4∶6∶77．在Rt △ABC 中，∠B ＝9O°，a 、b 、c 分别是∠A 、∠B 、∠C 的对边，且a ＝12，b ＝13，求c .D C BA8．请你取两个同样的直角三角板，并按如图所示摆放.(1)连结AE ，请你判断△ACE 和四边形ABDE 的形状.(2)设AB =CD =a ,BC =DE =b ,AC =CE =c ,请用两种不同的方法求四边形ABDE 的面积. （3）由（2）你能得到什么结论？DC B AE【思维技能整合】9．如果直角三角形的斜边与一条直角边的长分别是13cm 和5cm ，那么这个直角三角形的面积是 cm 2．10.如图，分别以直角△ABC 的三边AB 、BC 、CA 为直径向外作半圆，设直线AB 左边阴影部分面积为S 1，右边阴影部分面积为S 2，则（ ） A ．S 1 ＝S 2 B ．S 1 ＜S 2 C ．S 1＞S 2 D ．无法确定11．图中的螺旋形由一系列直角三角形组成，则以第n 个三角形的斜边长为边长的正方形的面积为 .12．请你作一个直角三角形ABC ，使它的两条直角边AB =6 cm,AC =8 cm.(1)请你先测量斜边BC 的长.（2）你能用其他方法探索这个直角三角形斜边的长吗？这个直角三角形的三边长有什么关系吗？（3）若使AB =AC =3 cm ，请你探索这个直角三角形的三边长有什么关系？A A A A O01231111【发散创新尝试】13.有一根70 cm 的木棒，要放在长、宽、高分别是50 cm 、40 cm 、30 cm 的木箱中，能放进去吗？请说明理由.【回顾体会联想】14.直角三角形三边之间有怎样的关系？生：如果直角三角形两直角边分别为a ，b ，斜边为c ，那么a ，b, c 的关系是 .即直角三角形两直角边的平方和等于 的平方.参考答案1． (1) 5.(2) 8.(3) 12,16 2．8 3．6 4．4 5．D 6．C 7．5 8．(1)∵△ABC ≌△CDE ,∴∠ACB =∠DEC ,而∠DCE +∠DEC =90°,∴∠ACB +∠DCE =90°,∴∠ACE =90°, ∴△ACE 为直角三角形.又∵∠ABC －90°=∠EDC , ∴四边形ABDE 为直角梯形. (2)方法一：S 梯形=21(AB +DE )·(BC +CD )=21(a +b )(a +b )=21(a +b )2.方法二：S 梯形=S △ABC +S △ECD +S △ACE =21ab +21ab +21c ·c =ab +21c 2.(3)∵S 梯形相等，∴21(a +b )2=ab +21c 2,∴a 2+b 2=c 2.9．30 10.A 11．n+112．(1)10 cm (2)AB2+AC2=BC2,另参考课本方法(3)AB2+AC2=BC2，探索方法同(2) 13.由下图可得，AA′=30 cm，A′B′=50 cm，B′C′=40 cm.△A′B′C′，△AA′C′都为直角三角形.由勾股定理，得A′C′2=A′B′2+B′C′2.在Rt△AA′C′中.AC′最长，则AC′2=AA′2+A′B′2+B′C′2=302+402+502=5000＞702.故70 cm的棒能放入长、宽、高分别为50 cm，40 cm，30 cm的大箱中.14.a2+b2=c2，斜边.。