数学建模——DVD在线租赁
- 格式:docx
- 大小:46.43 KB
- 文档页数:6



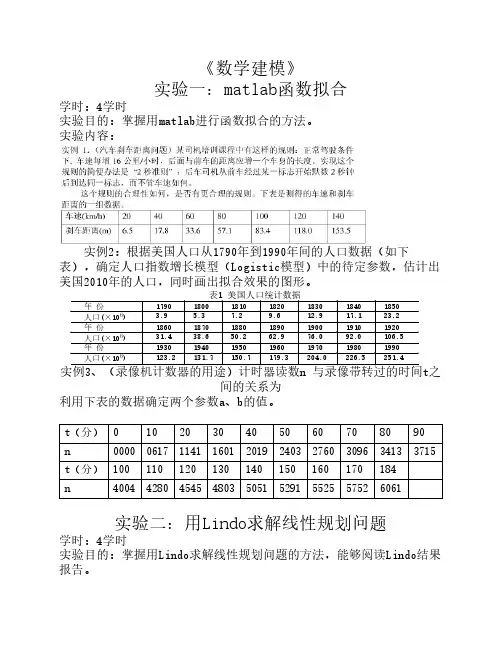




2005高教社杯全国大学生数学建模竞赛题目A题: 长江水质的评价和预测水是人类赖以生存的资源,保护水资源就是保护我们自己,对于我国大江大河水资源的保护和治理应是重中之重。
专家们呼吁:“以人为本,建设文明和谐社会,改善人与自然的环境,减少污染。
”长江是我国第一、世界第三大河流,长江水质的污染程度日趋严重,已引起了相关政府部门和专家们的高度重视。
2004年10月,由全国政协与中国发展研究院联合组成“保护长江万里行”考察团,从长江上游宜宾到下游上海,对沿线21个重点城市做了实地考察,揭示了一幅长江污染的真实画面,其污染程度让人触目惊心。
为此,专家们提出“若不及时拯救,长江生态10年内将濒临崩溃”(附件1),并发出了“拿什么拯救癌变长江”的呼唤(附件2)。
附件3给出了长江沿线17个观测站(地区)近两年多主要水质指标的检测数据,以及干流上7个观测站近一年多的基本数据(站点距离、水流量和水流速)。
通常认为一个观测站(地区)的水质污染主要来自于本地区的排污和上游的污水。
一般说来,江河自身对污染物都有一定的自然净化能力,即污染物在水环境中通过物理降解、化学降解和生物降解等使水中污染物的浓度降低。
反映江河自然净化能力的指标称为降解系数。
事实上,长江干流的自然净化能力可以认为是近似均匀的,根据检测可知,主要污染物高锰酸盐指数和氨氮的降解系数通常介于0.1~0.5之间,比如可以考虑取0.2(单位:1/天)。
附件4是“1995~2004年长江流域水质报告”给出的主要统计数据。
下面的附表是国标(GB3838-2002)给出的《地表水环境质量标准》中4个主要项目标准限值,其中Ⅰ、Ⅱ、Ⅲ类为可饮用水。
请你们研究下列问题:(1)对长江近两年多的水质情况做出定量的综合评价,并分析各地区水质的污染状况。
(2)研究、分析长江干流近一年多主要污染物高锰酸盐指数和氨氮的污染源主要在哪些地区?(3)假如不采取更有效的治理措施,依照过去10年的主要统计数据,对长江未来水质污染的发展趋势做出预测分析,比如研究未来10年的情况。

数学建模汽车租赁问题随着城市交通的发展和人们生活水平的提高,汽车租赁业务也逐渐兴起。
汽车租赁公司为个人和企业提供短期或长期租赁服务,给用户提供了更方便、灵活和经济的出行方式。
但是,如何合理安排租车方案,以最大程度地满足用户需求,同时又能使汽车租赁公司的利益最大化,是一个复杂的数学建模问题。
本文将探讨数学建模在汽车租赁问题中的应用。
首先,对于汽车租赁问题来说,主要涉及到两个关键因素:用户需求和汽车数量。
用户需求是指在一定时间内,用户对租车的需求量;汽车数量是指汽车租赁公司可提供的汽车数量。
为了使建模更具体,我们可以将时间分为若干时间段,每个时间段内的用户需求是一个已知的数值。
将用户需求和汽车数量通过数学表达式进行描述,建立数学模型成为解决问题的关键。
其次,在建立数学模型时,需要考虑到用户的租车时长。
用户可以根据个人需求选择租车的时间长度,汽车租赁公司通常会提供一天、一周或一个月的不同租赁方案。
因此,在数学建模中,我们需要根据用户的租车时长来确定租车费用,以便在最大程度满足用户需求的同时,实现汽车租赁公司的利益最大化。
另外,为了提高租车服务的质量,汽车租赁公司通常会对汽车进行维护和保养。
在数学模型中,我们可以引入维护和保养成本,以考虑到这一因素。
维护和保养成本可以通过每次租车的费用中加入一个折旧费用来体现。
通过适当调整租车费用,可以使得租车公司在满足用户需求的同时,合理分摊维护和保养成本,进而实现公司的利益最大化。
此外,汽车租赁公司还可以通过灵活制定不同类型的车辆租赁费用来满足不同用户的需求。
例如,对于高端汽车的租赁费用可以相对较高,而对于经济型汽车的租赁费用可以相对较低。
通过灵活制定不同类型的车辆租赁费用,可以吸引更多的用户选择租赁公司的服务,并进一步实现公司的利益最大化。
最后,在数学建模中,我们还可以考虑一些其他因素,如季节性需求的变化、市场竞争等。
通过分析这些因素对租车需求的影响,可以在制定租车方案时进行合理的调整,以更好地满足用户需求。

DVD在线租赁摘要本文讨论的是DVD在线租赁问题。
首先,运用了获取分布,得到其期望值的方法,对问卷调查结果和会员每月租赁DVD次数不同人数的百分比进行分析并求解,合理地解决了网站既要尽可能满足消费者的意愿,又要尽可能使成本相对低廉的矛盾;在此基础上又运用期望值和层次分析图相结合的方法,对在三个月内每个月可能出现租赁的人数进行分析,最终获得了合理的期望值。
其次,运用整数规划(0-1规划),根据100名会员的在线订单和网站手上20种DVD的现有张数,进行了定性地分配,并用分类规划,进行了定量地分配;再用定性反过来约束定量,并进行误差分析;最后,通过会员要求和网站的宏观调控,得出了最优的分配方案。
再次,围绕会员满意度最大这一目标,根据最优化原理导出的递推关系,利用等价变化,将整数规划转化为动态规划,从而决定出每种DVD合理的购买量,并对这些DVD进行合理的分配;再在计算机上用Lingo 软件对模型进行灵敏度检验。
最后,通过该模型对网站DVD在线租赁提出几点建议供网站参考。
模型的特点:1、运用期望值和层次分析图相结合的方法,既解决了期望值的不全面性,又解决了层次分析图无法定量化的问题,进而两种方法达到互补。
2、数据的转换,将表2中的值进行变换(10-c),(见附件[1])更科学地刻画了会员对DVD的偏爱程度。
(数字越大越偏爱程度越高)这样就解决了原始数字给计算带来困难的,使运算更明确、更方便。
3、根据最优化原理导出的递推关系,利用等价变化,将整数规划转化为动态规划,解决了整数规划求解大规模问题困难的问题。
【关键词】期望值层次分析图整数规划数据转换动态规划递推关系一、问题重述随着信息时代的到来,网络成为人们生活中越来越不可或缺的元素之一。
许多网站利用其强大的资源和知名度,面向其会员群提供日益专业化和便捷化的服务。
例如,音像制品的在线租赁就是一种可行的服务。
这项服务充分发挥了网络的诸多优势,包括传播范围广泛、直达核心消费群、强烈的互动性、感官性强、成本相对低廉等,为顾客提供更为周到的服务。
《数学建模》课程标准一、课程性质与目的要求数学建模课程是各专业的选修课,是数学科学联系实际的主要途径之一。
通 过该课程的学习,要使学生系统地获得数学建模的基本知识、基本理论和方法, 培养和训练学生的数学建模素质;要求学生具有熟练的计算推导能力,逻辑推理 能力,空间想象能力及综合运用所学知识分析和解决问题的能力;同时为使学生 适应现代社会奠定必要的基础。
要求掌握:(一)理论知识方面1. 根据理论结合实际的原则,要求学生重点掌握数学模型的建立和求解方法。
2. 基本掌握的内容: 初等模型、数学规划模型、微分方程模型、稳定性模型、 图论与网络模型、离散模型、概率统计模型、随机模拟等理论。
(二)实践技能方面要求学生重点掌握数据处理的一些基本方法,能够使用 Lindo/Lingo 求解各 种规划问题,使用 matlab 求解方程(组)、微分方程(组),进行数据拟合,参 数估计、假设检验、回归分析(特别是多项式回归)等概率问题。
二、学习用书教材:《数学建模与数学实验》(校本教材),谢珊主编,2010年,主要参考书:《数学模型》(第三版),姜启源等编,高等教育出版社,2004年,张珠宝主编,高等教育出版社,2005年《数学建模与数学实验》三、课程内容与考核标准(一)数学建模简介1, 教学目的与要求了解数学模型的概念。
掌握数学建模的一般步骤。
掌握人口增长模型的建立。
掌握 matlab函数拟合的方法。
2,教学内容(1)数学模型的概念及数学建模意义。
(2)介绍全国大学生数学建模竞赛。
(3)数学建模示例:人口增长模型。
3,考核要求l了解数学模型的概念及数学建模意义l会建立人口增长模型,并且能够用 matlab进行函数拟合,确定人口增长 模型中的参数。
(二)matlab入门1,教学目的与要求了解 matlab 的数组、矩阵、函数的定义与使用。
掌握 matlab 程序设计的基 本方法。
2,教学内容(1)介绍 matlab变量、数组、矩阵、表达式、流程控制、函数。
B题DVD在线租赁摘要本文在DVD在线租赁背景下,对DVD的租赁与归还,网方的购买与分配以及需求预测等相关问题做了模型研究。
首先,对题中给出的表示会员对各DVD的偏爱程度的偏好指数进行修正,提出了绝对满意度和相对满意度的合理定义。
第一问是在预知市场需求的情况下,确定各DVD采购量的问题。
本文首先建立了基于DVD租用次数限制的通用(General Model)模型(GM),结果见表1。
又从实际考虑,建立了以Poission过程模拟DVD归还过程的随机服务(Random Server Model)模型(RS),结果见表2。
第二问是对现有DVD的一次性分配问题。
本文建立了0-1整数线性规划模型(BIP)利用Lingo软件进行求解。
得到所有会员的最大绝对满意度之和为x=,给出了前30名会员的DVD获得情况(结E=,相对满意度0.916524746果见正文),并进一步给出1000个会员的个人相对满意度统计结果直方图。
第三问是多目标规划问题。
本文结合抽样统计的相关知识,建立了0~1规划模型。
在双目标规划的求解处理上,本文采取以满意度为限制条件,以碟的总量最小为目标进行规划的方式寻优,得出相对满意度与最小采购总量的关系曲线。
以利润最大和满意度最大的为目标,推荐给网管一种相对满意度为1,最小购买量为3047张DVD的具体采购方案(结果见正文)。
针对第四问,本文重点讨论了VIP会员的存在问题,VIP会员与普通会员的权重不同时的加权规划模型,和VIP会员有优先权情况下的分层规划模型,分别求出相关结果。
还简单讨论了会员的信用度、邮递时间、租赁规则等实际问题。
本文建模的过程中,每个环节都尽量考虑实际情况,所以模型的实际应用性和扩展性很强。
表1 GM模型求解结果DVD名称DVD1 DVD2 DVD3 DVD4 DVD5正常估计62503125 1563 782 313一个月50%的人看到悲观估计9000 4500 2250 1125 450乐观估计5000 2500 1250 625 250三个月95%的人看到正常估计3959 1980 1032 516 198表2RS模型求解结果DVD名称DVD1 DVD2 DVD3 DVD4 DVD5一个月内50% 5085 2543 1271 636 254三个月内95% 3921 1961 981 490 1961.问题重述在线DVD租赁问题。
2005年A题:长江水质的评价和预测编者按:本文用差分方程和回归分析的方法对问题作了正确、恰当的分析处理,结果合理。
具有一定的创造性。
编者按:本文构造了“s”型的变权函数,对属于不同水质类别的同种污染指标进行了动态加权;根据7个观测站的位置将干流分为8段,计算中间6段的排污量,将本段内所有污染源等效为一个段中央的连续稳定源,计算出其对该段段末观测站浓度的影响值。
以上两点具有独到想法。
全文思路正确。
表述清晰,假设可靠。
编者按:本文思路清晰,表述流畅,文章特点是:对不同水质指标用不同方法做标准化处理,再综合评价,主要污染源位置的确定和未来水质发展趋势预测等问题中均有完整的数学模型。
不足之处是,没有结合长江水质的整体评价。
编者按:本文结构完整,表述清晰。
自定义了综合污染指数,综合评价的思路有可取之处;分段考虑了主要污染源所在,对结果做了尝试性的解释,但未考虑两观测站间单位长度的污染量;用时间序列建模及处理污水量的规划问题思路清晰,但一次累加拟和模型中多项式指数的作用和含义不够明确。
值得一提的还有,最后的建议中与前面的结果相互印证。
编者按:本文思路清晰,论述疏密有致,许多细微之处稍显匠心。
构造了模糊评价指数可以很好的整合不同水质的影响因素;在未来10年的预测中,兼顾了长江流量与污水总量两者的共同影响(文中是对长江流量在不同置信水平的下限预测分析的)。
编者按:通过数学建模方法,本文对长江水域受污染的情况作出比较全面和量化的评价,对污染源进行了比较深入的分析,得出明确的结论,同时也对长江未来的水质情况和污水处理形势做出量化的科学预测。
特别值得推荐的是,作者对于污染源的特点和水质的不同性质进行了分类,对于控制水质与污水处理的策略具有积极的参考作用。
作为大学生能够在短时间内,在一个问题中拓出多处有创意的概念和方法,实在难能可贵。
虽然文章仍有不足,仍希望引起读者关注,以期提高中国大学生的创造性能力。
2005年B、D题:DVD在线租赁编者按:文章较好的理解了题目的意思,应用二项分布处理问题一,反映了作者对随机问题的理解和处理;以满意度最大为目标建立了0-1规划模型,利用Array Lingo软件求解得到会员的分配方案;问题三的解决是以分阶段建立双目标规划,虽没能完整解决该问题,但分析问题、解决问题的思想方法值得推荐。
2003年(A) SARS的传播问题(组委会)(B) 露天矿生产的车辆安排问题(吉林大学:方沛辰)(C) SARS的传播问题(组委会)(D) 抢渡长江问题(华中农业大学:殷建肃)2004年(A) 奥运会临时超市网点设计问题(北京工业大学:孟大志)(B) 电力市场的输电阻塞管理问题(浙江大学:刘康生)(C) 酒后开车问题(清华大学:姜启源)(D) 招聘公务员问题(解放军信息工程大学:韩中庚)2005年(A) 长江水质的评价和预测问题(解放军信息工程大学:韩中庚)(B) DVD在线租赁问题(清华大学:谢金星等)(C) 雨量预报方法的评价问题(复旦大学:谭永基)(D) DVD在线租赁问题(清华大学:谢金星等)2006年(A) 出版社的资源配置问题(北京工业大学:孟大志)(B) 艾滋病疗法的评价及疗效的预测问题(天津大学:边馥萍)(C) 易拉罐的优化设计问题(北京理工大学:叶其孝)(D) 煤矿瓦斯和煤尘的监测与控制问题(解放军信息工程大学:韩中庚)2007年(A) 中国人口增长预测(B) 乘公交,看奥运(C) 手机“套餐”优惠几何(D) 体能测试时间安排2008年(A)数码相机定位,(B)高等教育学费标准探讨,(C)地面搜索,(D)NBA赛程的分析与评价2009年(A)制动器试验台的控制方法分析(B)眼科病床的合理安排(C)卫星和飞船的跟踪测控(D)会议筹备2010年(A)储油罐的变位识别与罐容表标定(B)2010年上海世博会影响力的定量评估(C)输油管的布置(D)对学生宿舍设计方案的评价2011A题城市表层土壤重金属污染分析B题交巡警服务平台的设置与调度。
DVD在线租赁问题优化方案(田密万国)摘要本文依托现实网站DVD在线租赁预测、购买和分配方式,抽象简化出主要以网站购置量少、分配方式好以及会员满意度高为目标的数学模型,并通过合理简化假设进行需求预测,并建立优化模型。
问题一:我们建立DVD利用率数学模型,得到了至少50%在一个月内能够看到各种DVD至少需要的DVD张数分别为6250,3125,1563,782,313,以及三个月内能保证至95%的会员能够看到各种DVD至少需要的每种DVD的张数分别为3959,1980,990,495,198。
(具体见表一)问题二:首先通过对数据的分析定义了关系式:满意度f ij=11-偏爱度d ij,建立整数规划模型。
用Lingo解得最大满意度为24746,以及前三十名会员的分配方案(见表一),全部会员的分配方式(见附表DVDc.xls)。
问题三:要求DVD购置量最小与满意度最高是决策问题的关键,平衡DVD购置量和会员满意度,找到较好的购置方式及分配方案。
于是有两个目标:DVD购买总量最少,总满意度最大。
采用分层序列法将多目标规划转换为单目标规划,用Lingo编程解得DVD 购买总量2850张, 最大满意度为25650,以及分配方式(见附表DVD3c.xls)。
问题四:我们的想法是从网站最大化客户满意度与最大利润双目标的具体实现入手,可以考虑设立不同等级优先度的策略,以及减少DVD人为或运输破损等造成的损失,来共同提高会员整体满意度和实现效益最优。
关键词:整数规划模型,满意度,0-1规划,多目标规划,Lingo一、问题重述信息时代,网络发挥越来越重要的作用,许多网站利用强大资源和知名度为消费者提供专业便捷的服务。
音像制品的在线租赁即为其中一项,充分发挥了网络诸多优势,为顾客提供了周到的服务。
考虑在线DVD租赁问题。
顾客缴纳一定数量的月费成为会员,订购DVD租赁服务。
会员提交订单,网站根据现有的DVD数量和会员的订单进行分发,并基于其偏爱程度排序。
每个会员每月租赁次数和张数有限制。
会员在看完之后,将DVD寄回网站,就可以进行下次租赁。
考虑以下问题:1、网站预购新DVD,问卷调查得到愿意观看人数记录,并由历史数据得到租赁两次与租赁一次的人数之比。
考虑至少应准备多少张,能保证希望看到该DVD的会员中至少50%在一个月内能够看到该DVD;类似的,考虑在三个月内能保证至95%的会员能够看到该DVD至少需要的DVD张数。
2、根据网站现有DVD张数以及所需处理的会员订单,思考如何分配这些DVD,使会员得到最大满意度,并列出前三十位会员分别获得哪些DVD。
3、考虑表2(假设DVD数量为0),确定DVD的购买量以及分配方式,使一个月内95%的会员得到想看的DVD,并达到最大满意度。
4、针对问题四,我们从网站最大化客户满意度与最大利润双目标的具体实现入手,可以考虑设立不同等级优先度的策略,以及减少DVD人为或运输破损等造成的损失,来共同提高会员整体满意度和实现效益最优。
二、模型假设、的比例分配;1、只存在每月租借一次和每月租借两次两类会员,且符合40%60%2、会员每月至少租借一次DVD,每次只能租借三张DVD,且三张不同;3、一个月借两次的人必须在第一次借的DVD归还之后才能再接第二次;4、每月只借一次的会员在月末才归还所借的DVD,所以这部分DVD不能再借给其他会员;5、不同DVD的需求与分配独立,之间没有关联性;6、某张DVD被会员还回后,可在当天配送给其他需要的会员;7、DVD的分配量决定其购置量;8、会员满意度与其在一个分配周期内租借到其想看DVD的具体时间无关;三、符号说明1、a j为第j(j=1,2…5)种DVD应准备的数量;2、b j为希望看到第j种DVD的人数;3、c ij等于1表示分配给会员i第j种DVD,反之不分配(i=1,2,…,1000,j=1,2,3…100);4、d ij表示会员i对第j种DVD的偏爱度(i=1,2,3…1000,j=1,2,…,100);5、e j 表示第j 种DVD 现有的数量;6、f ij 为会员i 对第j 种DVD 的满意度(i=1,2,3…1000,j=1,2,3…100);7、g i 表示会员i(i=1,2,3…1000)是否得到三张DVD ,若得三张,则其为1,反之为0; 8、x j 代表第j 中DVD 应该购买的数量,z 为购买的DVD 总数,y 为会员总满意度; 9、excel 文件:表DVDed 是偏爱度数据; 表DVDf 是满意度数据;表DVDc 是问题二DVD 的分配方案;表DVD3c 是模型三解得的DVD 分配方案和每种DVD 应购买数量。
四、问题分析与模型建立(一)模型一从实际情况看,每个会员每月最多借两次,根据历史数据,每月租借一次和两次的会员分别占总会员人数的40%和60%,即每个月借出去的DVD 有60%的人在本月会归还,还能借给他人,即第一次借出a j ,则归还后还能再借给其他60%a j 人,在一个月中使需要每种DVD 的会员中有50%的人可以借得DVD ,即至少有50%b j 人借得需要的DVD ;引入下面的结构图辅助分析:图 1对上面的租借结构图可以得出:①在一个月中要使希望看到该DVD 的会员中至少有50%可以看到该DVD ,则a,b 应满足:min=∑a j 5j=1; a j +60%a j ≥50%b j②在三个月中使希望看到该DVD 的会员中至少有95%的人可以看到该DVD ,由于每个月是一个周期,所以第二个月、三个月的情况与第一个月类似,所以a,b 应满足:min=∑a j 5j=1; 3(a j +60%a j )≥95%b j由Lingo 可以解出模型一的结果见表一:表一DVD 名称 DVD1 DVD2 DVD3 DVD4 DVD5 ①购置张数 6250 3125 1563 782 313 ②购置张数39591980990495198具体程序参考附录一(二)模型二要使会员的满意度最高,即使会员总的偏爱度最高,分析表中的数据可知表中所给的数据不代表订单的数量,而是代表偏爱程度,到数据为零代表该会员没有下订单,不为零代表有订单,而数据越小代表偏爱度越高,观察表中的数据可知:偏爱度最小为10,最大为1,为了方便计算,我们将偏爱度转化为满意度,则:最小满意度为1,最大满意度为10:即当偏爱度部位0时:满意度=11-偏爱度;当偏爱度为0时满意度为0。
同时分配DVD 时需满足:当会员无订单时不能给其分配DVD ,必须够三张才能给其分配,计算表中的DVD 现有数量总和可知,共有3007张DVD ,可以满足1000人每人三张。
目标函数:Max=∑∑c ijf ij 100j=11000i=1;分配原则必须满足如下条件:现有的DVD 数量约束: ∑c ij 1000i=1≤e j (j=1,2,3…100); 每人是否得到三张DVD 约束:∑c ij 100j=1=3g i (i=1,2,3…1000); 满意度计算:当 d ij =0时,f ij =0;当d ij >0时,f ij =11- d ij ; 综上,数学模型为:Max=∑∑c ijf ij 100j=11000i=1;约束条件:∑c ij 1000i=1≤e j (j=1,2,3…100); ∑c ij 100j=1=3g i (i=1,2,3…1000);当 d ij =0时,f ij =0;当d ij >0时,f ij =11- d ij ;运用Lingo 软件编程可求得前三十名会员的分配方案如下表二:表二会员编号1 2 3 4 5 6 7 8 9 10 DVD 编号 41 44 50 18 66 53 66 35 78 55 98 62 80 41 68 66 81 71 100 85 会员编号DVD 编号 59 2 21 23 13 10 47 41 66 45 63 31 78 52 52 84 51 60 84 61 66419689859767788689会员编号DVD 编号50 55 81 41 69 68 58 34 30 62 53 57 95 76 94 95 78 82 55 98全部会员的分配方案见表DVDc.xls ;(三)模型三购买DVD 的数量越少越省钱,但是不能太少,如果不能满足一定的会员满意度,则会对公司后期发展造成不利后果,所以应该在购买DVD 的数量和会员满意度之间找到一个平衡,既能使购买的DVD 数量尽可能的少,又能使会员满意度尽可能的大。
于是该模型有两个目标函数:满意度:max y=∑∑c ij 100j=1f ij 1000i=1DVD 总购买量:min z=∑x j 100j=1; 约束条件:购买与分配的DVD 数量约束:∑c ij 1000i=1≤x j , j=1,2,3…100; 会员得到三张DVD 约束:∑c ij 100j=1=3g i , i=1,2,3…1000; 95%的会员得到需要的DVD 约束:∑g i 1000i=1=95%×1000; 0,1约束:g i =0或1;c ij =0或1。
综上,数学模型为:max=∑∑c ij 100j=1f ij 1000i=1 , min= ∑x j 100j=1;约束条件:∑c ij 1000i=1≤x j , j=1,2,3…100; ∑c ij 100j=1=3g i , i=1,2,3…1000; ∑g i 1000i=1=95%×1000; g i =0或1;c ij =0或1。
由于多目标函数用Lingo 不能直接求解,所以运用分层序列法求解:先不考虑总满意度最大,求得DVD 的最小购买量z=2580,再以求得的DVD 的最小购买量z=2580为约束条件求得最大满意度25650;然后再不考虑DVD 的最小购买量,求得总的最大满意度25650,以最大满意度为约束条件,求DVD 的最小购买量2850。
综上可知,最大满意度为25650,购买的DVD 数量为2850时可以使一个月有95%的会员能得到希望的DVD 。
具体程序见附录三。
(四)模型四从网站最大化客户满意度与最大利润双目标的具体实现入手,可以考虑根据会员缴纳会费多少设立不同等级优先度的策略,或者通过监管力度加大对流通环节因DVD 人为或运输破损等造成的损失,来共同提高会员整体满意度和实现效益最优。
五、模型评价1.问题一中采用DVD 利用率的简化模型,算法思想清晰,便于求解;2.问题二中采用的0-1规划模型,运用Lingo 较快解出了最优解3.问题三中采用0-1规划及多目标模型求解,为网站平衡会员满意度和DVD 购置量提供了量化依据。