数电基本逻辑电路

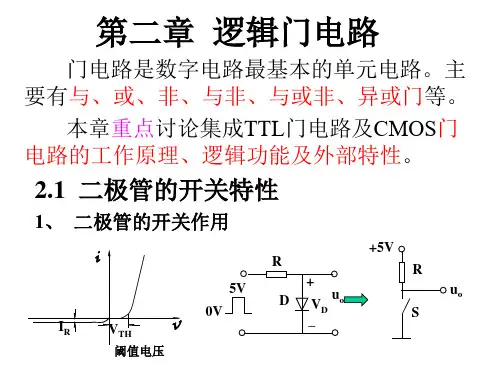
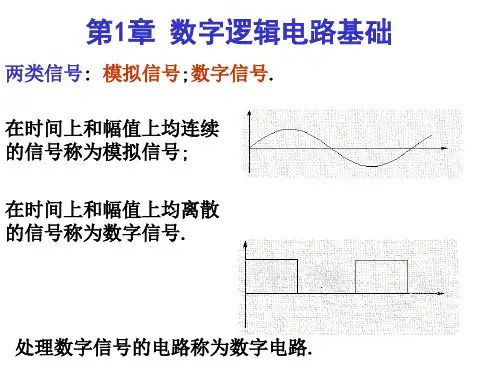
数电逻辑门电路逻辑门电路是数字电路中常见的一种电路结构，用于处理不同的逻辑运算和控制信号。

逻辑门电路通常由不同类型的逻辑门组成，如与门、或门、非门、异或门等。

在这篇文章中，我们将介绍几种常见的逻辑门电路以及它们的应用。

1. 与门电路与门电路是最基本的逻辑门之一，其功能是将两个输入信号进行逻辑与运算，输出结果为如果两个输入信号同时为高电平时输出高电平，否则输出低电平。

与门电路通常用于逻辑运算和控制信号的处理，比如电脑中的逻辑电路、开关控制等。

2. 或门电路或门电路是另一种常见的逻辑门，其功能是将两个输入信号进行逻辑或运算，输出结果为如果任一输入信号为高电平时输出高电平，否则输出低电平。

或门电路也广泛应用于逻辑运算和控制信号处理中，例如电脑中的逻辑电路、开关控制等。

3. 非门电路非门电路是一种单输入单输出的逻辑门，其功能是将输入信号取反输出，即如果输入信号为高电平则输出低电平，如果输入信号为低电平则输出高电平。

非门电路通常用于信号反转、逻辑反相等应用。

4. 异或门电路异或门电路是一种常见的逻辑门，其功能是将两个输入信号进行逻辑异或运算，输出结果为如果两个输入信号不相同则输出高电平，否则输出低电平。

异或门电路在数字电路设计中经常被使用，例如数据的误码检测、加法器电路等。

以上是几种常见的逻辑门电路，下面我们将介绍一个简单的逻辑门电路示例：4位全加器电路。

4位全加器电路是由4个异或门、3个与门和1个或门组成的逻辑电路，用于实现4位二进制数的加法运算。

该电路的原理是将两个4位二进制数相加，得到和输出以及进位输出。

当输入信号为A3-A0、B3-B0时，输出信号为S3-S0代表和值，C代表进位位。

在4位全加器电路中，每个异或门接收两个输入信号A和B，输出一个异或运算结果；每个与门接收三个输入信号A、B和C_in，输出一个与运算结果；一个或门接收四个输入信号S0-S3，输出一个或运算结果。

将这些逻辑门按照接线图正确连接，就可以实现全加器电路的功能。

数电逻辑门电路
逻辑门电路是数字电路中最基本的组成部分，它执行基本的逻辑运算，如 AND、OR、NOT 等。

常见的逻辑门
•AND 门：只有当所有输入都为高电平时，输出才为高电平。

•OR 门：只要有一个输入为高电平时，输出就为高电平。

•NOT 门：当输入为高电平时，输出为低电平，反之亦然。

•NAND 门：与 AND 门相同，但输出取反。

•NOR 门：与 OR 门相同，但输出取反。

•XOR 门：只有当输入不同时，输出才为高电平。

•XNOR 门：只有当输入相同时，输出才为高电平。

逻辑门符号
每个逻辑门都有一个标准符号，用于表示其功能和输入/输出关系。

逻辑门特性
•逻辑电平：逻辑门通常使用高电平和低电平表示二进制信号。

•传递延迟：逻辑门之间有延迟时间，称为传递延迟。

•扇出：逻辑门可以驱动多个其他逻辑门，其数量称为扇出。

•功耗：逻辑门消耗功率，这取决于其尺寸、类型和开关频率。

逻辑门应用
逻辑门电路用于各种数字系统中，包括：
•计算机
•智能手机
•数字仪表
•控制系统
•数据通信
逻辑门实现
逻辑门电路可以通过以下方式实现：
•分立器件：使用晶体管、电阻器和二极管等分立器件构建。

•集成电路（IC）：将多个逻辑门集成到一个单一的 IC 芯片中。

•现场可编程门阵列（FPGA）：提供可编程逻辑，允许用户配置自定义逻辑门电路。

第6次课三种基本逻辑关系、分立元件门电路、复合逻辑门电路●本次重点内容：1、与、或、非三种基本逻辑关系及真值表、逻辑表达式、门电路逻辑符号。

2、分立元件门电路的工作原理。

3、复合逻辑关系：与非、或非、与或非、异或、同或的真值表、逻辑表达式、门电路逻辑符号。

●教学过程6.1三种基本逻辑关系一、与逻辑关系所谓与逻辑关系：就是指决定某事件结果的所有条件全部具备，结果才能发生，而只要其中一个条件不具备，结果就不能发生，这种逻辑关系称为与逻辑关系。

与逻辑示意如图6-1所示：用A，B表示条件，即开关的状态；用Y表示结果，即表示灯的亮、灭状态。

图6-1 与逻辑示意图开关：“1”表示开关闭合，“0”表示开关断开。

灯：“1”表示灯亮，“0”表示灯灭。

根据所有可能的开关组合状态与灯亮、灭的对应关系，可以列出真值表。

如表6-1所示。

表6-1 与逻辑真值表由表6-1可以得出“与”逻辑关系为“有0出0，全1出1”。

与门是实现与逻辑关系的电路，其逻辑符号如图6-2所示：图6-2 与逻辑符号二、或逻辑—在A，B等多个条件中，只要具备其中一个条件，事件就会发生；只有所有条件均不具备时，事件才不会发生，这种因果关系称为或逻辑关系。

或逻辑示意如图6-3所示：图6-3 或逻辑示意图经分析开关A，B的闭合情况，可以列出或逻辑真值表如表6-2所示：表6-2 或逻辑真值表由上表6-2可以得知或逻辑功能为“有1出1，全0出0”。

或门是实现或逻辑关系的电路，其逻辑符号如图6-4所示。

图6-4或逻辑符号三、非逻辑：决定事件结果只有一个条件，当条件具备时，结果就不发生；当条件不具备时，结果就发生。

这种因果关系称为非逻辑关系。

非逻辑示意如图6-5所示。

当开关A闭合时，灯Y灭；当开关A断开时，灯Y亮。

可见，对灯亮来说，开关A闭合是非逻辑关系。

图6-5非逻辑示意如图经分析可以列出或逻辑真值表6-3。

表6-3 非逻辑真值表由上表可以得知非逻辑功能为“是0出1，是1出0”。

数电逻辑16个公式(二)数电逻辑16个公式1. 与门公式与门是最基本的逻辑门之一，其公式为：Y = A * B。

例解：假设A = 1，B = 0，则根据与门公式，Y = 1 * 0 = 0。

2. 或门公式或门是另一种基本的逻辑门，其公式为：Y = A + B。

例解：若A = 1，B = 0，则根据或门公式，Y = 1 + 0 = 1。

3. 非门公式非门也称为反相器或否定器，其公式为：Y = !A。

例解：当A = 1时，则根据非门公式，Y = !1 = 0。

4. 异或门公式异或门也称为互斥或门，其公式为：Y = A ⊕ B。

例解：如果A = 1，B = 0，则根据异或门公式，Y = 1 ⊕ 0 = 1。

5. 与非门公式与非门是由与门和非门组成的，其公式为：Y = !(A * B)。

例解：假设A = 1，B = 0，则根据与非门公式，Y = !(1 * 0)= !0 = 1。

6. 或非门公式或非门是由或门和非门组成的，其公式为：Y = !(A + B)。

例解：如果A = 1，B = 0，则根据或非门公式，Y = !(1 + 0)= !(1) = 0。

7. 同或门公式同或门是由异或门和非门组成的，其公式为：Y = !(A ⊕ B)。

例解：假设A = 1，B = 0，则根据同或门公式，Y = !(1 ⊕ 0)= !(1) = 0。

8. 三输入与门公式三输入与门是由三个输入信号组成的，其公式为：Y = A * B * C。

例解：如果A = 1，B = 0，C = 1，则根据三输入与门公式，Y = 1 * 0 * 1 = 0。

9. 三输入或门公式三输入或门也称为多输入或门，其公式为：Y = A + B + C。

例解：假设A = 1，B = 0，C = 1，则根据三输入或门公式，Y = 1 + 0 + 1 = 1。

同样由三个输入信号组成的同或门公式为：Y = !(A ⊕ B ⊕ C)。

例解：如果A = 1，B = 0，C = 1，则根据三输入同或门公式，Y = !(1 ⊕ 0 ⊕ 1) = !(0) = 1。

实验一：基本门电路的应用
一． 实验目的
1. 熟悉基本门电路特别是与非门的使用；
2. 学会用与非门实现简单的逻辑函数； 二． 实验原理
1. 与非门实现与运算
AB AB F ==1 该逻辑函数的逻辑电路如图1所示：
图1
2. 与非门实现或运算
B A B A B A F =+
=+=2
该逻辑函数的逻辑电路如图2所示：
图2
3．与非门实现异或运算
1(悬空)
1F
A B A
B 2F
AB
B AB A AB B AB A AB B AB A B A B A F 3=+=+=+=
该逻辑函数的逻辑电路如图3所示：
图3
三． 实验内容
1. 输入端A 接f=1kHz,Vpp=5v 的方波,偏移量
2.5v 。

B 端接开关。

输出端接示波器的通道二，通道一接输入端信号。

2. 按照图1搭建电路，分别在B 端是开和关两种状态时，并电路进行测试；
3. 按照图2搭建电路，分别在B 端是开和关两种状态时，并电路进行测试；
4. 按照图3搭建电路，分别在B 端是开和关两种状态时，并电路进行测试； 四． 实验结果 1.AB F =1
A
B
3
F A
B为关 B为开 2.B
A
F+
=
2
B为关 B为开3.B
A
B
A
F
3
+
=
B为关 B为开。