2018届北师大版(文科数学)算法初步单元测试

2.3.2 循环语句(建议用时：45分钟)[学业达标]一、选择题1．观察下面的算法语句：S＝0For i＝1 To 100S＝S＋iNext输出S.该算法语句的功能是( )A．求1×2×3×4×…×100的值B．求1＋2＋3＋4＋…＋100的值C．求1×3×5×…×99的值D．求1＋3＋5＋…＋99的值【解析】根据For循环语句的作用可知通过累加求式子1＋2＋3＋4＋…＋100的值．【答案】 B2．以下程序S＝0For x＝－1 To 11S＝x*xNext输出S.该程序输出结果是( )A．－1 B．11C．100 D．121【解析】由For语句的算法特点可知，S＝11×11＝121.【答案】 D3．下列程序的运行结果为( )i＝0S＝0Doi＝i＋1S＝S＋iLoop While S＜＝20输出i.A．5 B．6C．7 D．8【解析】由于0＋1＋2＋3＋4＋5＝15,0＋1＋2＋3＋4＋5＋6＝21，所以输出i＝6.【答案】 B4．下列程序中循环语句的循环终止条件是( )m＝1Dom＝m＋3Loop While m＜10输出m.A．m＝10 B．m＜10C．m＞10 D．m≥10【解析】当m＜10时不成立，即m≥10时循环终止．【答案】 D5．运行下面的程序时，Do循环语句的执行次数是( )N＝0DoN＝N＋1N＝N*NLoop While N＜20输出N.A．3 B．4C．15 D．19【解析】0＜20,1＜20,2×2＜20,5×5＞20，循环结束．故While循环语句共执行了3次，所以选A.【答案】 A二、填空题6．以下算法语句：S＝1k＝13DoS＝S*kk＝k－1Loop While ________输出S.若语句运行的结果是S＝156，则横线处应填入的k的条件是________．【解析】第一次循环是S＝1×13＝13，第二次循环是S＝13×12＝156，故k的条件应是k＞＝12或k>11.【答案】k＞＝12或k>117．执行下面的算法语句后输出的结果是________．S＝0For i＝1 To 4S＝S*i＋lNext输出S.【解析】当i＝1时，S＝0×1＋1＝1；当i＝2时，S＝1×2＋1＝3；当i＝3时，S＝3×3＋1＝10；当i＝4时，S＝10×4＋1＝41，循环结束，输出S，所以输出S的值为41.【答案】418．算法语句j＝1Doj＝j＋1Loop While j*j＜100j＝j－1输出j.运行的结果是________．【解析】①当j＝1时，j＝2,2×2＜100；②j＝3,3×3＜100；③j＝4,4×4＜100；…；⑧j＝9,9×9＜100；⑨j＝10,10×10＝100，结束循环，此时输出j－1＝9.【答案】9三、解答题9．据下列框图写出对应算法语句．图2­3­3【解】S＝0i＝1DoS＝S＋ii＝i＋1Loop While i＜＝1000输出S.10．给出以下10个数：4,10,70,33,95,74,29,17,60,30.要求将大于40的数找出来，画出求解该问题的算法框图，并写出程序．【解】算法框图如图所示：i＝1Do输入xIf x＞40 Then输出xEnd Ifi＝i＋1Loop While i＜＝10[能力提升]1．如果算法语句运行后输出的结果是720，则在横线处应填入的正整数为( )A ．9B ．8C ．7D ．6【解析】 第一次执行循环体，S ＝1×10＝10，t ＝9，第二次执行循环体，S ＝10×9＝90，t ＝8，第三次执行循环体，S ＝90×8＝720，t ＝7，依题意，循环结束，根据Do Loop 语句的要求，条件不满足时，结束循环，所以条件应为t >7，故选C.【答案】 C2．下列算法运行后输出的结果为( )i ＝7S ＝0DoS ＝S ＋ii ＝i －1Loop While S <15输出i .A ．1B ．2C ．3D ．4【解析】 执行第一次循环后，S ＝7，i ＝6，满足条件；执行第二次循环后，S＝13，i ＝5，满足条件；执行第三次循环后，S ＝18，i ＝4，不满足条件，结束循环．故输出的i ＝4.【答案】 D3．根据如图所示的程序语句，可知输出的结果S 为________．【解析】 由程序可知，S ＝1，I ＝1，I ＜8；S ＝3，I ＝4，I ＜8；S ＝5，I ＝7，I ＜8；S＝7，I＝10，I＞8，此时结束循环，输出S＝7.【答案】74．写出求函数y＝x3＋3x2－24x＋30的值的算法语句，连续输入11个自变量的取值，输出相应的函数值．【解】解决本题的算法步骤：1．输入自变量x的值．2．计算y＝x3＋3x2－24x＋30.3．输出y.4．记录输入次数．5．判断输入的次数是否大于11.若是，则结束算法；否则，返回第一步．显然，可以用计数变量n(1≤n≤11)记录次数，通过循环结构来实现算法．算法框图如图：算法语句：n＝1Do输入xy＝x3＋3*x2-24*x+30输出yn=n+1Loop While n≤11。

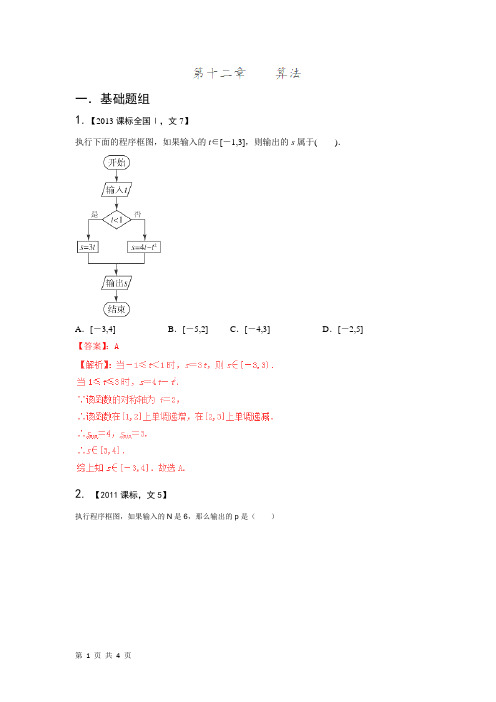
一．基础题组1.【2013课标全国Ⅰ，文7】执行下面的程序框图，如果输入的t∈[－1,3]，则输出的s属于()．A．[－3,4] B．[－5,2] C．[－4,3] D．[－2,5] 【答案】：A2.【2011课标，文5】执行程序框图，如果输入的N是6，那么输出的p是（）A. 120B.720C.1440D.5040【答案】B二．能力题组1.【2014全国1，文9】执行右面的程序框图，若输入的,,a b k分别为1,2,3，则输出的M ( )A.203B.72C.165D.158【答案】D2. 【2015高考新课标1，文9】执行右面的程序框图，如果输入的0.01t =，则输出的n =（ ）（A ） 5 （B ）6 （C ）10 （D ）12【答案】C【解析】执行第1次，t =0.01,S=1,n =0,m =12=0.5,S =S -m =0.5,2m m ==0.25,n =1,S =0.5＞t =0.01,是，循环，执行第2次，S =S -m =0.25,2m m ==0.125,n =2,S=0.25＞t =0.01,是，循环，执行第3次，S =S -m =0.125,2m m ==0.0625,n =3,S=0.125＞t =0.01,是，循环， 执行第4次，S=S-m =0.0625,2m m ==0.03125,n =4,S=0.0625＞t =0.01,是，循环， 执行第5次，S=S-m =0.03125,2m m ==0.015625,n =5,S=0.03125＞t =0.01,是，循环，执行第6次，S=S-m =0.015625,2m m ==0.0078125,n =6,S=0.015625＞t =0.01,是，循环， 执行第7次，S=S-m =0.0078125,2m m ==0.00390625,n=7,S=0.0078125＞t =0.01,否，输出n =7，故选C.考点：程序框图3.【2016新课标1文数】执行下面的程序框图，如果输入的0,1,x y ==n =1,则输出,x y 的值满足（A ）2y x = （B ）3y x = （C ）4y x = （D ）5y x =【答案】C【考点】程序框图与算法案例【名师点睛】程序框图基本是高考每年必考知识点,一般以客观题的形式出现,难度不大,求解此类问题只需按照程序逐步列出运行结果.。

2.1 算法的基本思想(建议用时：45分钟)[学业达标]一、选择题1．下列语句表达中，是算法的有( )①从泰安去看2014年巴西世界杯，可以先乘汽车到济南，再坐飞机抵达北京，再坐飞机抵达巴西；②利用公式S ＝12ah 计算底为1，高为2的三角形的面积； ③12x >2x ＋4； ④求M (1,2)与N (－3，－5)两点连线的方程，可先求MN 的斜率，再利用点斜式方程求得．A ．①②③B ．①③④C ．①②④D ．②③④【解析】 算法是解决问题的有效步骤，而③只是一个纯数学问题，无解决问题的步骤．【答案】 C2．已知直角三角形两直角边为a ，b ，求斜边长c 的一个算法分下列三步： ①计算c ＝a 2＋b 2；②输入直角三角形两直角边长a ，b 的值；③输出斜边长c 的值．其中正确的顺序是( )A ．①②③B ．②③①C ．①③②D ．②①③ 【解析】 要先有输入，再计算并输出，故顺序为②①③.【答案】 D3．关于一元二次方程x 2－5x ＋6＝0的求根问题，下列说法正确的是( )A ．只能设计一种算法B ．可以设计两种算法C ．不能设计算法D ．不能根据解题过程设计算法【解析】 一元二次方程的求解过程可以用公式法和因式分解法进行，可依据不同的解题过程来设计算法，故可以设计两种算法．【答案】 B4．算法：1．输入n .2．判断n 是否是2，若n ＝2，则n 满足条件；若n ＞2，则执行下一步．3．依次从2到n －1检验能不能整除n ，若不能整除n ，则n 满足条件．满足上述条件的n 是( )A ．素数B ．奇数C ．偶数D ．合数【解析】 由算法可知本算法的意义是n 除了1与它本身外，无其他约数，故此数是素数．【答案】 A5．在设计一个算法求12和14的最小公倍数中，设计的算法不恰当的一步是() A ．首先将12因式分解：12＝22×3B ．其次将14因式分解：14＝2×7C ．确定其公共素因数及其指数为22,31,71D ．其最小公倍数为S ＝2×3×7＝42【解析】 应为S ＝4×3×7＝84.【答案】 D二、填空题6．给出下列算法：1．输入x 的值；2．当x >4时，计算y ＝x ＋2；否则执行下一步；3．计算y ＝4－x ；4．输出y .当输入x ＝10时，输出y ＝________.【解析】 因为x ＝10>4.所以计算y ＝x ＋2＝12.【答案】 127．已知A (x 1，y 1)，B (x 2，y 2)，求直线AB 的斜率的一个算法如下：1．输入x 1，y 1，x 2，y 2的值；2．计算Δx ＝x 2－x 1，Δy ＝y 2－y 1；3．若Δx ＝0，则输出斜率不存在，否则(Δx ≠0)，k ＝____①____；4．输出斜率k .则①处应填________．【解析】 根据求斜率的公式知k ＝Δy Δx .所以①处应填ΔyΔx .【答案】 Δy Δx8．完成下面问题的算法：我国古代的一个著名算法案例：鸡兔49只，100条腿，求鸡兔的数量．算法如下：1．设有鸡x 只，兔y 只，则有⎩⎪⎨⎪⎧ x ＋y ＝49， ①2x ＋4y ＝100. ②2．将方程组中的第一个方程两边乘以－2加到第二个方程中去，得(4－2)y ＝100－49×2.解得y ＝1.3．________.【解析】 根据题意，求出y 的值后，应该再求x 的值，所以应填“将y ＝1代入①得x ＝48”．【答案】 将y ＝1代入①得x ＝48三、解答题9．写出过两点M (－2，－1)，N (2,3)的直线与坐标轴所围成区域的面积的一个算法．【解】 算法如下：1．取x 1＝－2，y 1＝－1，x 2＝2，y 2＝3；2．计算y －y 1y 2－y 1＝x －x 1x 2－x 1； 3．在第2步结果中令x ＝0得到y 的值m ，得直线与y 轴交点(0，m )；4．在第2步结果中令y ＝0得到x 的值n ，得直线与x 轴交点(n,0)；5．计算S ＝12|m |·|n |. 10．(1)设计一个算法，判断7是否为素数；(2)设计一个算法，判断35是否为素数．【解】 (1)算法步骤如下：1．用2除7.得到余数1.因为余数不为0，所以2不能整除7.2．用3除7，得到余数1.因为余数不为0，所以3不能整除7.3．用4除7，得到余数3.因为余数不为0，所以4不能整除7.4．用5除7，得到余数2.因为余数不为0，所以5不能整除7.5．用6除7，得到余数1.因为余数不为0，所以6不能整除7.因此，7是素数．(2)算法步骤如下：1．用2除35，得到余数1，因为余数不为0，所以2不能整除35.2．用3除35，得到余数2，因为余数不为0，所以3不能整除35.3．用4除35.得到余数3，因为余数不为0，所以4不能整除35.4．用5除35，得到余数0，因为余数为0，所以5能整除35.因此35不是素数．[能力提升]1．计算下列各式中S 的值，能设计算法求解的是( )①S ＝1＋12＋13＋…＋1100；②S ＝1＋2＋3＋…＋100＋…；③S ＝1＋2＋3＋…＋n (n ≥1，且n ∈N )．A ．①②B ．①③C ．②③D ．①②③【解析】 因为在②中没有控制项，无穷多项的和，没有结果，就没有算法．【答案】 B2．一个算法的步骤如下：1．输入x 的值；2．计算x 的绝对值y ；3．计算z ＝2y－y ；4．输出z 的值．如果输入x 的值为－3，则输出z 的值为( )A ．4B ．5C ．6D ．8 【解析】 分析算法中各变量、各语句的作用，再根据算法的步骤可知：该算法的作用是计算并输出z ＝2y －y 的函数值．当输入x 的值为－3时，算法步骤如下：1．输入x 的值为－3；2．计算x 的绝对值y ＝3；3．计算z ＝2y －y ＝23－3＝5；4．输出z 的值为5.故选B.【答案】 B3．已知一个算法如下：1．输入周长a 的值；2．计算边长l ＝a 3； 3．计算S ＝34×l 2； 4．输出S .该算法的功能是________；若等边三角形周长为12，则该三角形的面积为________．【解析】 依题设中的算法可知，该算法的功能是输入一个等边三角形的周长，输出该三角形的面积．当等边三角形的周长为12时，面积为4 3.【答案】 已知一个等边三角形的周长，求该三角形的面积 4 34．下面给出了解决问题的算法：1．输入x ；2．若x ≤1，则y ＝2x －1，否则y ＝x 2＋3；3．输出y .(1)这个算法解决的问题是________；(2)当输入的x 值为________时，输入值与输出值相等．【解析】 由算法的功能知，该算法为求分段函数y ＝⎩⎪⎨⎪⎧ 2x －x ，x 2＋x 的函数值．当x ≤1时，由2x －1＝x 得x ＝1，符合题意；当x >1时，由x 2＋3＝x 知x 无实根，不符合题意．综上知x ＝1.【答案】 (1)y ＝⎩⎪⎨⎪⎧ 2x －x x 2＋x (2)15．设计一个算法，求18 900,22 680和7 560的最大公因数．【解】 算法步骤：1．先将18 900进行素因数分解：18 900＝22×33×52×7；2．再将22 680进行素因数分解：22 680＝23×34×5×7；3．然后将7 560进行素因数分解：7 560＝23×33×5×7；4．确定它们的公共素因数：2,3,5,7；5．确定公共素因数的指数：公共素因数2,3,5,7的指数分别为2,3,1,1；6．最大公因数为22×33×5×7＝3 780.。

1.【2017河南省豫北名校联盟高三年级精英对抗赛，2】复数22iz i=-（i 为虚数单位）所对应的点位于复平面内（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限 【答案】B 【解析】22(2)42242(2)(2)555i i i i z i i i i +-====-+--+,对应的点24(,)55-位于第二象限，故选B.【要点回扣】复数的运算与复数的几何意义.2.【2017广东郴州市高三第二次教学质量监测试卷，1】已知,x y R ∈，i 是虚数单位.若x yi +与31ii++互为共轭复数，则x y +=（ ） A ．0 B ．1 C ．2 D ．3 【答案】D 【解析】3(3)(1)4221(1)(1)2i i i i i i i i ++--===-++-,所以31ii ++互为共轭复数为2i +，即2,1x y ==，所以3x y +=，故选D.【要点回扣】1.复数相关的概念；2.复数的运算.3.【河北唐山市2017届高三年级期末，2】i 是虚数单位，复数()z a i a R =+∈满足213z z i +=-，则z =（ ）A ．2或5 C D ．5 【答案】C【要点回扣】1、复数的运算；2、复数的模．4.在区间上随机选取一个数M ，不变执行如图所示的程序框图，且输入x 的值为1，然后输出的值为N ，则的概率为（ ）A ．51 B ．52C ．53D ．54【答案】C【解析】243013x x x -+≤⇒≤≤.这是一个循环结构，循环的结果依次为：2,1;3,2x n x n ====4,3x n ==.最后输出3.所以在区间上随机选取一个数M ，则1M ≤的概率为35p =，选C. 【要点回扣】程序框图.5．【2017广东湛江市高三上学期期中调研考试，7】若执行如图所示的框图，输入12341,2,4,8x x x x ====，则输出的结果等于（ ）A ．14 B ．74 C.154D ．4 【答案】C【解析】该程序框图所表示的算法功能为12481544x +++==，故选C.【要点回扣】程序框图．6.【2017河南省豫北名校联盟高三年级精英对抗赛,3】如果执行如图所示的程序框图，输入正整数(2)N N ≥和实数12N a a a ，，，，输出A B ，，则（ ）A ．AB +为12N a a a ，，，的和 B ．2A B+为12N a a a ，，，的算数平均数 C ．A 和B 分别是12N a a a ，，，中最大的数和最小的数 D ．A 和B 分别是12N a a a ，，，中最小的数和最大的数 【答案】C【解析】据程序框图可知，,A B 分别为12,,,N a a a 中的最大数和最小数，故选C. 【要点回扣】程序框图．7.用秦九韶算法求多项式765()765f x x x x =++ 432432x x x x ++++,当3x =时,3v 的值为 （ ）A.27B.86C. 262D.78 【答案】C【要点回扣】算法思想．8．【2017广东郴州市高三第二次教学质量监测试卷,5】考拉兹猜想又名31n +猜想，是指对于每一个正整数，如果它是奇数，则对它乘3再加1；如果它是偶数，则对它除以2.如此循环，最终都能得到1.阅读如图所示的程序框图，运行相应程序，输出的结果i =（ ）A ．4B ．5 C.6 D ．7 【答案】D【解析】模拟算法：开始：10,1a i ==，1a =不成立；a 是奇数，不成立，5,2a i ==，1a =不成立； a 是奇数，成立，16,3a i ==，1a =不成立； a 是奇数，不成立，8,4a i ==，1a =不成立； a 是奇数，不成立，4,5a i ==，1a =不成立； a 是奇数，不成立，2,6a i ==，1a =不成立； a 是奇数，不成立，1,7a i ==，1a =成立；输出7i =，结束算法.故选D. 【要点回扣】程序框图9.【2017河北唐山市高三年级期末,7】执行如图所示的程序框图，则输出的a = （ ）A ．1B ．1- C.4- D ．52- 【答案】C【要点回扣】程序框图10.设△ABC 的三边长分别为a 、b 、c ，△ABC 的面积为S ，内切圆半径为r ，则，类比这个结论可知：四面体S ﹣ABC 的四个面的面积分别为S 1、S 2、S 3、S 4，内切球半径为r ，四面体S ﹣ABC 的体积为V ，则r=（ ）A. B.C.D.【答案】C【解析】设四面体的内切球的球心为O ，则球心O 到四个面的距离都是R ，所以四面体的体积等于以O 为顶点，分别以四个面为底面的4个三棱锥体积的和．则四面体的体积为，∴R=．【要点回扣】类比推理．11．学生的语文、数学成绩均被评定为三个等级，依次为“优秀”“合格”“不合格”．若学生甲的语文、数学成绩都不低于学生乙，且其中至少有一门成绩高于乙，则称“学生甲比学生乙成绩好”．如果一组学生中没有哪位学生比另一位学生成绩好，并且不存在语文成绩相同、数学成绩也相同的两位学生，则这一组学生最多有（ ） A.2人 B.3人 C.4人 D.5人 【答案】B【解析】用ABC 分别表示优秀、及格和不及格，显然语文成绩得A 的学生最多只有1个，语文成绩得B 得也最多只有一个，得C 最多只有一个，因此学生最多只有3人，显然（AC ）（BB ）（CA ）满足条件，故学生最多有3个．故选：B ． 【要点回扣】合情推理．12．【2017广西南宁、梧州高三毕业班摸底联考，11】给出定义：设()'f x 是函数()y f x =的导函数，()''f x 是函数()'f x 的导函数，若方程()''0f x =有实数解0x ，则称点()()00 x f x ，为函数()y f x =的“拐点”.已知函数()34sin cos f x x x x =+-的拐点是()()00 M x f x ，，则点M （ ）A ．在直线3y x =-上B ．在直线3y x =上 C.在直线4y x =-上 D ．在直线4y x =上 【答案】B【解析】()()00'34cos sin ''4sin cos 0 4sin cos 0f x x x f x x x x x =++=-+=-=，，，所以()003f x x =，故()()00 M x f x ，在直线3y x =上.故应选B. 【要点回扣】新定义13.某同学在纸上画出如下若干个三角形：△▲△△▲△△△▲△△△△▲△△△△△▲……若依此规律，得到一系列的三角形，则在前2015个三角形中共有▲的个数是（ ） A ．64 B ．63 C ．62 D ．61【答案】C【解析】前n 个三角形中共有▲的个数是123n n ⋯＋＋＋＋＋＝(3)2n n +，由(3)2n n +2015＝解得62n ＝。

单元滚动检测三导数及其应用考生注意：1．本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，共4页．2．答卷前，考生务必用蓝、黑色字迹的钢笔或圆珠笔将自己的姓名、班级、学号填写在相应位置上．3．本次考试时间120分钟，满分150分．4．请在密封线内作答，保持试卷清洁完整．第Ⅰ卷(选择题共60分)一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．(2016·北京朝阳区模拟)曲线f(x)＝x ln x在点(1，f(1))处的切线的倾斜角为()A.π6 B.π4C.π3 D.π22．(2016·福建三明一中月考)已知函数f(x)的导函数为f′(x)，且满足f(x)＝2x·f′(1)＋1n x，则f′(1)等于()A．－e B．－1 C．1 D．e3．(2016·赣州第二中学模拟)已知函数f(x)＝x2－5x＋2ln x，则函数f(x)的单调递增区间是()A．(0，12)和(1，＋∞)B．(0,1)和(2，＋∞)C．(0，12)和(2，＋∞)D．(1,2)4．已知f(x)的定义域为(0，＋∞)，f′(x)为f(x)的导函数且满足f(x)＜－xf′(x)，则不等式(x＋1)f(x＋1)＞f(x2－1)·f(x2－1)的解集是()A．(0,1) B．(1，＋∞)C．(1,2) D．(2，＋∞)5．函数y＝x－2sin x，x∈－π2，π2]的大致图像是()6．若函数y ＝cos x ＋ax 在－π2，π2]上是增函数，则实数a 的取值范围是( ) A ．(－∞，－1] B ．(－∞，1] C ．－1，＋∞)D ．1，＋∞)7．函数f (x )＝x 3－3ax －a 在(0,1)内有最小值，则a 的取值范围为( ) A ．0≤a ＜1 B ．0＜a ＜1 C ．－1＜a ＜1D ．0＜a ＜128．(2016·山师大附属中学高三上学期模拟)设函数f (x )＝e x －e －x －2x ，下列结论正确的是( ) A ．f (2x )min ＝f (0) B ．f (2x )max ＝f (0)C ．f (2x )在(－∞，＋∞)上是减少的，无极值D ．f (2x )在(－∞，＋∞)上是增加的，无极值9．(2016·长沙一模)若函数f (x )＝x ＋b x (b ∈R )的导函数在区间(1,2)上有零点，则f (x )在下列区间上是增加的是( ) A ．(－2,0) B ．(0,1) C ．(1，＋∞)D ．(－∞，－2)10．(2016·许昌模拟)已知y ＝f (x )为(0，＋∞)上的可导函数，且有f ′(x )＋f (x )x ＞0，则对于任意的a ，b ∈(0，＋∞)，当a ＞b 时，有( ) A ．af (a )＜bf (b ) B ．af (a )＞bf (b ) C ．af (b )＞bf (a )D ．af (b )＜bf (a )11．已知函数f (x )＝x 3＋3x 2－9x ＋1，若f (x )在区间k,2]上的最大值为28，则实数k 的取值范围为( ) A ．－3，＋∞) B ．(－3，＋∞) C ．(－∞，－3)D ．(－∞，－3]12．(2016·兰州高三实战考试)已知二次函数f (x )＝ax 2＋bx ＋c 的导数为f ′(x )，f ′(0)>0，对于任意的实数x 都有f (x )≥0，则f (1)f ′(0)的取值范围是( )A ．32，＋∞) B ．2，＋∞) C ．52，＋∞)D ．3，＋∞)第Ⅱ卷(非选择题 共90分)二、填空题(本大题共4小题，每小题5分，共20分．把答案填在题中横线上) 13．若函数f (x )＝ln x ＋ax 的图像上存在与直线2x －y ＝0平行的切线，则实数a 的取值范围为________．14．若函数f (x )＝sin x ＋ax 为R 上的减函数，则实数a 的取值范围是________． 15．已知函数f (x )＝1n x －a ，若f (x )＜x 2在(1，＋∞)上恒成立，则实数a 的取值范围是________．16．已知f (x )＝ln x －x 4＋34x ，g (x )＝－x 2－2ax ＋4，若对任意的x 1∈(0,2]，存在x 2∈1,2]，使得f (x 1)≥g (x 2)成立，则a 的取值范围是________．三、解答题(本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤)17.(10分)已知函数f (x )＝x 3－4x 2＋5x －4. (1)求曲线f (x )在点(2，f (2))处的切线方程； (2)求经过点A (2，－2)的曲线f (x )的切线方程.18.(12分)已知函数f (x )＝ln x ＋ke x (k 为常数)，曲线y ＝f (x )在点(1，f (1))处的切线与x 轴平行.(1)求实数k 的值； (2)求函数f (x )的单调区间.19.(12分)(2016·南昌模拟)已知函数f(x)＝12x2－(a＋1)x＋a ln x(a∈R).(1)若f(x)在(2，＋∞)上是增加的，求a的取值范围；(2)若f(x)在(0，e)内有极小值12，求a的值.20.(12分)设函数f(x)＝x3＋bx2＋cx＋d(x∈R)，已知F(x)＝f(x)－f′(x)是奇函数，且F(1)＝－11.(1)求b，c，d的值；(2)求F(x)的单调区间与极值.21.(12分)已知函数f(x)＝e x－1，g(x)＝x＋x，其中e是自然对数的底数，e＝2.718 28….(1)证明：函数h(x)＝f(x)－g(x)在区间(1,2)上有零点；(2)求方程f(x)＝g(x)的根的个数，并说明理由.22.(12分)已知f(x)＝a ln x＋12x2－x(a∈R).(1)若x＝2是函数f(x)的一个极值点，求f(x)的最小值；(2)对任意x∈(e，＋∞)，f(x)－ax＞0恒成立，求a的取值范围.答案解析1．B∵f′(x)＝ln x＋1，∴f′(1)＝1，又∵直线倾斜角的取值范围是0，π)．∴f(x)在(1，f(1))处的切线的倾斜角为π4.]2．B因为f(x)＝2xf′(1)＋1n x，所以f′(x)＝2f′(1)＋1 x，令x＝1，得f′(1)＝2f′(1)＋1，解得f′(1)＝－1.故选B.] 3．C函数f(x)＝x2－5x＋2ln x的定义域是(0，＋∞)，令f′(x)＝2x－5＋2x＝2x2－5x＋2x＝(x－2)(2x－1)x＞0，解得0＜x＜12或x＞2，故函数f(x)的单调递增区间是(0，12)，(2，＋∞)．]4．D因为f(x)＋xf′(x)＜0，所以xf(x)]′＜0，故xf(x)在(0，＋∞)上为单调递减函数，又(x＋1)f(x＋1)＞(x2－1)·f(x2－1)，所以x＋1＜x2－1，解得x＞2.]5．D因为函数为奇函数，所以图像关于原点对称，排除A，B.函数的导数为f′(x)＝1－2cos x，由f′(x)＝1－2cos x＝0，得cos x＝1 2，又x∈－π2，π2]，所以x＝±π3.当0＜x＜π3或－π3＜x＜0时，f′(x)＜0，函数是减少的，当π3＜x＜π2或－π2＜x＜－π3时，f′(x)＞0，函数是增加的，所以当x＝π3时，函数取得极小值，当x＝－π3时，函数取得极大值．故选D.]6．D y′＝－sin x＋a，若函数在－π2，π2]上是增函数，则a≥sin x在－π2，π2]上恒成立，所以a≥1，即实数a的取值范围是1，＋∞)．]7．B∵y′＝3x2－3a，令y′＝0，可得a＝x2. 又∵x∈(0,1)，∴0＜a＜1.故选B.]8．D∵f(2x)＝e2x－e－2x－4x，∴f′(2x)＝2e2x＋2e－2x－4≥4e2x·e－2x－4＝0，f(2x)在(－∞，＋∞)上是增加的，无极值．]9．D由题意知f′(x)＝1－bx2，∵函数f(x)＝x＋bx(b∈R)的导函数在区间(1,2)上有零点，∴当1－bx2＝0时，b＝x2，又x∈(1,2)，∴b∈(1,4)．令f′(x)＞0，解得x＜－b或x＞b，即f(x)的单调递增区间为(－∞，－b)，(b，＋∞)，∵b∈(1,4)，∴(－∞，－2)符合题意，故选D.]10．B f′(x)＋f(x)x＞0⇒xf′(x)＋f(x)x＞0⇒[xf(x)]′x＞0，即xf(x)]′x＞0.∵x＞0，∴xf(x)]′＞0，即函数y＝xf(x)为增函数，由a，b∈(0，＋∞)且a＞b，得af(a)＞bf(b)，故选B.]11．D由题意知f′(x)＝3x2＋6x－9，令f′(x)＝0，解得x＝1或x＝－3，所以f′(x)，f(x)随x的变化情况如下表：又f(－3)＝28，f(1)＝－4，f(2)＝3，f(x)在区间k,2]上的最大值为28，所以k≤－3.] 12．B由题意得，f′(x)＝2ax＋b，∵f′(0)>0，∴b>0，又∵任意x∈R，都有f(x)≥0，∴a>0，∴Δ＝b2－4ac≤0⇔ac≥b24⇒acb2≥14⇒ab·cb≥14，∴c>0.∴f(1)f′(0)＝a＋b＋cb＝1＋ab＋cb≥1＋2 a b ·c b ≥1＋214＝2， 当且仅当a b ＝c b ＝12⇒a ＝c ＝12b >0时，等号成立， ∴f (1)f ′(0)的取值范围是2，＋∞)，故选B.] 13．(－∞，2)解析 函数f (x )＝ln x ＋ax 的图像上存在与直线2x －y ＝0平行的切线，即f ′(x )＝2在(0，＋∞)上有解，又f ′(x )＝1x ＋a ，即1x ＋a ＝2在(0，＋∞)上有解，即a ＝2－1x 在(0，＋∞)上有解，因为x ＞0，所以2－1x ＜2，所以实数a 的取值范围是(－∞，2)． 14．(－∞，－1]解析 ∵f ′(x )＝cos x ＋a ，由题意可知，f ′(x )≤0对任意的x ∈R 都成立， ∴a ≤－1，故实数a 的取值范围是(－∞，－1]． 15．－1，＋∞)解析 ∵函数f (x )＝ln x －a ，且f (x )＜x 2在(1，＋∞)上恒成立， ∴函数f (x )＝ln x －a ＜x 2在(1，＋∞)上恒成立， ∴a ＞ln x －x 2，令h (x )＝ln x －x 2，有h ′(x )＝1x －2x ， ∵x ＞1， ∴1x －2x ＜0，∴h (x )在(1，＋∞)上为减函数， ∴当x ∈(1，＋∞)时，h (x )＜h (1)＝－1， ∴a ≥－1. 16．54，＋∞)解析 因为f ′(x )＝1x －34×1x 2－14＝－x 2＋4x －34x 2＝－(x －1)(x －3)4x 2，易知，当x ∈(0,1)时，f ′(x )＜0，当x ∈(1,2]时，f ′(x )＞0，所以f (x )在(0,1)上是减少的， 在(1,2]上是增加的，故f (x )min ＝f (1)＝12.对于二次函数g (x )＝－x 2－2ax ＋4，易知该函数开口向下， 所以其在区间1,2]上的最小值在端点处取得， 即g (x )min ＝min {}g (1)，g (2).要使对任意的x 1∈(0,2]，存在x 2∈1,2]， 使得f (x 1)≥g (x 2)成立，只需f (x 1)min ≥g (x 2)min ， 即12≥g (1)且12≥g (2)，所以12≥－1－2a ＋4且12≥－4－4a ＋4，解得a ≥54.17．解 (1)∵f ′(x )＝3x 2－8x ＋5，∴f ′(2)＝1，又f (2)＝－2， ∴曲线在点(2，f (2))处的切线方程为y ＋2＝x －2，即x －y －4＝0.(2)设曲线与经过点A (2，－2)的切线相切于点P (x 0，x 30－4x 20＋5x 0－4)． ∵f ′(x 0)＝3x 20－8x 0＋5，∴切线方程为y －(－2)＝(3x 20－8x 0＋5)(x －2)，又切线过点P (x 0，x 30－4x 20＋5x 0－4)， ∴x 30－4x 20＋5x 0－2＝(3x 20－8x 0＋5)·(x 0－2)， 整理得(x 0－2)2(x 0－1)＝0， 解得x 0＝2或x 0＝1，∴经过A (2，－2)的曲线f (x )的切线方程为x －y －4＝0 或y ＋2＝0.18．解 (1)x ＞0，f ′(x )＝1x －ln x －ke x.又由题知f ′(1)＝1－ke ＝0，所以k ＝1.(2)x ＞0，f ′(x )＝1x －ln x －1e x.设h (x )＝1x －ln x －1(x ＞0)，则h ′(x )＝－1x 2－1x ＜0， 所以h (x )在(0，＋∞)上是减少的．由h (1)＝0知，当0＜x ＜1时，h (x )＞0，所以f ′(x )＞0； 当x ＞1时，h (x )＜0，所以f ′(x )＜0.综上，f (x )的单调增区间是(0,1)，单调减区间是(1，＋∞)． 19．解 (1)∵f (x )在(2，＋∞)上是增加的，∴f ′(x )＝x 2－(a ＋1)x ＋ax ≥0在(2，＋∞)上恒成立，即x 2－(a ＋1)x ＋a ≥0在(2，＋∞)上恒成立， 即(1－x )a ＋x 2－x ≥0在(2，＋∞)上恒成立， 即(1－x )a ≥x －x 2在(2，＋∞)上恒成立， 即a ≤x 在(2，＋∞)上恒成立． ∴实数a 的取值范围是(－∞，2]． (2)f (x )的定义域为(0，＋∞)， f ′(x )＝x 2－(a ＋1)x ＋a x ＝(x －a )(x －1)x .①当a ＞1时，令f ′(x )＞0，结合f (x )定义域解得0＜x ＜1或x ＞a ，∴f (x )在(0,1)和(a ，＋∞)上是增加的，在(1，a )上是减少的， 此时f (x )极小值＝f (a )＝－12a 2－a ＋a ln a ，若f (x )在(0，e)内有极小值12，则1＜a ＜e ，但此时－12a 2－a ＋a ln a ＜0与f (x )＝12矛盾．②当a ＝1时，此时f ′(x )恒大于等于0，不可能有极小值． ③当a ＜1时，不论a 是否大于0，f (x )的极小值只能是 f (1)＝－12－a ，令 －12－a ＝12，即a ＝－1，满足a ＜1. 综上所述，a ＝－1.20．解 因为f (x )＝x 3＋bx 2＋cx ＋d ， 所以f ′(x )＝3x 2＋2bx ＋c .从而F (x )＝x 3＋bx 2＋cx ＋d －(3x 2＋2bx ＋c ) ＝x 3＋(b －3)x 2＋(c －2b )x ＋(d －c )，由F (x )是一个奇函数，所以F (0)＝0，F (－x )＝－F (x )， 得d －c ＝0，b －3＝0，故b ＝3，d ＝c .又由F (1)＝－11可得1＋(b －3)＋(c －2b )＋(d －c )＝－11， 即b －d ＝9，所以d ＝c ＝－6.(2)由(1)知F (x )＝x 3－12x ，从而F ′(x )＝3x 2－12， 令3x 2－12＝0，得x ＝±2，由F ′(x )＝3x 2－12＞0，得x ＞2或x ＜－2， 由F ′(x )＝3x 2－12＜0，得－2＜x ＜2.故(－∞，－2)和(2，＋∞)是函数F (x )的单调递增区间， (－2,2)是函数F (x )的单调递减区间． F (x )在x ＝－2时取得极大值，极大值为16， F (x )在x ＝2时取得极小值，极小值为－16.21．(1)证明 由h (x )＝f (x )－g (x )＝e x －1－x －x ，得 h (1)＝e －3＜0，h (2)＝e 2－3－2＞0，h (1)·h (2)＜0， 所以函数h (x )在区间(1,2)上有零点． (2)解 由(1)，得h (x )＝e x －1－x －x .由g (x )＝x ＋x ，知x ∈0，＋∞)，而h (0)＝0，则x ＝0为h (x )的一个零点，而h (x )在(1,2)内有零点，因此h (x )在0，＋∞)上至少有两个零点．因为h ′(x )＝e x －12x －12－1，记φ(x )＝e x －12x －12－1，则φ′(x )＝e x ＋14x －32.当x ∈(0，＋∞)时，φ′(x )＞0，因此φ(x )在(0，＋∞)上是增加的，则φ(x )在(0，＋∞)内至多只有一个零点，又h (0)＝0，所以h (x )在0，＋∞)内有两个零点．所以方程f (x )＝g (x )的根的个数为2. 22．解 (1)f ′(x )＝ax ＋x －1. 由f ′(2)＝0，得a ＝－2，此时f ′(x )＝－2x ＋x －1＝x 2－x －2x ，可知，f (x )在(0,2)上是减少的，在(2，＋∞)上是增加的，所以f (x )min ＝f (2)＝－2ln 2.(2)由f (x )－ax ＝a ln x ＋12x 2－x －ax ＞0在(e ，＋∞)内恒成立， 又因为x ∈(e ，＋∞)，所以x －ln x ＞0，因而a ＜12x 2－xx －ln x.设g (x )＝12x 2－xx －ln x，x ∈(e ，＋∞)．因为g ′(x )＝(x －1)(x －ln x )－(1－1x )(12x 2－x )(x －ln x )2＝(x －1)(12x ＋1－ln x )(x －ln x )2，当x ∈(e ，＋∞)时，x －1＞0，令r(x)＝12x＋1－ln x，则r′(x)＝12－1x(x＞e)，所以r′(x)＞0，所以r(x)在(e，＋∞)上是增加的，所以对任意x∈(e，＋∞)，r(x)＞r(e)＝e2＞0.所以g′(x)＞0，所以g(x)在(e，＋∞)上为增函数，所以a≤g(e)＝e2－2e 2(e－1).。

备战2018高考数二轮专题精炼：函数与方程1、设是定义在R上的偶函数，对任意的，都有，且当时，，若在区间内关于的方程恰有三个不同的实数根，则实数的取值范围是A. B. C. D.【答案】C【解析】因为是定义在R上的偶函数,所以,又，所以函数关于x=2轴对称,即,,函数的周期为4,且当时，，分别画出y=f(x)和g(x)=的图象,使其恰有三个交点,则需满足,即,解得,故选C.2、已知，则方程所有实数根的个数为A. B. C. D.【答案】D【解析】在同一坐标系内作出函数的图象，如图所示，根据函数图象可知，两函数的图象交点的个数为5个，所以方程所有实数根的个数为5个。

选D．3、设函数,若关于的方程恰好有六个不同的实数解,则实数的取值范围为（）A. B. C. D.【答案】B【解析】作出函数的图象如图，令，则方程化为，要使关于的方程，恰好有六个不同的实数根，则方程在内有两个不同实数根，，解得实数的取值范围是，故选B.4、已知定义在上的偶函数满足，且当时，，若在内关于的方程恰有3个不同的实数根，则的取值范围是（）A. B. C. D.【答案】C【解析】∵,∴，即，∴ 函数f(x)的周期为4。

当x∈[0,2]时，则？x∈[？2,0]，∴，∵f(x)是偶函数，∴由f(x)？loga(x+2)=0，得f(x)=loga(x+2)，令作出函数的图象如图所示：①当0<a<1时，函数g(x)=loga(x+2)单调递减，此时两函数的图象只有1个交点，不满足条件；②当a>1时，要使方程f(x)？loga(x+2)=0恰有3个不同的实数根，则需函数f(x)与g(x)=loga(x+2)的图象有3个不同的交点，则需满足，即，解得。

故a的取值范围是。

答案：C5、已知偶函数满足，且当时，，则关于的方程在上根的个数是（）A. 10个B. 8个C. 6个D. 4个【答案】C【解析】∵∴∴函数的周期为2在上，画出函数与的简图，如图所示：根据图象，关于的方程在上根的个数是6个，故选C6、若方程有两个不等的实数根，则的取值范围是（）A. B. C. D.【答案】C【解析】由方程得：，因为的最低点为，当过时有一个交点，此时，所以要让方程两个不等实数根，只需，故选C.7、已知函数，若函数在上有两个零点，则实数的取值范围是（）A. B. C. D.【答案】B【解析】由解析式可得函数的第一部分为指数函数的一部分，且随着a的变化而上下平移，右半部分为直线的一部分，且是固定的，作图如下：结合图象分析可得，当左半部分的图象介于两红线之间时符合题意，而红线与y轴的焦点坐标为1-a，且只需0≤1-a＜1，即即可故选B。

第十一章 算法初步题型132 条件分支结构型算法问题2014年1.（2014四川文6）执行如图所示的程序框图，如果输入的,x y ∈R ，那么输出的S 的最大值为（ ）.A.0B.1C.2D.32015年1.（2015福建文4）阅读如图所示的程序框图，运行相应的程序．若输入x 的值为1，则输出y 的值为（ ）.A ．2 B.7 C.8 D ．1281. 解析 由题意得，该程序表示分段函数2,29,2x x y x x ⎧=⎨-<⎩…，则()1918f =-=.故选C ．2017年1.（2017山东卷文6）执行右侧的程序框图，当输入的x 的值为4时，输出的y 的值为2，则空白判断框中的条件可能为（ ）. A.3?x > B.4?x > C.4?x …输入x 结束输出y x ≥2?结束S S开始开始结束结束开始2 ?D. 5?x …1. 解析 解法一：易知4x =不满足判断框中的条件，只有选项B 符合.故选B.解法二：输入x 为4，要想输出y 为2，则程序经过2log 42y ==，故判断框内填4x >.故选B.2.（2017江苏卷17）如图所示是一个算法流程图，若输入x 的值为116，则输出y = ．2.解析 由1116x =<，得42212log 2log 2216y -=+=+=-．题型133 循环结构型算法问题2013年1. (2013安徽文3）如图所示，程序据图（算法流程图）的输出结果为（ ）.A. 34 B. 16 C. 1112D.25242. (2013天津文3） 阅读右边的程序框图， 运行相应的程序， 则输出n = ( ).A.7B. 6C.5D. 43．(2013广东文5）执行如图1所示的程序框图，若输入n 的值为3，则输入s =（ ）.a 1 ?开始结束结束开始A ．1B ．2C ．4D ．75. （2013山东文6）执行两次右图所示的程序框图，若第一次输入的a 的值为 1.2-，第二次输入的a 的值为1.2，则第一次，第二次输出的a 的值分别为（ ）.A. 0.2,0.2B.0.2,0.8C. 0.8,0.2D. 0.8,0.86．(2013福建文8） 阅读如图所示的程序框图，运行相应的程序，如果输入某个正整数n 后，输出的()10,20S ∈，那么n 的值为（ ）. A ．3 B.4 C.5 D.67. (2013辽宁文8）执行如图所示的程序框图，若输入的8n =，则输出的S =（ ）.A. 49B. 67C. 89D. 1011B = B i开始结束开始结束结束开始8. (2013重庆文5）执行如图所示的程序框图，则输出的k 的值是（ ） A. 3 B. 4 C. 5 D. 69. (2013湖南文12）执行如图1所示的程序框图，如果输入1,2,a b ==则输出a的值为 .10．（2013湖北文13）阅读如图所示的程序框图，运行相应的程序. 若输入m 的值为2，则输出的结果i = ．11. (2013浙江14）某程序框图如图所示，则该程序运行后输出的S = _________.2014年 1. （2014安徽文4）如图所示，程序框图（算法流程图）的输出结果是（ ）. A.34 B.55 C.78 D.89。

2.3.1 条件语句(建议用时：45分钟)[学业达标]一、选择题1．给出下列四个问题：①输入一个数x ，输出它的绝对值；②求函数f (x )＝⎩⎪⎨⎪⎧ x 2－1，x ≥0，x ＋2，x <0的函数值；③求面积为6的正方形的周长；④求三个数a ，b ，c 中的最大数．其中需要用条件语句来描述其算法的个数是( )A ．1B ．2C ．3D ．4【解析】 其中①②④对输入的数均需进行判断，需要条件语句．【答案】 C2．当a ＝1，b ＝3时，执行完下面一段程序后，x 的值是( ) 输入a ，b ；If a >b Thenx ＝a ＋bElse x ＝a －bEnd If输出x .A ．1B ．3C ．4D ．－2【解析】 由算法语句可知a <b ，x ＝a －b ＝－2.【答案】 D3．当a ＝3时，下面的程序输出的结果是( )输入a ；If a <0 Theny ＝2＋aElsey ＝3*aEnd If输出y.C．10 D．5【解析】当a＝3时，3>0.则y＝3×3＝9.【答案】 A4．为了在运行下面的程序之后输出y＝9，键盘输入应该是( ) 输入x；If x<0 Theny＝(x＋1)*(x＋1)Elsey＝(x－1)*(x－1)End If输出y.A．x＝－4B．x＝－2C．x＝4或x＝－4D．x＝2或－2【解析】当x<0时，由(x＋1)2＝9，得x＝－4.当x≥0时，由(x－1)2＝9，得x＝4.【答案】C5．输入x；If x<4 T heny＝xElseIf x<10 T heny＝2*x-6Elsey＝3* x-12End IfEnd If输出y.如果输入12，则输出结果为( )A．12 B．18【解析】因为x＝12,12>4且12>10，所以y＝3×12－12＝24.【答案】 D二、填空题6．下列程序的功能是：判断任意输入的数x是否是正数，若是，输出它的平方值；若不是，输出它的相反数．输入x；If ________T heny＝－xElsey＝x*xEnd If输出y.则填入的条件应该是________．【解析】由程序的功能和If语句可知，If后面的条件应填x≤0.【答案】x≤07．阅读下列程序，回答问题：输入x1，x2；If x1＝x2Theny＝x1－x2Elsey＝x1＋x2End If输出y.如果输入x1＝3，x2＝5，那么执行此算法的输出结果是________．【解析】x1＝3，x2＝5，x1≠x2，所以y＝3＋5＝8.【答案】88．执行下面的程序语句，如果输入的t∈[－1,3]，则输出的s属于________.输入t；If t>1 Thens＝3*tElses＝4*t+t2End If输出s【解析】 由题意知：s ＝⎩⎪⎨⎪⎧ 3t ，t >1，4t －t 2，t ≤1.当t ∈[－1,1]时，s ＝4t －t 2＝－(t －2)2＋4∈[－5,3]，当t ∈(1,3]时，s ＝3t ∈(3,9]．所以s ∈[－5,9]．【答案】 [－5,9]三、解答题9．设计计算y ＝⎩⎪⎨⎪⎧ x ＋x ，x 2＋x 函数值的算法，并用相应的算法语句加以描述．【解】 算法如下：1．输入x .2．如果x ≥0，则y ＝x ＋2；否则，执行第3步．3．y ＝x 2＋2.4．输出y .用算法语句描述为：输入x ；If x ＞＝0 Theny ＝x ＋2Elsey ＝x *x ＋2End If输出y .10．已知某商店对顾客购买货款数满500元，减价3%，不足500元不予优惠，输入一顾客购物的货款数，计算出这个顾客实交的货款，画出相应程序框图，并写出程序．【解】 设购物的货款数为x 元，则顾客实际应交的货款y 元为y ＝⎩⎪⎨⎪⎧ x －，x ≥500，x ，x ＜500，即y ＝⎩⎪⎨⎪⎧ 0.97x ，x ≥500，x ，x ＜500. 所以，程序框图如图所示：算法程序如下：[能力提升]1．阅读下列语句：输入a ；If a >5 Thenb ＝2*aElseb ＝a *a ＋1End If输出b .如果输出5，则输入的a 为( )A ．2.5B ．2C ．－2D ．±2【解析】 由算法语句可知，令2a ＝5，则a ＝52<5(舍)．令a 2＋1＝5， 则a ＝±2，满足题意．【答案】 D2．以下程序运行的结果为( )输入a ＝2b ＝－2m ＝ab＝mIf a>b Thenx＝a－bElsex＝a＋bEnd If输出x.A．0 B．2C．4 D．－4【解析】运行过程中，m＝2，a＝－2，b＝2，因为a≤b，所以x＝a＋b＝0.【答案】 A3．已知算法语句如下，则f(－3)＋f(2)＝________.输入x；If x＜＝0 Thenf(x)＝x－1Elsef(x)＝2xEnd If输出f(x)．【解析】由算法语句可知，当x≤0时，f(x)＝x－1，当x>0时，f(x)＝2x，所以f(－3)＝－3－1＝－4，f(2)＝22＝4，所以f(－3)＋f(2)＝0.【答案】04．给出如下程序(其中x满足0<x<12)输入x；If x>0 And x＜＝4 Theny＝2* xElseIf x≤8Theny＝8Elsey＝24－2* xEnd IfEnd If(1)该程序的功能是求什么函数的函数值；(2)画出这个程序的算法框图．【解】 (1)函数的关系式为y ＝⎩⎪⎨⎪⎧ 2x x ，x ，24－2x x(2)。

课时分层训练(四十八) 算法与算法框图A 组 基础达标(建议用时：30分钟)一、选择题1．执行如图9-1-14所示的算法框图，若输入的实数x ＝4，则输出结果为( )图9-1-14A ．4B ．3C ．2D ．14C [依题意，输出的y ＝log 24＝2.]2．(2017·天津河西区调研)阅读算法框图9-1-15，运行相应的程序，则输出S 的值为( )【导学号：66482432】图9-1-15A．－10 B．6C．14 D．18B[初始值S＝20，i＝1.执行一次循环，i＝2，S＝20－2＝18；执行两次循环，i＝2×2＝4，S＝18－4＝14；执行三次循环，i＝2×4＝8，S＝14－8＝6满足i＞5，终止循环，输出S＝6.]3．(2016·四川高考)秦九韶是我国南宋时期的数学家，普州(现四川省安岳县)人，他在所著的《数书九章》中提出的多项式求值的秦九韶算法，至今仍是比较先进的算法．如图9-1-16所示的算法框图给出了利用秦九韶算法求某多项式值的一个实例，若输入n，x的值分别为3,2，则输出v的值为()图9-1-16A．35 B．20C．18 D．9C[由算法框图知，初始值：n＝3，x＝2，v＝1，i＝2，第一次：v＝4，i＝1；第二次：v＝9，i＝0；第三次：v＝18，i＝－1.i ＝－1<0，结束循环，输出v ＝18，故选C.]4．(2016·郑州模拟)随机抽取某产品n 件，测得其长度分别是a 1，a 2，…，a n ，如图9-1-17所示的算法框图输出样本的平均值为s ，则在处理框①中应填入的式子是( )图9-1-17A ．s ＝s ＋a i iB ．s ＝is ＋a i i ＋1C ．s ＝s ＋a iD ．s ＝(i －1)s ＋a i iD [设a 1＋a 2＋…＋a i ＝S i ，则在第i －1次时S i －1＝(i －1)s ，在第i 次时S i＝S i －1＋a i ，∴s ＝S i i ＝S i －1＋a i i ＝(i －1)s ＋a i i，故选D.] 5．(2016·天津高考)阅读下边的算法框图，运行相应的程序，则输出S 的值为( )图9-1-18A．2 B．4C．6 D．8B[S＝4不满足S≥6，S＝2S＝2×4＝8，n＝1＋1＝2；n＝2不满足n>3，S＝8满足S≥6，则S＝8－6＝2，n＝2＋1＝3；n＝3不满足n>3，S＝2不满足S≥6，则S＝2S＝2×2＝4，n＝3＋1＝4；n＝4满足n>3，输出S＝4.故选B.]6．(2015·全国卷Ⅱ)下边算法框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”．执行该算法框图，若输入的a，b分别为14,18，则输出的a＝()图9-1-19A．0 B．2C．4 D．14B[a＝14，b＝18.第一次循环：14≠18且14<18，b＝18－14＝4；第二次循环：14≠4且14>4，a＝14－4＝10；第三次循环：10≠4且10>4，a＝10－4＝6；第四次循环：6≠4且6>4，a＝6－4＝2；第五次循环：2≠4且2<4，b＝4－2＝2；第六次循环：a＝b＝2，跳出循环，输出a＝2，故选B.]二、填空题7．(2017·江南名校联考)某算法框图9-1-20如图所示，判断框内为“k≥n”，n为正整数，若输出的S＝26，则判断框内的n＝________.【导学号：66482433】图9-1-204[依题意，执行题中的算法框图，进行第一次循环时，k＝1＋1＝2，S＝2×1＋2＝4；进行第二次循环时，k＝2＋1＝3，S＝2×4＋3＝11；进行第三次循环时，k＝3＋1＝4，S＝2×11＋4＝26.因此当输出的S＝26时，判断框内的条件n＝4.]8．执行如图9-1-21所示的算法框图(算法流程图)，输出的n为________．图9-1-214[执行第一次判断：|a－1.414|＝0.414＞0.005，a＝32，n＝2；执行第二次判断：|a－1.414|＝0.086＞0.005，a＝75，n＝3；执行第三次判断：|a－1.414|＝0.014＞0.005，a＝1712，n＝4；执行第四次判断：|a－1.414|＜0.005，输出n＝4.]9．执行下边的程序，输出的结果是________．11[根据循环结构可得：第一次，S＝1×3＝3，i＝3＋2＝5，由于3≤200，则循环；第二次：S＝3×5＝15，i＝5＋2＝7，由于15≤200，则循环；第三次：S＝15×7＝105，i＝7＋2＝9，由于105≤200，则循环；第四次：S＝105×9＝945，i＝9＋2＝11，由于945＞200，则循环结束，故此时输出i＝11.]10．(2017·石家庄质检)执行如图9-1-22所示的算法框图，如果输入的t＝50，则输出的n＝________.图9-1-226[第一次运行后S＝2，a＝3，n＝1；第二次运行后S＝5，a＝5，n＝2；第三次运行后S＝10，a＝9，n＝3；第四次运行后S＝19，a＝17，n＝4；第五次运行后S＝36，a＝33，n＝5；第六次运行后S＝69，a＝65，n＝6，此时不满足S＜t，退出循环，输出n＝6.]B组能力提升(建议用时：15分钟)1．(2016·全国卷Ⅲ)执行下面的算法框图，如果输入的a＝4，b＝6，那么输出的n＝()图9-1-23A．3B．4C．5D．6B[开始a＝4，b＝6，n＝0，s＝0.第1次循环：a＝2，b＝4，a＝6，s＝6，n＝1；第2次循环：a＝－2，b＝6，a＝4，s＝10，n＝2；第3次循环：a＝2，b＝4，a＝6，s＝16，n＝3；第4次循环：a＝－2，b＝6，a＝4，s＝20，n＝4.此时，满足条件s>16，退出循环，输出n＝4.故选B.] 2．(2017·长沙一中质检)图9-1-24如图9-1-24所示的算法框图，如果输入n＝3，则输出的S＝()A.67B．37C.89D．49B[第一次循环：S＝11×3，i＝2；第二次循环：S＝11×3＋13×5，i＝3；第三次循环：S＝11×3＋13×5＋15×7，i＝4，满足循环条件，结束循环．故输出S＝11×3＋13×5＋15×7＝12⎝⎛⎭⎪⎫1－13＋13－15＋15－17＝37，故选B.]3．执行如图9-1-25所示的算法框图，若输入的x的值为1，则输出的n的值为________.【导学号：66482434】图9-1-253[按照算法框图逐一执行．由x2－4x＋3≤0，解得1≤x≤3.当x＝1时，满足1≤x≤3，所以x＝1＋1＝2，n＝0＋1＝1；当x＝2时，满足1≤x≤3，所以x＝2＋1＝3，n＝1＋1＝2；当x＝3时，满足1≤x≤3，所以x＝3＋1＝4，n＝2＋1＝3；当x ＝4时，不满足1≤x ≤3，所以输出n ＝3.]4．关于函数f (x )＝⎩⎨⎧－x ，1＜x ≤4，cos x ，－1≤x ≤1的算法框图如图9-1-26所示，现输入区间[a ，b ]，则输出的区间是________．图9-1-26[0,1] [由算法框图的第一个判断条件为f (x )＞0，当f (x )＝cos x ，x ∈[－1,1]时满足．然后进入第二个判断框，需要解不等式f ′(x )＝－sin x ≤0，即0≤x ≤1.故输出区间为[0,1]．]。

单元训练（4）算法初步（一）1、当7,3m n ==时,执行如图所示的程序框图,输出的S 值为( )A.7B.42C.210D.8402、执行如图所示的程序框图,如果输出3s =,那么判断框内应填入的条件是( )A. 6k ≤?B. 7k ≤?C. 8k ≤?D. 9k ≤?3、如图所示,程序框图(算法流程图)的输出结果是( )A.34B.55C.78D.894、执行如图所示的程序框图,如果输入的[]2,2t ∈-,则输出的S 属于( )A. []6,2--B. []5,1--C. []4,5-D. [3,6]-5、根据下列算法语句,当输入为时,输出的值为( )A.25B.30C.31D.616、执行下面的程序框图,若输入的a ,b ,k 分别为1,2,3,则输出的M = ( )A. 20 3B. 7 2C. 16 5D. 15 87、算法的有穷性是指( )A.算法必须包含输出B.算法中每个操作步骤都是可执行的C.算法的步骤必须有限D.以上说法均不正确8、阅读如下程序框图,运行相应的程序, 则程序运行后输出的结果为( )A.7B.9C.10D.11答案1.C2.B解析：第一步, ()2log 1log 3ks s k =⋅+=,213k =+=;第二步, ()232log 1log 3log 4log 4ks s k =⋅+=⋅=,314k =+=;第三步, ()242log 1log 4log 5log 5ks s k =⋅+=⋅=,5k =;…第n 步, ()212log 1log (2)log (2)n s n n n +=+⋅+=+,2k n =+,若输出3s =,则()2log 23n +=,28n +=,6n =,28k n =+=,说明8k =时结束,故应填是7k ≤.选B .3.B解析：由题中程序框图知1x =,1y =,2z =;1x =,2y =,3z =;2x =,3y =,5z =;3x =,5y =,8z =;5x =,8y =,13z =;8x =,13y =,21z =;13x =,21y =,34z =;21x =,34y =,55z =,跳出循环.故输出结果是55.4.D解析：若02t ≤≤,则不满足条件输出[]33,1S t =-∈--,当20t -≤<时, 221(1,9]t +∈,此时不满足条件,输出(]2,6S ∈-,综上, []3,6S ∈-,故选D.5答案 C 解析 题目所给函数是分段函数,当时,,当时,.当输入时,.6.D 解析：第一次循环, 32M =,2a =,32b =,2n =;第二次循环, 83M =,32a =,83b =,3n =;第三次循环, 158M =,83a =,158b =,4n =,退出循环,输出M 为158.故选D.7.C解析：算法的程序即算法步骤是有限的,算法具有有限性.8.B解析：通过对程序框图的分析可知,该循环是一个根据判断条件不断累加的过程,∵7i =时, 135710lg lg lg lg lg 135799S =++++=>-,9i =时, 1357910lg lg lg lg lg lg 135791111S =+++++=<-,∴9i =,故选B.。