研究生课程有限元

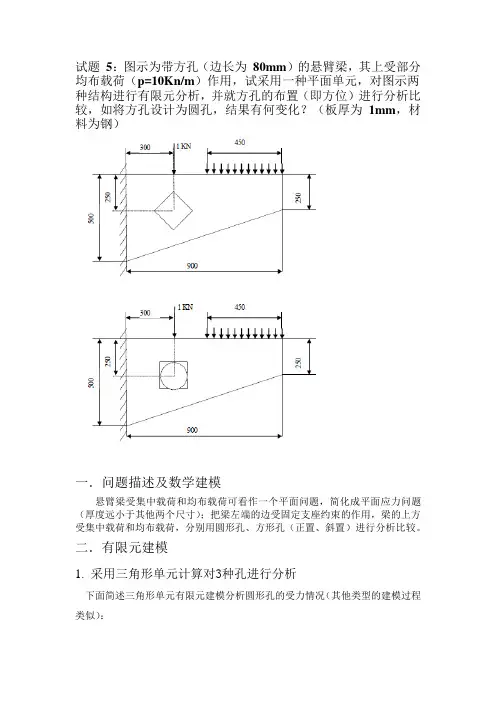
试题5：图示为带方孔（边长为80mm）的悬臂梁，其上受部分均布载荷（p=10Kn/m）作用，试采用一种平面单元，对图示两种结构进行有限元分析，并就方孔的布置（即方位）进行分析比较，如将方孔设计为圆孔，结果有何变化？（板厚为1mm，材料为钢）一．问题描述及数学建模悬臂梁受集中载荷和均布载荷可看作一个平面问题，简化成平面应力问题（厚度远小于其他两个尺寸）；把梁左端的边受固定支座约束的作用，梁的上方受集中载荷和均布载荷，分别用圆形孔、方形孔（正置、斜置）进行分析比较。

二．有限元建模1. 采用三角形单元计算对3种孔进行分析下面简述三角形单元有限元建模分析圆形孔的受力情况（其他类型的建模过程类似）：1.进入ANSYS【开始】→【程序】→ANSYS 12.0→File→change directory→Job Name:problem5→Run2．设置计算类型ANSYS Main Menu: Preferences→select Structural→OK3．选择单元类型单元是三节点常应变单元，可以用四节点退化表示。

ANSYS Main Menu: Preprocessor→Element Type→Add/Edit/Delete →Add →select Solid Quad 4 node 42→OK (back to Element Types window) →Options…→select K3: Plane Stress→OK→Close (the Element Type window)4. 定义材料参数材料为钢，可查找钢的参数并在有限元中定义，其中弹性模量E=210Gpa，泊松比v=0.3。

ANSYS Main Menu: Preprocessor →Material Props →Material Models →Structural →Linear →Elastic →Isotropic →input EX:2.1e11, PRXY:0.3→OK 5. 生成几何模型✓生成特征点ANSYS Main Menu: Preprocessor →Modeling →Create →Keypoints →In Active CS →依次输入六个点的坐标：input:1(0,0),2(900,250),3(900,500),4(0,500),5（300, 500),6(450,500)→OK✓生成坝体截面ANSYS Main Menu: Preprocessor →Modeling →Create →Areas →Arbitrary →Through KPS →依次连接1,2,3,6,5,4这六个特征点→OK6.网格划分ANSYS Main Menu: Preprocessor →Meshing→Size Cntrls→Manualsize→Lines →Picked Lines→选择梁外轮廓线→Size=40→Apply选择轮齿对称轴→Size=20→OkANSYS Main Menu: Preprocessor →Meshing →Mesh Tool→Mesh: Areas, Shape: Tri, Free→Mesh→Pick All (in Picking Menu) →Close( the Mesh Tool window)7.模型施加约束✓分别给左侧边施加全约束ANSYS Main Menu: Solution →Define Loads →Apply →Structural →Displacement →On lines→选择左侧边→OK →select:ALL DOF→OK✓给梁的上边施加集中载荷和分布载荷ANSYS Main Menu: Solution →Define Loads →Apply →Structural →Force →On Keypoints →拾取5节点Lab2: UY ，值为-1000→OKANSYS Main Menu: Solution →Define Loads →Apply →Structural →Pressure → On Lines→拾取5节点和6节点中间的线段FY，值为4500→OK8. 分析计算ANSYS Main Menu: Solution →Solve →Current LS →OK(to close the solve Current Load Step window) →OK9. 结果显示确定当前数据为最后时间步的数据ANSYS Main Menu: General Postproc →Read Result→Last Set查看在外力作用下的变形ANSYS Main Menu: General Postproc →Plot Results →Deformed Shape→select Def + Undeformed →OK查看节点位移分布情况Contour Plot →Nodal Solu… →select: DOF solution→Displacement vector sum→OK查看节点应力分布情况Contour Plot →Nodal Solu…→select: Stress→Stress intensity→Def + Undeformed→OK10. 退出系统ANSYS Utility Menu: File→Exit…→Save Everything→OK三．结果分析1.圆孔梁变形图，节点位移图，节点应力图2.斜置方孔变形图，节点位移图，节点应力图3.正置方孔变形图，节点位移图，节点应力图4. 将三种方案进行比较5.结论由实际情况可推知坝体X 向的变形和所受应力都为正，Y 向的变形和所受力均为负上面的结果与实际结果基本相符。

重庆大学研究生有限元大作业课程研究报告科目：有限元分析技术教师：阎春平姓名：色学号： 2专业：机械工程类别：学术上课时间： 2015 年 11 月至 2016 年 1 月考生成绩：阅卷评语：阅卷教师 (签名)有限元分析技术作业姓名: 色序号: 是学号: 2一、题目描述及要求钢结构的主梁为高160宽100厚14的方钢管，次梁为直径60厚10的圆钢管（单位为毫米），材料均为碳素结构钢Q235；该结构固定支撑点位于左右两端主梁和最中间。

主梁和次梁之间是固接。

试对在垂直于玻璃平面方向的2kPa 的面载荷（包括玻璃自重、钢结构自重、活载荷（人员与演出器械载荷）、风载荷等）作用下的舞台进行有限元分析。

二、题目分析根据序号为069，换算得钢结构框架为11列13行。

由于每个格子的大小为1×1（单位米），因此框架的外边框应为11000×13000（单位毫米）。

三、具体操作及分析求解1、准备工作执行Utility Menu：File → Clear＆start new 清除当前数据库并开始新的分析，更改文件名和文件标题，如图1.1。

选择GUI filter，执行Main Menu: Preferences → Structural → OK，如图1.2所示图1.1清除当前数据库并开始新的分析图1.2 设置GUI filter2、选择单元类型。

执行Main Menu: Preprocessor →Element Type →Add/Edit/Delete →Add→ select→ BEAM188，如图2.1。

之后点击OK(回到Element Types window)→Close图2.1 选择单元3、定义材料属性该钢结构材料为碳素结构钢Q235，其弹性模量为210GPa，执行Main Menu→Preprocessor →Material Props →Material Models →Structural →Linear→Elastic →Isotropic，此处协调单位制为mmkgs，故EX设为2.1E8, PRXY设置为0.3。

有限元复习宝典重点掌握一般问题的描述、模型简化、有限元的基本思想及分析原理、位移法求解基本过程、位移函数构造、单元特性、有限元计算的具体操作（单元刚阵形成、总纲阵组装）、边界条件处理（载荷等效/边界约束施加）、有限元分析的具体操作一．基本概念1. 平面应力/平面应变问题；空间问题/轴对称问题；板壳问题；杆梁问题；温度场；线性问题/非线性问题（材料非线性/几何非线性）等平面应力问题（1） 均匀薄板（2）载荷平行于板面且沿厚度方向均匀分布在六个应力分量中，只需要研究剩下的平行于XOY 平面的三个应力分量，即x y xy yx σσττ=、、 （000z zx xz zy yz σττττ=====，，）。

一般0z σ=，z ε并不一定等于零，但可由x σ及y σ求得，在分析问题时不必考虑。

于是只需要考虑x y xy εεγ、、三个应变分量即可。

平面应变问题（1） 纵向很长，且横截面沿纵向不变。

（2）载荷平行于横截面且沿纵向均匀分布z yz zx εγγ===只剩下三个应变分量x y xy εεγ、、。

也只需要考虑x y xy σστ、、三个应力分量即可 轴对称问题物体的几何形状、约束情况及所受外力都对称于空间的某一根轴轴对称单元的特点（与平面三角形单元的区别）：轴对称单元为圆环体，单元与单元间为节圆相连接；节点力与节点载荷是施加于节圆上的均布力；单元边界是一回转面；板壳问题一个方向的尺寸比另外两个方向尺寸小很多，且能承受弯矩的结构称为板壳结构，并把平分板壳结构上下表面的面称为中面。

如果中面是平面或平面组成的折平面，则称为平板；反之，中面为曲面的称为壳。

杆梁问题杆梁结构是指长度远大于其横断面尺寸的构件组成的系统。

在结构力学中常将承受轴力或扭矩的杆件成为杆，而将承受横向力和弯矩的杆件称为梁。

线性问题/非线性问题线性问题：基于小变形假设他，应力与应变，应力与位移，平衡方程都是线性的。

非线性问题：材料非线性(非线性弹性、非线性弹塑性)，几何非线性（大变形大应变如金属橡胶，小应变大位移如薄壁结构）空间问题、温度场问题，略2. 不同类型单元的节点自由度的理解和不同单元连接的处理不同单元连接的处理如果两相邻单元在连接处节点重合且节点自由度相同，可直接连接，则此时不同单元的刚度矩阵可类似单一单元分析一样直接组集。

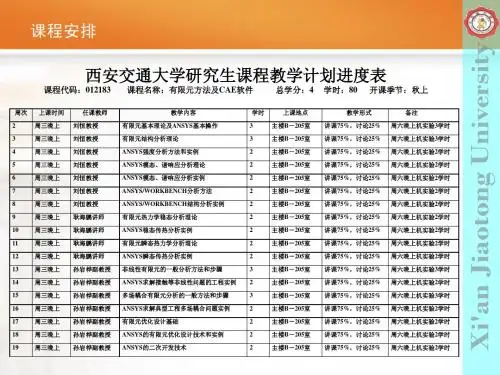
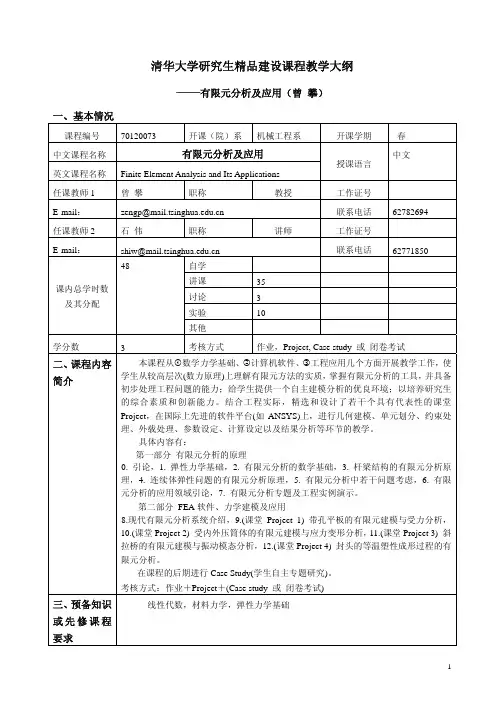
1.2.5 涉及多个自变函数的定积分驻值问题 i/ 泛函形式：⎰=ban n dt q q qq q q t L V ),,,,,,,,(2121 )(t q q i i = )(t q qi i = （l =1,2,…,n ） ii/ 求V 的驻值： iii/ ⎰∑∑==∂∂+∂∂=banr r r r nr rdt qqL q q L V ][11δδδ 利用分部积分法，可得：⎰∑∑==∂∂+∂∂∂∂-∂∂=babanr r r r nr r rq q Ldt q q Lt qLV }{})]([{11δδδ =0=> n 个Euler 方程(Euler 方程组)0)(=∂∂-∂∂r rqLdt d q L r =1,2,………,n (微分方程组)以及多种可能的边界条件。

* 上式在理论力学中称 Lagrange 方程，是具有 n 个参数自由度的保守系统运动方程。

* Hamilton 原理正是说明Lagrange 方程可来自于泛函驻值的求解。

* 若添加多个自变函数及他们的高阶导数，可获得与上一节类似结果。

1.2.6 重积分的驻值问题问题的提法：平面上有一区域Ω,Ω的边界为C ,要求在区域中找一个函数w (x ,y ),使下列重积分取驻值：J=⎰⎰Ωdxdy w w w y x F y x ),,,,(, yw w xw w y x ∂∂=∂∂=,)(2121φ==C C C C C在C 1 上，w w =（已知）目的：把上述泛函转化成偏微分方程的边值问题。

解：求 J 的一阶变分得：⎰⎰Ω∂∂+∂∂+∂∂=dxdy w w F w w F w wF J y yx x][δδδδ寻找 δw x , δw y 与δw 的关系，由Gauss 定理：⎰⎰⎰+=∂∂+∂∂Ωcds v u dxdy yv xu )cos cos ()(βαα,β是边界的外法线与x ,y 轴的夹角，C 是边界曲线的弧长。

第二章 弹性直梁问题的变分原理及有限元素法●讨论的问题：一变剖面的梁，一端()0=x 固支，另一端()l x =简支。

承受轴向拉力N ，分布横向载荷()x q 以及端点弯矩l M 的作用。

●控制微分方程及边界条件（以梁的挠度w 表示）q Nw dx w d EJ dxd q dx w d N dx w d EJ dxd=⎪⎪⎭⎫ ⎝⎛-⇐=-⎪⎪⎭⎫ ⎝⎛2222222222 支）基本边界条件（广义固处：在处：在⎪⎭⎪⎬⎫=====lw w l x dx dww w x 00,0ϕ0)(22=+=-l lM M M dxw d EJ自然边界条件● 称谓：把满足方程及全部边界条件的挠度叫真实挠度，精确解；把满足基本边界条件但不满足微分方程和自然边界条件的挠度叫（变形）可能挠度。

i)最小势能原理（变分原理） ● 把载荷看作是不变的已知函数，把挠度看作是可变的自变函数。

●整个系统的势能包括三部分：（1） 梁的应变能：⎪⎭⎫⎝⎛⇐⎪⎪⎭⎫ ⎝⎛=∏⎰⎰θMd dx dxwd EJ lb 212102222(2) 轴向应变能：⎰⎪⎭⎫ ⎝⎛=∏lNdx dx dw N 02221(3) 横向载荷势能：()l w M qwdx l lp'+-=∏⎰0(4) 系统总势能∏：w+d w222111⎪⎭⎫⎝⎛≈-+⎪⎭⎫ ⎝⎛=-dx dw dx dw dxdx ds后项取加号，是为着能够得到自然边界条件的结果()⎰'+⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧-⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=∏ll l w M dx qw dx dw N dx w d EJ 022222121 * 除w 为可变外，其余变量假定为已知的不变量。

● 最小势能原理：在所有变形可能的挠度中，精确解使系统的总势能取最小值。

●由于()w ∏是w 的二次函数，不用变分法而用较初等的方法也能作出数学证明。

证明过程：设()x w 是精确解，它满足微分方程及所有边界条件。

目 录061001 振动理论 (3)061002 有限元原理及工程应用 (3)062019 非线性连续介质力学 (3)062020 高等断裂力学 (4)062021 非线性动力学现代理论 (4)062022 动力学系统建模 (5)062023 现代振动测试技术 (5)062024 固体力学非线性数值方法 (5)062025 电磁机械力学 (6)062027 高等计算力学 (6)062028 工程结构动力分析 (7)062029 现代控制理论基础 (7)062031 振动力学实验技术 (8)062032 振动信号数据处理 (8)062037 固体中的超声波 (9)062041 模态分析及综合应用技术 (9)062042 智能结构与振动控制 (10)062043 有限元方法与ANSYS应用 (10)062044 现代力学测量技术 (11)062046 复合材料力学分析 (11)062048 工程疲劳与断裂 (12)062053 材料的力学行为 (12)062054 飞行器总体设计 (12)062055 高等飞行动力学 (13)062057 复合材料结构设计 (13)062059 飞行器结构动力分析原理与实践 (14)062060 可靠性设计基础 (14)062061 气动弹性原理 (14)062063 计算流固耦合力学 (15)062097 飞行器气动设计原理与实践 (15)062098 结构多场数值分析与设计 (16)062099 飞行器控制系统设计与实践 (16)062100 力学测量与无损检测 (17)062101 声学理论与工程应用 (17)062102 纳米材料力学 (18)062103 损伤力学 (19)062104 爆炸与冲击动力学 (19)062105 高等弹性理论 (19)062106 飞行器制导与控制原理 (20)062107 燃烧理论 (20)062108 实验空气动力学 (21)062109 先进制造技术基础 (21)062110 计算空气动力学 (21)062111 导弹飞行动力学与动态特性分析 (22)062112 飞行器健康管理 (22)062113 高等动力学 (22)062114 航天航空遥感原理与应用 (23)062115 现代组合导航技术 (23)062116 计算流体力学与实践 (23)062117 多学科优化设计 (24)062118 非线性振动理论及工程应用 (25)062119 高速转子动力学 (25)062120 工程随机系统动力分析 (25)062121 轻质结构及热防护理论 (26)061001 振动理论本课程是研究模型系统动态特性的基础课程，使学生在机械振动理论和振动测试领域获得较为系统和全面的知识，主要内容为单自由度、多自由度和杆梁的线性振动（固有振动、自由振动和强迫振动）的基本理论，多自由度系统的近似计算方法，传感器技术，振动过程的实验测量基本方法，结构的模态试验与振动信号数据处理等。

有限元技术应用与进展综述一、前言有限单元法又称有限元素法(Finite Element Method,FEM),是一种用于连续场分析的数值模拟技术。

它是20世纪50年代末60年代初兴起的应用数学、现代力学及计算机科学相互渗透、综合利用的边缘科学,是现代科学和工程计算方面令人鼓舞的重大成就之一。

有限元法最初应用在工程科学技术中,用于模拟并且解决工程力学、热学、电磁学等物理问题。

现在有限元法已成为工程和产品结构分析中必不可少的数值计算工具，广泛应用于机械制造、航空、造船、冶金、建筑、汽车、医疗等行业。

本文就以下几个方面介绍有限元法在实际中的应用和发展。

二、有限元技术发展现状有限元法是R.Courant于1943年首先提出的[1]。

自从提出有限元概念以来,有限元理论及其应用得到了迅速发展。

过去不能解决或能解决，但求解精度不高的问题 ,都得到了新的解决方案。

传统的FEM假设:分析域是无限的;材料是同质的,甚至在大部分的分析中认为材料是各向同性的;对边界条件简化处理。

但实际问题往往是分析域有限、材料各向异性或边界条件难以确定等[2]。

为解决这类问题,美国学者提出用GFEM(Generalized Finite Element Method)解决分析域内含有大量孔洞特征的问题[3];比利时学者提出HSM(the Hybrid metis Singular element of Membraneplate)解决实际开裂问题[4]。

在FEM应用领域不断扩展、求解精度不断提高的同时,FEM 也从分析比较向优化设计方向发展[5]。

印度Mahanty博士用ANSYS 对拖拉机前桥进行优化设计,结果不但降低了约40%的前桥自重,还避免了在制造过程中的大量焊接工艺,降低了生产成本。

FEM在国内的应用也十分广泛。

自从我国成功开发了国内第一个通用有限元程序系统JIGFEX后,有限元法渗透到工程分析的各个领域中,从大型的三峡工程到微米级器件都采用FEM进行分析[6-7],有限元技术在我国经济发展中拥有广阔的发展前景。

附件4：研究生课程教学大纲课程编号：小四宋体，右对齐，加粗工程有限元分析Finite Element Analysis In Engineering一、计划总学时：36 学分： 3 开课学期：Ⅱ授课方式：课堂教学考核方式：其他形式（大作业）二、适用专业：机械工程及其相关应用专业三、预修课程：高等数学、CAD三维设计基础、工程力学、材料力学四、教学目的：有限元分析方法是一种现代设计方法。

应用于工程设计中，可以提高产品质量、降低产品成本，是一种具有重要意义和巨大潜力的先进数字化分析技术。

该课程为机械工程及其相关专业硕士研究生的基础选修课。

本课程的目的是培养学生学会在机械设计中应用有限元分析技术来解决实际工程问题，掌握有限元分析方法的基本概念、基本原理、使用方法和解题步骤，并能够对轴对称结构、梁结构、桁架结构等变形进行具体的分析，熟悉ANSYS、ABAQUS、LS-DYNA等常用有限元分析软件在实际工程中的应用。

五、大纲内容及学时分配：第1章绪论（2学时）1.1 有限元分析的基本概念及其适用性1.2 有限元分析的发展概况及工程应用第2章常见有限元分析软件介绍（3学时）2.1 ANSYS介绍2.2 ABAQUS介绍2.3 LS-DYNA介绍2.4 HyperWorks介绍2.5 I-DEAS介绍第3章有限元分析方法的一般步骤（4学时）3.1 物体的离散化及插值函数3.2 平面问题有限元分析方法和程序3.3 边界条件和约束3.4 单元刚度矩阵和总刚度矩阵3.5 静力平衡问题求解第4章ANSYS7.0有限元分析的典型过程（4学时）4.1 前处理4.1.1 有限元模型的建立4.1.2 ANSYS 图元4.1.3 设置工作平面4.1.4 定义单元属性4.1.5 划分网格4.1.6 细划局部网格4.2 加载和求解4.2.1 加载4.2.2 求解4.3 结果后处理第5章静力分析（6学时）5.1 静力分析的基本步骤5.1.1 建立有限元模型5.1.2 施加载荷并求解5.1.3 查看分析结果5.2 梁结构静力分析5.2.1 自重对结构影响的分析5.2.2 均布载荷对结构影响的分析5.2.3 三维梁受集中载荷弯曲的分析5.3 桁架结构静力分析5.3.1 二维桁架分析5.3.2 三维桁架分析5.4 平面应力分析5.4.1 平面应力分析实例5.4.2 通过自定义路径查看分析结果5.4.3 P法分析第6章非线性分析（4学时）6.1 非线性分析简介6.1.1 非线性行为的原因6.1.2 非线性分析的特殊性6.1.3 非线性分析的主要步骤及注意事项6.1.4 非线性分析实例6.2 几何非线性分析6.2.1 几何非线性分析的注意事项6.2.2 几何非线性分析实例6.2.3 屈服分析及实例6.3 材料非线性分析6.3.1 材料塑性理论介绍6.3.2 塑性分析选项6.3.3 材料非线性分析实例6.4 状态非线性分析6.4.1 接触分析类型及其主要分析步骤6.4.2 接触分析实例第7章动力学分析（4学时）7.1 动力学分析简介7.1.1 动力学分析的类型7.1.2 动力学分析建模的注意事项7.2 模态分析7.2.1 模态分析的主要步骤7.2.2 模态分析实例7.3 谐响应分析7.3.1 谐响应的分析方法7.3.2 谐响应分析步骤7.3.3 谐响应分析实例7.4 瞬态分析7.4.1 瞬态动力学分析的分析方法7.4.2 瞬态动力学分析的主要步骤7.4.3 瞬态动力学分析实例第8章APDL及其应用（3学时）8.1 APDL简介8.2 APDL应用实例分析第9章MATLAB语言及应用（4学时）9.1 基础准备及入门9.2 符合计算9.3 数值数组及向量化运算9.4 数值计算9.5 数据和函数可视化9.6 M文件和函数句柄9.7 Simulink仿真第10章ANSYS7.0拓扑优化设计方法（2学时）10.1 拓扑优化设计方法简介10.2 拓扑优化的主要步骤和实例分析六、教材及主要参考书：(一) 理论课教材1、张亚欧，谷志飞，宋勇等. ANSYS7.0有限元分析实用教程. 清华大学出版社，2004.2、张志涌，杨祖樱.MATLAB教程，北京：北京航空航天大学出版社，2006.(二) 主要参考书1、李亚智．有限元法基础与程序设计．科学出版社，2004.2、李黎明．Ansys有限元分析实用教程．清华大学出版社，2005.3、曾攀. 有限元分析及应用. 清华大学出版社，2004.4、周昌玉，贺小华. 有限元分析的基本方法及工程应用研究. 化学工业出版社，2006.5、曹戈，赵阳. MTALAB实用教程，北京：清华大学出版社，2005.6、朱衡君，肖燕彩，邱成. MA TLAB语言及实践教程，北京：北京交通大学出版社，2005.七、任课老师：杨志贤，申祥八、大纲撰写人：杨志贤，申祥填表说明：1．开课学期请填写Ⅰ或Ⅱ2．授课方式：课堂教学、课堂教学与研讨、研讨、其他形式，其他形式请注明3．考核方式：笔试（开卷、闭卷），论文报告，其他形式，其他形式请注明。

研究生学位课《弹性力学及有限元》的创新教学研究论文（大全）第一篇：研究生学位课《弹性力学及有限元》的创新教学研究论文（大全）针对研究生学位课《弹性力学及有限元》理论性强，逻辑严谨、直观性差、抽象、难理解等基本特点，该文在教学内容、教学方法、教学手段三方面进行教学模式创新探索。

将现代教学手段与传统教学模式有机结合起来，将专业知识与工程实例溶入到理论教学之中，使枯燥抽象的理论知识变得生动实际，从而激发学生的学习兴趣和创新能力。

研究生学位课程《弹性力学及有限元》是一门理论性兼应用性极强的课程：一方面，理论性上，弹性力学的研究方法严密，基本概念及理论内容十分抽象，公式严谨难以理解，即使对一些简化的模型问题进行求解，通常需要大量的运用高数知识与理论，涉及微积分和常微分方程，更多运用偏微分方程相关思想与知识;另一方面，应用性上，弹性力学及有限元主要分析各种工程材料和工程结构在受力过后的变形状况，需要研究生对工程实例实践有自己的感性认识，能够将理论知识的分析与工程实际的例子联系起来。

因此，该课程对研究生的高等数学的基础思想和工程背景要求高，属于研究生教学期间难度系数比较大的一门学科。

该课程是机械工程专业必修的主干基础课程。

涉及弹性力学平面问题(平面应力与平面应变)基本理论、直角坐标及极坐标求解、差分法和变分法、有限单元法、空间问题的基本理论等方面的内容，综合性强[1]。

随着计算机技术的飞速发展，为弹性问题有限元法及弹塑性问题有限元法应用到机械工程的优化设计、制造分析提供了崭新途径和高效手段。

例如：采用先进的计算机数值模拟技术，人们可以在短短十几分钟之内完成手工作业需要花费数周时间才能完成的工作，大大缩短了设计和试制周期[2]。

如今几乎所有重要的机械产品和机械装备在研发阶段都必须采用数值方法进行计算分析，这已经成为探知复杂对象本质规律的定量分析手段。

数字化的“虚拟试验”在研发时做到了高效率与低成本的完美结合，其大规模巨容量的工程计算模拟在研发中起到核心支撑作用。

机械专业研究有限元的方向的硕士学位有限元分析是机械工程中非常重要的一项技术，它在设计和优化机械结构、预测和评估机械性能方面起着关键作用。

因此，对于机械专业的学生来说，研究有限元分析是一项具有重要意义的课题。

有限元分析是一种将复杂的连续体问题离散化为有限个简单子单元的数值计算方法。

通过将结构划分为许多小单元，我们可以更容易地处理和计算这些小单元的力学行为。

然后，通过将各个单元的边界条件和相互作用联系起来，我们可以得出整个结构的力学行为。

在有限元分析中，最关键的一步是建立合适的有限元模型。

这包括选择适当的单元类型、确定节点位置和边界条件，并选择合适的材料特性和加载方式。

通过合理地选择这些参数，我们可以准确地模拟和预测机械结构在不同工况下的响应和性能。

有限元分析在机械工程中具有广泛的应用。

例如，在汽车工业中，有限元分析可以用于评估车身结构的刚度和强度，优化车身设计，提高安全性能。

在航空航天工业中，有限元分析可以用于预测飞机结构的疲劳寿命和应力分布，指导结构优化和维修。

在机械制造行业中，有限元分析可以用于模拟和优化加工过程，提高零件的精度和质量。

随着计算机技术的不断发展，有限元分析的应用也越来越广泛。

现在，我们可以使用各种商业软件和开源软件来进行有限元分析，这大大提高了分析的效率和准确性。

此外，还有许多新的方法和技术被提出来，如拓扑优化、多物理场耦合等，使有限元分析更加强大和全面。

对于机械专业的硕士研究生来说，研究有限元分析是一项非常有前景和挑战性的课题。

通过深入研究有限元分析的原理和方法，他们可以更好地理解和应用这一技术，为机械工程的发展做出贡献。

此外，研究有限元分析还可以培养学生的分析和解决问题的能力，提高他们的工程实践能力。

机械专业研究有限元的方向的硕士学位是一项具有重要意义和广泛应用的课题。

通过研究有限元分析，我们可以更好地理解和预测机械结构的力学行为，优化设计和提高性能。

同时，这也是一个培养学生工程实践能力和解决问题能力的机会。