当前位置：文档之家 › 第14章达朗贝尔原理汇总

第14章达朗贝尔原理汇总

  • 格式：ppt
  • 大小：2.36 MB
  • 文档页数：50

下载文档原格式

  / 50

合集下载

第14章 达朗贝尔原理

第14章 达朗贝尔原理

置静止落下。求开始落下时杆AB的角加速度及A点支座反力。
解： 选杆AB为研究对象
虚加惯性力系：
FIt

ml
2
FIn
man
0
,
M IA

J A

ml 2
3
根据动静法，有
Ft 0 , FAt mg cos0 FIt 0
(1)
Fn 0 , FAn mg sin 0 FIn 0
c osqi

xi ri
s in q i

yi ri
M Ii mi xi zi 2 mi yi zi
令 J yz mi yi zi
J xz mi xi zi
分别称为对z 轴的惯性积，则惯性力系对x 轴的矩为
M Ix J xz J yz 2
Fi(e) Fi(i) FIi 0 ( i 1,2,.....,.n )
上式表明，质点系中每个质点上作用的外力、内力和惯性力在 形式上构成平衡力系。由静力学知，空间任意力系平衡的充分 必要条件是力系的主矢和对于任一点的主矩等于零，即
Fi(e) Fi(i) FIi 0 MO (Fi(e) ) MO (Fi(i) ) MO (FIi ) 0
综上所述,惯性力系向转轴上一点O简化的主矩为
MIO M Ixi M Iy j M Izk
如果刚体有质量对称平面,切该平面与转轴z垂直,简化中 心O取为 此平面与转轴的交点，则有
J yz mi yi zi 0, Jxz mi xi zi 0
则惯性力系简化的主矩为
M IO M Iz J z
1、刚体作平移 作平移时，刚体任一点i的加速度ai与质心的加速度aC相同，如 图，以O为简化中心，有
第十四章达朗贝尔原理资料

第十四章达朗贝尔原理资料

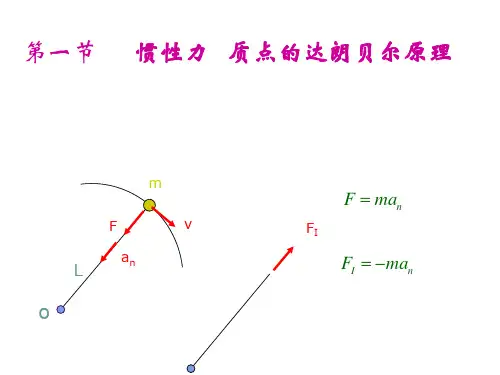
第十四章达朗贝尔原理动欝肉:用帝力学中研克平衡问题的方法来研克动力学问题・第一节惯性力a n质点的达朗贝余凍理F I = -man质点达朗贝余虑理作用于质点上的主动力F,釣束力F逢加惯性力F |扈形式上姐成平衡力糸.尸+仏+坊=0慣性力是人为地.級祖地加上去的，幷不真宾的作用蛊％体上。

达胡n余嫖理从形比上将动力学问题转化为符力学问题，它幷不故支动力学问题的卖质，质点矣际上也幷不平街。

F y+F Ny+F f y =0“动”代表研黑对象是动力学问题。

“鲁”代表研黑问题所用的方法是静力学方廉动静出的解題过程：1＞分析境点所受的主动力和釣束力；2, 分析填点的运动，确走加速度；3. 衣填点上加上与加速度方向相反的慣性力。

—♦F/ = -ma4、用鑫平衡方程求解尸+丘+斤=0第二节质点糸的达朗贝余斥理质点糸达朗贝余療理—► —►—►F M +F* — 0对于每•个填A Fj +质点糸中毎个质点上作用的主动力，釣隶力和它的慣性力在形此上组成平衡力糸.玖=工即+工理）+工尸〃=0M。

=工M,,（砂））+工M。

（叩）+ 工M。

（F,） = 0工申+工礼=0工收（炉）+工见伉）二0例题1 汽车连同货杨的总质量是力,其质心c With o多汽车以加速度日沿水平道路行驶肘，求地面给前・后轮的铅直反力。

轮子的质量不计。

达朗贝尔原理后轮的水平距离分别是b和＜7 ,离地面的离度是片力一加牡+尸皿@ +（） = 0fn(gb +cih)则体作平动刖体作走粕转动1 •需粘不通过贋心，但驸体作匀速转动 F[ = mr c a ) co第三节创体慣性力糸的简化 巧=》（・m 冋） =沖a c。

第14章达朗贝尔原理

第14章达朗贝尔原理

第14章 达朗伯原理14-1 均质圆盘质量为m ，半径为R ，OC = R/2。

求（1）圆盘的惯性力系向转轴O 简化的结果，并画图表示；（2）圆盘的惯性力系向质心C 简化的结果，并画图表示。

解：IR C F ma =- 而2tC R a α=，22n C R a ω= 12t t t t IR C IO ICF ma mR F F α====，212n n n nIR C IO IC F ma mR F F ω==== 方向与加速度方向相反向轴简化：22213()224IO O R M J mR m mR ααα⎡⎤==+=⎢⎥⎣⎦ 方向与α相反向质心C 简化：()()n t IC C IO C IO IO M M F M F M =+-22310242tIO R F mR mR αα=+⋅-=-14-2 调速器由两个质量为m 1的均质圆盘所组成，圆盘偏心的铰接于距转动轴为a 的A 、B 两点。

调速器以等角速度ω绕铅直轴转动，圆盘中心到悬挂点的距离为l ，如图所示。

调速器的外壳质量为m 2，并放在两个圆盘上。

如不及摩擦，求角速度ω与圆盘离铅垂线的偏角φ之间的关系。

解：由于对称，取B 为研究对象CωαCωα向质心C 简化 t C a nCa t IC F n ICF IC M C ωα向轴O 简化 t C a n Ca t IO F n IO F IOM 1m gI F BxF By F NF ϕ0BM=∑；1cos sin sin 0I N F l m gl F l ϕϕϕ--= （1）其中：212N F m g =，211(sin )nI CF m a m a l ϕω==+ 由（1）得：21121(sin )cos ()sin 02m a l l m m gl ϕωϕϕ+-+=即：2121(2)tan 2(sin )m m g m a l ϕωϕ+=+14-3 图示长方形均质平板，质量为27kg ，由两个销A 撤去销B 的瞬时平板的角加速度和销A 的约束反力。

理论力学14—达朗贝尔原理

理论力学14—达朗贝尔原理

a arccos(rw 2 )
g
14.2设质质点系点的系达由朗贝尔n 原个理质点组成, 其中任一质点i的质 量为mi, 其加速度为ai, 把作用在此质点上的力分为 主动力的合力Fi、约束力的合力为FNi，对这个质点 上假想地加上它的惯性力FIi＝-miai , 则由质点的达 朗贝尔原理, 有
Fi FNi FIi 0 (i 1, 2,, n)
14.设1 质一点质的达点朗质贝量尔原为理m, 加速度为a, 作用于质点的主 动力为F, 约束反力为FN 。由牛顿第二定律，有
ma F FN
将上式改写成
FI
m F
F FN ma 0
令
FI ma
FN
a
FI具有力的量纲, 且与质点的质量有关，称其为质点 的惯性力。它的大小等于质点的质量与加速度的乘
度w 绕该轴转动, 如图。求角速度w 与角 的关系。
解：以杆AB为研究对象, 受力如图。
杆AB匀速转动, 杆上距A点x 的微元段dxx sin )w 2
微 元 段 的 质 量 dm ＝ Pdx/gl 。 在 该 微 元 段
虚加惯性力dFI, 它的大小为
dFI
d m an
Pw 2
gl
sin
x
dx
于是整个杆的惯性力的合力的大小为
FI
l Pw2 sin x d x P lw2 sin
0 gl
2g
A
an
FAy FAx
A
dFI B
x
FI
PB x
设力FI 的作用点到点A的距离为d, 由合力矩定理, 有
l
FI (d cos ) 0 (x cos ) d FI
即
l Pw2 sin x 2 dx
14.达朗贝尔原理

14.达朗贝尔原理


FIR = − mac
16
17
二、定轴转动刚体 先讨论具有垂直于转轴的质量对称平面 的简单情况。 直线 i : 平动， 过Mi点， FIi = −mi ai 空间惯性力系—>平面惯性力系（质量对称面） O为转轴z与质量对称平面的交点，向O点简化： 主矢： 主矩： O
FIR = −maC
M IO = ∑ mO ( FIi ) + ∑ mO ( FIi )
例3 已知： 飞轮质量为m,半径为Ｒ,以匀角速度 已知： 飞轮质量为 半径为 以匀角速度 的影响. 的影响 求:轮缘横截面的张力. 轮缘横截面的张力.
ω 定轴转动，设 定轴转动，
轮辐质量不计,质量均布在较薄的轮缘上 不考虑重力 轮辐质量不计 质量均布在较薄的轮缘上,不考虑重力 质量均布在较薄的轮缘上
因
ϕ =ωt,得
Fy = (m + m )g + m eω cosωt 1 2 2
2
F = −m2eω2 sinωt x
M = m2gesin ωt +m2eω2hsin ωt
例6 已知：如图所示,电动绞车安装在梁上 梁的两端搁在支座上, 电动绞车安装在梁上,梁的两端搁在支座上 已知：如图所示 电动绞车安装在梁上 梁的两端搁在支座上 绞车与梁共重为P.绞盘半径为 绞盘半径为R,与电机转子固结在一 绞车与梁共重为 绞盘半径为 与电机转子固结在一 转动惯量为J 质心位于O 绞车以加速度a提升质 起,转动惯量为 ,质心位于 处.绞车以加速度 提升质 转动惯量为 质心位于 绞车以加速度 量为m的重物 其它尺寸如图. 的重物,其它尺寸如图 量为 的重物 其它尺寸如图 受到的附加约束力. 求：支座A，B受到的附加约束力 支座 ， 受到的附加约束力
第十四章 达朗贝尔原理

第十四章 达朗贝尔原理


FIiz 0 ,
M z (F i(e) ) M z (F Ii ) 0
实际应用时, 同静力学一样可任意选取研究对象, 列平衡 方程求解。
21
例题
达朗贝尔原理
r B
A
例题5
如图所示，滑轮的 半径为r，质量为m均匀分 布在轮缘上，可绕水平轴 转动。轮缘上跨过的软绳 的两端各挂质量为m1和m2 的重物,且m1 >m2 。绳的 重量不计，绳与滑轮之间 无相对滑动，轴承摩擦忽 略不计。求重物的加速度。
α
ω
15
例题
达朗贝尔原理
F* α F
ω
FN
mg
例题3
解： 以钢球为研究对象。设钢球的质
量为m。受力如图示。
鼓室以匀角速度ω转动，钢球尚
未脱离壳壁时，其加速度为：
an
D 2,
2
at 0
加惯性力，其大小为
F* m D2
2
应用质点动静法
Fn 0, FN mg cos F * 0
16
例题
26
例题
达朗贝尔原理
例题5
参见动画：达朗贝尔原理－例题5
27
例题
达朗贝尔原理
y FN
r
F1* mg
B A
a m2g
a m1g
F2*
例题5
解：以滑轮与两重物一起组成的质点系为研
究对象。 在系统中每个质点上假想地加上惯性力
后，可以应用达朗贝尔原理。
已知m1>m2，则重物的加速度a方向如图 所示。
)
M
O
(
FNi
)
M
O
(
FIi
)
0
Fi
F
十四章节达朗贝尔原理

十四章节达朗贝尔原理


d dt
( 12
Q g
r2
Q g
r2
1 2
Q g
r2
FP g
r
2
)
Qr
sin
FPr
2Q g
FP
r2
(Q sin
FP )r
a g(Q sin FP )
2Q F P
A a
Q
α
B
QC FP
例题4
第14章 达朗贝尔原理
飞球调速器的主轴O1y1以匀角速度转动。 试求调速器两臂的张角。设重锤C的质量为m1 ，飞球A，B的质量各为m2，各杆长均为l，杆重
W2
3 2
W1
A
MC (F) 0, JC FR 0
W2
F
JC
R
JCa R2
W2W1
2(W2
3 2
W1 )
例题
第14章 达朗贝尔原理
起重装置由匀质鼓轮D
（ 半 径 为 R ， 重 为 W1 ） 及 均 质 梁 AB （ 长 l=4R ， 重 W2=W1 ） 组成，鼓轮通过电机C（质量
FI mrc 2
2.转轴通过质心,但刚体作变速转动
a
M IO
O(C)
M IO Jc
3.刚体转轴通过质心并作匀速转动
O(C)
(c)
刚体的惯性力系自行平衡
刚体作平面运动
FI
C
aC M IC
FI mac
M Ic Jc
例题2
第14章 达朗贝尔原理
如图所示，滑轮的半径为r，质量为m均匀分 布在轮缘上，可绕水平轴转动。轮缘上跨过的软 绳的两端各挂质量为m1和m2的重物,且m1 >m2 。 绳的重量不计，绳与滑轮之间无相对滑动，轴承
第十四章 达朗贝尔原理

第十四章 达朗贝尔原理


O
O
O
J k
O
2 i
M
IO
F
i

Ii
n Ii
R
O
I
* 结论：
I
R M a
IO O
C
（过O点）
a m F r C a
n i
i C

M J
（与反向）

* 特殊情况分析
a
F
n I
C
M C
O
IO
C
e
a
n C
F

ea
F
O
n I
n C

I

M
IO
O
g mg mg
ml 9 1 3 9 g ml g 2 7l 2 7l 7l
2 mg 7
初始均质圆柱静止于 A处，受微小干扰后纯滚 而下，
求：轮心滚过任一距离 S时，轮心的加速度、 A处反力
X
A
Y
A
A
S


C
M
A
P

a
B
C
v
C
O
N
Ii
F
(e) i
i
即：
F
Ii
[ F F N F ] 0 (e) (i ) M O[ F i F i N i F Ii ] 0
(e) (i ) i i i
内力的主矢、主矩 0
F
a
(i ) i
i
m
i

Y
当圆盘以启动时：
A
M A
理论力学达朗贝尔原理

理论力学达朗贝尔原理


Foy

P
P g
R

P 3
（4）
Fxi 0 Fox FInR 0
将（2）式代入有
Fox


P g
R 2


4 3
P
（5）
理论力学电子教程
第十四章 达朗伯原理
例14-3 滚子半径为R，质量为m，质心在其对称中心C点，如 图(a)所示。在滚子得鼓轮上缠绕细绳，已知水平力沿着细绳 作用，使滚子在粗糙水平面上作无滑动得滚动。鼓轮得半径
§14-1 惯性力的基本概念
受非零力系作用的物体将改变运动状态。
由于物体具有惯性，力图保持其惯性运动，所以它 同时给予施力体以反作用力，这种反作用力称为惯性力 。例如，一质量为m的小球M，用细绳系住，绳的另一端 用手握住，使小球在水平面内作匀速圆周运动，其速度 为v，半径为r，如图14－1所示。
理论力学电子教程
相应地 于是
ai ri ain ri 2
FIi mi ri FIni mi ri 2方向如图（b）。
M IO M O (FIi) M O (FIi ) M O (FIni ) (miri )ri ( miri2 )
理论力学电子教程
一、刚体作平行移动 在同一瞬时，平动刚体上各质点具有相同的加速度 a。
任一质点M i的惯性力为
FIi miai 达朗伯原理
可见各质点的惯性力的大小与各自的质量成正比，方向都 与共同的加速度相反。即此时平动刚体的惯性力系是一个同向 平行力系，各力大小与各点质点质量成正比，如图所示。
得出上述的结论有两个限制条件：
理论力学电子教程
第十四章 达朗伯原理
（1）刚体具有垂直于转轴系的质量对称平面；
014第十四章达朗伯原理

014第十四章达朗伯原理

第14章 达朗伯原理（动静法）§14-1 达朗伯原理例 1. 质量10kg m =的物块A 沿与铅垂面夹角060θ=的悬臂梁下滑，如图所示。

不计梁的自重，并忽略物块的尺寸，试求当物块下滑至距固定端O 的距离0.6m l =，加速度22m/s a =时固定端O 的约束反力。

解：取物块和悬臂梁一起为研究对象，受有主动力W ，固定端O 处的反力Ox F 、Oy F 及O M 。

施加惯性力g F 如图所示，g F ma =，方向与a图14-3相反，加在物块上。

根据达朗伯原理，列形式上的平衡方程0 sin 00 cos 0()0 sin 0Ox g Oy g O iO X F F Y F W F m F M Wl θθθ⎧=-=⎪=-+=⎨⎪=-=⎩∑∑∑可解得sin 17.32N Ox g F F θ== cos 88N Oy g F W F θ=-= sin 50.92N m O M Wl θ==⋅从本例可见，应用质点达朗伯原理求解时，在受力图上惯性力的方向要与加速度方向相反，惯性力的大小为g F ma =，不带负号。

例1.如图所示，物块A 、B 的重量均为W ，系在绳子的两端，滑轮的半径为R ，不计绳重及滑轮重，斜面光滑，斜面的倾角为θ，试求物块A 下降的加速度及轴承O 处的约束反力。

图14-4解：先取物块B 为研究对象，所受的外力为绳索的拉力T 、重力W、光滑斜面的约束反力B N ，虚加的惯性力为gB F ，如图所示。

取图所示坐标系，根据质点达朗伯原理，可列出平衡方程为 0Y '=∑ cos 0BNW θ-=可得c o s B N W θ=再取物块A 、B 及滑轮和绳索所组成的系统为研究对象。

质点系的外力有两个物块的重力W ，轴承O 的约束反力O X 和O Y ，及光滑斜面的约束反力B N 。

虚加上惯性力gA F 和gB F ，如图所示。

惯性力的大小为gA gB WF F a g==。

WFW达朗贝尔原理

WFW达朗贝尔原理


§ 14-2 刚体达朗贝尔原理
3. 刚体作平面运动
若取质心C为基点， 若取质心 为基点，则刚体的平面运动可以 为基点 分解为随质心C的平动和绕质心 的平动和绕质心（ 分解为随质心 的平动和绕质心（通过质心且垂 直于运动平面的轴）的转动。 直于运动平面的轴）的转动。 刚体上各质点的加速度及相应的惯性力也 可以分解为随质心的平动和绕质心轴的转动 随质心的平动和绕质心轴的转动两 可以分解为随质心的平动和绕质心轴的转动两 部分。 部分。 于是，此刚体的牵连平动惯性力 牵连平动惯性力可合成为 于是 ， 此刚体的 牵连平动惯性力 可合成为 作用线通过质心、且在对称面内的一个力F 作用线通过质心、且在对称面内的一个力 I。 因质心C在相对运动的转轴上， 故刚体 因质心 在相对运动的转轴上， 在相对运动的转轴上 的相对转动的惯性力合成为一力偶。 相对转动的惯性力合成为一力偶。
MI＝0
刚体平移时，惯性力系简化为通过刚体质心的合力。 刚体平移时，惯性力系简化为通过刚体质心的合力。
§ 14-2 刚体达朗贝尔原理
2. 刚体做定轴转动
具有质量对称平面的刚体绕垂直于对称平面的固定轴转动。 具有质量对称平面的刚体绕垂直于对称平面的固定轴转动。 设刚体绕固定轴Oz转动， 设刚体绕固定轴 转动，在任意瞬 转动 时的角速度为ω，角加速度为 。 时的角速度为 ，角加速度为α。 ● 主矢 z
F + FNi + FIi = 0 i
这表明， 在质点系运动的任一瞬时， 这表明 ， 在质点系运动的任一瞬时 ， 作用于每一质 点上的主动力、 点上的主动力、约束力和该质点的惯性力在形式上构成一 平衡力系。 平衡力系。 这就是质点系的达朗贝尔原理。 这就是质点系的达朗贝尔原理。
§ 14-2 刚体达朗贝尔原理

第十四章达朗贝尔原理


FF* 0
质点的达朗贝尔惯性力与作用于质点的真实力组成平衡力系
非自由质点的达朗贝尔原理 作用在质点上的主动力和约束力与假想施加
在质点上的惯性力，形式上组成平衡力系。
F + FN ＋ F* ＝0
F F
m
ma F FF* 0
Fm a0 F* ma
F F ma 反作用力
一摆长随时间改变的单摆如图示，摆长的变化规律 为l0vt，v为常值。试用达朗贝尔原理列写摆的运动微 分方程，并求出绳的张力F。
1m2vmgcrosmgr
2
v22g1 rco s
an
FN
a
mg
脱离球面：
FN 0
F n mcgos0
2 m 1 c go m s cg o 0 s
F*
F*n
FN
mg
cos 2 3
48.2o
v22g1 rco s v 2 gr 3
14.2 达朗贝尔惯性力系的简化
F1*
Fi* miai
质点系的达朗贝尔原理
作用于每个质点上的真实力与惯性力构成质点 形式上的平衡方程。
F eiF i*0
对于质点系而言，所有作用与每个质点的外力、
内力与质点的惯性力构成空间平衡力系。简化得到系 统形式上的平衡方程：
F i F i*0
i
i
M O F iM O F i* 0

i
质量为m、长为L的匀质杆
AB在图示位置无初速释放， 求 释放瞬时AB杆加速度、
柔索A、B内的拉力。
受力分析、运动分析，
aA
aC
加惯性力 F ma
F 0 :F m sg i n 0 x agsin
y

14达朗贝尔原理


解：1、以杆为研究 对象，受力分析如图 对象， 、 F ⅠC 刚好离开地面时，地面约束力为零。 刚好离开地面时，地面约束力为零。
= m2 a
∑M
A
= 0 m aRsin 30 −m gRcos30 = 0 2 2
o o
a = 3g
2、以整体为研究对象，受力分析如图 、以整体为研究对象， 得
1 2 a FA = ma, MIA = m R I 1 1 2 R
aA = anA + atA= aCx + aCy + atAC + anAC
绳BO刚剪断瞬时，杆角速度ω = 0 ，角加速度α ≠0。 BO刚剪断瞬时 杆角速度ω 刚剪断瞬时， 角加速度α
anAC = AC ·ω2 = 0
atAC = lα／2
t aAC
t aA
O
把 aA 投影到点A轨迹的法线 AO上 投影到点A AO上
MIx = ∑ x (F ) = ∑ x Fi +∑ x Fn M Ii M Ii M Ii
( )
( )
= ∑ irαcosθi zi +∑ −mrω2 sinθi zi ) mi ( ii
由
xi yi cos θi = , sinθi = 有 MI x =α∑mi x i z i−ω2∑mi y i z ri ri
第十四章 达朗贝尔原理(动静法) 达朗贝尔原理(动静法)
§ 14-1 惯性力 质点的达朗贝尔原理 惯性力·质点的达朗贝尔原理
m = F +F a N
F + F −m = 0 a N
令 有
F = −m a I
惯性力
F + FN + F = 0 I

第14章 达朗贝尔原理

第十四章 达朗贝尔原理1．①2332ωmr F IR =；②C IR ma F =，方向水平向左，C IA mra M 21=，转向为顺时针。

2.解：设圆盘的质量为m ，半径为r ，则（a ）2I ωmr F =，0I =O M（b ）2n I ωmr F =，αmr F =tI ，αα2I 23mr J M O O == （c ）0I =F ，0I =O M （d ）0I =F ，αα2I 21mr J M O O ==3.解：如图（a ）：设平板的质量为m ，长和宽分别为a 、b 。

αα375.3I =⋅=AC m F ααα5625.0])(121[222I =⋅++==AC m b a m J M A A∑=0)(F A M ；01.0I =-mg M A ；2r a d /s 04.47=α∑=0xF；0s i nI =-Ax F F θ；其中：6.053sin ==θ N 26.956.004.47375.3=⨯⨯=Ax F∑=0yF；0c o s I =-+mg F F Ay θ；8.054s i n ==θN 6.1378.004.47375.38.927=⨯⨯-⨯=Ay F4.解：如图（a ）：设AB 、BC 两部分的质量各为m = 3.0kg 。

直角构件ABC其加速度为a = a A ， 质心在O 处。

ma F 2I =()0O M =∑F ；04sin )(43cos 4cos =+--lF F l F l F B A A B ϕϕϕ （1）∑=0AD F ；0cos 2=-+ϕmg F F B A （2）图14-1（a ）（a ）图14-3（a ）I联立式（1）和式（2），得： A B F mg F 3+=N 38.5)13(41=-=mg F A ； N 5.4538.53=⨯+=mg F B5.解：1、图（a ）： ① Wr J O =a αWr mr =a 221αmrW2a =α （1） ② 绳中拉力为W （2）③∑=0xF ，0=Ox F（3）∑=0y F ，W F Oy = （4）2、图（b ）： ① b 2I 21αmr M O= （5）bI αr gWa g W F ==（6）∑=0O M ，0I I =-+W r r F M O（5）、（6）代入，得 )2(2b W mg r Wg+=α （7）② 绳中拉力（图c ）：∑=0y F ，W F T =+I bW Wmg mga g W W T 2b +=-= （8） ③ 轴承反力： ∑=0x F ，0=Ox F （9） ∑=0y F ，0I =-+W F F OyW mg mgWF Oy 2+=（10）由此可见，定滑轮的角加速度a α、b α，绳中拉，轴承反力均不相同。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

FT1＝
m2 g
2cos
,
FT1＝FT1
cos m1 m2 g m1l 2
质点的惯性力与动静法
例 题2
y 振动筛
y
平衡位置 O
y＝a sin t
求：颗粒脱离台面的 最小振动频率
质点的惯性力与动静法 例 题 2
解：通过分析受力、分析运动并施加惯性力，确定 颗粒脱离台面的位置和条件。
y
y
FI FN m
m1g (FT1 FT2 )cos 0
对于重锤 C
FT1＝FT3 ,
FT1＝
m2 g
2cos
,
FT1＝FT1
质点的惯性力与动静法 例 题 1
解：
Fx1 0 Fy1 0
FT1＝FT3 ,
m1l 2sin (FT1 FT2 )sin 0
m1g (FT1 FT2 )cos 0
Wsin
W g
l
2
W 4
sin
CR W1
动静法应用于刚体的 动约束力分析
例 题5
半径为R、重量为W1的 大圆轮，由绳索牵引，在
O
重量为W2的重物A的作用 下，在水平地面上作纯滚
动，系统中的小圆轮重量
忽略不计。
A
求：大圆轮与地面之间
的滑动摩擦力
W2
动静法应用于刚体的 动约束力分析
例 题5
CR
W1
F FN
FO
解：1、受力分析
y
考察整个系统，有4个未知
O
FO 约束力。
x
如果直接采用动静法，需
将系统拆开。因为系统为一
个自由度，所以考虑先应用
A
动能定理，求出加速度，再 对大圆轮应用动静法。
W2
1 2
W2 g
v2
1 2
W1 g
v2
1 2
(1 2
W1 g
R2 )(
v )2 R
T0
W2
s
动静法应用于刚体的 动约束力分析
达朗贝尔原理与相关的动量定理和动量矩定理相一致。
质点的惯性力与动静法
动静法
应用达朗贝尔原理求解非自由质点动约束力的方法
F + FN ＋ FI ＝0 FI ＝－ m a
1、分析质点所受的主动力和约束力； 2、分析质点的运动，确定加速度； 3、在质点上施加与加速度方向相反的惯性力。
动静法应用于刚体的 动约束力分析
平衡位置
＝ g
a
质点的惯性力与动静法 例 题 2
解：通过分析受力、分析运动并施加惯性力，确定 颗粒脱离台面的位置和条件。
y
应用动静法
FN W ma 2sin t＝0
O y FN
ma
平衡位置 FN＝W＋ma 2sin t 0
颗粒在平衡位置以下时不会 脱离台面。
W FI
质点的惯性力与动静法 例 题2
达朗贝尔原理与动静法为解决非自由质点系 的动力学问题提供了有别于动力学普遍定理的另 外一类方法。
达朗贝尔原理一方面广泛应用于刚体动力学 求解动约束力；另一方面又普遍应用于弹性杆件 求解动应力。
结论与讨论 刚体惯性力系的简化结果
刚体惯性力系的主矢与刚体运动形式无关
1、平移
FIR ＝－m aC
2、定轴转动
ya W 平衡位置
O
O 平衡位置 y FN
ma
W FI
质点的惯性力与动静法 例 题 2
解：通过分析受力、分析运动并施加惯性力，确定 颗粒脱离台面的位置和条件。
应用动静法 y
FI＝ma 2sin t
FI FN m
ya W
O
FN－W＋ma 2sin t＝0
颗粒脱离台面的条件 FN＝0，
sin t＝1时， 最小。
动静法应用于刚体的 动约束力分析
例题4
解：1、运动分析
杆件OA绕O轴作定轴转动，假定
转动角速度和角加速度分别为和 。
2、受力分析 假设O处有沿着杆件轴线和垂直 于杆件轴线方向约束力； 杆件上由于定轴转动而产生的分 布惯性力向O处简化的结果为
FIτ ，FIn , M IO
动静法应用于刚体的 动约束力分析
结论与讨论
关于达朗贝尔原理和动静法 刚体惯性力系的简化结果 达朗贝尔惯性力与非惯性系中惯性力 惯性力系主矢和主矩与质点系动量和 动量矩 引起轴承动约束力的几种情形 几个实际问题
结论与讨论
关于达朗贝尔原理 和动静法
引进惯性力的概念，将动力学系统的二阶运 动量表示为惯性力，进而应用静力学方法研究动 力学问题 —— 达朗贝尔原理。
2
0， ＝3g
2l
sin
d 3g (1- cos )
dt
l
动静法应用于刚体的 动约束力分析
例题4
FIτ
W l
g2
FIn
W g
l 2
2
M IO JO
解： 3、应用动静法先求未知运动量
和 ，再计算动约束力：
d 3g (1- cos )
dt
lFx 0FOxW gl 22
Wcos
例 题5
CR
W1
F FN
FOy
O
FOx
A
如果直接采用动静法，需 将系统拆开。因为系统为一 个自由度，所以考虑先应用 动能定理，求出加速度，再 对大圆轮应用动静法。
W2
1 2
W2 g
v2
1 2
W1 g
v2
1 2
(1 2
W1 g
R2 )(
v )2 R
T0
W2
s
1 2
(W2 g
3 2
W1 )v2 g
T0
Fx1 0 Fy1 0
m1l 2sin (FT1 FT2 )sin 0 m1g (FT1 FT2 )cos 0
质点的惯性力与动静法 例 题 1
FT2
FT3
F´T1
解：
B FI
C
3、应用动静法：
FT1 m1 g
Fx1 0 Fy1 0
对于球 B m2 g
m1l 2sin (FT1 FT2 )sin 0
1. 质点
F + FN＝ FR =m a FI
F + FN +(－ m a) ＝0
F + FN ＋ FI ＝0
a
F m
vF
a
m
FR
FN
2.质点系
主动力系 F1 ,F2 , ,Fi , ,Fn
约束力系 FN1 ,FN2 , ,FNi , ,FNn
惯性力系 FI1 ,FI 2 ,L ,FIi ,L ,FIn
几个工程实际问题
爆
几 个 工 程 实 际 问 题
破 时 烟 囱 怎 样 倒 塌
几 个 工 程 实 际 问 题
惯性力
定义：由于物体具有惯性，抵抗其 FI
运动状态改变，而给予外界 的一种反作用力。
大小： FI = ma
FI ma 方向： FI与a的方向相反
作用点：在施力物体上
动静法(达朗伯原理)
主矩 M IC＝0
定轴转动(向轴心点简化) 主矢 大小： FIO = Mac
a
i
FIin
a FIi a mi
τ
CC n C
FIO＝－m aC
方向： FIO与ac的方向相反
a
n i
作用点：刚体轴心O上 MIO O
Fn IO FIO
主矩
F IO
M
＝
IO
M
O
(
Fτ Ii
)
＝－( miri2 )
＝－ J O
动静法应用于刚体的 动约束力分析
例题3
解：3、应用动静法
Fx 0
FBx ma FNAsin 0
FBx
W 2
sin2
2
a g
(1
cos
2
)
动静法应用于刚体的 动约束力分析
例题3
解：3、应用动静法
Fy 0
FBy W FNAcos 0
FBy
W (1-
g 4a 4g
sin 2 )
aτ C
3、平面运动 FIR ＝－maC
结论与讨论 刚体惯性力系的简化结果
惯性力系的主矩 —— 惯性力系的主矩与刚体的 运动形式有关。
1、平移
M IC ＝0
2、定轴转动
M IO＝－J O
3、平面运动
M IC＝－JC
结论与讨论
达朗贝尔惯性力与 非惯性系中惯性力
达朗贝尔惯性力
FI ＝－ma a－绝对加速度
0
FOx
W g
l 2
2
Wcos
W 2
(3 - 5cos )
动静法应用于刚体的 动约束力分析
例题4
FIτ
W l
g2
FIn
W g
l 2
2
M IO JO
解： 3、应用动静法先求未知运动量
和 ，再计算动约束力：
d 3g (1- cos )
dt
l
Fy 0
FOy
W g
l
2
Wsin
0
FOy
FT2 B
FT3
F´T1
C
FT1 m1 g
m2 g
质点的惯性力与动静法 例 题 1
解： 2、分析运动：施加惯性力。
FT2
FT3
F´T1
球绕O1y1轴作等速圆周 运动，惯性力方向与法向
B FI C
加速度方向相反，其值为
FI＝m1l 2sin
FT1 m1 g
重锤静止，无惯性力。 m2 g
3、应用动静法：