当前位置：文档之家 › 达朗贝尔原理解剖

达朗贝尔原理解剖

  • 格式：ppt
  • 大小：7.92 MB
  • 文档页数：67

下载文档原格式

  / 67

合集下载

第十四章达朗贝尔原理资料

第十四章达朗贝尔原理资料

第十四章达朗贝尔原理动欝肉:用帝力学中研克平衡问题的方法来研克动力学问题・第一节惯性力a n质点的达朗贝余凍理F I = -man质点达朗贝余虑理作用于质点上的主动力F,釣束力F逢加惯性力F |扈形式上姐成平衡力糸.尸+仏+坊=0慣性力是人为地.級祖地加上去的，幷不真宾的作用蛊％体上。

达胡n余嫖理从形比上将动力学问题转化为符力学问题，它幷不故支动力学问题的卖质，质点矣际上也幷不平街。

F y+F Ny+F f y =0“动”代表研黑对象是动力学问题。

“鲁”代表研黑问题所用的方法是静力学方廉动静出的解題过程：1＞分析境点所受的主动力和釣束力；2, 分析填点的运动，确走加速度；3. 衣填点上加上与加速度方向相反的慣性力。

—♦F/ = -ma4、用鑫平衡方程求解尸+丘+斤=0第二节质点糸的达朗贝余斥理质点糸达朗贝余療理—► —►—►F M +F* — 0对于每•个填A Fj +质点糸中毎个质点上作用的主动力，釣隶力和它的慣性力在形此上组成平衡力糸.玖=工即+工理）+工尸〃=0M。

=工M,,（砂））+工M。

（叩）+ 工M。

（F,） = 0工申+工礼=0工收（炉）+工见伉）二0例题1 汽车连同货杨的总质量是力,其质心c With o多汽车以加速度日沿水平道路行驶肘，求地面给前・后轮的铅直反力。

轮子的质量不计。

达朗贝尔原理后轮的水平距离分别是b和＜7 ,离地面的离度是片力一加牡+尸皿@ +（） = 0fn(gb +cih)则体作平动刖体作走粕转动1 •需粘不通过贋心，但驸体作匀速转动 F[ = mr c a ) co第三节创体慣性力糸的简化 巧=》（・m 冋） =沖a c。

《达朗贝尔原理》课件

《达朗贝尔原理》课件
达朗贝尔原理的微分方程形式为：dM/dt=∫F·d(dr/dt)dr，其中dM/dt表示动量 矩对时间的变化率，dr/dt表示速度矢量，∫F·d(dr/dt)dr表示力矩对时间的积分 。
该微分方程描述了刚体在力矩作用下的动态行为，是刚体动力学中的基本方程之 一。
达朗贝尔原理的积分方程形式
达朗贝尔原理的积分方程形式为：M(t2)-M(t1)=∫t1t2F·dr， 其中M(t2)和M(t1)分别表示刚体在时刻t2和t1的动量矩， ∫t1t2F·dr表示在时间t1到t2之间力矩的积分。
船舶工程
用于分析船舶的运动特性和稳定性。
02
达朗贝尔原理的数学表达
达朗贝尔原理的公式表达
达朗贝尔原理的公式表达为： M=∫F·dr，其中M表示刚体绕固定 点O转动的动量矩，F表示刚体上任 一点的速度矢量，dr表示矢径。
该公式描述了刚体在力矩作用下的运 动规律，是刚体动力学中的基本原理 之一。
达朗贝尔原理的微分方程形式
限制条件
达朗贝尔原理在处理复杂系统时，可能无法考虑所有 相互作用力和能量转换，导致预测精度下降。
与其他物理定律的互补性
与牛顿第三定律互补
达朗贝尔原理与牛顿第三定律互补，强调了 力和运动的相互关系。
与能量守恒定律的互补性
达朗贝尔原理在处理保守系统时，与能量守 恒定律相一致，但在非保守系统中存在差异
。
详细描述
在弹性力学中，达朗贝尔原理可以用来分析 各种复杂的力学问题，如梁的弯曲、板的变 形等。通过应用该原理，我们可以建立各种 弹性力学问题的数学模型，并进一步求解其 解析解或近似解。
05
达朗贝尔原理的局限性
适用范围和限制条件
适用范围
达朗贝尔原理主要适用于线性、保守的力学系统。对 于非线性、非保守系统，达朗贝尔原理可能不适用。

达朗贝尔原理

达朗贝尔原理

α O
有质量对M称O面 F且i转e 轴垂直M此O面F的Ii 定轴0转动
的刚体, 其上达朗伯惯性力系向对称面与
C
定轴的交点O简化可得一力和一力偶.
FI
M IO
惯性力: FI M aC
惯性力偶: M IO JO
3. 刚体平面运动( 刚体有质量对称面且运动平面平行于此面).
刚体平面运动是随质心的平动和绕质心 的转动的合成. 其上的达
下面, 我们将对常见的几种运动的刚体上的达氏惯性力进行简化.
§14 – 3 刚体惯性力系的简化
1. 刚体的平动
FI C
刚体作平动, 其上所有点的加速度矢都相等. 因而惯性力系是一同向平行力系. 这个力系 与重力系类似, 其合力过质心C .
a a
C
i
F I
F Ii
mi ai
mi a C M a C
§13 – 1 惯性力 . 质点的达朗贝尔原理
1. 达朗贝尔惯性力:
FI
定义: F I ma
m
F
FN ma
▲: 达朗贝尔惯性力是在惯性参考系下定 义的惯性力, 惯性力中所含的加速度是绝 对加速度 , 在合成运动的分析中, 它是相 对, 牵连和科氏加速度的总和.
2. 质点的达朗贝尔原理:
由动力学基本方程
这个‘ 平衡力系’ 显然是一个空间的平衡力系. 根据空间力系的 平衡理论 , 就是: 系统中的所有质点的达朗贝尔惯性力和外力系的 矢量和为零( 主矢为零), 以及这些力对任意点的矩的矢量和为零( 主 矩为零). 用数学式表示, 即是:
e
F i F Ii 0
M
O
F
e
i
M O
F Ii
0

达朗贝尔原理达朗贝尔原理是法国科学家达朗贝尔于1743年

达朗贝尔原理达朗贝尔原理是法国科学家达朗贝尔于1743年

第7章 达朗贝尔原理达朗贝尔原理是法国科学家达朗贝尔于1743年提出的，是分析力学的两个基本原理之一。

该原理揭示，对动力系统加入惯性力后，惯性力与外力构成平衡，因而提供一种用静力平衡方法处理动力学问题的普遍方法——动静法。

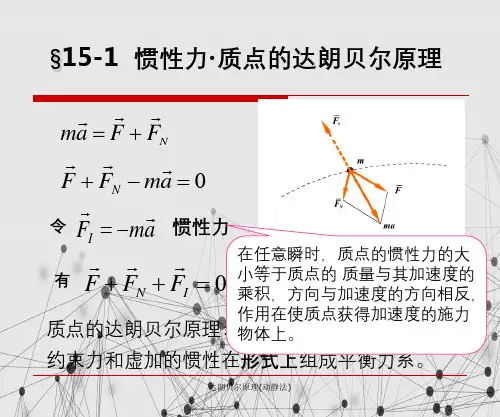
§7.1 质点系的达朗贝尔原理7.1.1 惯性力与质点的达朗贝尔原理1、质点达朗贝尔原理如图7.1所示，质量为m 的质点沿曲线轨道运动，受主动力F 和约束力N F 作用，由牛顿第二定律有N m +=F F a即0N m +-=F Fa 引入惯性力I m =-F a (7-1)则有0N I ++=F F F (7-2)这就是质点的达朗贝尔原理：作用在质点上的所有主动力、约束力和惯性力组成平衡力系。

这样，我们完全可以采用静力学的方法和技巧，求解动力学问题。

顺便指出，达朗贝尔原理作为分析力学的基本原理之一是不需要推导证明的。

这里由牛顿第二定律导出，可以说明它与牛顿力学在数学上的等价性。

问题7-1 如图所示，重为G 的小球用细绳悬挂，试求AC 绳断瞬时AB 绳的张力。

答 研究小球，加惯性力I F ，受力如图所示，由质点达朗贝尔原理，有0I T ++=F G F由力三角形有cos T F G =θ可见，加上惯性力，采用静力学中三力平衡的几何法求解决，直观简便。

2、惯性力的概念质点的惯性力I F 可以想象为：当质点加速运动时外部物质世界作用在质点上的一个场图7.1 质点达朗贝尔原理IF 问题7-1图力，其大小等于质点的质量与其加速度的乘积，方向与质点加速度方向相反。

惯性力与万有引力是完全等效的。

惯性力与参考系相关，如图7.2(a)所示，小球在旋转水平圆台上沿光滑直槽运动。

在地面惯性参考系观察，小球运动的绝对轨迹为螺旋线，见图7.2(b)，在水平面内受滑槽侧壁对它的作用力N F 作用，加速度如图所示；从转动圆台非惯性参考系观察，小球的运动轨迹沿槽直线，在半径方向，受牵连法向惯性力2()nnIe Ie F mr ω=F 作用，小球沿直槽加速向外运动。

达朗贝尔原理(动静法)

达朗贝尔原理(动静法)

达朗贝尔原理(动静法)
例15-1 用达朗贝尔原理求解
已知: m 0.1kg, l 0.3m,
60
求:
v, FT .
O θ l
达朗贝尔原理(动静法)
解: 先分析小球的受力和加速度，如图
FIn
v2
m an mlsin
mg FT FI 0
Fb 0, FT cos mg 0
Fn 0, FT sin FIn 0
解得
FT
mg
cos
1.96N
v
达朗贝尔原理(动静法)
FT l sin 2
m
2.1m s
§15-2 质点系的达朗贝尔原理
Fi FNi FIi 0
i 1,2,, n
记 Fi(e) 为作用于第i个质点上外力的合力.
F (i) i
为作用于第i个质点上内力的合力.
则有
Fie
FIR
Fie
miai maC
１ 刚体平移
惯性力系向质心简化.
由
M IC
d dt
LC
0
只简化为一个力 FIR maC
2 刚体定轴转动
大小为:
Ft Ii
mi ait
mi ri
Fn Ii
mi ain
mi ri 2
MIx
M x FIi
Mx
Fi Ii
Mx
Fn Ii
性力在形式上组成平衡力系。
达朗贝尔原理(动静法)
例15-2 如图所示,定滑轮 的半径为r,质量为m均匀分
布在轮缘上,绕水平轴Ｏ转
动.垮过滑轮的无重绳的两 端挂有质量为m1和m2的重 物(m１>m2),绳与轮间不打 滑,轴承摩擦忽略不计,求 重物的加速度.

理论力学经典课件第七章达朗贝尔原理

理论力学经典课件第七章达朗贝尔原理

•
又
d
dt
di ωi ωj dt
F1
aC C
F2
rC
Fi
A
M IA y
dj ωj ωi d k 0 x
m aC
dt
dt
故 M IA ( J x α z J y ω z 2 ) i ( J y α z J x ω z 2 ) j J z α k
7-4-3 轴承动约束力
• 设动约束力如图。
z
r
m
r
m
r
m
r
2r
2m
r
m
(a)
(b)
静,动
静
(c)
静,动
mr m
rm
(d)
静
7-4-4 动约束力效应及消除方法
1. C 0 Wc=0。
由 TTv W
R
1mvc211m2R22
C
2
23
m g ( 2 R 2 R c o s) + m g R ( 1 c o s) l
而 VC 2R ，
• 1)静约束力——与主动力平 衡
2)动约束力——与惯性力平衡
2.求解: 1)动量定理与动量矩定理
2)动静法 形式不同，本质相同。
7-4-2 惯性力系的简化
• 如图 已知ω 、α AB， l 向A点简化，且A-xyz
z
与刚体固结。
B
主矢 主矩
FIRmaC
MIA
d LA dt
而 L AJxω ziJyω zjJzω k
由 Mx 0
B
F BlyJx z Jyz 20 F B x
F By
F1
FByJxzlJyz2

达朗贝尔原理2刚体作定轴转动3刚体作平面运动惯性力的简化1


∴a cos－fsin g
整体
ΣMO = 0
M O－mgs sin = 0 ∴ M O = mgs sin
s
O

A
Fs = f FN
B
FI a
y
a FOy
O FOx FI
Fs
A

FN mg
MO
A
mg B x
Σ Fx = 0
Σ Fy = 0
mg cos－FI + FOx = 0 ∴ FOx =－mg cos
=0
∴a
=
4 M－W1R
g
3W1
R
A MI
B E
M + (W1+ W2 )
l 2
+ (W +
FI
)(
l －R)－M 2
I－lFAy
=
0
∴ FAy
=
13 12 W1+
M 6R
M
MI D
FCy
C
FCx
α
M W1
E
∑Fy = 0 FAy + FB－FI－W1－W2－W = 0
FAy C
FB
W1
a FI
W
∴ FB
FOy + mg sin = 0
∴FOy = mg sin
=
13 12 W1+
M 6R
∑Fx = 0 FA x = 0
FAx W2
E FI
W
例3. 质量m的物块A沿与铅垂面夹角为φ摩擦系数为f的悬臂梁下滑,
不计梁重，求物块下滑至离固定端O的距离为s时O端的约束力。
解： 物块A
FI = ma

达朗贝尔原理—搜狗百科

达朗贝尔原理—搜狗百科达朗贝尔原理d'Alembert principle研究有约束的质点系动力学问题的一个原理。

由J.le R.达朗贝尔于1743年提出而得名。

对于质点系内任一个质点，此原理的表达式为F ＋N－ma＝0，式中F为作用于质量为m的某一质点上的主动力，N 为质点系作用于质点的约束力，a为该质点的加速度。

从形式上看，上式与从牛顿运动方程F＋N＝ma中把ma移项所得结果相同。

于是，后人把－ma 看作惯性力而把达朗贝尔原理表述为：在质点受力运动的任何时刻，作用于质点的主动力、约束力和惯性力互相平衡。

利用达朗贝尔原理，可将质点系动力学问题化为静力学问题来解决，这种动静法的观点对力学的发展产生了积极的影响。

d'Alembert principle作用于一个物体的外力与动力的反作用之和等于零。

即F＋（-Ma）＋N=0 （1）其中M，a为物体质量和加速度，F为物体受到的直接外力，N为物体受到的约束反作用力（也是外力）。

在没有约束时，相应的N=0，（1）式成为F-Ma=0 （2）与牛顿的运动第二定律一致，只是进行了移项。

但这是概念上的变化，有下列重要意义：①用（2）式表达的是平衡关系，可以把动力学问题转化为静力学问题来处理。

②在有约束情况下，用（1）式非常有利；它与虚功原理结合后，可列出动力学的普遍方程。

③用于刚体的平面运动时，可利用平面静力学方法，使问题简化。

实际上，达朗贝尔原理还为不久后创立的分析力学打下了基础。

研究有约束的质点系动力学问题的一个原理。

由J.le R.达朗贝尔于1743年提出而得名。

对于质点系内任一个质点，此原理的表达式为F＋N－ma＝0，式中F为作用于质量为m的某一质点上的主动力，N 为质点系作用于质点的约束力，a为该质点的加速度。

从形式上看，上式与从牛顿运动方程F＋N＝ma中把ma移项所得结果相同。

于是，后人把－ma 看作惯性力而把达朗贝尔原理表述为：在质点受力运动的任何时刻，作用于质点的主动力、约束力和惯性力互相平衡。

第16章 达朗贝尔原理(动静法)


§16-1 惯性力 达朗贝尔原理
一、质点的惯性力、达朗贝尔原理
我们知道：
静力学问题： F 0 动力学问题： F 0
m
（主动力＋反力＝0）——静力学方程
而是 ma F F ma 0 F FI 0
F
——动力学方程
FI ma
aCx aCy a A aCA
在水平方向上投影： aCx a A cos 45 aCA sin 30
在铅直方向上投影： aCy a A sin 45 aCA cos 30
(4)
(5)
l aCA 2
至此，共5个方程，6个未知量
11
注：由此题可知，达朗贝尔原理与动量定理和动量矩定理等效。故要
求用达朗贝尔原理求解问题时，不能用此二定理，但可用动能定理。 例2（例14-11，刚体平面运动微分方程。 现用动静法求解） 均质杆AB，质量m，长l。在图示位 置释放。求此时杆的角加速度。 还记得前面如何求解的吗？ 回顾一下。 解：画杆受力、运动图，如图。

F N
P
FIP
所有惯性力和惯性力偶均已知，对整体列“平衡” 方程，可求出地面反力。 7
解：I. 求加速度aC 。 研究重物、轮子、滚子整体，画受力图如 图。其中惯性力和惯性力偶大小：
FIP FIC P P a aC g g Q aC g M IO M IC 1Q 2 r 2g
惯性力系： FIi mi aC
向质心简化：
a C r aC
C
FI
主矢： FI ΣFIi Σ(mi aC ) MaC 即 FI MaC ——惯性力 主矩： M IC ΣmC (FIi ) Σri '(mi aC ) Σmi ri 'aC MrC 'aC 0

动力学达朗贝尔原理-PPT课件


化为通过O点的一力和一力偶。 m
刚体惯性力系的简化
第6章 达朗贝尔原理
三、刚体作平面运动
一般取质心C为简化中心
F m a IR C
M M ( m a ) IC C i i
n M ( m a M ( m a C i i) C i i) JC
惯性力系简化为平面内一个力和一个力偶：惯性力通过质心， 大小等于质量与质心加速度的乘积， 方向与质心加速度方向相 反；惯性力偶矩大小等于通过质心且垂直于平面的轴的转动惯 量与角加速度的乘积，转向与角加速度的转向相反。


F 0
x
2 0
m 2 F R d R cos A 0 2 R 用相同方法 2 m R 计算FB FA 2
由于截面对称，任一横截面张力相同。
质点系的达朗贝尔原理
第6章 达朗贝尔原理
例二
滑轮半径为r，质量m均匀分布在轮缘上，绕水平轴转动。 轮缘上跨过的软绳的两端各挂质量为m1和m2的重物，且 m1 ＞m2 。绳的重量不计，绳与滑轮之间无相对滑动，摩擦不 计。求重物的加速度。 Fn

l
T
b
F 0
b
Tcos mg
n mg

T 1 . 9 6 N , v 2 . 1 m / s
F
n I
质点系的达朗贝尔原理
第6章 达朗贝尔原理
F F 0 i Ni Ii
F F F 0 Ii
F F 0
( e ) i Ii
( e ) i
( i ) i
M ( F ) M ( F ) 0
（d）
两种情形的定滑轮质量均为m，半径均为r。图a中的绳所受 拉力为W；图b中块重力为W。试分析两种情形下定滑轮的角 加速度、绳中拉力和定滑轮轴承处的约束反力是否相同。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
M0 Fie M0 FIi 0
应用动静法求解时，其解题步骤与静力学一样。 即：选取研究对象、画受力图、列平衡方程、求 解。
例 如图所示，定滑轮的半径为r，质量为m均匀 分布在轮缘上，绕水平轴Ｏ转动。垮过滑轮的
无重绳的两端挂有质量为m1和m2的重物（m１ >m2)，绳与轮间不打滑，轴承摩擦忽略不计， 求重物的加速度。
（平行于质量对称面）
假设刚体具有质量对称平面， 并且平行于该平面作平面运动 。此时，刚体的惯性力系可先 简化为质量对称平面内的平面 力系。
刚体平面运动可分解为：
绕质心轴的转动:
随质心C的平移：
M Ic JC
FIR maC （作用于质心C）
例 如图所示均质杆的质量为m，长为l，绕定轴 O转动的角速度为 ，角加速度为 。 求：惯性力系向点Ｏ简化的结果 （方向在图上画出）。
α 角随着加速度a的变化而变化，当a不变时， α 角 也不变。只要测出α 角，就能知道列车的加速度a 。
摆式加速计的原
动静法优点：
可以利用静力学研究平衡问题的方法研究动 力学问题；
给动力学问题提供了一种统一的解题格式。
§ 13-2 质点系的达朗贝尔原理
Fi FNi FIi 0
i 1,2,, n
解： FI1 m1a, FI 2 m2a
FIti mir mia , m1g m1a m2 g m2ar miar 0
由 miar mi ar mar
解得 a m1 m2 g m1 m2 m
例 飞轮质量为m，半径为Ｒ，以匀角速度 定 轴转动，设轮辐质量不计，质量均布在较薄 的轮缘上，不考虑重力的影响。
第十三章 达朗贝尔原理(动静法)
达朗贝尔是一位哲学家、数学家、 天文学家、力学家。
1743年，他发表了《论动力学》 一书，提出了达朗贝尔原理。
他假定：就整个物体而言，内部 反作用互相抵消了，对运动没有 任何贡献，而事实上另一组力把 运动传递给系统，使得有效力静 态地等于外力，这里说的“有效 力”即是惯性力。
FIR Fi e maC
１ 刚体平动 惯性力系向质心简化。
刚体平移时惯性力系合成为一过质心的合力。
2 刚体定轴转动 这里仅讨论具有垂直于转轴的质量 对称平面的简单情况。
直线i : 平移，过Mi点，F = −miai
空间惯性力系→平面惯性力系（质 量对称面内）
点O为转轴z与质量对称平面的交 点，向O点简化。
解：
FItO
m
l
2
FIOn
m
l 2
2
M IO
1 3
m l 2
例 如图所示，电动机定子及其外壳总质量为m1， 质心位于O处。转子的质量为m2，质心位于Ｃ 处，偏心矩ＯＣ＝e,图示平面为转子的质量对 称面。电动机用地角螺钉固定于水平基础上，
转O与水平基础间的距离为h。运动开始时，转
子质心Ｃ位于最低位置，转子以匀角速度
（1717-1783)
Let’s Go!!!
§ 13-1 惯性力·质点的达朗贝尔原理
ma F FN
F FN ma 0
令 FI ma 惯性力
有 F FN FI 0
质点的达朗贝尔原理：作用在质点的主动力、 约束力和虚加的惯性力在形式上组成平衡力系。
注意:
1. 惯性力是虚加的，并非真正作用在 质点上。
因
Fii 0,
M 0 Fi i 0,
有
Fi e FIi 0
M 0 Fie M 0 FIi 0
也称为质点系的达朗贝尔原理：作用在质点系上的外 力与虚加在每个质点上的惯性力在形式上组成平衡力系。
平面任意力系：
Fixe FIix 0 Fiye FIiy 0
质点系的达朗贝尔原理：质点系中每个质点上作用的
主动力，约束力和它的惯性力在形式上组成平衡力系。
记 Fi(e) 为作用于第i个质点上外力的合力。
Fi (i) 为作用于第i个质点上内力的合力。
则有
Fi e Fi i FIi 0
M0 Fie
M 0 Fi i
M 0 FIi 0
求：轮缘横载面的张力(不计辐条受力)。
解：FIi
mi ain
m
2R
RiR 2
Fx 0, FIi cos FA 0
Fy 0, FIi sin FB 0
令 i 0,
FA
2
m
R 2 cos
0 2
d
mR 2
2
FB
2
m R 2 sin
0 2
d
mR 2 2
§ 13-3 刚体惯性力系的简化
v
FT l sin 2
m
2.1m s
例 列车在水平轨道上行驶，车厢内悬挂一单摆， 当车厢向右作匀加速运动时，单摆左偏角度α ， 相对于车厢静止。求车厢的加速度a。
选单摆的摆锤为研究对象 虚加惯性力
FI = ma
由动静法，有
ΣFx=0
mg⋅sinα−FI cosα=0 解得 a=g⋅tgα
a=g⋅tgα
转动。
求：基础与地角螺钉 给电动机总的约束力。
解：FI m2e 2
Fx 0, Fx FI sin 0
Fy 0, Fy m1 m2 g FI cos 0
主矢： 主矩：
= −Joα （负号表示与α反向）
向铰链O简化：
例 均质杆长l ，质量m，与水平面铰接， 杆由 与水平面成ϕ0 角位置静止落下。求开始落下 时杆AB的角加速度及支座A的约束力。
选杆AB为研究对象 虚加惯性力系：（向铰链A简化）
用动力学普遍定理再求解此题：
３ 刚体作平面运动
2. 是形式上的平衡，质点实际上并不 平衡。
例 已知：m 0.1kg, l 0.3m, 60 求： v , FT .
解： FIn
man
m
l
v2 sin
mg FT FI 0
Fb 0, F1 cos mg 0
Fn 0, FT sin FIn 0
解得
FT
mg
cos
1.96N
Jean le Rond d’Alembert
（1717-1783)
达朗贝尔原理将动力学和静力学按统一的观 点来处理。它与虚位移原理一起为分析力学 的发展奠定了基础。
一位把微分看成是函数极限 的数学家
认为力学应该是数学家的主 要兴趣
第一次用微分方程表示场 偏微分方程论的创始人
Jean le Rond d’Alembert