第四章根轨迹设计

第四章根轨迹法4-1 根轨迹法的基本概念4-2 常规根轨迹的绘制法则4-3 广义根轨迹4-1 根轨迹法的基本概念一、根轨迹的概念根轨迹：系统中某个参数从零到无穷变化时，系统闭环特征根在s平面上移动的轨迹。

根指的是闭环特征根(闭环极点)。

根轨迹法是根据开环传递函数与闭环传递函数的关系，通过开环传递函数直接分析闭环特征根及系统性能的图解法。

K =0 s 1=0 s 2=-40 < K <1s 1 s 2为不等的负实根K =1s 1=-2 s 2=-21 < K < ∞s 1s2 实部均为-2由根轨迹可知：1）当K =0时,s 1=0,s 2=-1,这两点恰是开环传递函数的极点,同时也是闭环特征方程的极点.2）当0<K < 1 时,s 1,2都是负实根,随着k 的增长,s 1从s 平面的原点向左移,s 2从-1点向右移。

3) 当K = 1时, s 1,2= -2,两根重合在一起,此时系统恰好处在临界阻尼状态。

4) 1 <K <∞,s 1,2为共轭复根,它们的实部恒等于-2，虚部随着K 的增大而增大,系统此时为欠阻尼状态。

★在s平面上,用箭头标明K增大时,闭环特征根移动的方向,以数值表明某极点处的增益大小。

有了根轨迹图就可以分析系统的各种性能：(1)稳定性:根轨迹均在s的左半平面,则系统对所有K>0都是稳定的。

(2)稳态性能:如图有一个开环极点(也是闭环极点)s=0。

说明属于I型系统，阶跃作用下的稳态误差为0。

在速度信号V0t作用下,稳态误差为V0/K，在加速度信号作用下,稳态误差为∞。

(3)动态性能：过阻尼临界阻尼欠阻尼K越大，阻尼比ξ越小,超调量σ%越大。

由此可知：1、利用根轨迹可以直观的分析K的变化对系统性能的影响。

2、根据性能指标的要求可以很快确定出系统闭环特征根的位置；从而确定出可变参数的大小，便于对系统进行设计。

由以上分析知：根轨迹与系统性能之间有着密切的联系,但是,高阶方程很难求解，用直接解闭环特征根的办法来绘制根轨迹是很麻烦的。

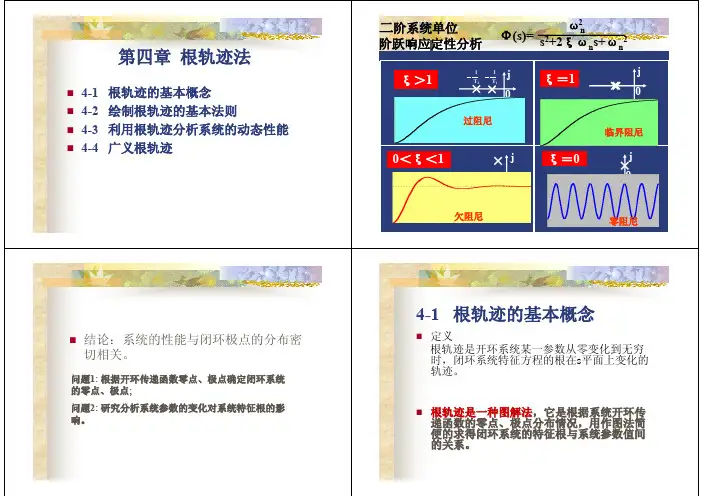
二阶系统单位第四章 根轨迹法4-1 4-2 4-3 4-4 根轨迹的基本概念 绘制根轨迹的基本法则 利用根轨迹分析系统的动态性能 广义根轨迹阶跃响应定性分析 ξ＞1 ξ＞11 12 1ω2n 2 Φ(s)= 2 s +2ξωns+ωn2j j 00 j√ 2- 1 - T ±j ωn ξξ＝1 S1,2= T ξω 0t t1 2 2 1 1 2T - T e S 过阻尼 e ξ＝1 1+ Te1,2=n+ T = -ωn h(t)= 1 -(1+ωnt) 0 -ωnt h(t)= 1 1 临界阻尼 T T ξω j0＜ξ＜1 0＜ ξ ＜ 1ξ j n - ξ2 S1,2= - ωn±j ω√1ξ＝0n0h(t)=j 0 0 j零阻尼1 √1-ξ ξ＝012S t = ±j t+β) e-ξω1,2sin(ωdωn 欠阻尼nh(t)= 1 -cosωnt 04-1 根轨迹的基本概念结论：系统的性能与闭环极点的分布密 切相关。

问题1: 根据开环传递函数零点、极点确定闭环系统 问题1: 的零点、极点; 的零点、极点; 问题2: 研究分析系统参数的变化对系统特征根的影 问题2: 响。

定义 根轨迹是开环系统某一参数从零变化到无穷 时，闭环系统特征方程的根在s平面上变化的 轨迹。

根轨迹是一种图解法，它是根据系统开环传 递函数的零点、极点分布情况，用作图法简 便的求得闭环系统的特征根与系统参数值间 的关系。

根轨迹 —— 系统性能例: 系统结构图如图所示，分析 特征根 S 随开环增益K 变化的趋势。

D( s ) = s 2 + 2 s + K * = 0解. G ( s ) =K K * = 2K = s ( 0 .5 s + 1 ) s( s + 2)K : 开环增益 * K : 根轨迹增益k * = 2ks1s2s1, 2 = −1 ± 1 − k *Φ( s ) =C ( s) K = R( s ) s 2 + 2 s + K *Re[ S1, 2 ] < 0, 系统绝对稳定*D( s ) = s 2 + 2 s + K * = 0s1, 2 = −1 ± 1 − k *b0 s m + b1s m −1 + Λ + bm −1s + bm M ( s ) = G(s) H (s) = a0 s n + a1s n −1 + Λ + an −1s + an D( s)K * ( s − z1 )Λ ( s − z m ) = ( s − p1 )( s − p2 )Λ ( s − pn ) K * ∏ ( s − zi )i =1 mG( s) Φ( s ) = 1 + G( s)H ( s)G( s) H ( s) =∏ (s − p )j =1 jn2 K (τ 1s + 1) Λ (τ 2 s 2 + 2ξ1τ 2 s + 1)... G(s) H (s) = v s (T1s + 1) Λ (T22 s 2 + 2ξ 2T2 s + 1)...K = K*∏ ∏j =1 i =1 nmzi pj根轨迹方程一般情况下K * ( s − z1 ) Λ ( s − z m ) G( s) H ( s) = = ( s − p1 )( s − p2 )Λ ( s − pn ) K * ∏ ( s − zi )i =1m nG( s) H ( s) =mK s − z1 Λ s − z m = K* s − p1 s − p2 Λ s − pn*∏ (s − z ) ∏ (s − p )j =1 j i =1 n im=1∏ (s − p )j =1 jn∠G( s ) H ( s ) = ∑ ∠( s − zi ) − ∑ ∠( s − p j ) = ( 2k + 1)πi =1 j =1Φ( s ) =G( s) 1 + G( s) H ( s)1. s平面上满足相角条件的点（必定满足幅值条件） 一 定在根轨迹上。