第四章根轨迹

第四章：根轨迹法第四章根轨迹法本章⽬录4.1 根轨迹的⼀般概念4.2 绘制根轨迹的数学依据及其性质4.3 绘制根轨迹的⼀般规则4.4 *绘制根轨迹的MATLAB函数介绍4.5 例题4.6 参数根轨迹和多回路系统的根轨迹4.7 正反馈回路和⾮最⼩相位系统根轨迹——零度根轨迹⼩结本章简介从前章得知闭环极点在根平⾯上的分布，反映着系统的固有性能。

故为了获得较好性能，就希望极点在根平⾯上有较好的分布。

亦即，为了研究系统的动态性能，就可以通过闭环极点在根平⾯上的分布来进⾏。

闭环极点是系统特征⽅程的根sb。

若其特征⽅程中，各系数变化，则⽆疑，其根sb也在变化。

各系数的变化往往相应着系统的许多实际参数的变化⽽形成。

在根迹中，⼀般总是以增益 (当然也可其它参数,如时间常数 )的变化⽽导致各系数的变化,即sb的变化。

如果连续变化,则sb也连续变化。

相应于由0连续变化到∞时, sb在根平⾯上的连续变化⽽形成的轨迹,即闭环系统特征根的根轨迹--若⼲条曲线。

这样,相应于各个值下的闭环极点在根平⾯上的分布就⼀⽬了然了。

这对系统的分析、设计带来了极⼤的⽅便.。

所谓根轨迹法，就是⽤图解的⽅法确定出闭环特征根的⼀种⽅法。

先在复数平⾯上画出系统某⼀参数的全部数值下的特征⽅程的所有根，即根轨迹。

然后⽤图解的⽅法确定出该参数某⼀特定数值时的闭环特征根。

从⽽分析出系统所具有的性能。

或反之，在根迹上先确定出符合系统性能要求的闭环特征根。

从⽽⽤图解的⽅法求出相应的系统应具有的参数值。

相对时域法，很直观，且避免了求解系统⾼阶特征⽅程的困难。

现在计算机科学有了飞速发展，特别是MATLAB语⾔及其相应⼯具箱，有强⼤的数值计算和图形绘制功能。

所以利⽤MATLAB语⾔相关函数绘制系统根迹及求根等均是轻⽽易举的事。

这就给根迹法的应⽤开辟了更好的前景。

本章在介绍传统的根轨迹法及其⽰例的同时，有机结合介绍MATLAB语⾔相关的根轨迹函数及相应⽰例的解题程序。

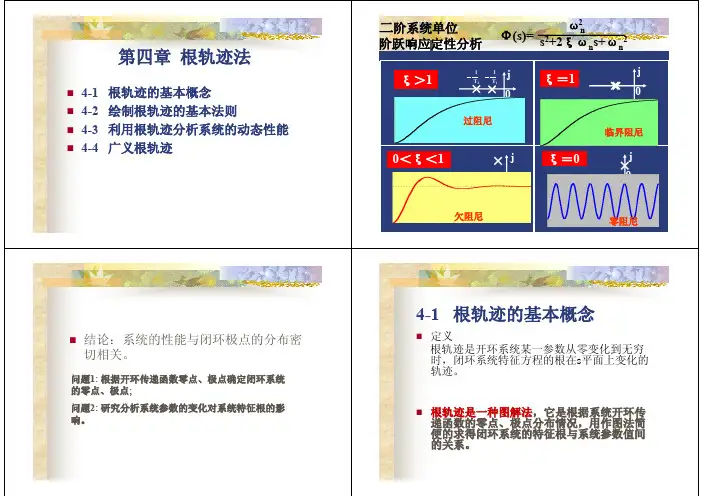
二阶系统单位第四章 根轨迹法4-1 4-2 4-3 4-4 根轨迹的基本概念 绘制根轨迹的基本法则 利用根轨迹分析系统的动态性能 广义根轨迹阶跃响应定性分析 ξ＞1 ξ＞11 12 1ω2n 2 Φ(s)= 2 s +2ξωns+ωn2j j 00 j√ 2- 1 - T ±j ωn ξξ＝1 S1,2= T ξω 0t t1 2 2 1 1 2T - T e S 过阻尼 e ξ＝1 1+ Te1,2=n+ T = -ωn h(t)= 1 -(1+ωnt) 0 -ωnt h(t)= 1 1 临界阻尼 T T ξω j0＜ξ＜1 0＜ ξ ＜ 1ξ j n - ξ2 S1,2= - ωn±j ω√1ξ＝0n0h(t)=j 0 0 j零阻尼1 √1-ξ ξ＝012S t = ±j t+β) e-ξω1,2sin(ωdωn 欠阻尼nh(t)= 1 -cosωnt 04-1 根轨迹的基本概念结论：系统的性能与闭环极点的分布密 切相关。

问题1: 根据开环传递函数零点、极点确定闭环系统 问题1: 的零点、极点; 的零点、极点; 问题2: 研究分析系统参数的变化对系统特征根的影 问题2: 响。

定义 根轨迹是开环系统某一参数从零变化到无穷 时，闭环系统特征方程的根在s平面上变化的 轨迹。

根轨迹是一种图解法，它是根据系统开环传 递函数的零点、极点分布情况，用作图法简 便的求得闭环系统的特征根与系统参数值间 的关系。

根轨迹 —— 系统性能例: 系统结构图如图所示，分析 特征根 S 随开环增益K 变化的趋势。

D( s ) = s 2 + 2 s + K * = 0解. G ( s ) =K K * = 2K = s ( 0 .5 s + 1 ) s( s + 2)K : 开环增益 * K : 根轨迹增益k * = 2ks1s2s1, 2 = −1 ± 1 − k *Φ( s ) =C ( s) K = R( s ) s 2 + 2 s + K *Re[ S1, 2 ] < 0, 系统绝对稳定*D( s ) = s 2 + 2 s + K * = 0s1, 2 = −1 ± 1 − k *b0 s m + b1s m −1 + Λ + bm −1s + bm M ( s ) = G(s) H (s) = a0 s n + a1s n −1 + Λ + an −1s + an D( s)K * ( s − z1 )Λ ( s − z m ) = ( s − p1 )( s − p2 )Λ ( s − pn ) K * ∏ ( s − zi )i =1 mG( s) Φ( s ) = 1 + G( s)H ( s)G( s) H ( s) =∏ (s − p )j =1 jn2 K (τ 1s + 1) Λ (τ 2 s 2 + 2ξ1τ 2 s + 1)... G(s) H (s) = v s (T1s + 1) Λ (T22 s 2 + 2ξ 2T2 s + 1)...K = K*∏ ∏j =1 i =1 nmzi pj根轨迹方程一般情况下K * ( s − z1 ) Λ ( s − z m ) G( s) H ( s) = = ( s − p1 )( s − p2 )Λ ( s − pn ) K * ∏ ( s − zi )i =1m nG( s) H ( s) =mK s − z1 Λ s − z m = K* s − p1 s − p2 Λ s − pn*∏ (s − z ) ∏ (s − p )j =1 j i =1 n im=1∏ (s − p )j =1 jn∠G( s ) H ( s ) = ∑ ∠( s − zi ) − ∑ ∠( s − p j ) = ( 2k + 1)πi =1 j =1Φ( s ) =G( s) 1 + G( s) H ( s)1. s平面上满足相角条件的点（必定满足幅值条件） 一 定在根轨迹上。