线性电路基本定理

电路基本定律基尔霍夫定律
基尔霍夫定律是电路中电压和电流所遵循的基本规律，是分析和计算较为复杂电路的基础，1845年由德国物理学家G.R.基尔霍夫提出。

基尔霍夫（电路）定律包括基尔霍夫电流定律（KCL）和基尔霍夫电压定律（KVL）。

基尔霍夫（电路）定律既可以用于直流电路的分析，也可以用于交流电路的分析，还可以用于含有电子元件的非线性电路的分析。

基尔霍夫定律建立在电荷守恒定律、欧姆定律及电压环路定理的基础之上，在稳恒电流条件下严格成立。

当基尔霍夫第一、第二方程组联合使用时，可正确迅速地计算出电路中各支路的电流值。

由于似稳电流(低频交流电) 具有的电磁波长远大于电路的尺度，所以它在电路中每一瞬间的电流与电压均能在足够好的程度上满足基尔霍夫定律。

因此，基尔霍夫定律的应用范围亦可扩展到交流电路之中。

3.3 叠加原理1．定义叠加原理是线性电路的基本定理。

在线性电路中，任何一个支路的电流和电压，均是由电路中各个电源单独作用时，在此支路产生电流及电压的代数和。

2．解题思路用叠加原理解决电路问题的实质，是把含多个电源的复杂电路分解为多个简单电路的叠加。

应用时要注意两个问题：一是某电源单独作用时，其他电源的处理方法；二是叠加时各分量的方向问题。

以上问题的解决方法请看应用举例。

3．适用范围在多个电源作用的电路中，仅研究一个电源对多支路或多个电源对一条支路的影响的问题。

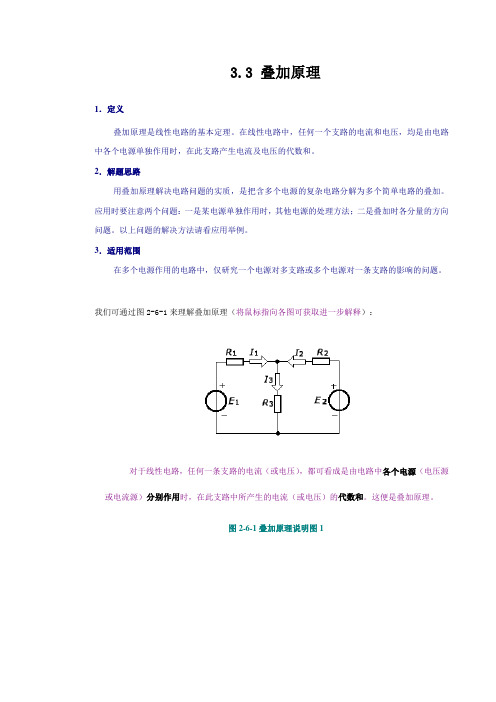
我们可通过图2-6-1来理解叠加原理（将鼠标指向各图可获取进一步解释）：对于线性电路，任何一条支路的电流（或电压），都可看成是由电路中各个电源（电压源或电流源）分别作用时，在此支路中所产生的电流（或电压）的代数和。

这便是叠加原理。

图2-6-1叠加原理说明图1图2-6-2叠加原理说明图1图2-6-3叠加原理说明图1在图2-6-1中，我们假定要求电流I1。

直接对图2-4-1求解，其值如下：(2-6-1)显然，图2-6-1为线性电路，考虑电源E1单独作用的电路：将电压源E2短路，电路如图2-6-2。

求解电路，有：考虑电源E2单独作用的电路：将电压源E1短路，电路如图2-6-3。

求解电路，有：分析式(2-6-1)，I1为I1′、I1″两部分的代数和，这便是叠加原理的含义。

用叠加原理求解电路的解题步骤如下：（1）分析电路，选取一个电源，将电路中其它所有的电流源开路，电压源短路，画出相应电路图，并根据电源方向设定待求支路的参考电压或电流方向；（2）重复步骤（1），对N个电源画出N个电路；（3）分别对N个电源单独作用的N个电路计算待求支路的电压或电流；（4）应用叠加原理，计算最终结果。

基本电路定律与定理电路是电子工程中的基础概念，了解和掌握基本电路定律与定理是学习电子工程的关键。

本文将介绍几个基本电路定律与定理，包括欧姆定律、基尔霍夫定律和叠加定理。

通过对这些定律与定理的理解和应用，能够更好地分析和设计电路。

一、欧姆定律欧姆定律是描述电路中电流、电压和电阻之间关系的基本定律。

根据欧姆定律，电流I等于通过电阻R的电压V与电阻R之间的比值，即I=V/R。

这个关系可以用一个简单的公式来表示，为电流等于电压除以电阻。

欧姆定律的应用非常广泛，例如在电路设计中可以通过欧姆定律计算电阻的大小，也可以通过欧姆定律计算电路中的电流和电压。

欧姆定律为电子工程师提供了分析和解决电路问题的基本方法。

二、基尔霍夫定律基尔霍夫定律是描述电路中电流和电压分布关系的定律。

基尔霍夫定律包括电流定律和电压定律两个方面。

1. 电流定律基尔霍夫电流定律（KCL）指出，在电路中任意节点处，所有流入节点的电流之和等于所有流出节点的电流之和。

这可以表示为∑Iin =∑Iout。

基尔霍夫电流定律是基于电荷守恒原理的，根据该定律，电流在电路中的分布和流动可以得到合理的解释。

2. 电压定律基尔霍夫电压定律（KVL）指出，沿着任何一个闭合回路，电压的代数和等于零。

这可以表示为∑V = 0。

基尔霍夫电压定律是基于能量守恒原理的，通过这个定律可以更好地理解电压在电路中的变化和分布情况。

基尔霍夫定律在电路分析和设计中具有重要的作用，可以帮助工程师解决复杂电路中的电流和电压分布问题。

三、叠加定理叠加定理是用来求解复杂电路中电流和电压的重要方法。

叠加定理的基本思想是将复杂电路分解成若干简化的小电路，分别计算每个小电路中的电流和电压，然后将它们叠加得到最终的结果。

叠加定理适用于线性电路，通过将各个源依次置零来计算小电路的电流和电压，所得到的结果叠加即可得到整个电路的电流和电压。

叠加定理是电路分析中的一种重要方法，可以简化复杂电路的计算过程，提高计算效率。

第2章 线性电阻电路的分析内容：网络方程法：支路电流法、节点电压法、回路电流法。

线性电路定理：替代定理、戴维宁定理、诺顿定理。

2.1 电阻的串联、并联和混联电路分析线性电阻电路的方法很多，但基本依据是KCL 、KVL 及元件的伏安关系()VAR 。

根据这些基本依据可推导出三种不同的分析电路的方法：等效法、方程法、定理法。

本章首先介绍等效变换，然后讨论支路电流法、网孔分析法及节点电位法，最后介绍常用定理，包括叠加定理和齐次定理、戴维南定理和诺顿定理等。

2.1.1 电路等效的一般概念1．等效电路的概念：在分析电路时，可以用简单的等效电路代替结构较复杂的电路，从而简化电路的分析计算，它是电路分析中常用的分析方法。

但值得注意的是，等效电路只是它们对外的作用等效，一般两个电路内部具有不同的结构，工作情况也不相同，因此，等效电路的等效只对外不对内。

2．等效电路的应用：简化电路。

2.1.2 电阻的串联、并联与混联1. 电阻的串联电阻串联的概念：两个或两个以上电阻首尾相联，中间没有分支，各电阻流过同一电流的连接方式，称为电阻的串联。

串联电阻值： 123R R R R =++ 电阻串联时电流相等，各电阻上的电压：1 11122223333RUU IR R UR RRUU IR R UR RRUU IR R UR R⎫===⎪⎪⎪===⎬⎪⎪===⎪⎭2. 电阻的并联电阻的并联概念：两个或两个以上电阻的首尾两端分别连接在两个节点上，每个电阻两端的电压都相同的连接方式，称为电阻的并联并联电阻电流值：123123123111U U UI I I I UR R R R R R⎧⎫=++=++=++⎨⎬⎩⎭并联电阻值：1231111R R R R=++电阻并联电路的等效电阻的倒数等于各个电阻的倒数之和。

电阻并联时电压相等，各电阻上的电流：111122223333GU RII IR R GGU RII IR R GGU RII IR R G⎫===⎪⎪⎪⎪===⎬⎪⎪===⎪⎪⎭3. 电阻的混联既有电阻串联又有电阻并联的电路叫混联电路。

电路中的戴维南定理电路理论是电子工程中最基本的概念之一，而要理解电路理论的关键是掌握戴维南定理，这是电路中的基本定理之一。

戴维南定理是一种线性电路分析方法，可以用于求解任何一个线性电路中的电流，电压和电阻等参数。

该定理可以帮助电子工程师更好地设计和分析各种电路，例如放大器，滤波器，稳压器和模拟电路等。

戴维南定理被广泛地应用于各种电路分析问题中，特别是在解决交流电路的问题中非常有效。

下面将简要介绍戴维南定理的概念，其含义和应用。

戴维南定理的概念在电路中，戴维南定理将电路分为两个部分：与目标电阻并联的电路和与目标电阻串联的电路。

根据戴维南定理，可以用任一一种方法求解电路中的电流、电压或电阻等参数，求解结果相同。

与目标电阻并联的电路称为等效阻抗电路，与目标电阻串联的电路称为等效电压电路。

戴维南定理的含义戴维南定理告诉我们，一个电路可以被表示为两个等效电路，一个是与目标电阻在并联的等效电路，另一个是与目标电阻在串联的等效电路。

这意味着，在求解电路参数时，我们可以选择任意一个等效电路进行计算，求解结果是相同的。

此外，戴维南定理还规定了计算等效电路所需元件的数值。

这些元件的计算方法是将目标电阻添加到电路中，并根据电路参数计算得出。

戴维南定理的应用戴维南定理可以帮助我们更有效地分析电路中的电流、电压和电阻等参数。

例如，当需要计算电路中某个元件的电流时，我们可以通过使用等效阻抗电路和基尔霍夫定律等方法来计算。

类似地，当需要计算电路中某个元素的电压时，我们可以使用等效电压电路和基尔霍夫定律等方法来计算。

此外，戴维南定理还广泛应用于解决电路分析中的复杂问题。

例如，在计算交流电路的幅值和相位时，我们可以使用戴维南定理和欧姆定律等方法，将电路简化为等效阻抗电路，然后进行计算。

总结戴维南定理是电路设计和分析中不可或缺的工具之一，它可以帮助我们更好地了解电路的工作原理和性能。

运用戴维南定理可以将电路简化为等效电路，使复杂的电路问题变得更加容易和直观。

实验二电路基本定律及定理的验证一、实验目的1、通过对KCL、KVL的验证，加深对定律的理解。

2、通过对戴维南定理、叠加定理的验证，加深对定理的理解和灵活应用。

3、明确实际测量中存在的误差，学会分析误差。

二、实验设备和器材直流可调稳压电源0～30 V万用表MF-500型实验电路板三、实验原理与说明1、基尔霍夫定律（KCL、KVL）电路中的基本定律，适用于集总参数电路。

KCL：任一时刻，任一节点，所有流出该节点的电流代数和恒为零，即∑i = 0。

KVL：任一时刻，任一回路，沿某绕行方向所有元件电压的代数和恒为零，即∑u = 0。

2、叠加定理适应线性电路中的电流、电压。

线性电路中含多个独立源时，任一支路的电流或电压是每个独立源单独作用时在该支路产生的电流或电压的代数和。

电源单独作用是指：除该电源外，其他独立源取零，即电压源短路，电流源开路，受控源不变。

3、戴维南定理适应线性含源二端网络。

任一线性含源二端网络，对外电路而言，均可用一个电压源和一个电阻串联的组合来等效——戴维南等效电路。

电压源的电压为含源二端网络的开路电压U oc；等效电阻为对应无源二端网络的等效电阻R0。

4、误差分析（1）测量值与真实值间的差异称误差。

（2）误差有两类：绝对误差=︱测量值-真实值︱相对误差= （绝对误差/ 真实值）×100﹪（3）实际测量中，应利用合理测试手段使误差最小。

四、实验内容及步骤实验电路图如实验图2-1所示。

1、KCL 、KVL 的验证（1）调节两个直流电源，使一个为8V 作为U1接入AB 端，另一个为4V 作为U2接入A ’B ’两端；（2）节点O 处接通，测量I 1、I 2、I 3并填入实验表2-1中；（3）用AOO ’B ’回路，分别测电压U AO 、O O 'U 、B O 'U 、U BA 填入实验表2-1中； （4）验证∑U = U AO +O O 'U +B O 'U + U BA = 0，∑I =I 1 + I 2 + I 3 = 0。