用旋转矢量描述波形及振动曲线与波形的转换

旋转矢量法求合振动方程旋转矢量法是一种常用的工具，用于求解多个振动体的合振动方程。

它在振动学、固体力学、流体力学等领域中都有广泛的应用。

本文将从基本原理、数学推导、具体应用等方面进行阐述。

1. 基本原理旋转矢量法是建立在以下假设基础上的：对于任意振动体，其振动可以看作是由平动和转动两部分构成的，其中平动由质心偏离平衡位置造成，而转动则由振动体绕其质心旋转所引起的。

因此，我们可以将振动体的质心看作是一个之间相邻关联的旋转矢量，从而求得其合振动方程。

2. 数学推导首先，我们需要确定旋转矢量的表达式。

假设一个振动体的质心在平衡位置处的坐标为$(x,y,z)$，而其受到的外力为$\boldsymbol F$。

则该振动体所受的旋转矢量$\boldsymbol A$可表示为：$$\begin{aligned}\boldsymbol A &= \boldsymbol r \times \boldsymbol F\\ &= \begin{vmatrix}\boldsymbol e_x & \boldsymbol e_y & \boldsymbol e_z\\x-x_0 & y-y_0 & z-z_0 \\F_x & F_y & F_z\end{vmatrix}\\&= (y-y_0)F_z\boldsymbol e_x + (z-z_0)F_x\boldsymbole_y + (x-x_0)F_y\boldsymbol e_z\end{aligned}$$其中，$\boldsymbol r=(x-x_0)\boldsymbol e_x+(y-y_0)\boldsymbol e_y+(z-z_0)\boldsymbol e_z$为振动体的位置矢量，$\boldsymbol e_x,\boldsymbol e_y,\boldsymbol e_z$为三个坐标轴的单位矢量，$x_0,y_0,z_0$为平衡位置的坐标。

简谐振动的旋转矢量法
简谐振动的旋转矢量法（also known as the rotational vector method）是一种描述简谐振动运动的方法。

这种方法将简谐振动的位移表示为一个旋转矢量，该旋转矢量的大小和方向都随时间变化。

在这种方法中，假设物体在振动过程中绕一个固定轴旋转。

这个固定轴被称为挠度轴，它垂直于振动平面。

振动的位移被表示为从挠度轴指向物体的矢量。

根据简谐振动的性质，位移矢量旋转的角度随时间变化，而角度的变化速率与振动频率相关。

通过将位置矢量的旋转速率与振动频率相关联，可以得到简谐振动的动态方程。

旋转矢量法可以应用于各种简谐振动问题，包括简谐振子、摆线振动等。

通过使用该方法，可以更轻松地分析和计算简谐振动的运动特性，例如位移、速度和加速度等。

此外，该方法还可以用于解决相关问题，如相位差和共振等。

总的来说，简谐振动的旋转矢量法是一种较为直观和简便的分析简谐振动运动的方法，它通过描述位移矢量的旋转来描述振动过程，并可以得到简谐振动的动态方程。

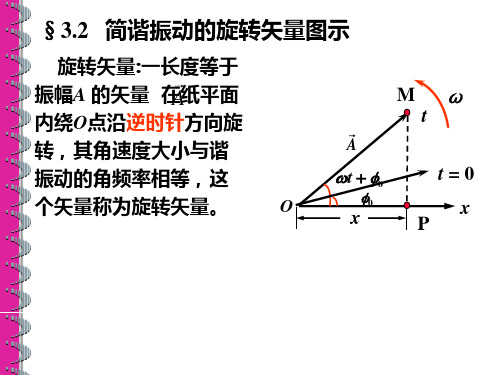
用旋转矢量描述波形及振动曲线与波形的转换杨庆怡;刘奕新;郭进【摘要】类比于简谐振动的旋转矢量描述法, 提出用波动旋转矢量描述波形以及利用振动旋转矢量和波动旋转矢量来实现振动曲线与波形之间相互转换的方法.【期刊名称】《广西科学院学报》【年(卷),期】2010(026)002【总页数】4页(P107-109,115)【关键词】振动曲线;波形;旋转矢量;转换【作者】杨庆怡;刘奕新;郭进【作者单位】广西大学物理科学与工程技术学院,广西南宁,530004;广西大学物理科学与工程技术学院,广西南宁,530004;广西大学物理科学与工程技术学院,广西南宁,530004【正文语种】中文【中图分类】O321Abstract:By comparing w ith harmonic vibration described using the rotation vectorAt,thewave rotating vectorAxwas introduced to describe wave form.A method to realize the transformation between the harmonic vibration curve and the wave form w ith rotation vectorAtwas proposed. Key words:harmonic vibration curve,wave form,rotatingvectors,transformation振动与波是大学物理课程中的基本内容,振动是单一质元在线性回复力的作用下在其平衡位置附近作往复运动的过程;波动则是弹性媒质在弹性力的作用下,由于波源的振动而引起媒质质元从波源开始由里向外依次发生振动的过程.简谐振动和平面简谐波是振动和波动过程中最为简单的情形.振动曲线与波形之间的相互转换是学习振动与波内容时经常遇到的问题,在由x0处质元的振动曲线求时刻的t0波形时,需要考虑该质元的相位、振动方向以及与相邻质元间的相位关系,在明确这些因素之后,即可根据质元的振动曲线作出相应的波形;在由t0的波形求x0处质元振动曲线时,需要根据该时刻的波形确定x0处质元的相位、位移以及振动方向,在明确这些因素之后,即可作出该质元的振动曲线.然而,在大学物理课程的教学过程中,学生在学习了相关的知识之后,并不一定能够熟悉地了解振动过程与波动过程的本质,对振动过程中质元的相位、相位变化以及振动方向和波动过程中质元的位移、振动方向以及质元间的相位关系理解不透彻,从而不能顺利而正确地进行转换.因此,提出一种较为直观的方法可以使学生在学习振动与波的内容时能够更好地掌握振动曲线与波形的转换.类比于简谐振动的旋转矢量描述法,本文提出用波动旋转矢量描述波形以及利用振动旋转矢量和波动旋转矢量来实现振动曲线与波形之间相互转换的方法. 在线性回复力的作用下质元作往复运动时的位移y与时刻t满足的振动称为简谐振动,其中,A为振幅,(ωt+ φ0)为时刻的相位,φ0为初相位.利用(1)式可以求出质元作简谐振动时的速度v和加速度a,由(1)式描述的简谐振动可以用旋转矢量(称为振动旋转矢量)来描述.如图1所示,大小保持不变的矢量At以其始端O为定点以角速度ω沿逆时针方向转动,在初始时刻At与y轴的夹角为φ0,则在时刻t时At与y轴的夹角为(ωt+φ0),则At的终端M在y轴上的投影P为y=Acos(ωt+φ0),从而可以用这样一个旋转矢量来描述质元的简谐振动.利用振动旋转矢量来描述简谐振动的优点是可以方便地作出振动曲线以及直观地了解质元作简谐振动时的相位、位移以及质元的运动方向.根据质元作简谐振动时的速度和加速度,类比于振动旋转矢量描述简谐振动的位移,可以引入速度旋转矢量和加速度旋转矢量来描述简谐振动过程中质元的速度和加速度随时间变化的关系[1].波动的实质是媒质在弹性力的作用下,由于波源的振动引起媒质中一系列的质元从波源开始由里向外先后作简谐振动,描述波源以及所有参与振动的质元振动规律的方程称为波动方程,它反映了波源以及所有参与振动的质元集体作不同步的简谐振动.平面简谐横波的波动方程为其中,“∓”号分别表示波沿x轴正向传播和负向传播,[ω(t∓x/u)+φ0]为x处的质元在时刻t的相位,φ0为坐标原点处质元的初相位,u为波的传播速度.当给定x=x0时(4)式描述的是x0处的质元随时间作简谐振动;当给定t=t0时(4)式描述的是波源以及所有参与振动的质元在时刻t0时的位移,即波形;而当x和t都发生变化时(4)式描述的是所有参与振动的质元的振动规律(即波形随时间的变化),从波形的变化关系来看波形沿波的传播方向移动,因此称为行波.根据(4)式,对于给定的时刻t0波动方程描述的是这一时刻的波形其中,为x= 0处的质元在t0时刻的相位.在用振动旋转矢量描述简谐振动时,At以角速度ω沿逆时针方向转动,在At转动过程中,相位(ωt+φ0)随时间而增大.考虑由(5)式描述的波形,当波沿x轴正向传播时,质元的相位随坐标x而减小,当波沿x轴负向传播时,质元的相位随坐标x而增大;而相距一个波长的两个质元的相位差为2π.根据波形中质元的相位特征以及类比于用振动旋转矢量描述简谐振动,可以引入另一个旋转矢量(称为波动旋转矢量)来描述波动过程中某一时刻的波形[2].如图2所示,大小保持不变的矢量Ax以其始端O为定点以角速度ω转动,在时刻t0,坐标原点处Ax与y轴的夹角为φ′0= ωt0+ φ0,则在Ax的转动过程中,Ax与y 轴的夹角为[∓ (ω/u)x+φ′0],取负号时相位减小,表示Ax沿顺时针方向转动,而取正号时相位增大,表示Ax沿逆时针方向转动.利用关系Δφ = (ω/u)Δx=ωΔt,当Ax旋转一周时,Ax的终端M在y轴上的投影随坐标x的变化即为(5)式描述的在时刻t0时一个周期内的波形,其中,Ax沿顺时针方向转动时得到的是沿x正向传播的波形,而Ax沿逆时针方向转动时得到的是沿x负向传播的波形.通过对振动方程与波动方程的相位以及相位变化的关系进行分析,我们利用旋转矢量法来实现振动曲线与波形之间的相互转换.在振动方程(1)中,质元作简谐振动的相位(ωt+ φ0)随时间而增大,而在波动方程(4)中,对于给定的时刻t0,[ω(t0∓x/u)+φ0]描述了所有参与振动的质元的相位随坐标x变化的关系,当波沿x轴正向传播时,相位随x的增大而减小,而当波沿x轴负向传播时,相位随x的增大而增大.而从振动过程中质元的相位(ωt+ φ0)与波动过程中质元的相位[ω(t-x/u)+ φ0]来看,简谐振动在时刻t0的相位刚好就是该时刻的波形中处于坐标原点处的质元的相位.根据对振动过程和波动过程的相位及变化关系的分析,结合振动曲线和波形的旋转矢量描述方法,可以总结出利用旋转矢量法来描述振动曲线与波形间相互转换的一种便捷而可靠的方法。

旋转矢量求波动方程初相位波动方程是描述波动传播的数学模型，在物理学中有着广泛的应用。

而确定波动方程的初相位，也就是波动的起始状态，对于理解波动的性质和特点起着重要的作用。

在研究波动方程的初相位之前，我们先了解一下什么是旋转矢量。

旋转矢量是指在空间中旋转方向和角度都确定的向量，它可以用来表示物体在空间中的旋转状态。

在电磁波的研究中，旋转矢量常常用来描述电磁波的偏振状态。

当电磁波传播时，光束中的光子会随着波动的传播而发生旋转。

这种旋转可以用旋转矢量来描述，它的大小和方向表示了波动的相位和偏振方向。

因此，确定波动方程的初相位就是确定旋转矢量的大小和方向。

在确定波动方程的初相位时，我们可以通过将电磁波的传播方向与垂直方向的夹角来确定旋转矢量的方向。

而旋转矢量的大小可以根据波动的振幅来确定。

波动的振幅表示了波动的强度，它越大，表示波动的能量越强。

除了振幅和传播方向外，确定波动方程的初相位还与波动的频率有关。

频率表示了波动的周期性，它与波长之间有一个固定的关系。

我们可以通过波动的频率来确定旋转矢量的速度，从而确定初相位。

总结起来，确定波动方程的初相位需要考虑波动的振幅、传播方向和频率。

通过将电磁波的传播方向与垂直方向的夹角确定旋转矢量的方向，再根据波动的振幅和频率确定旋转矢量的大小和速度，就可以确定波动方程的初相位。

确定波动方程的初相位对于研究波动的行为和性质具有重要的意义。

它可以帮助我们理解波动的传播机制以及与其相关的物理现象。

在实际应用中，通过确定波动方程的初相位，我们可以更好地控制和调整波动的特性，为光通信、雷达、医学成像等领域的技术发展提供有力支持。

通过对旋转矢量和波动方程初相位的探讨，我们可以更深入地理解波动现象的本质和特点。

这不仅是对物理学的研究有着重要的指导意义，也是为我们更好地理解和应用波动方程提供了有力的支撑。

我们期待在未来的研究中，能够进一步深化对波动方程初相位的认识，以推动科学技术的进步和发展。

旋转矢量求波动方程初相位旋转矢量在波动方程中的初相位在波动方程中，初相位是指波动现象在某一时刻的相位状态。

相位是描述波动的重要参数，它与波动的频率和周期密切相关。

而在求解波动方程时，旋转矢量是一种常用的数学工具，可以帮助我们求得波动的初相位。

我们先了解一下旋转矢量的基本概念。

旋转矢量是指在平面或空间中绕一个固定点旋转的矢量。

它由旋转轴和旋转角度组成，可以用来表示旋转的方向和幅度。

在波动现象中，我们可以将旋转矢量应用到波的初相位的求解中。

假设我们有一个波动方程，形式为y(x, t) = A*sin(kx - ωt + φ)，其中A为振幅，k为波数，ω为角频率，φ为初相位。

我们可以将波动方程中的初相位表示为一个旋转矢量的形式，即φ = kx - ωt。

在求解波动方程时，我们常常需要确定波的初相位。

通过旋转矢量的方法，我们可以简化求解初相位的过程。

具体的方法如下：我们可以选取一个参考点作为旋转轴，通常选择波动的起点或者某一特定点作为参考点。

然后，我们需要确定旋转矢量的旋转角度。

旋转角度可以通过波动方程中的波数k和角频率ω来确定。

根据旋转矢量的定义，旋转角度等于旋转矢量在单位时间内绕旋转轴旋转的角度。

对于波动方程来说，旋转角度等于k乘以单位时间t。

因此，旋转角度可以表示为θ = k*t。

在确定了旋转轴和旋转角度后，我们就可以得到波的初相位。

根据旋转矢量的定义，初相位等于旋转矢量在初始时刻的角度。

对于波动方程来说，初始时刻的角度等于旋转角度在初始时刻t=0时的值。

因此，初相位可以表示为φ = k*x - ω*0 = k*x。

通过旋转矢量的方法，我们可以简化求解波的初相位的过程。

只需要确定旋转轴、旋转角度和初始时刻的值，就可以得到波的初相位。

这种方法不仅简单方便，而且可以通过旋转矢量的几何意义更直观地理解波的初相位。

总结起来，旋转矢量在波动方程中可以用来求解波的初相位。

通过确定旋转轴、旋转角度和初始时刻的值，我们可以得到波的初相位。