机械原理(双语)第三章lecture3-1&2

格式：ppt
大小：1.19 MB
文档页数：57

下载文档原格式

机械原理课后答案第3章

3—1 何谓速度瞬心?相对瞬心与绝对瞬心有何异同点?答：参考教材30~31页。

3—2 何谓三心定理?何种情况下的瞬心需用三心定理来确定?答：参考教材31页。

3-3试求图示各机构在图示位置时全部瞬心的位置(用符号P ，，直接标注在图上) (a)(b)答：答：（10分）(d)（10分）3-4标出图示的齿轮一连杆组合机构中所有瞬心，并用瞬心法求齿轮1ω1/ω3。

答：1)瞬新的数目：K=N(N-1)/2=6(6-1)/2=152)为求ω1/ω3需求3个瞬心P 16、P 36、P 13的位置3）ω1/ω3= P 36P 13/P 16P 13=DK/AK由构件1、3在K 点的速度方向相同，可知ω3与ω1同向。

3-6在图示的四杆机构中，L AB =60mm ，L CD =90mm,L AD =L BC =120mm, ω2=10rad/s,试用瞬心法求：1)当φ=165°时，点的速度vc ；2)当φ=165°时，构件3的BC 线上速度最小的一点E 的位置及速度的大小；3)当V C =0时，φ角之值(有两个解)。

解：1）以选定的比例尺μ机械运动简图（图b ）2）求vc 定出瞬心p12的位置（图b ）因p 13为构件3的绝对瞬心，则有ω3=v B /lBp 13=ω2l AB /μ=10××78=(rad/s)v c =μc p 13ω3=×52×=(m/s)3)定出构件3的BC 线上速度最小的点E 的位置,因BC 线上速度最小的点必与p13点的距离最近，故丛p13引BC线的垂线交于点E，由图可得v E=μω3=××=(m/s)4)定出vc=0时机构的两个位置（图c）量出φ1=°φ2=°3-8机构中，设已知构件的尺寸及点B的速度v B(即速度矢量pb)，试作出各机构在图示位置时的速度多边形。

答：（10分）（b）答：答：3—11 速度多边形和加速度多边彤有哪些特性?试标出图中的方向。

西北工大版机械原理第3章平面机构的运动分析精品PPT课件

特点：
①该点涉及两个构件。
②绝对速度相同，相对速度为零。
③相对回转中心。 2）瞬心数目若机构中有n个构件，则
P13
1 23
∵每两个构件就有一个瞬心
P12 P23
∴根据排列组合有
构件数 4 瞬心数 6
56
8
10 15 28
二、机构中瞬心的数目
若机构中有N个构件（包括机架），则
∵每两个构件就有一个瞬心
B A
E HE
1.位置分析 ①确定机构的位置（位形），绘制机构位置图。 ②确定构件的运动空间，判断是否发生干涉。
③确定构件(活塞)行程，找出上下极限位置。 ④确定点的轨迹（连杆曲线），如鹤式吊。
2.速度分析 ①通过分析，了解从动件的速度变化规律是否满足工作要求。如牛头刨 ②为加速度分析作准备。
∴根据排列组合有
K
C
2 N
N ( N 1) 2
三、机构中瞬心位置的确定
1. 通过运动副直接相联的两构件的瞬心位置确定
1）以转动副相联的两构件的瞬心
2）以移动副相联的两构件的瞬心
——转动副的中心。 P12
——移动副导路的垂直方向上的
1
1
2
无穷远处。
P12 ∞ 2
3）以平面高副相联的两构件的瞬心
3.加速度分析的目的是为确定惯性力作准备。
方法：图解法－简单、直观、精度低、求系列位置时繁琐。解析法－正好与以上相反。
实验法－试凑法，配合连杆曲线图册，用于解决实现预定轨迹问题。
3-2 用速度瞬心作平面机构的速度分析
一、速度瞬心(Instantaneous Center of Velocity——ICV) 速度瞬心(瞬心): 瞬时转动中心

机械原理第3章3[1].3

b3
d
已知：图示机构各构件的尺寸、位置及角速度ω 已知：图示机构各构件的尺寸、位置及角速度ω1 求： ω 2、ω 3 、 α 2 、 α 3 、vD 、aD 2、加速度分析、
a B 2 = a B 1 = ω 12 l AB
D 3 C k´
ar B2B3
r k a B 2 = a n 3 + a tB 3 + a B 2 B 3 + a B 2 B 3 B
？
⊥BC
？
//BC
b3
p
取极点p，取极点，按比例尺µ v (
m /s ) 作速度图 mm
v B 3 = µ v • p b3
ω3
vB3 = l BC
v B 2 B 3 = µ v • b3 b 2
动点：动点：B2 动系：固联于3构件上动系：固联于3 静系：静系：固联于机架上
ω 2 = ?ω 3 ω =
t C
已知：机构的位置，各构件的长度及原动件角速度ω 已知：机构的位置，各构件的长度及原动件角速度ω1。求：vC，vE，aC, ，， 3、加速度分析、
n
aE, ω 2, ω 3, α 2, α 3
求aE与速度分析类同
t n t
F ω1
1 A B 2 E
C
a E = a B + a EB + a EB = a C + a EC + a EC
b´
加速度影像原理证明: 加速度影像原理证明:
a CB =
n t ( a CB ) 2 + ( a CB ) 2 = 2 (ω 2 l BC ) 2 + (α 2 l BC ) 2
= l BC

机械原理课件B第三章

从动件运动形式：
S2
a)升-停-降-停
1
t
S2
b)升-停-降
1
t
0
S2
s
h
s'
0
S2
s
h
c)升-降-停
1
t
d)升-降
1
t
0
h
s'
0
h
二、常用运动规律: 1、等速运动规律
v = c a = s = dv dt = 0 = c 1 + ct
∫vdt
边界条件:
t = 0 , s = 0;
h h + 1 < t + s + s + < ≤ 1 ≤ t + 2 2
h
3、余弦加速度运动 (简谐运动规律)
这种运动规律的加速度方程是半个周期的余弦曲线, 根据质点在圆周上作简谐运动如下图所示:
h 从动件运 (1 s2 = 2 动最高点
位移方程:
cos )
h
当瞬心点p与导路线在转轴同侧时取号当瞬心点p与导路线在转轴同侧时取号当瞬心点p与导路线在转轴异侧时取号当瞬心点p与导路线在转轴异侧时取号minmin求得值代入上式为了解决这对矛盾常min应大于轮毂半径协调一般毂的尺寸安装时要考虑基圆与轮minmin理论廓线实际廓线应将太小minmindsmaxminmin从动件转轴的轨迹圆从动件杆长机架线例题
O2 B8 B7
B5
O2( 7 )
实际廓线
O2(8 )
B6
O2(9 )
理论廓线:滚子中心的轨迹线. 实际廓线:凸轮的可见轮廓线.
滚子从动件:理论廓线与实际廓线在法

南航机械原理课件第3章-3

8
二、偏置曲柄滑块机构
在图所示的中，已知曲柄、连杆的长度l1、 l2和偏距e，原动件１以角速度ω1逆时针方向匀速转动。欲求连杆２的转角 ϕ2，角速度ω2和角加速度ε2，以及滑块Ｃ的位移ｓC，速度ｖ C和加速度ａC。 ω1 l1l1 B l2 l2 A e e C
9
1. 建立坐标系xoy； 2. 将构件或运动副的相对位置看作矢量，使其形成封闭的矢量图。得矢量方程
从上述方程可解出ϕ2和ϕ3
l cos ϕ 3 + l 4 − l1 cos ϕ 1 1 2 2 sin ϕ 2 = 3 sin ϕ 3 = (A ± B 1− A + B ) 2 l2 1+ B
式中：
l 42 − 2 l1 l 4 cos ϕ 1 + l12 + l 32 − l 22 A= 2 ( l 4 − l1 cos ϕ 1 ) l 3
请复习理论力学中的运动分析
15
cos( ϕ1 − ϕ 2 ) l1 cos 2 ϕ1 aC = l1ω12 [ + ] 3 cos ϕ 2 l 2 cos ϕ 2
12
解： 1）按比例画机构运动简图 2）进行速度分析
4 E C2,C3,C4 C 3 D 2
B
ω1
A
1
ϕ1
（1）以构件2为研究对象，B2为基点列出C2点的速度方程。（2）考虑C处的重合点。以构件3为动系，C2为动点，列出C2点的速度方程。要分析速度方程中每个量的大小和方向。按比例画速度矢量图，从图中量出未知量。用影像法求D、E点的速度。 13
从上述方程可解出ω2和ω 3
l1 sin( ϕ 1 − ϕ 3 ) ω2 = − ω1 l 2 sin( ϕ 2 − ϕ 3 )

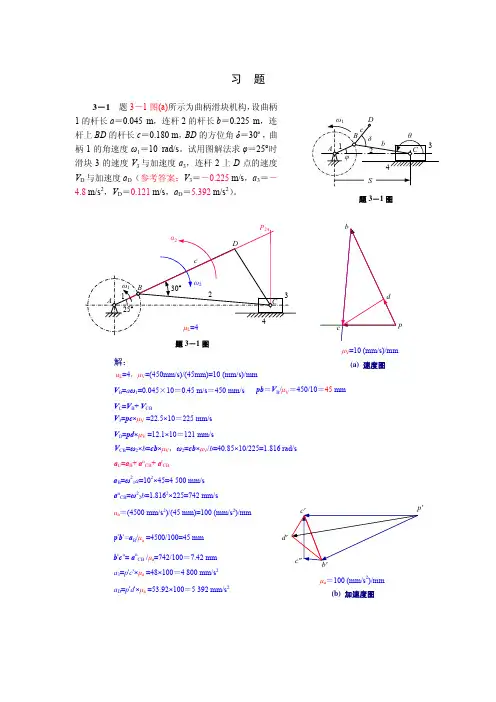
机械原理双语

题3－1图习题3－1 题3－1图(a)所示为曲柄滑块机构，设曲柄1的杆长a ＝0.045 m ，连杆2的杆长b ＝0.225 m ，连杆上BD 的杆长c ＝0.180 m ，BD 的方位角δ＝30º，曲柄1的角速度ω1＝10 rad/s 。

试用图解法求φ＝25°时滑块3的速度V 3与加速度a 3，连杆2上D 点的速度V D 与加速度a D （参考答案：V 3＝－0.225 m/s ，a 3＝－4.8 m/s 2，V D ＝0.121 m/s ，a D ＝5.392 m/s 2）。

V B =a ω1=0.045×10＝0.45 m/s ＝450 mm/s μL =4，μV =(450mm/s)/(45mm)=10 (mm/s)/mm V 3=pc ×μV =22.5×10＝225 mm/s V D =pd ×μV =12.1×10＝121 mm/spV C =V B + V CBV CB =ω2×b =cb ×μV ，ω2=cb ×μV /b =40.85×10/225=1.816 rad/s a C =a B + a n CB + a t CBa B =ω21a =102×45=4 500 mm/s a n CB =ω22b =1.8162×225=742 mm/sμa ＝(4500 mm/s 2)/(45 mm)=100 (mm/s 2)/mm b 'c "= a n CB /μa =742/100＝7.42 mm p 'b '=a B /μa =4500/100=45 mm a 3=p 'c '×μa =48×100＝4 800 mm/s 2d'a D =p 'd '×μa =53.92×100＝5 392 mm/s 2题3－1图(a) 速度图(b) 加速度图解：pb ＝V B /μV ＝450/10＝45 mmμV =10 (mm/s)/mm μa ＝100 (mm/s 2)/mm题3－3图(a) (b)题3－2图图上尺寸 a ＝7.26 mmb ＝26.47 mmc 31＝18.58 mmd ＝28.02 mmc 32＝18.58 mmpa ＝22.8 mm V B ＝V A ＋V BApb ＝19.66 mmV B ＝19.66×50＝983 mm/s V 5＝ω3 c 32＝1.058×18.58×50＝983 mm/s速度图V A ＝a ω1=7.26×50×3.14＝1140.4 mm/s μV =50 (mm/s)/mmab dpω3＝V B /c 31＝983/(18.58×50)＝1.058 rad/s3－2 题3－2图所示为油田抽油机机构，D 1D 2为中心在O 3点、半径为c 32的圆弧，5为钢丝绳与抽油活塞组合体，长度比例尺μL ＝实际尺寸/图上尺寸＝50，ω1＝3.14 rad/s ，试用图解法求活塞5在图示位置的速度V 5（参考答案：V 5＝0.983 m/s ）。

机械原理第3版课件第三章

v
生无限值惯性力，并由此对凸轮产
生冲击

a
+∞
—— 刚性冲击

－∞
s = c0 c1 v = ds dt = c1 回程运动方程： a = dv dt = 0
边界条件
运动始点：=0, s=h 运动终点： = ，s=0
s = h (1 ) h v = ω a = 0 Nhomakorabeaf

从动件在运动起始、中点和终止点存在柔性冲击适用于中速轻载场合
f
O
f/2
4h2/f2

c)五次多项式运动规律表达式为
v = ds / dt = C1 2C2 3C3 2 4C4 3 5C5 4 a = dv / dt = 2C2 2 6C3 2 12C4 2 2 20C5 2 3 s = C0 C1 C2 2 C3 3 C4 4 C5 5
推程边界条件
在始点处：=0, s1=0, v1=0, a1=0；在终点处： = Φ s2=h, v2=0, a2=0；解得待定系数为
C0=0,C1=0,C2=0,C3=10h/Φ 3,C4=-15/ Φ4,C5=6h/ Φ5
位移方程式为
S=10hφ 3/ Φ3-15hφ4/Φ4+6hφ5/Φ5
第二节
凸轮机构基本运动参数设计
一、凸轮工作转角的确定
二、从动件运动规律设计
一、凸轮工作转角的确定
s
*从动件在远停处对应的转角s——远停角。
h
0
0
120º
s
180º
300º
360º

120º

机械原理第八版第三章

4
P23 P12 2
1 P16
P34 4 3
P36
P45 5
P56 6
§ 3 - 2 用图解法作机构的运动分析
【例3-5】用瞬心法对连杆—凸轮机构作速度分析
§ 3 - 3 用解析法作机构的运动分析
一、矢量方程解析法 1. 矢量分析的有关知识 2. 矢量方程解析法二、复数法三、矩阵法【例3-6】牛头刨床六杆机构
二、机构速度分析的便捷图解法多数机械的运动分析仅需对其机构作速度分析, 此时对于结构简单的机构采用速度瞬心图解法（简称速度瞬心法或瞬心法）对其进行速度分析就十分简便和直观。此外对于某些结构复杂的机构, 若单纯运用矢量方程图解法对其进行速度分析有时会遇到困难, 这时综合地运用这两种方法进行求解则往往显得比较简便
§ 3 - 2 用图解法作机构的运动分析
⑶ 矢量图的画法
大小：？大大Βιβλιοθήκη 大小：小小？：：
？？
大小：？
大小
大小
B
大小：？
A ：：？ D？
C
大小：？
大小：？
A
大大小
小：？
：
？
大小
B大：？小
：
？D
C
§ 3 - 2 用图解法作机构的运动分析
2.利用同一构件上两点间的速度和加速度矢量方程作图求解运动合成原理: 同一构件上任意一点的运动可认为是随该构件上基点作平动与绕基点作相对转动的合成 ⑴ 列矢量方程并分析各矢量 ⑵ 选取适当比例尺按方程作速度多边形及加速度多边形图 ⑶ 根据作图求解 ⑷ 速度及加速度影像
§ 3 - 2 用图解法作机构的运动分析
3.利用两构件重合点间的速度及加速度矢量方程作图求解运动合成原理: 构件i在重合点的运动可认为是随同构件j在重合点的运动和构件i相对于构件j的相对运动的合成重合点选取原则: 选已知参数较多的点（一般为铰链点），为此有时应将构件扩大至所选取的重合点 ⑴ 列矢量方程并分析各矢量 ⑵ 选取适当比例尺按方程作速度多边形及加速度多边形图 ⑶ 根据作图求解 ⑷ 科氏加速度存在的确定

机械原理第三章

a B2 B3
a
k B2 B3
23 VB2 B3
A
B2 1 △φ1 3 △φ3
2
(B2、B3)
k 的方向：把 a B2 B3
V B2 B3 的指向按
C
B˝2 B´2
(B3)
ω3的方向转过90°。
例题如图所示的机构中，设已知lAB=38mm， lBC=20mm， lDE=50mm ；原动件1以等角速度ω1 ＝10 rad/s沿顺时针方向回转。试用图解法求此时构件3的角速度ω3、角加速度α3以及E点的速度及加速度。
P P24 12
P13
4
VP24 l P14 P24
P24
P23
P34
P14 如果两构件的瞬心位于 P12 两个速度为零的瞬心的 2 连线之外，则两构件的为机构中原动件2与从动件 4 转向相同，否则，转向 4的瞬时角速度之比,称为机构的传动比或传递函数。相反。
例已知图示曲柄摇块机构各构件的长度，试在图上标出机构的全部瞬心位置。若已知曲柄的角速度ω1，试用瞬心法求构件3的角速度ω3 。
注意的问题1：哥氏加速度中的“牵连角速度的转向” 应该按照顺时针和逆时针的方向来判断，而不要只看箭头的指向。 ω1
1
B2
2
p b3
A
3
ω3
C
b2
正确
错误
A
1
ω1 3 2 B
vB2 vB3 vB2 B3
⊥AB ⊥BC ∥BC
√
？
p b3
？
VB3 3 0 l BC
C
b2
a
k B2 B3
VP23 3 l P13 P23 VP34 3 l P13 P34 VP23 3 lP13 P23 lP13 P23 VP34 3 lP13 P34 lP13 P34

机械原理第3章凸轮机构讲述

(逆时针)旋转。
关键：反转法
关键：反转法
1. 移动从动件盘形凸轮
（2）滚子从动件
已知：rb， , e, 滚子半径rr，s - 曲线。
反转法

滚子中心将描绘-条与凸轮廓线法向等距的曲线--理论廓线。Rb指的是理论廓线的基圆。

作内包络线，得到凸轮的实际廓线；若同时作外包络线，形成槽凸轮廓线
s
2h
2 2
2
2.等加速等减速(抛物线)运动
等加速阶段
4 h v 2
2
s
2h

2
a
4 h
2

2
3.2.2 从动件常用运动规律 2.等加速等减速(抛物线)运动
特点：加速度曲线有突变，加速度的变化率 ( 即跃度 j) 在这些位置为无穷大——柔性冲击适应场合：中速轻载

动件重力或其它外力
型锁合─利用高副元素本身的几何形状
优点：锁合方式结构简单
缺点：加大了凸轮的尺寸和重量
3.1凸轮机构的组成与类型
型锁合凸轮
等宽凸轮机构凸轮廓线上任意两条平行切线间的距离都等于框架内侧的宽度
等径凸轮机构两滚子中心间的距离始终保持不变缺点：从动件运动规律
缺点：从动件的运动规律的选择
2、移动平底从动件盘形凸轮机构刀具轨迹
用砂轮端面加工凸轮时平底上C的轨迹就是刀具中心
xc (rb s) sin xc (rb s) cos
B
3.3.3解析法设计凸轮廓线

3、摆动从动件盘形凸轮机构

B点的坐标方程
x OD CD y AD ED
B

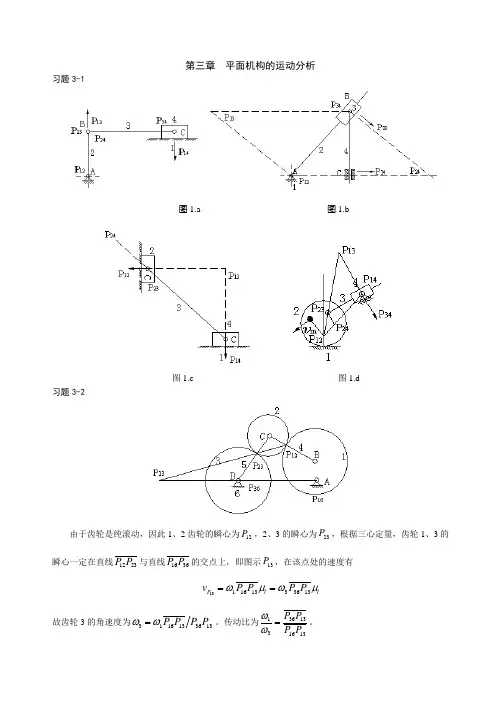
机械原理第三章习题答案

第三章平面机构的运动分析习题3-1图1.a 图1.b图1.c 图1.d习题3-2由于齿轮是纯滚动，因此1、2齿轮的瞬心为12P ，2、3的瞬心为23P ，根据三心定量，齿轮1、3的瞬心一定在直线2312P P 与直线3616P P 的交点上，即图示13P，在该点处的速度有 l l P P P P P v μωμω133631316113==故齿轮3的角速度为1336131613P P P ωω=。

传动比为1316133631P P P P =ωω。

习题3-3答：1)三个瞬心中，14P 、12P 为绝对瞬心，24P 为相对瞬心。

2)不利用其它的三个瞬心，因为它们全是相对瞬心。

3)构件2和4之间的转向关系可以根据瞬心24P 的瞬时绝对速度方向判断。

习题3-4 取比例尺为mmm l 003.0=μ，作图如下1) 由图上可知：l l P P P P P v μωμω241442412224==，根据量得的长度，得s rad P P P P /455.414.72/14.32102414241224=⨯==ωω 可计算出C 点的速度为：s m CD v l C /4.0003.030455.44=⨯⨯==μω2) 构件1、3的瞬心在点13P 处，且为绝对瞬心，因此构件3的角速度为 ()s rad C P v l c /53.2)67.52003.0/(4.0133=⨯==μω 显然构件3上速度最小点在E 点，则其速度为s m EP v l E /36.0003.04.4753.2133=⨯⨯==ω3) 要使0=C v ，需瞬心12P 、24P 重合(如图)，两位置分别为0126'=∠=DAB ϕ，02227''=∠=DAB ϕ。

第3章机械原理优秀课件

故相似，所以图形 bce 称之为图形BCE的速度影像。
（2）加速度求解步骤：
★ 求aC ①列矢量方程式
aC aB aCB aB aCnB aCt B
大小：？
√ 22lBC ?
方向：∥xx
⊥AB C→B ⊥AB 加速度多边形
②确定加速度比例尺 μa((m/s2)/mm) 极点 ③作图求解未知量：
◆通过运动副直接相联两构件的瞬心位置确定
转动副联接两构件的瞬心在转动副中心。
若为纯滚动, 接触点即为瞬心；
移动副联接两构件的瞬心在垂直于导路方向的无究远处。
若既有滚动又有滑动, 则瞬心在高副接触点处的公法线上。
三、机构中瞬心位置的确定（续） ◆ 不直接相联两构件的瞬心位置确定 P13
解：1. 画机构运动简图
A
2 B
ω2
D ω4 α4
ω3 a3 3 C
x
5E (E5,E6) 6 ω6 x
a6
2. 速度分析：
(1) 求vB:
（2）求vC: 大小
vB l AB 2
vCvBvCB
？√？
2 B
A
动件AB的运动规律和各构件尺寸。求：
①图示位置连杆BC的角速度
和其上各点速度。
②连杆BC的角加速度和其上 C点加速度。
解题分析：原动件AB的运动规律已知，则连杆BC上的B点速度和加速度是已知的，于是可以用
同一构件两点间的运动关系求解。
（1）速度解题步骤：
★求VC
①由运动合成原理列矢量方程式
不便；速度瞬心法只限于对速度进行分析, 不能分析机构的加速度；精度不高。
3-3 机构运动分析的矢量方程图解法
一、矢量方程图解法的基本原理和作法

机械原理第三章

（矢量方程及必要的分析计算）：
解：
方向⊥BD⊥AB∥BC
大小?1lAB?
利用速度影像原理求得c3点,
方向B→D⊥BD B→A⊥BC∥BC
大小??
利用加速度影像原理求得c3′点,
3—9在图示曲柄摇块机构中，已知lAB=30mm，lAC=100mm，lDE=40mm，lBD=50mm，φ1=45°，等角速度ω1=10rad/s，求点E的速度vE和加速度aE以及构件3的角速度3和角加速度3。
（矢量方程及必要的分析计算）：
解：１．速度分析
方向⊥CD⊥AB⊥CB
大小?1lAB?
vB=1lAB=5×0.15=0.75m/s
利用速度影像原理求得e点
方向水平⊥FE
大小??
2．加速度分析
方向C→D⊥CD B→A C→B⊥BC
大小32lCD?12lAB22lSC?+-
利用加速度影像原理求得e′点，
方向水平F→E⊥FE
第三章平面机构的运动分析
3—1试求下列各机构在图示位置时全部瞬心的位置(用符号Pij直接标注在图上)。
3—2在图示的四杆机构中，已知lAB=60mm，lCD=90mm，lAD=lBC=120mm，ω1=10rad/s，试用瞬心法求：
（1）当φ=165°时，点C的速度vC；
（2)当φ=165°时，构件2的BC线(或其延长线)上速度最小的点E的位置及速度的大小；
3—7哥氏加速度的机构图上标出
的方向，并写出其大小的表达式。
存在
存在
不存在不存在
3—8在图示的机构中，已知各杆的尺寸，1=常数。试用图解法求机构在图示位置构件3上C点的速度和加速度。
（画出机构的速度、加速度多边形，标出全部影像点，并列出必要的矢量方程式及计算式。）

机械原理英文版3齿轮

formula deduction
●Check pressure angle for roller follower check the case of self-lock ●Size of cam and follower
Cam Design
pinion
GEAR
Driving gear Transmission ratio
Cam Design
GEAR
Time varying output function
Noncircuilar Gear--printing press
Cam Design
GEAR
No slip in transmission
Synchronous belt –timing belt in automobile
30
45
●Equal divide base circle ●Envelope of tangent line ●Direction
review
Key points in cam chapter
● SVAJ curve ● graphical method for cam diagram ●Calculate coordinate for 3 typical cam
out d in mv in d out
Torque ratio?
Driven gear Spur Gear (直齿轮） external set
Cam Design
out d in mv in d out
GEAR
Rack and pinion
mv
put d in in d out
translation Internal set Spur Gear

机械原理第三章

运动：AB2 AB1
转角： 2
时间： t2
从动件c
DC1 DC2
t1
DC2 DC1
t2
从动件c的平均角速度：
DC1 DC2 :
3
t1
DC2 DC1 :
3
t2
t1
1 1
180 1
t2
2 1
180 - 1
t1 t2
3 3
行程速比系数
急回运动特性可用K表示：
K v2
t1
1
180
连杆机构的设计方法大体可分为图解法、解析法和实验法三大类。本章结合几种设计命题对这三种方法都有所介绍，但限于学时和篇幅，所讲内容是最基本的、有限的。同学若想深入学习和研究，可参阅张世民编著的《平面连杆机构设计》（北京：高等教育出版社, 1983）和A.G.厄尔德曼，G.N.桑多尔著，庄细荣等译的《机构设计————分析与综合（第一卷）（第二卷）》（北京：高等教育出版社，1992，1993）两书。前者对平面连杆机构的运动设计作了较深入的介绍，读者可以用它来解决更多的设计问题，书中不仅介绍了平面连杆机构设计的一些基础理论，而且在每一基
础理论之后都附有具体的应用实例；后者是一本内容丰富、观点新颖的教科书，其在连杆机构运动设计方面的内容之丰富是其它教科书无法相比的，书中既有较详细的设计方法介绍和理论分析，又有结合现代工业和生活实际的实例说明。
2. 根据给定的运动轨迹设计平面连杆机构，是工程实际中常见的设计命题之一。如本章所述，连杆曲线方程一般是一个六次方程，求解这样的方程，需要联立求解高阶非线性方程组。要求实现的精确点数目越多，求解越困难，而且还可能没有实数解，或即使有解，也可能由于结构尺寸不合理或传动角太小等原因而无实用价值。因此，在工程实际中, 人们常借助连杆曲线图谱来进行轨迹生成机构的设汁。J.A.Hrones和G.L.Helson所著的《Analysis of the Four-Bar Linkage》（New York：M.I.T-Wiley,1951)书，是这方面的一本经典著作，书中收集了7000 余张曲柄摇杆机构的连杆曲线图谱，包含了各种各样的轨迹曲线，利用它可以使设计过程大大简化。

机械原理第三章资料

红色三角形成立
d-a bc b d-a c
c d-a b
比较
adbc d-abc badc bd-ac cadb cd-ab
d-aadbc adbc bd-acadc bd-ac cd-abadb cd-ab
adbc
bd-ac
cd-ab
ac ab ad
a最短
a
b
c
d
该机构中构件a最短，构件a能否整周回转？
改变构件相对尺寸
双滑块机构
正弦机构
平面四杆机构的演化方式
(1) 改变运动副类型转动副移动副
(2) 改变相对杆长
(3) 选不同构件作机架
3-3 平面四杆机构有曲柄的条件及几个基本概念
一、平面四杆机构有曲柄的条件
1、铰链四杆机构有曲柄的条件
蓝色三角形成立
adbc
b cb c aa
d
ad
badc cadb
C
C
C
b B
aA
d
D
B
曲柄滑块机构的极位夹角
B
A
B
C
摆动导杆机构的极位夹角
B
A
Bd
e C
D
2. 急回运动
当曲柄等速回转的情况下，通
常把从动件往复运动速度快慢不同
C1
的运动称为急回运动。
b
c
主动件a
运动：AB1 AB2
时间： t1
转角：1
从动件c
DC1 DC2
t1
1 B2 b
a
a
A
2
d
B1
adbc bd-ac cd-ab
adbc abdc
acdb
ac ab ad

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

n
(4) Higher pair (rolling & sliding pair) Attention: Instant centre is not located at the point of contact or infinity！
V A1A2 1 n
2 A
P12 n
3.2.4 Theorem(定理) of Three Centres (Aronhold-Kennedy Theorem)
V A1A2 1 n
2 n A
(4) Higher pair (rolling & sliding pair) The direction of relative velocities, VA1A2 and VA2A1, between A1 and A2 must be along the common tangent(切线). Otherwise, the two links will separate(分离) or interfere(干涉). So the instant centre P12 or P21 must lie V A1A2 somewhere on the 2 P12 common normal n-n through the point A of n 1 contact. A
Let us consider any point, e.g. point C, outside the line P12P13.
C 2 A(P12 ) 1
3 B ( P13 )
V C 2C1 AC.
VC2C1 C 2 A(P12 ) 1 B ( P13 ) 3
V C 2C1 AC.
Since V C 2 V C1 V C 2C1 ,
V C 3C1 BC.
3.1.2 Methods：（1）Graphical method(图解法) (a) Geometrical(几何学的) method for position (b) Instant(瞬时的) centre method for velocity (c) Vector(矢量) equation method* （2）Analytical(解析的) method (a) Closed-loop method* (b) Assur group method （3）Experimental(实验) method*
1
(4) Higher pair (rolling & sliding pair)
2 1 A
(4) Higher pair (rolling & sliding pair) The direction of relative velocities, VA1A2 and VA2A1, between A1 and A2 must be along the common tangent(切线). Otherwise, the two links will separate(分离) or interfere(干涉).
Since P12 is the instantaneous(瞬时的) centre of relative rotation, VA2A1AP.
A 2 1
V A2A1
P12
Suppose that the positions of points A and B, the directions of VA2A1 and VB2B1 are known. The position of instant centre P12 V A2A1 is to be located. A
3.2.3 Location of the Instant Centre of Two Links Connected by a Kinematic Pair (1) Revolute pair If two links 1 and 2 are connected by a revolute pair, the centre of the revolute pair is obviously(明显地) the instant centre P12 or P21.
3 2 1
3.2.4 Theorem(定理) of Three Centres (Aronhold-Kennedy Theorem) Suppose that A is the instant centre P12 of the links 1 and 2. B is the instant centre P13 of the links 1 and 3. Where is P23? Any three links have three instant centres: P12, P13, and P23. They must 3 lie on a straight 2 A(P12 ) B ( P13 ) line. 1
V C 3C1 BC.
V C 2 C 1 V C 2 V C1 . Similarly, V C 3C1 V C 3 V C1. Obviously, for any point C outside the line P12P13, V C 2C1 V C 3C1 . Therefore, V C 2 V C 3 .
B 2 1 V B2B1
VA2A1AP. VB2B1BP.
A 2 1
V A2A1 B V B2B1 P12
3.2.2 Number N of instant centres: N=K(K-1)/2 Note: The frame is included in the number K. Classification(分类) of instant centres： (1) Absolute (绝对) instant centre: one of links is the frame. Its velocity is zero, but its acceleration may not be zero. (2) Relative(相对) instant centre: both links are moving links, velocity of which may not be zero.
2 A 1 P12 1 P12 2
(3) Sliding pair Relative translation(平移) is equivalent (等价于) to relative rotation about a point located at infinity(无穷远) in either direction perpendicular(垂直的) to the guideway(导路). Therefore, their instant centre lies at infinity in either direction perpendicular to the guideway. P12 Attention：The common normal(公法线) may pass 2 through any point !!
C B A
2 3
D E
ω1 θ 1
5
F
4
6
3.2 Velocity Analysis by the Method of Instant Centres(瞬心) 3.2.1 Definition of the Instant Centre(瞬心) 1. a pair of coincident(重合) points, the absolute(绝对) velocities of which are the same, in both magnitude(大小) and direction. 2. relative velocity is zero. V P2 V P1 3. Instantaneous(瞬时的) 2 centre of relative rotation, or more briefly the instant P12 1 centre, denoted(标为) as P12 or P21.
C B A
2 3
D E
ω1 θ 1
5
F
4
6
(4) Locate point E according to LDE and CDE.
C B A
2 3
D E
ω1 θ 1
5
F
4
6
(5)Draw an arc with the point E as the centre and LEF as the radius(半径). The intersection of the arc and the horizontal pathway(导路) is point F.
V C 3C1 BC.
V C 2 C 1 V C 2 V C1 . Similarly, V C 3C1 V C 3 V C1.
VC2C1 V C3C1 C 2 A(P12 ) 1 B ( P13 ) 3
V C 2C1 AC.
Since V C 2 V C1 V C 2C1 ,
C B A
2 3
D E
ω1 θ 1
5
F
4
6
(2)Locate B cording to LAB and 1
C B A
2 3
D E
ω1 θ 1
5
F
4
6
(3)Draw two arcs with the points B and D as the centres and LBC and LDC as the radii(半径复数). The intersection(交点) of the two arcs is point C.
All kinematics dimensions(LAD、LAB、 LBC、LDC、LDE、CDE、LEF) are known. Draw the kinematic diagram of the mechanism when 1=80.

机械原理(双语)第三章lecture3-1&2

合集下载

机械原理课后答案第3章

西北工大版机械原理第3章平面机构的运动分析精品PPT课件

机械原理第3章3[1].3

机械原理课件B第三章

南航机械原理课件第3章-3

机械原理双语

机械原理第3版课件第三章

机械原理第八版第三章

机械原理第三章

机械原理第3章凸轮机构讲述

机械原理第三章习题答案

第3章机械原理优秀课件

机械原理第三章

机械原理英文版3齿轮

机械原理第三章

机械原理第三章资料

文档推荐

最新文档