当前位置：文档之家 › 第九章统计热力学初步学习指导

第九章统计热力学初步学习指导

  • 格式：doc
  • 大小：554.50 KB
  • 文档页数：19

下载文档原格式

  / 19

合集下载

梁前德《统计学》(第二版)学习指导与习题训练答案：09第九章 统计综合评价 习题答案

梁前德《统计学》(第二版)学习指导与习题训练答案：09第九章 统计综合评价 习题答案

第九章统计综合评价习题答案一、名词解释用规范性的语言解释统计学中的名词。

1．统计综合评价：是根据分析研究的目的，依据已有的资料，运用统计方法，综合事物所处的具体环境，对现象总体的规模大小、水平高低、速度快慢、质量优劣等方面做出量的判断。

2. 功效系数法：是对多目标规划原理中的功效系数加以改进，经计算得到综合判断的分数。

3．德尔菲法：是借助专家的经验与主观判断的结果来确定各指标的权数，并在不断的反馈和修改中逐步得到比较满意的结果。

4. 指标比较法：是将相邻两个指标进行比较，以其中一个指标作为对比的基础，确定另一个指标的重要程度，并将重要程度数量化，依次顺序比较，确定各指标权数的方法。

5．变异系数法：是直接利用各指标所包含的信息计算出相应指标的权重，是一种客观赋权的方法。

二、填空题根据下面提示的内容，将准确的名词、词组或短语填入相应的空格之中。

11．统计指标、统计指标体系2．性质相同3．同度量4. 权数5. 定量方法、分析法6．标准值、标准值7．消除量纲、阈值、不容许值、满意值8．正态分布、0、19．直接、所包含的信息10．分值、分值三、选择题从各题给出的四个备选答案中，选择一个或多个正确答案，填入相应的括号中。

1．BCD 2. A 3. CD 4. AB 5. AD6. A7. AD8. AB9. BD 10. ABCD2四、判断改错对下列命题进行判断，在正确命题的括号内打“√”；在错误命题的括号内打“×”，并在错误的地方下划一横线，将改正后的内容写入题下空白处。

1. 变异系数法赋权是一种人工赋权法。

（×）客观2. 资产负债率、万元产值消耗能源比率和物耗率皆为逆指标。

（√）3. 进行归一化处理后，权数之和一定为1。

（√）4. 综合评价指标体系中的各指标要从同一方向说明总体。

（×）不一定5. 在对指标的无量纲处理时，如果指标是相对数，就不要进行无量纲处理。

（×）也要6. 在对学生的各科考试成绩进行综合评价时，各科考试成绩的单位都是分，因此就不需要进行无量纲化操作。

第九章-统计热力学初步-1

第九章-统计热力学初步-1

对非简并能级，只有一种粒子态。 对简并能级，则同一能级上可以有2个及2个以上的 粒子态。 若系统为独立子系统，则能级分布与状态分布都 同时满足
粒子数守恒 : N ni 能量守恒 : U ni i
(9-1)
18
9.2.2 分布的微观状态数WD与系统的总微观状态数Ω 例9.2.1 假定某种分子许可的非简并能级εi为0，ω，2ω，
解：
22
分布1：
WD,1＝4×(23) ＝4×8 ＝32
分布2：
WD,2＝6×(22) ×(32) ＝6×36 ＝ 216
系统的总微观状态数Ω
＝ 32＋216 ＝ 248
对于定域子系统分布的微观状态数WD
WD N!
i
gi
ni
ni !
23
对气体说来（即对离域子）：
WD
i
g i
离域子系统（又称全同粒子系统）。
定域子系统中的粒子彼 此可以分辨。例如，在晶体 中，粒子在固定的晶格位置 上作振动，每个位置可以想 象给予编号而加以区分，所 以定域子系统的微观态数是 很大的。
7
离域子系统：
离域子系统，基本粒 子之间不可区分。例如， 气体的分子，总是处于混 乱运动之中，彼此无法分 辨，所以气体是离域子系 统，它的微观状态数在粒 子数相同的情况下要比定 域子系统少得多。
WD ln ln WD ln WD * WD *
30
将lnWD在lnWD*附近按Taylor级数展开：
ln WD 1 2 ln WD (ni ) 2 ... ni ln WD ln WD * n 2 i ni 2 n * i i ni * i

09kj 统计热力学初步.

09kj 统计热力学初步.
数是离域子系统微态数的 N! 倍。
5．系统的总微态数
作为普遍规律，在 N，U，V 确定的情况下，系统的总
微态数是各种可能的能级分布方式具有的微态数的总和：
W = å WD
D
W 为N，U，V 的函数，即：
W = W(N ,U ,V )
2019/8/21
1．概率
§9.3 最概然分布与平衡分布
PA
=
lim
(PA ´ PB )
2. 等概率原理
N, U, V 确定的系统的微态均为属于能级 U 的简并态。
因此，假定每个微态出现的概率是相等的，即每个微态出 现的概率为
P
=
1
W (N ,U ,VLeabharlann )此即为等概率原理。
2019/8/21
3. 最概然分布
能级分布 D 的微态数为WD，因此分布 D 出现的概率为
PD
gv, v = 1
2019/8/21
3. 电子及核子运动 电子运动及核子运动的能级差一般都很大，因而分子中
的这两种运动通常均处于基态。也有例外的情况，如 NO 分子中的电子能级间隔较小，常温下部分分子将处于激发 态。本章为统计热力学初步，故对这两种运动形式只讨论 最简单的情况，即认为系统中全部粒子的电子与核子运动 均处于基态。
( ) ìïïïïï????????î
独立子系统 骣琪琪桫粒粒子子间间无相相互互作作用用可，忽或略
相依子系统
粒子间相互作用不能忽略
2019/8/21
气体、液体：离域子系统；固体：定域子系统。
本章只考虑独立子系统，包括独立离域子 系统及独立定域子系统。
N,U,V 确定的独立子系统
å Hˆ = N Hˆ i ，Hˆ i y i (rvi ) = ei y i (rvi ) i=1

大学物理第九章热力学讲解

大学物理第九章热力学讲解
过程中, 温度每升高(或降低) 10C,吸收的热量.
i C R
V2
单 i 3 双 i 5 多 i 6
i 气体分子的自由度
ν摩尔理想气体在等体过程中, 温度从T1升高到 T2(或降低) ,吸收的热量为
Q V
E - E
2
1
i RT - T
2
2
1

CV T2 - T1
2
1
2
2
1
V
Q E - E + pV V
p
2
1
2
1
C DT + RDT V
定压摩尔热容: 1mol 理想气体在等压过程中吸
收的热量dQp ，温度升高 dT，其定压摩尔热容为
dQ C p
dT p ,m
dQ C dT
p
p ,m
定压摩尔热容另一表述: 1mol 理想气体在等压
p
等 p2 体
升 压
p1
o
2 ( p2,V ,T2 )
1 ( p1,V ,T1)
V
V
T1 T2 Q 0 DE 0
QV
E1
E2
p
等 p1
体
降 压
p2
o
Q E - E i RT - T
V
2
1
2
2
1
1( p1,V ,T1)
2( p2,V ,T2 )
V
V
T1 T2 Q 0 DE 0
2 公式适用条件 气体压强不太大，温度不太低，密度不太高
例1 一容器内贮有氧气 0.10kg，压强为10atm， 温度为 470C。因容器漏气，过一段时间后，压强 减到原来的 5/8，温度降到 270C。问： （1）容器体积为多大？ （2）漏去了多少氧气？

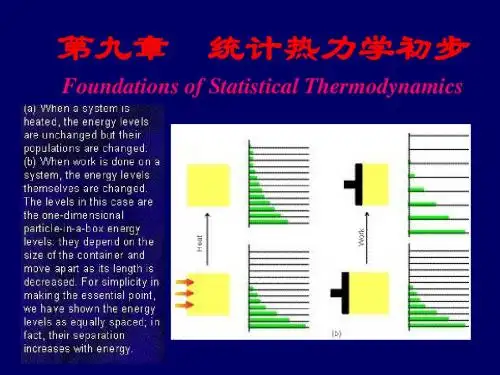
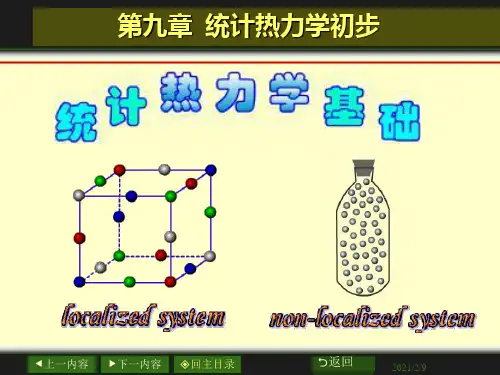
第9章统计热力学初步

第9章统计热力学初步

上一内容 下一内容 回主目录
返回
2021/2/9
9.1 粒子各运动形式的能级及能级的简并度
（5）简并度（统计权重，Degeneration）：某一能级所 对应的所有不同的量子状态 (简称量子态) 的数目。以符 号 g 表示。
能级，量子状态及简并度的关系：
一个能级相当于一个楼层，简并度相当于该楼层的房间 数目，一个粒子只要处于同一楼层，无论哪个房间，能量都 相等，但由于处于不同房间，因此处于不同的量子状态.
f转振3n3
例：单原子分子 双原子分子
n1 fr 0 fv 0 n2 fr 2 fv 1
线型多原子分子 nnfr 2 fv 3n5 非线型多原子分子 nn fr 3 fv 3n6
C2(O 3,2,4)、 N3(H 3,3,6) CH4(3,3,9)
上一内容 下一内容 回主目录
返回
2021/2/9
2
定域子系统
gv 1
根据
εv
υ 1hν 2
可能的能级：
v,0
1 2
h
v,1
3 2
h
v,2
5 2
h
v,3
7 2
h
上一内容 下一内容 回主目录
返回
2021/2/9
9.2 能级分布的微态数及系统的总微态数
v,0
1 2
hv
v,1
3 2
hv
v,2
5 2
hv
v,3
7 2
hv
能级 能级分布数
分布 n0 n1 n2 n3
注意：三者的大小关系！
上一内容 下一内容 回主目录
返回
2021/2/9
9.2 能级分布的微态数及系统的总微态数

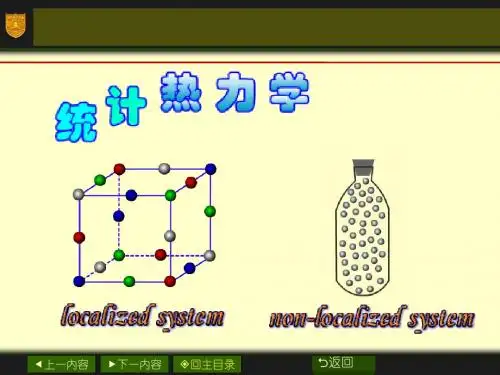
09章_统计热力学基础(2)

09章_统计热力学基础(2)

Ni i
t non −local
g =Π Ni!
由此可见，定位 体系与非定位体 系，最概然的分 布公式是相同的。
Ni i
∂ ln t + α + βε i = 0 ∂N i
−εi / kT * i
gi e N =N −εi / kT ∑gi e
i
上一内容 下一内容 回主目录
返回
上一内容 下一内容 回主目录
返回
根据
•根据对物质结构的某些基本假定 •实验所得的光谱数据 求得 •物质结构的一些基本常数 计算 •分子配分函数 计算 热力学性质
上一内容 下一内容 回主目录
返回
9.3 配分函数
配分函数的定义 配分函数的分离 非定位体系配分函数与热力学函数的关系 定位体系配分函数与热力学函数的关系
上一内容
下一内容
回主目录
返回
简并度（degeneration）
能量是量子化的，但每一个能级上可能有若 干个不同的量子状态存在，反映在光谱上就是代 表某一能级的谱线常常是由好几条非常接近的精 细谱线所构成。 量子力学中把能级可能有的微观状态数称为 该能级的简并度，用符号 gi 表示。
上一内容
下一内容
A,B,C
A B C BC AC AB BC AC AB A B C ABC 0 0 ABC
23=8 or
giN1,
上一内容
下一内容
回主目录
返回
有简并度时定位体系的微态数
先从N个分子中选出N1个粒子放在 1 1 能极 εε
N 上，有 C N 1 种取法；
但 ε1 能极上有 g1个不同状态，每个分子在ε1
求和的限制条件仍为：

第9章_统计热力学初步-wfz-1

第9章_统计热力学初步-wfz-1
13
§9.2 能级分布的微观状态数及系统的总微态数
1. 能级分布
平衡系统中, 粒子各能级的能量值只与粒子的性质及 V有关,所 以平衡系统中各能级的能量也完全确定
任何一种能级分布均应服从 粒子数及能量守恒关系：
ì U = ï ï ï í ï N = ni
å
i
由于粒子的不停运动并彼此交换 能量 , 使 N 、 U 、 V 确定的系统并非 只有一种能级分布。
h2 et = 8m
2 骣 2 2 ny nx nz 琪 琪 + + 琪 2 2 琪 a b c2 桫
(n x , n y , n z
势箱边长
= 1, 2, L
量子数
)
m 为分子质量 a、b、c 为容器边长 h 为Planck常数
yn
x ,n y ,n z
对应于量子数
n x , n y , n z的量子态
3
量子态: 系统中粒子所处的各种不同的微观状态. 能级: 粒子能量相同的一组量子态组成一个能级.不同能级的 能量 i值是不连续的, 即量子化的. 在一定宏观状态的独立子系统中, 系统的总粒子数N 和总能量U 是不变的, 若处于能级i的粒子数目为 ni ,必然有 N ni U ni i
11.622
10-
40
J
e t, 1 - e t, 0 = (11.622 - 5.811 )? 10-
40
J
5.811
10-
40
J
由以上计算知：平动子相邻能级的能量差Δ 非常小，所以平动子 很容易受激发而处于各能级。在常温下，平动子的量子化效应不突出， 可近似用经典力学方法处理。
10
2. 分子转动 双原子分子可近似看作原子间距 d 保持不变的刚性转子 . 转子的转动惯量 I :

物理化学 天津大学第四版 课后答案 第九章 统计热力学初步

物理化学 天津大学第四版 课后答案 第九章 统计热力学初步

0
0
2
4
6
8
10
12
c QuantumNumber J
差 ∆ε = 0.426 ×10−23 J ，试求 300
. K
时
I2
分子的 Θv
、 qv
、
q
0 v
及
f
0 v
。
hν ∆ε
w ∆ε
解：分子的振动特征温度为
=
hν , Θv
=
k
=
k
= 308.5 K
a 分子的振动配分函数为
d 1
1
q = e − e = e − e v
. nj+1 w nj
= exp(− ∆ε
kT
)
=
⎧5.409 ⎨
×
10 −7
for
⎩0.3553 for I 2
HCl
课 后 答 案 网
a 12．试证明离域子系统的平衡分布与定域子系统同样符合波尔兹曼分布，即
d ni =
N q
gi
exp {-
ei
kT }
h 略。
k 14．2 mol N2 置于一容器中，T = 400 K, p = 50 kPa ，试求容器中 N2 分子的平动 . 配分函数。
能级上粒子的分布数 n 与基态能级的分布数 n0 之比。
解：根据 Boltzma nn 分布
n n0
=
g g0
exp{− (ε
− ε0)
kT} =
g g0
exp{− 11× 0.1kT
kT}
g = 0.3329
g0
( ) 基态的统计权重 g0 = 1，能级
nx2

第九章 统计热力学

第九章 统计热力学

一、统计热力学在物理化学中的地位
大量微观粒子构成的宏观系统
宏观性质 →宏观性质
微观结构和运动 →宏观性质


宏观现象是微观运动的结果
宏观现象与微观现象有差别
研究 对象
以由大量微观粒子构成的宏观系统
研究方法
从物质的微观结构和微观运动形态出发，利用统计 平均的方法来获得物质的各种宏观性质
研究作用
统计热力学是联系物质宏观特性与微观性质的桥梁，它 弥补了热力学的不足，两者彼此联系，互相补充。 利用统计热力学方法不需要低温下的量热实验，就能求 得熵函数，其结果甚至比热力学第三定律所得的熵值更准确。
宏观系统是由大量微观粒子构成的。 对于总粒子数为N，总能量为U，体积为V的独 立子系统，每个粒子的能量是不完全相同的，并
且随着粒子之间的能量交换，每个粒子能量也是
变化的。但系统中总粒子数不变和系统总能量是 不变的，应遵循下面的关系式
一、独立子系统中粒子数和能量守衡关系式
N nj
状态分布
j
三、粒子各运动形式的能级及简并度
1. 三维平动子
能级公式：
讨论：
2 n 2 n 2 nz h x y t 2 2 8m a 2 b c 2
(9.1.1a)
1）式中:h 6.626 10
34
J s ,称为普郎克常数
2）式中(nx,ny,nz)是表示三维平动子每个量子状态的一组平动 量子数，分别说明三个互相垂直方向平动能的分量，其值只能
0 1
g0
2
g2
… … … · · ·
j
gj
· · ·
能级简并度 粒子分布数
g1
· · ·

物理化学第九章 统计热力学初步

物理化学第九章 统计热力学初步

统计热力学的基本任务
根据对物质结构的某些基本假定，以及实 验所得的光谱数据，求得物质结构的一些基本常 数，如核间距、键角、振动频率等，从而计算分 子配分函数。再根据配分函数求出物质的热力学 性质，这就是统计热力学的基本任务。
定域子系统和离域子系统
粒子（子）（particles) ——聚集在气体、液体、固 体中的分子、原子、离子等。
t r v e n
同时，其简并度等于各独立运动形式的简并度之 积：
g gt gr gv ge gn
运动自由度
对于一个具有n个原子的分子，通常有3n个自 由度，分别为： 3个平动自由度（xyz轴方向的平动） 3个转动自由度（围绕三个轴的旋转） 3n-6个振动自由度 对于线型分子，转动自由度为2（围绕线轴的 旋转可忽略），振动自由度为3n-5
系统的可能的能级分布方式有：
能级分布数
能级分布 n0
n1
n2 n3
Σni
Σniεi =9hν/2
Ⅰ 0 3 0 0 3 3×3 hν/2=9hν/2
Ⅱ 2 0 0 1 3 2×hν/2+1×7hν/2=9hν/2
Ⅲ 1 1 1 0 3 1×hν/2+1×3hν/2 +1×5hν/2=9hν/2
2.状态分布
1.分子的平动
t
h2 8m
(
nx2 a2
n2y b2
nz2 c2
)
对立方容器a=b=c，V=a3
t
h2 8mV 3 / 2
( nx2
n2y
nz2
)
量子力学中把能级可能有的微观状态数称为该 能级的简并度(degeneration)，用符号g表示。 简并度亦称为退化度或统计权重。

《天大考研资料 物理化学》第九章 统计热力学初步

《天大考研资料 物理化学》第九章 统计热力学初步
28
§9.4 玻尔兹曼分布
1. 玻尔兹曼分布 N个独立子(~1024)，处于平衡分布时，在 j 量子态上：
nj e j / kT
加上比例系数，有：
玻尔兹曼因子
nj e j / kT
当 i 能级上简并度为gi 时，有：
ni ginj giei / kT
29
按状态分布加和： N nj e j /kT
j
j
按能级分布加和： N
ni
g ei /kT i
i
i
N e j / kT
N g e i / kT
i
j
i
定义：q为粒子的配分函数：
q
e j / kT
g ei / kT i
j
i
nj
N q
e j / kT
ni
N q
giei / kT
Boltzmann分布
30
3. 玻尔兹曼分布的推导（拉格朗日代定系数法）
gvi
v2
2
(5/2)h 1
v1
1
(3/2)h 1
= h
v0
0
(1/2)h 1
10 kT
量子效应明显，不能按连续化处理 12
4. 电子与原子核
电子运动与核运动能级差一般都很大，
例：1
mol电子由基态
~ 400 kJ —-—-
第一能级
所以，粒子的这两种运动一般均处于基态。
其基态简并度：ge0 = 常数 gn0 = 常数
15
2. 状态分布:
当能级有简并或粒子可分辨的情况下，同一能级 上还可有多种状态分布
例：上题，如粒子可分辨（如图9.2.1）
分布I：n1 = 3，有 1 种状态分布； 分布II：n0 = 2， n3 = 1，有 3 种状态分布； 分布III：n0 = 1， n1 =1， n2 = 1，有 6 种状态分布

热力学与统计物理第九章系综理论

热力学与统计物理第九章系综理论
（2）正则系综： 由N、V、T不变的系统组成 （3）巨正则系综：由V、T、μ不变的系统组成
§微正则系综 （Microcanonical Ensemble）
一. 等概率假设
孤立系是与外界既无能量交换又无粒子交换的系统。 由于绝对的孤立系是没有的。所以精确的说，孤立 系是指能量在E～E+∆E之间，且∆E<<E的系统。尽 管∆E很小，但在此范围内，系统可能具有的微观状
(q, p) 是系统的某一微观态出现在Г空间中
(q, p) 处的概率。
说明：(1)推论：具有同一能量和同一粒子数的全 部微观状态都是可以经历的；因为只有它们 是可以经历的，才谈得上是等概率的
(2)微正则分布是平衡态统计系综理论中的唯一基 本假设，其正确性由它的推论与实际结果符合而 得到肯定 二.系统的微观态数
当粒子之间有很强的相互作用时，粒子除具有独 立的动能外。还有相互作用的势能，这样任何一个 微观粒子状态发生变化，都会影响其它粒子的运动 状态。这时某个粒子具有确定的能量和动量这句话 的意义已经含糊不清，因为它随时间变化。结果是 粒子不能从整个系统中分离出来。
处理粒子间有强相互作用这类问题，不能用粒 子相空间，而要用系统相空间，即把整个系统所对 应的每个可能的微观态集合起来进行考虑，直接从 整个系统的状态出发，不必过问个别粒子的状态。
令 : (N, E,V ) CV N
由: p ln N
kT V V
比较由实验得到的理想气体的物态方程：
pV nRT k R N0
即为玻尔兹曼常量。
四、应用 微正则分布求热力学函数的程序：
1.求出微观状态数Ω(N,E,V) 2.求熵S=ln Ω
3.从S(N,E,V) →E(S,N,V)
因此时刻t，系统的运动状态处于dΩ内的概率可

热力学统计物理-统计热力学课件第九章-49页PPT文档资料

热力学统计物理-统计热力学课件第九章-49页PPT文档资料

N,V
22
系统热平衡条件 ： 1 2
热力学中类似的两个系统达到热平衡的条件：
US11
N1,V1
US22
N2,V2
比较可得：
1 kT
Skln
S U
N ,V

1 T
——熵与微观状态数的关系—玻耳兹曼关系。
•不仅适用于近独立粒子系统，也适用于粒子间存在相
01.12.2019
1 E (E 11) 2(E 2) 1(E 1) 2 E (E 22) E E 1 20
ln E 11(E1)N1,V1 ln E 22 (E2)N2,V2 ——系统热平衡条件

lnE(E)



ln V
N
,E
lnN 11E1,V1 lnN 22E2,V2



ln N
E,V
1 1
1 2 1 2
01.12.2019
24
•参量的物理意义
全微分： d ln d E d V d N
开系的热力学基本方程：
dSdUpdVdN
TT T 比较可得：
01.12.2019
1 kT
p kT
kT
1 1
1 2 1 2
T1 T2 p1 p2
1 2
25
经典理想气体——确定常量k
(N,E,V)VN
在经典理想气体中，粒子的位置是互不相关的。一个 粒子出现在空间某一区域的概率与其它粒子的位置无关。 一个粒子处在体积为V的容器中，可能的微观状态数与V 成正比，N个粒子处在体积为V的容器中，可能的微观状 态数将与VN成正比。

第九章统计热力学初步学习指导

第九章统计热力学初步学习指导

第九章统计热力学初步8+2学时本章从最可几分布引出配分函数的概念，得出配分函数与热力学函数的关系。

由配分函数的分离与计算可求得简单分子的热力学函数与理想气体简单反应的平衡常数。

使学生了解系统的热力学宏观性质可以通过微观性质计算出来。

基本要求：1、理解统计热力学中涉及的一些基本概念如（定域子系统与非定位系统、独立粒子系统与相依粒子系统、微观状态、分布、最可几分布与平衡分布、配分函数）2、理解统计力学的三个基本假定。

理解麦克斯韦–玻尔兹曼分布公式的不同表示形式及其适用条件。

3、理解粒子配分函数的物理意义和析因子性质。

4、明确配分函数与热力学函数间的关系5、了解平动、转动、振动对热力学函数的贡献，了解公式的推导过程。

6、学会利用物质的吉布斯自由能函数、焓函数计算化学反应的平衡常数与热效应。

7、学会由配分函数直接求平衡常数的方法重点：1．平衡分布和玻耳兹曼分布公式；2．粒子配分函数的定义、物理意义及析因子性质；3．双原子分子的平动、转动和振动配分函数的计算；4．热力学能与配分函数的关系式；5．熵与配分函数的关系式；玻耳兹曼熵定理。

难点：1. 粒子配分函数的定义、物理意义及析因子性质；2. 双原子分子的平动、转动和振动配分函数的计算。

第九章统计热力学初步主要公式及其适用条件1. 分子能级为各种独立运动能级之和2. 粒子各运动形式的能级及能级的简并度（1）三维平动子简并度：当a = b = c时有简并,()相等的能级为简并的。

（2）刚性转子（双原子分子）：其中。

简并度为：g r,J = 2J +1。

（3）一维谐振子其中分子振动基频为，k为力常数，μ为分子折合质量。

简并度为1，即g v,ν = 1。

（4）电子及原子核全部粒子的电子运动及核运动均处于基态。

电子运动及核运动基态的简并度为常数。

3.能级分布微态数定域子系统：离域子系统：温度不太低时（即时）：一般情况下：系统总微态数：4. 等概率定理在N，V，U确定的情况下，系统各微态出现的概率相等。

热力学统计物理知识结构与学习方法指导

热力学统计物理知识结构与学习方法指导

热力学统计物理知识结构与学习方法指导
一、背景与基础知识
要求掌握高等数学知识。

特别是要求熟悉多元函数微积分、级数、概率论等。

掌握基础物理的全部内容，特别是热学、理论力学、量子物理基础等。

二、知识体系
三、学习方法指导
学习过程中，应特别注意对于热力学与统计物理研究问题的独特物理思想方法的思考和理解，以便学习到该门课程的精髓。

学习过程中，要注意运用整体性原理这一现代教学理论，掌握该课程的知识体系与研究方法。

弄清知识的间的联系、地位，发挥知识整体功能，注重知识的应用能力培养。

学习要经历两个过程一是把书读厚的过程，即深挖知识的内涵和外延；二是把书读薄，即整理出知识体系，弄清知识之间联系。

学习过程中，注重“构建主义”现代教学理论和方法的运用，重现物理学家研究问题的背景和发现过程，培养自己较强的独立思考能力和创新能力。

使学会运用科学的学习方法，真正达到从学会到会学。

在学有余力的情况下，针对课程中的问题，阅读有关课程研究文献，了解对于有关问题的较为深入的研究结论，扩展知识。

选择简单课题，作一些初步研究，培养自己的创新意识和初步研究能力。

对和前沿接轨部分的知识点，在学好的基础上，了解相关前沿发展。

另外有关注热力学统计物理理论在实际的重要应用，理解从理论到应用的方法，培养自己运用所学基础知识，解决实际问题的意识和能力。

打算考研的学生，在学好教材知识点的基础上，适当拓宽，加深学习内容是必要的。

另外，要注意收集有关院校的科研题目，了解他们对知识的考核侧重点。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第九章统计热力学初步8+2学时本章从最可几分布引出配分函数的概念，得出配分函数与热力学函数的关系。

由配分函数的分离与计算可求得简单分子的热力学函数与理想气体简单反应的平衡常数。

使学生了解系统的热力学宏观性质可以通过微观性质计算出来。

基本要求：1、理解统计热力学中涉及的一些基本概念如（定域子系统与非定位系统、独立粒子系统与相依粒子系统、微观状态、分布、最可几分布与平衡分布、配分函数）2、理解统计力学的三个基本假定。

理解麦克斯韦–玻尔兹曼分布公式的不同表示形式及其适用条件。

3、理解粒子配分函数的物理意义和析因子性质。

4、明确配分函数与热力学函数间的关系5、了解平动、转动、振动对热力学函数的贡献，了解公式的推导过程。

6、学会利用物质的吉布斯自由能函数、焓函数计算化学反应的平衡常数与热效应。

7、学会由配分函数直接求平衡常数的方法重点：1．平衡分布和玻耳兹曼分布公式；2．粒子配分函数的定义、物理意义及析因子性质；3．双原子分子的平动、转动和振动配分函数的计算；4．热力学能与配分函数的关系式；5．熵与配分函数的关系式；玻耳兹曼熵定理。

难点：1. 粒子配分函数的定义、物理意义及析因子性质；2. 双原子分子的平动、转动和振动配分函数的计算。

第九章统计热力学初步主要公式及其适用条件1. 分子能级为各种独立运动能级之和2. 粒子各运动形式的能级及能级的简并度（1）三维平动子简并度：当a = b = c时有简并,()相等的能级为简并的。

（2）刚性转子（双原子分子）：其中。

简并度为：g r,J = 2J +1。

（3）一维谐振子其中分子振动基频为，k为力常数，μ为分子折合质量。

简并度为1，即g v,ν = 1。

（4）电子及原子核全部粒子的电子运动及核运动均处于基态。

电子运动及核运动基态的简并度为常数。

3.能级分布微态数定域子系统：离域子系统：温度不太低时（即时）：一般情况下：系统总微态数：4. 等概率定理在N，V，U确定的情况下，系统各微态出现的概率相等。

5. 玻尔兹曼分布（即平衡分布，也即最概然分布）Stirling公式：粒子的配分函数：玻尔兹曼分布：能级i的有效容量：6. 配分函数的析因子性质7. 能量零点的选择对配分函数的影响若基态能级能量值为，以基态为能量零点时，能量值常温下，平动及转动配分函数与能量零点选择几乎无关，但振动配分函数与能量零点选择有关。

即：电子运动与核运动的配分函数，与能量零点选择也有关。

8.配分函数的计算平动:转动（对线性刚性转子）：其中若设，则当T >> Q r时，，其中σ为绕通过质心，垂直于分子的轴旋转一周出现的不可分辨的几何位置的次数，即分子对称数。

对线性刚性转子转动自由度为2。

振动:若设，当T<<Q v时（常温）,振动运动量子化效应突出，不能用积分代替加和：电子运动: 因为电子运动全部处于基态，电子运动能级完全没有开放，求和项中自第二项起均可被忽略。

所以：核运动:9. 热力学能与配分函数的关系此处U i可代表：（1）总热力学能；（2）零点为e0时的热力学能（U0 = U - Nε0）；（3）平动能；q i表示相应的配分函数。

（4）当U i代表：转动能，振动能，电子能，核能时，q i与V无关，偏微商可写作全微商。

U i与U i0关系：只有，其余：。

10. 摩尔定容热容与配分函数关系，ε0与T无关。

所以，C v,m与零点能选择无关。

11. 玻尔兹曼熵定理摘取最大项原理：若最概然分布微态数为W B，总微态数为Ω，当N无限增大时，，所以可用ln W B代替lnΩ。

这种近似方法称为摘取最大项原理。

12. 熵与配分函数关系离域子系统：（熵与零点能的选择无关）定域子系统：由于，配分函数的析因子性质，及对离域子系统，各独立运动的熵可表示为：13. 统计熵的计算一般物理化学过程，只涉及S t ,S r ,S v(N0为阿佛加得罗常数)14. 其它热力学函数与配分函数的关系离域子：,定域子：,其它G ，H 可由热力学关系导出。

15. 理想气体的标准摩尔吉布斯函数16. 理想气体的标准摩尔吉布斯自由能函数17. 理想气体的标准摩尔焓函数第九章 统计热力学初步 概念题一.思考题1.斯特林公式：NeN N )(!≈ 的适用条件是什么？用此式计算N = 10，N = 50时，误差各为多少？2.在低温条件下，能否用公式：rr Tq Θ=σ计算转动配分函数？为什么？ 3.四种分子的有关参数如下：在同温同压下，那种气体的m t S ,最大？那种气体的m r S ,最大？ 那种分子的震动频率最小。

4.由热力学能公式VT q NkT U ⎥⎦⎤⎢⎣⎡∂∂=ln 2可知，只要求得分子配分函数q ，就可以计算出系统的热力学能。

这与热力学中所说“热力学能绝对值不可知”矛盾吗？ 5.在状态函数U ，S ，H ，A 和G 中，那些对定域子系统和离域子系统是相同的？ 6.零点能的不同选择，对状态函数U ，S ，H ，A ，G ，C V 中那些没有影响？ 7.对单原子理想气体在室温下的一般物理化学过程，若用配分函数q 来求热力学函数的变化，在 n e v r t q q q q q ,,,, 各配分函数中，最小须得到那几种即可？为什么？二.选择题1. 统计热力学主要研究（ ）。

A. 平衡系统B. 近平衡系统C. 非平衡系统 E. 单个粒子的行为 2. 系统的微观性质和宏观性质是通过（ ）联系起来的。

A.热力学B.化学动力学C.统计力学D. 量子力学 3. 统计热力学研究的主要对象是（ ）A. 微观粒子的各种变化规律B. 宏观体系的各种性质C. 微观粒子的运动规律D.宏观系统的平衡性质E. 体系的宏观性质与微观结构的关系4.下述诸系统中，属独粒子系统的是（ ）A.纯液体B.理想液态溶液C.理想的原子晶体D.理想气体E.真实气体 5. 对于一个U ，N ，V 确定的系统，其微观状态数最大的分布就是最概然分布，得出这一结论的理论依据是：（ ）A.玻兹曼分布定律B.等几率假设C.分子运动论D. 统计学原理E.能量均分原理6.各种不同运动状态的能级间隔是不同的，对于同一种气体分子，其平动、转动、振动和电子运动的能级间隔的大小顺序是：（）A. ∆εt > ∆εr > ∆εv > ∆εeB. ∆εt < ∆εr < ∆εv < ∆εeC. ∆εe > ∆εv > ∆εt > ∆εrD. ∆εv > ∆εe > ∆εt > ∆εrE. ∆εr > ∆εt > ∆εe > ∆εv7. 在统计热力学中，对物系的分类按其组成的粒子能否被分辨来进行，按此原则：（）A. 气体和晶体皆属定域子系统B. 气体属离域子系统而晶体属定域子系统C. 气体和晶体皆属离域子系统D. 气体属定域子系统而晶体属离域子系统8. 对于定域子系统分布X所拥有的微观状态t x为：（）A. B.C. D.9. 对给定的热力学系统,任何分布应满足：（）A. ∑Ni =N B. ∑Niεi=U C. N 及V 一定 D. ∑Ni=N 及∑Niεi=U10.粒子的配分函数q是表示 ( )A.一个粒子的玻兹曼因子；B. 对一个粒子的玻兹曼因子取和；C. 对一个粒子的所有可能状态的玻兹曼因子取和；D. 对一个粒子的简并度和玻兹曼因子的乘积取和．11.当系统的U，N，V确定后，则：（）A. 每个粒子的能级ε1, ε2, ....., εi一定，但简并度g1, g2, ....., g i及总微观状态数Ω不确定。

B. 每个粒子的能级ε1, ε2, ....., εi不一定，但简并度g1, g2, ....., g i及总微观状态数Ω皆确定。

C. 每个粒子的能级ε1, ε2, ....., εi和简并度g1,g2, ....., g i皆可确定，但微观状态数Ω不确定。

D. 每个粒子的能级ε1, ε2, ....., εi和简并度g1, g2, ....., g i及微观状态数Ω 均确定。

12.玻兹曼统计认为 ( )A. 玻兹曼分布就是最可几分布, 也就是平衡分布；B. 玻兹曼分布不是最可几分布, 也不是平衡分布；C. 玻兹曼分布只是最可几分布, 但不是平衡分布；D. 玻兹曼分布不是最可几分布, 但却是平衡分布．13.经典粒子的零点能标度选择不同时, 必定影响 ( )A. 配分函数的值；B. 粒子的分布规律；C.体系的微观状态数；D. 各个能级上粒子的分布数；E. 各个量子态上粒子的分布数．14.对定域子系统和离域子系统, 其热力学函数的统计表达式形式相同的是 ( )A. S、F、G；B. H、F、G；C. U、H、C V；D. U、F、C V；E. U、S、C V．15.分子能量零点的不同选择所产生的影响中, 下述哪一点是不成立的？( )A. 能量零点选择不同, 各能级的能量值也不同；B. 能量零点选择不同, 其玻兹曼因子也不同；C. 能量零点选择不同, 分子的配分函数也不同；D. 能量零点选择不同, 玻兹曼分布公式也不同．16.对一个N,U,V确定的系统, 沟通宏观和微观、热力学与统计力学的桥梁是 ( )A.F = -kT ln q；B. S = k lnΩ；C. 配分函数q；D. p = NkT(∂ln q/∂V)T,NE. ∑=iii NUε17.关于粒子配分函数的量纲, 正确的说法是 ( )A. 所有配分函数都无量纲；B. 定域子和离域子的配分函数的量纲不同。

C. 所有配分函数的量纲都是J·mol-1；C. 所有配分函数的量纲都是J·K；18.对于玻兹曼分布, 下面的表述中不正确的是 ( )A. 玻兹曼分布就是平衡分布；B. 玻兹曼分布就是微观状态数最大的分布；C. 最可几分布一定是玻兹曼分布；D. 有些理想气体不服从玻兹曼分布。

19.对于单原子理想气体在室温下的一般物理化学过程, 若欲通过配分函数来求过程中热力学函数的变化 ( )A. 必须同时获得q t、q r、q v、q e、q n各配分函数的值才行；B. 只须获得q t这一配分函数的值就行；C. 必须获得q t、q r、q v诸配分函数的值才行；D. 必须获得q t、q e、q n诸配分函数的值才行。

20.通过对谐振子配分函数的讨论, 可以得出 1mol 晶体的热容C V,m=3R, 这一关系与下列哪一著名定律的结论相同？ ( )A. 爱因斯坦(Einstein)定律；B. 杜隆-柏蒂(Dulong-Petit)定律；C. 德拜(Debye)立方定律；D. 玻尔兹曼分布定律．21.根据热力学第三定律, 对于完美晶体, 在S0 = k lnΩ 0 中, 应当是 ( )A. Ω 0 = 0；B. Ω 0< 0；C. Ω 0 = 1；D. Ω 0> 1；E. Ω0< 1．22.在298K、体积为10-3dm3的容器内, Cl2分子(M=35.45)的平动配分函数是 ( )A. 5.796×1029；B. 5.796×1026J·mol-1；C. 5.796×1029J·mol-1；D. 5.796×1026；E. 5.796×1029J·K．23.下列分子中对称数为3的是 ( )A. H2； B. HBr； C. NH3； D. 邻二溴苯(o-dibromobenzene)；E. 对二溴苯(p-dibromobenzene)．24.若已知H2的转动量子数J=1, 两原子的核间距r=0.74×10-10m, 氢原子质量mH=1.673×10-27kg, 普朗克常数h=6.626×10-34J·s, 则1mol H2的转动能为 ( )A. U r=7.43×10-54J；B. U r=3.67×10-54J；C. U r=4.86×10-21J；D. U r=1.215×10-21J；E. U r=2.43×10-21J．25.若一双原子分子的振动频率为 4×1013s, h=6.626×10-34J·s, k=1.38×10-23J·K-1, 则其振动特征温度为 ( )A. 83.3K；B. 1920.58K；C. 19.21K；D. 833K；E. 120.03K．三.判断题：1．当系统的U，V，N一定时，由于粒子可以处于不同的能级上，因而分布数不同，所以系统的总微态数Ω不能确定。