【苏教版】高中数学选修4-2《矩阵与变换》.2.4 旋转变换

专题一请同学从下面所给的三题中选定两题作答【题目1】 选修4－2：矩阵与变换设矩阵A ＝⎣⎡⎦⎤m 00 n ，若矩阵A 的属于特征值1的一个特征向量为⎣⎡⎦⎤10，属于特征值2的一个特征向量为⎣⎡⎦⎤01，求矩阵A .【题目2】 选修4－4：坐标系与参数方程已知直线l ：⎩⎨⎧x ＝1＋t ，y ＝－t (t 为参数)与圆C ：⎩⎨⎧x ＝2cos θ，y ＝m ＋2sin θ(θ为参数)相交于A ，B 两点，m 为常数. (1)当m ＝0时，求线段AB 的长；【题目1】 甲、乙两人投篮命中的概率分别为23与12，各自相互独立.现两人做投篮游戏，共比赛3局，每局每人各投一球.(1)求比赛结束后甲的进球数比乙的进球数多1个的概率；(2)设ξ表示比赛结束后甲、乙两人进球数的差的绝对值，求ξ的分布列和数学期望E (ξ).解 (1)比赛结束后甲的进球数比乙的进球数多1个有以下几种情况：甲进1球，乙进0球；甲进2球，乙进1球；甲进3球，乙进2球.所以比赛结束后甲的进球数比乙的进球数多1个的概率为【题目2】 在(1＋x ＋x 2)n ＝D 0n ＋D 1n x ＋D 2n x 2＋…＋D r n x r ＋…＋D 2n －1n x 2n －1＋D 2n n x 2n 的展开式中，把D 0n ，D 1n ，D 2n，…，D 2n n 叫做三项式系数. (1)当n ＝2时，写出三项式系数D 02，D 12，D 22，D 32，D 42的值；(2)类比二项式系数性质C m n ＋1＝C m －1n ＋C m n (1≤m ≤n ，m ∈N ，n ∈N )，给出一个关于三项式系数 .专题二请同学从下面所给的三题中选定两题作答【题目1】 选修4－2：矩阵与变换已知曲线C ：y 2＝12x ，在矩阵M ＝⎣⎡⎦⎤1 00 －2对应的变换作用下得到曲线C 1，C 1在矩阵N ＝⎣⎡⎦⎤0 11 0对应的变换作用下得到曲线C 2，求曲线C 2的方程.【题目2】 选修4－4：坐标系与参数方程在平面直角坐标系xOy 中，圆的参数方程为⎩⎨⎧x ＝2＋2cos α，y ＝2sin α(α为参数)，以坐标原点O 为极点，x 轴的正半轴为极轴建立极坐标系.求： (1)圆的普通方程；(2)圆的极坐标方程.必做部分【题目1】如图，在多面体ABCDEF中，ABCD为正方形，ED⊥平面ABCD，FB∥ED，且AD＝DE＝2BF＝2.(1)求证：AC⊥EF；(2)求二面角C－EF－D的大小.【题目2】已知k，m∈N*，若存在互不相等的正整数a1，a2，…，a m，使得a1a2，a2a3，…，a m－1a m，a m a1同时小于k，则记f(k)为满足条件的m的最大值.(1)求f(6)的值；(2)对于给定的正整数n (n ＞1)，(ⅰ)当n (n ＋2)＜k ≤(n ＋1)(n ＋2)时，求f (k )的解析式；(ⅱ)当n (n ＋1)＜k ≤n (n ＋2)时，求f (k )的解析式.专题三请同学从下面所给的三题中选定两题作答【题目1】 选修4－2：矩阵与变换设二阶矩阵A ，B 满足A －1＝⎣⎡⎦⎤1 23 4，(BA )－1＝⎣⎡⎦⎤1 00 1，求B －1.【题目2】 选修4－4：坐标系与参数方程在极坐标系中，已知曲线C ：ρ＝2sin θ，过极点O 的直线l 与曲线C 交于A ，B 两点，且AB ＝3，求直线l 的方程.必做部分【题目1】某校高一、高二两个年级进行乒乓球对抗赛，每个年级选出3名学生组成代表队，比赛规则是：①按“单打、双打、单打”顺序进行三盘比赛；②代表队中每名队员至少参加一盘比赛，但不能参加两盘单打比赛.若每盘比赛中高一、高二获胜的概率分别为37，4 7.(1)按比赛规则，高一年级代表队可以派出多少种不同的出场阵容？(2)若单打获胜得2分，双打获胜得3分，求高一年级得分ξ的概率分布列和数学期望.【题目2】 已知抛物线C ：x 2＝2py (p ＞0)过点(2，1)，直线l 过点P (0，－1)与抛物线C 交于A ，B 两点.点A 关于y 轴的对称点为A ′，连接A ′B .(1)求抛物线C 的标准方程；(2)问直线A ′B 是否过定点？若是，求出定点坐标；若不是，请说明理由. 专题4请同学从下面给的三题中选定两题作答【题目1】 选修4－2：矩阵与变换已知矩阵A ＝⎣⎡⎦⎤1 2c d (c ，d 为实数).若矩阵A 属于特征值2，3的一个特征向量分别为⎣⎡⎦⎤21，⎣⎡⎦⎤11，求矩阵A 的逆矩阵A －1.【题目2】 选修4－4：坐标系与参数方程已知直线l 的极坐标方程为ρsin ()θ－π3＝3，曲线C 的参数方程为⎩⎨⎧x ＝2cos θ，y ＝2sin θ(θ为参数)，设点P 是曲线C 上的任意一点，求P 到直线l 的距离的最大值.必做部分【题目1】 如图，在直三棱柱ABC －A 1B 1C 1中，已知CA ＝CB ＝1，AA 1＝2，∠BCA ＝90°.(1)求异面直线BA 1与CB 1夹角的余弦值；(2)求二面角B－AB1－C平面角的余弦值.【题目2】在数列{a n}中，已知a1＝20，a2＝30，a n＋1＝3a n－a n－1(n∈N*，n≥2).(1)当n＝2，3时，分别求a2n－a n－1a n＋1的值，并判断a2n－a n－1a n＋1(n≥2)是否为定值，然后给出证明；(2)求出所有的正整数n，使得5a n＋1a n＋1为完全平方数.专题五2.(2018·江苏省盐城中学调研)已知矩阵M ＝⎣⎡⎦⎤0 ab 0满足：Ma i ＝λi a i ，其中λi (i ＝1,2)是互不相等的实常数，a i (i ＝1,2)是非零的平面列向量，λ1＝1，a 2＝⎣⎡⎦⎤11，求矩阵M .3.(2018·苏州、南通等六市模拟)在极坐标系中，求以点P ()2，π3为圆心且与直线l: ρsin ()θ－π3＝2相切的圆的极坐标方程.5.已知点A(1,2)在抛物线F：y2＝2px上.(1)若△ABC的三个顶点都在抛物线F上，记三边AB，BC，CA所在直线的斜率分别为k1，k2，k3, 求1k1－1k2＋1k3的值；(2)若四边形ABCD的四个顶点都在抛物线F上，记四边AB，BC，CD，DA所在直线的斜率分别为k1，k2，k3，k4，求1k1－1k2＋1k3－1k4的值.6.已知f n (x )＝C 0n x n －C 1n (x －1)n ＋…＋(－1)k C k n (x －k )n ＋…＋(－1)n C n n (x －n )n ，其中x ∈R ，n ∈N *，k ∈N ，k ≤n .(1)试求f 1(x )，f 2(x )，f 3(x )的值；(2)试猜测f n (x )关于n 的表达式，并证明你的结论. .专题六2.(2018·苏州、南通等六市模拟)在平面直角坐标系xOy 中，已知A ()0，0，B ()3，0，C ()2，2.设变换T 1, T 2对应的矩阵分别为M ＝⎣⎡⎦⎤1 02， N ＝⎣⎡⎦⎤2 00 1，求对△ABC 依次实施变换T 1, T 2后所得图形的面积.3.已知两个动点P ，Q 分别在两条直线l 1：y ＝x 和l 2：y ＝－x 上运动，且它们的横坐标分别为角θ的正弦，余弦，θ∈[0，π]，记OM →＝OP →＋OQ →，求动点M 的轨迹的普通方程.5.甲、乙两人轮流投篮，每人每次投一次篮，先投中者获胜，投篮进行到有人获胜或每人都已投球3次时结束.设甲每次投篮命中的概率为25，乙每次投篮命中的概率为23，且各次投篮互不影响.现由甲先投.(1)求甲获胜的概率；(2)求投篮结束时甲的投篮次数X的概率分布与数学期望.6.设n 个正数a 1，a 2，…，a n 满足a 1≤a 2≤…≤a n (n ∈N *且n ≥3). (1)当n ＝3时，证明：a 1a 2a 3＋a 2a 3a 1＋a 3a 1a 2≥a 1＋a 2＋a 3；(2)当n ＝4时，不等式a 1a 2a 3＋a 2a 3a 4＋a 3a 4a 1＋a 4a 1a 2≥a 1＋a 2＋a 3＋a 4也成立，请你将其推广到n (n ∈N *且n ≥3)个正数a 1，a 2，…，a n 的情形，归纳出一般性的结论并用数学归纳法证明.专题七2.若二阶矩阵M 满足⎣⎢⎡⎦⎥⎤－2122－1M ＝⎣⎡⎦⎤－3 0 4－1，求曲线4x 2＋4xy ＋y 2－12x ＋12y ＝0在矩阵M 所对应的变换作用下得到的曲线的方程.3.已知直线的极坐标方程为ρsin ()θ＋π4＝22，圆M 的参数方程为⎩⎨⎧x ＝2cos θ，y ＝－2＋2sin θ(其中θ为参数).(1)将直线的极坐标方程化为直角坐标方程； (2)求圆M 上的点到直线的距离的最小值.5.如图，在直三棱柱ABC －A 1B 1C 1中，AA 1＝AB ＝AC ＝2，AB ⊥AC ，M 是棱BC 的中点，点P 在线段A 1B 上.(1)若P 是线段A 1B 的中点，求直线MP 与直线AC 所成角的大小；(2)若N 是CC 1的中点，直线A 1B 与平面PMN 所成角的正弦值为77，求线段BP 的长度.6.已知()1＋12xn展开式的各项依次记为a 1(x )，a 2(x )，a 3(x )，…，a n(x )，an ＋1(x ).设F (x )＝a 1(x )＋2a 2(x )＋3a 3(x )＋…＋na n (x )＋(n ＋1)·a n ＋1(x ).(1)若a 1(x )，a 2(x )，a 3(x )的系数依次成等差数列，求n 的值； (2)求证：对任意x 1，x 2∈[0,2]，恒有|F (x 1)－F (x 2)|≤2n －1(n ＋2)－1专题一请同学从下面所给的三题中选定两题作答 【题目1】 选修4－2：矩阵与变换设矩阵A ＝⎣⎡⎦⎤m 0n ，若矩阵A 的属于特征值1的一个特征向量为⎣⎡⎦⎤10，属于特征值2的一个特征向量为⎣⎡⎦⎤01，求矩阵A .解 由题意得⎣⎡⎦⎤m 00 n ⎣⎡⎦⎤10＝1⎣⎡⎦⎤10，⎣⎡⎦⎤m 00 n ⎣⎡⎦⎤01＝2⎣⎡⎦⎤01，所以⎩⎨⎧m ＝1，n ＝2，故A ＝⎣⎡⎦⎤1 00 2. 【题目2】 选修4－4：坐标系与参数方程已知直线l ：⎩⎨⎧x ＝1＋t ，y ＝－t (t 为参数)与圆C ：⎩⎨⎧x ＝2cos θ，y ＝m ＋2sin θ(θ为参数)相交于A ，B 两点，m 为常数.(1)当m ＝0时，求线段AB 的长；(2)当圆C 上恰有三点到直线的距离为1时，求m 的值. 解 (1)直线l ：x ＋y －1＝0，曲线C ：x 2＋y 2＝4，圆心到直线的距离d ＝12，故AB ＝2r 2－d 2＝14. (2)圆C 的直角坐标方程为x 2＋(y －m )2＝4，直线l ：x ＋y －1＝0，由题意，知圆心到直线的距离d ＝|m －1|2＝1，∴m ＝1± 2. 必做部分【题目1】 甲、乙两人投篮命中的概率分别为23与12，各自相互独立.现两人做投篮游戏，共比赛3局，每局每人各投一球.(1)求比赛结束后甲的进球数比乙的进球数多1个的概率；(2)设ξ表示比赛结束后甲、乙两人进球数的差的绝对值，求ξ的分布列和数学期望E (ξ). 解 (1)比赛结束后甲的进球数比乙的进球数多1个有以下几种情况： 甲进1球，乙进0球；甲进2球，乙进1球；甲进3球，乙进2球. 所以比赛结束后甲的进球数比乙的进球数多1个的概率为P ＝C 13×23×()132×()123＋C 23×()232×()13×C 13×()123＋C 33×()233×C 23×()123＝1136.(2)ξ的取值为0，1，2，3，则P(ξ＝0)＝()133×()123＋C13×23×()132×C13×()123＋C23×()232×13×C23×()123＋()233×()123＝724，P(ξ＝1)＝()133×C13×()123＋C13×23×()132×()123＋C13×23×()132×C23×()123＋C23×()232×13×C13×()123＋C23×()232×13×()123＋()233×C23×()123＝1124，P(ξ＝2)＝()133×C23×()123＋C23×()232×13×()123＋C13×23×()132×()123＋()233×C13×()123＝524，P(ξ＝3)＝()133×()123＋()233×()123＝124，所以ξ的分布列为所以数学期望E(ξ)＝0×724＋1×1124＋2×524＋3×124＝1.【题目2】在(1＋x＋x2)n＝D0n＋D1n x＋D2n x2＋…＋D r n x r＋…＋D2n－1n x2n－1＋D2n n x2n的展开式中，把D0n，D1n，D2n，…，D2n n叫做三项式系数.(1)当n＝2时，写出三项式系数D02，D12，D22，D32，D42的值；(2)类比二项式系数性质C m n＋1＝C m－1n＋C m n(1≤m≤n，m∈N，n∈N)，给出一个关于三项式系数D m＋1n＋1(1≤m≤2n－1，m∈N，n∈N)的相似性质，并予以证明.解(1)因为(1＋x＋x2)2＝1＋2x＋3x2＋2x3＋x4，所以D02＝1，D12＝2，D22＝3，D32＝2，D42＝1.(2)类比二项式系数性质C m n＋1＝C m－1n＋C m n(1≤m≤n，m∈N，n∈N)，三项式系数有如下性质：D m＋1n＋1＝D m－1n＋D m n＋D m＋1n(1≤m≤2n－1).证明如下：因为(1＋x＋x2)n＋1＝(1＋x＋x2)·(1＋x＋x2)n，所以(1＋x ＋x 2)n ＋1＝(1＋x ＋x 2)·(D 0n ＋D 1n x ＋D 2n x 2＋…＋D 2n －1n x 2n －1＋D 2n nx 2n ). 上式左边x m＋1的系数为D m ＋1n ＋1，上式右边xm＋1的系数为D m ＋1n ＋D m n ＋D m －1n ，于是D m ＋1n ＋1＝D m －1n ＋D m n ＋D m ＋1n (1≤m ≤2n －1).专题二请同学从下面所给的三题中选定两题作答 【题目1】 选修4－2：矩阵与变换已知曲线C ：y 2＝12x ，在矩阵M ＝⎣⎡⎦⎤1 00 －2对应的变换作用下得到曲线C 1，C 1在矩阵N ＝⎣⎡⎦⎤0 11 0对应的变换作用下得到曲线C 2，求曲线C 2的方程. 解 设A ＝NM ，则A ＝⎣⎡⎦⎤0 110⎣⎡⎦⎤1－2＝⎣⎡⎦⎤0 －210，设P (x ′，y ′)是曲线C 上任一点，在两次变换下，在曲线C 2上对应的点为P (x ，y )，则⎣⎡⎦⎤xy ＝⎣⎡⎦⎤0 －21 0⎣⎡⎦⎤x ′y ′＝⎣⎡⎦⎤－2y ′ x ′，即⎩⎨⎧x ＝－2y ′，y ＝x ′，∴⎩⎨⎧x ′＝y ，y ′＝－12x . 又点P (x ′，y ′)在曲线C ：y 2＝12x 上，∴()－12x2＝12y ，即x 2＝2y . 【题目2】 选修4－4：坐标系与参数方程 在平面直角坐标系xOy 中，圆的参数方程为⎩⎨⎧x ＝2＋2cos α，y ＝2sin α(α为参数)，以坐标原点O 为极点，x 轴的正半轴为极轴建立极坐标系.求： (1)圆的普通方程； (2)圆的极坐标方程.解 (1)根据sin 2α＋cos 2α＝1，得(x －2)2＋y 2＝4cos 2α＋4sin 2α， 所以圆的普通方程为(x －2)2＋y 2＝4.(2)把⎩⎨⎧x ＝ρcos θ，y ＝ρsin θ代入圆的普通方程得圆的极坐标方程为ρ＝4cos θ.必做部分【题目1】 如图，在多面体ABCDEF 中，ABCD 为正方形，ED ⊥平面ABCD ，FB ∥ED ，且AD ＝DE ＝2BF ＝2.(1)求证：AC ⊥EF ；(2)求二面角C －EF －D 的大小.(1)证明 连接BD ，∵FB ∥ED ，∴F ，B ，E ，D 共面，∵ED ⊥平面ABCD ，AC 平面ABCD ，∴ED ⊥AC ，又ABCD 为正方形， ∴BD ⊥AC ，而ED ∩DB ＝D ，ED ，DB 平面DBFE ，∴AC ⊥平面DBFE ，而EF平面DBFE ，∴AC ⊥EF .(2)解 如图建立空间直角坐标系.则A (2，0，0)，B (2，2，0)，C (0，2，0)，F (2，2，1)，E (0，0，2)， 由(1)知AC →为平面DBFE 的法向量，即AC →＝(－2，2，0)，又CE →＝(0，－2，2)，CF →＝(2，0，1)，设平面CEF 的法向量为n ＝(x ，y ，z )， 则有⎩⎪⎨⎪⎧CE →·n ＝0，CF →·n ＝0，即⎩⎨⎧－2y ＋2z ＝0，2x ＋z ＝0，取z ＝1，则x ＝－12，y ＝1，∴n ＝()－12，1，1.设二面角C －EF －D 的大小为θ，则cos 〈n ，AC →〉＝n ·AC →|n ||AC →|＝1＋232×22＝22，又二面角C －EF －D 为锐角，所以θ＝π4.【题目2】 已知k ，m ∈N *，若存在互不相等的正整数a 1，a 2，…，a m ，使得a 1a 2，a 2a 3，…，a m －1a m ，a m a 1同时小于k ，则记f (k )为满足条件的m 的最大值. (1)求f (6)的值；(2)对于给定的正整数n (n ＞1)，(ⅰ)当n (n ＋2)＜k ≤(n ＋1)(n ＋2)时，求f (k )的解析式； (ⅱ)当n (n ＋1)＜k ≤n (n ＋2)时，求f (k )的解析式. 解 (1)由题意，取a 1＝1，a 2＝2，a 1a 2＜6，满足题意， 若a 3≥3，则必有a 2a 3≥6，不满足题意，综上所述，m 的最大值为2，即f (6)＝2. (2)由题意，当n (n ＋1)＜k ≤(n ＋1)(n ＋2)时，设A 1＝{1，2，…，n }，A 2＝{n ＋1，n ＋2，n ＋3，…}， 显然，a i ，a i ＋1∈A 1时，满足a i a i ＋1≤n (n －1)＜n (n ＋1)＜k ，所以从集合A 1中选出的a i 至多有n 个，a j ，a j ＋1∈A 2时，a j a j ＋1≥(n ＋1)(n ＋2)≥k ，不符合题意， 所以从集合A 2中选出的a j 必不相邻， 又因为从集合A 1中选出的a i 至多有n 个，所以从集合A 2中选出的a j 至多有n 个，放置于从集合A 1中选出的a i 之间， 所以f (k )≤2n .(ⅰ)当n (n ＋2)＜k ≤(n ＋1)(n ＋2)时，取一串数a i 为：1，2n ，2，2n －1，3，2n －2，…，n －1，n ＋2，n ，n ＋1，或写成a i ＝⎩⎪⎨⎪⎧i ＋12，i 为奇数，2n ＋1－i2，i 为偶数(1≤i ≤2n )，此时a i a i ＋1≤n (n ＋2)＜k (1≤i ≤2n －1)，a 2n a 1＝n ＋1＜k ，满足题意，所以f (k )＝2n . (ⅱ)当n (n ＋1)＜k ≤n (n ＋2)时，从A 1中选出的n 个a i ：1，2，…，n ，考虑数n 的两侧的空位，填入集合A 2的两个数a p ，a q ，不妨设na p ＞na q ，则na p ≥n (n ＋2)≥k ，与题意不符， 所以f (k )≤2n －1，取一串数a i 为1，2n －1，2，2n －2，3，2n －3，…，n －2，n ＋2，n －1，n ＋1，n 或写成a i ＝⎩⎪⎨⎪⎧i ＋12，i 为奇数，2n －i 2，i 为偶数(1≤i ≤2n－1)，此时a i a i ＋1≤n (n ＋1)＜k (1≤i ≤2n －2)，a 2n －1a 1＝n ＜k ，满足题意， 所以f (k )＝2n －1.专题三请同学从下面所给的三题中选定两题作答 【题目1】 选修4－2：矩阵与变换 设二阶矩阵A ，B 满足A －1＝⎣⎡⎦⎤1 234，(BA )－1＝⎣⎡⎦⎤1 01，求B －1.解 设B －1＝⎣⎡⎦⎤a bcd ，因为(BA )－1＝A －1B －1，所以⎣⎡⎦⎤1 01＝⎣⎡⎦⎤1 23 4⎣⎡⎦⎤a b c d ， 即⎩⎪⎨⎪⎧a ＋2c ＝1，b ＋2d ＝0，3a ＋4c ＝0，3b ＋4d ＝1，解得⎩⎪⎨⎪⎧a ＝－2，b ＝1，c ＝32，d ＝－12，所以B－1＝⎣⎢⎡⎦⎥⎤－2 132 －12.【题目2】 选修4－4：坐标系与参数方程在极坐标系中，已知曲线C ：ρ＝2sin θ，过极点O 的直线l 与曲线C 交于A ，B 两点，且AB ＝3，求直线l 的方程.解 设直线l 的方程为θ＝θ0(ρ∈R )，A (0，0)，B (ρ1，θ0)，则AB ＝|ρ1－0|＝|2sin θ0|.又AB ＝3，故sin θ0＝±32. 解得θ0＝π3＋2k π或θ0＝－π3＋2k π，k ∈Z .所以直线l 的方程为θ＝π3或θ＝2π3(ρ∈R ).【题目3】 选修4－5：不等式选讲 已知a ≥0，b ≥0，求证：a 6＋b 6≥ab (a 4＋b 4).证明 ∵a 6＋b 6－ab (a 4＋b 4)＝a 5(a －b )－(a －b )b 5＝(a －b )(a 5－b 5). 又a ≥0，b ≥0，当a －b ≥0时，a 5－b 5≥0； 当a －b ＜0时，a 5－b 5＜0，即(a －b )(a 5－b 5)≥0， 所以a 6＋b 6－ab (a 4＋b 4)≥0，即a 6＋b 6≥ab (a 4＋b 4).必做部分【题目1】 某校高一、高二两个年级进行乒乓球对抗赛，每个年级选出3名学生组成代表队，比赛规则是：①按“单打、双打、单打”顺序进行三盘比赛；②代表队中每名队员至少参加一盘比赛，但不能参加两盘单打比赛.若每盘比赛中高一、高二获胜的概率分别为37，47.(1)按比赛规则，高一年级代表队可以派出多少种不同的出场阵容？(2)若单打获胜得2分，双打获胜得3分，求高一年级得分ξ的概率分布列和数学期望.解 (1)先安排参加单打的队员有A 23种方法，再安排参加双打的队员有C 12种方法，所以，高一年级代表队出场共有A 23C 12＝12种不同的阵容.(2)ξ的取值可能是0，2，3，4，5，7. P (ξ＝0)＝()1－373＝64343，P (ξ＝2)＝C 12×37×()1－372＝96343， P (ξ＝3)＝()1－372×37＝48343，P (ξ＝4)＝()372×()1－37＝36343，P (ξ＝5)＝C 12×37×()1－37×37＝72343，P (ξ＝7)＝()373＝27343， ξ的概率分布列为所以E (ξ)＝0×64343＋2×96343＋3×48343＋4×36343＋5×72343＋7×27343＝3.【题目2】 已知抛物线C ：x 2＝2py (p ＞0)过点(2，1)，直线l 过点P (0，－1)与抛物线C 交于A ，B 两点.点A 关于y 轴的对称点为A ′，连接A ′B .(1)求抛物线C 的标准方程；(2)问直线A ′B 是否过定点？若是，求出定点坐标；若不是，请说明理由. 解 (1)将点(2，1)代入抛物线C 的方程得p ＝2， 所以抛物线C 的标准方程为x 2＝4y .(2)设直线l 的方程为y ＝kx －1，又设A (x 1，y 1)，B (x 2，y 2)，则A ′(－x 1，y 1)，由⎩⎨⎧y ＝14x 2，y ＝kx －1得x 2－4kx ＋4＝0，则Δ＝16k 2－16＞0， x 1＝2k －2k 2－1，x 2＝2k ＋2k 2－1， 所以k A ′B ＝y 2－y 1x 2－（－x 1）＝x 224－x 214x 1＋x 2＝x 2－x 14，于是直线A ′B 的方程为y －x 224＝x 2－x 14(x －x 2)，所以y ＝x 2－x 14(x －x 2)＋x 224＝k 2－1x ＋1，当x ＝0时，y ＝1，所以直线A ′B 过定点(0，1).专题4请同学从下面给的三题中选定两题作答 【题目1】 选修4－2：矩阵与变换 已知矩阵A ＝⎣⎡⎦⎤1 2cd (c ，d 为实数).若矩阵A 属于特征值2，3的一个特征向量分别为⎣⎡⎦⎤21，⎣⎡⎦⎤11，求矩阵A 的逆矩阵A －1.解 由题意知⎣⎡⎦⎤1 2cd ⎣⎡⎦⎤21＝⎣⎡⎦⎤ 42c ＋d ＝2⎣⎡⎦⎤21，⎣⎡⎦⎤1 2c d ⎣⎡⎦⎤11＝⎣⎡⎦⎤ 3c ＋d ＝3⎣⎡⎦⎤11，所以⎩⎨⎧2c ＋d ＝2，c ＋d ＝3，解得⎩⎨⎧c ＝－1，d ＝4.所以A ＝⎣⎡⎦⎤1 2－1 4，所以A －1＝⎣⎢⎢⎡⎦⎥⎥⎤23－131616.【题目2】 选修4－4：坐标系与参数方程已知直线l 的极坐标方程为ρsin ()θ－π3＝3，曲线C 的参数方程为⎩⎨⎧x ＝2cos θ，y ＝2sin θ(θ为参数)，设点P 是曲线C 上的任意一点，求P 到直线l 的距离的最大值.解 由ρsin ()θ－π3＝3，可得ρ⎝⎛⎭⎫12sin θ－32cos θ＝3.所以y －3x ＝6，即3x －y ＋6＝0，由⎩⎨⎧x ＝2cos θ，y ＝2sin θ得x 2＋y 2＝4，圆的半径为r ＝2，所以圆心到直线l 的距离d ＝62＝3，所以P 到直线l 的距离的最大值为d ＋r ＝5.【题目3】 选修4－5：不等式选讲已知x ，y ，z ∈R ，且x ＋2y ＋3z ＋8＝0.求证：(x －1)2＋(y ＋2)2＋(z －3)2≥14. 证明 因为[(x －1)2＋(y ＋2)2＋(z －3)2](12＋22＋32)≥[(x －1)＋2(y ＋2)＋3(z －3)]2 ＝(x ＋2y ＋3z －6)2＝142，当且仅当x －11＝y ＋22＝z －33，即x ＝z ＝0，y ＝－4时，取等号， 所以(x －1)2＋(y ＋2)2＋(z －3)2≥14.必做部分【题目1】 如图，在直三棱柱ABC －A 1B 1C 1中，已知CA ＝CB ＝1，AA 1＝2，∠BCA ＝90°.(1)求异面直线BA 1与CB 1夹角的余弦值； (2)求二面角B －AB 1－C 平面角的余弦值.解 如图，以{CA →，CB →，CC 1→}为正交基底，建立空间直角坐标系C －xyz ，则A (1，0，0)，B (0，1，0)，A 1(1，0，2)，B 1(0，1，2)，所以CB 1→＝(0，1，2)，AB →＝(－1，1，0)，AB 1→＝(－1，1，2)，BA 1→＝(1，－1，2). (1)因为cos 〈CB 1→，BA 1→〉＝CB 1→·BA 1→|CB 1→||BA 1→|＝35×6＝3010，所以异面直线BA 1与CB 1夹角的余弦值为3010. (2)设平面CAB 1的法向量为m ＝(x ，y ，z )，则⎩⎪⎨⎪⎧m ·AB 1→＝0，m ·CB 1→＝0，即⎩⎨⎧－x ＋y ＋2z ＝0，y ＋2z ＝0，取平面CAB 1的一个法向量为m ＝(0，2，－1)；设平面BAB 1的法向量为n ＝(r ，s ，t )，则⎩⎪⎨⎪⎧n ·AB 1→＝0，n ·AB →＝0，即⎩⎨⎧－r ＋s ＋2t ＝0，－r ＋s ＝0，取平面BAB 1的一个法向量为n ＝(1，1，0)，则cos 〈m ，n 〉＝m·n|m ||n |＝25×2＝105，易知二面角B －AB 1－C 为锐角，所以二面角B －AB 1－C 平面角的余弦值为105. 【题目2】 在数列{a n }中，已知a 1＝20，a 2＝30，a n ＋1＝3a n －a n －1(n ∈N *，n ≥2).(1)当n ＝2，3时，分别求a 2n －a n －1a n ＋1的值，并判断a 2n －a n －1a n ＋1(n ≥2)是否为定值，然后给出证明；(2)求出所有的正整数n ，使得5a n ＋1a n ＋1为完全平方数.解 (1)由已知得a 3＝70，a 4＝180.所以当n ＝2时，a 2n －a n －1a n ＋1＝－500；当n ＝3时，a 2n －a n －1a n ＋1＝－500.猜想：a 2n－a n －1a n ＋1＝－500(n ≥2). 下面用数学归纳法证明： ①当n ＝2时，结论成立.②假设当n ＝k (k ≥2，k ∈N *)时，结论成立，即a 2k －a k －1a k ＋1＝－500. 将a k ＋1＝3a k －a k －1代入上式，可得a 2k －3a k a k ＋1＋a 2k ＋1＝－500.则当n ＝k ＋1时，a 2k ＋1－a k a k ＋2＝a 2k ＋1－a k (3a k ＋1－a k )＝a 2k ＋1－3a k a k ＋1＋a 2k ＝－500.故当n ＝k ＋1结论成立，根据①②可得a 2n －a n －1a n ＋1＝－500(n ≥2)成立. (2)将a n －1＝3a n －a n ＋1代入a 2n －a n －1a n ＋1＝－500，得a 2n ＋1－3a n a n ＋1＋a 2n ＝－500，则5a n ＋1a n ＝(a n ＋1＋a n )2＋500，5a n a n ＋1＋1＝(a n ＋1＋a n )2＋501， 设5a n ＋1a n ＋1＝t 2(t ∈N *)，则t 2－(a n ＋1＋a n )2＝501，即[t －(a n ＋1＋a n )](t ＋a n ＋1＋a n )＝501， 又a n ＋1＋a n ∈N ，且501＝1×501＝3×167， 故⎩⎨⎧a n ＋1＋a n －t ＝－1，a n ＋1＋a n ＋t ＝501或⎩⎨⎧a n ＋1＋a n －t ＝－3，a n ＋1＋a n ＋t ＝167， 所以⎩⎨⎧t ＝251，a n ＋1＋a n ＝250或⎩⎨⎧t ＝85，a n ＋1＋a n ＝82，由a n ＋1＋a n ＝250解得n ＝3；由a n ＋1＋a n ＝82得n 无整数解，所以当n ＝3时，满足条件.专题五2.(2018·江苏省盐城中学调研)已知矩阵M ＝⎣⎡⎦⎤0 ab 0满足：Ma i ＝λi a i ，其中λi (i ＝1,2)是互不相等的实常数，a i (i ＝1,2)是非零的平面列向量，λ1＝1，a 2＝⎣⎡⎦⎤11，求矩阵M .解由题意，λ1，λ2是方程f (λ)＝⎪⎪⎪⎪⎪⎪ λ－a －bλ＝λ2－ab ＝0的两根. 因为λ1＝1，所以ab ＝1.又因为Ma 2＝λ2a 2，所以⎣⎡⎦⎤0 a b 0 ⎣⎡⎦⎤11＝λ2⎣⎡⎦⎤11，从而⎩⎨⎧a ＝λ2，b ＝λ2，所以λ22＝ab ＝1.因为λ1≠λ2，所以λ2＝－1，从而a ＝b ＝－1，故矩阵M ＝⎣⎢⎡⎦⎥⎤ 0 －1－10. 3.(2018·苏州、南通等六市模拟)在极坐标系中，求以点P ()2，π3为圆心且与直线l: ρsin ()θ－π3＝2相切的圆的极坐标方程.解 以极点为原点，极轴为x 轴的正半轴，建立平面直角坐标系xOy .则点P 的直角坐标为()1，3.将直线l: ρsin ()θ－π3＝2的方程变形为： ρsin θcos π3－ρcos θsin π3＝2，化为普通方程得3x －y ＋4＝0.∴P ()1，3到直线l: 3x －y ＋4＝0的距离为4()32＋()－12＝2.∴所求圆的普通方程为()x －12＋()y －32＝4，化为极坐标方程得ρ＝4sin ()θ＋π6.4.已知实数x >0，y >0，z >0，证明：()1x ＋2y ＋3z ()x 2＋y 4＋z 6≥92. 证明 因为x >0，y >0，z >0， 所以1x ＋2y ＋3z 3≥36xyz ，x 2＋y 4＋z 63≥ 3xyz 48， 所以()1x ＋2y ＋3z()x 2＋y 4＋z 6≥92. 当且仅当x ∶y ∶z ＝1∶2∶3时，等号成立. 5.已知点A (1,2)在抛物线F ：y 2＝2px 上.(1)若△ABC 的三个顶点都在抛物线F 上，记三边AB ，BC ，CA 所在直线的斜率分别为k 1，k 2，k 3, 求1k 1－1k 2＋1k 3的值；(2)若四边形ABCD 的四个顶点都在抛物线F 上，记四边AB ，BC ，CD ，DA 所在直线的斜率分别为k 1，k 2，k 3，k 4，求1k 1－1k 2＋1k 3－1k 4的值. 解 (1)由点A (1,2)在抛物线F 上，得p ＝2， ∴抛物线F ：y 2＝4x ， 设B ()y 214，y 1，C ()y 224，y 2， ∴1k 1－1k 2＋1k 3＝y 214－1y 1－2－y 224－y 214y 2－y 1＋1－y 2242－y 2＝y 1＋24－y 2＋y 14＋2＋y 24＝1. (2)另设D ()y 234，y 3，则1k 1－1k 2＋1k 3－1k 4＝y 1＋24－y 2＋y 14＋y 3＋y 24－2＋y 34＝0.6.已知f n (x )＝C 0n x n －C 1n (x －1)n ＋…＋(－1)k C k n (x －k )n ＋…＋(－1)n C n n (x －n )n ，其中x ∈R ，n ∈N *，k ∈N ，k ≤n .(1)试求f 1(x )，f 2(x )，f 3(x )的值；(2)试猜测f n (x )关于n 的表达式，并证明你的结论.解 (1)f 1(x )＝C 01x －C 11(x －1)＝1，f 2(x )＝C 02x 2－C 12(x －1)2＋C 22(x －2)2＝x 2－2(x －1)2＋(x －2)2＝2，f 3(x )＝C 03x 3－C 13(x －1)3＋C 23(x －2)3－C 33(x －3)3＝x 3－3(x －1)3＋3(x －2)3－(x －3)3＝6.(2)猜测f n (x )＝n ！，n ∈N *. 以下用数学归纳法证明.①当n ＝1时，f 1(x )＝1，等式成立.②假设当n ＝m (m ≥1，m ∈N *)时，等式成立，即f m (x )＝∑k ＝0m(－1)k C k m(x －k )m ＝m ！. 当n ＝m ＋1时，则f m ＋1(x )＝∑k ＝0m ＋1(－1)k C k m ＋1·(x －k )m ＋1. 因为C k m ＋1＝C k m ＋C k －1m ，k C k m ＋1＝(m ＋1)·C k －1m，其中k ＝1,2，…，m ， 且C 0m ＋1＝C 0m ，C m ＋1m ＋1＝C m m ， 所以f m ＋1(x )＝∑k ＝0m ＋1(－1)k C k m ＋1(x －k )m ＋1＝x ∑k ＝0m ＋1(－1)k C k m ＋1(x －k )m－∑k ＝0m ＋1(－1)k k C km ＋1(x －k )m＝x ∑k ＝0m(－1)k C k m(x －k )m ＋x ∑k ＝1m ＋1(－1)k C k －1m(x －k )m －(m ＋1)∑k ＝1m ＋1(－1)k C k－1m (x －k )m ＝x ·m ！＋(－x ＋m ＋1)∑k ＝0m(－1)k C k m ·[(x －1)－k ]m ＝x ·m ！＋(－x ＋m ＋1)·m!＝(m ＋1)·m ！＝(m ＋1)！. 即当n ＝m ＋1时，等式也成立. 由①②可知，对n ∈N *，均有f n (x )＝n ！.专题六2.(2018·苏州、南通等六市模拟)在平面直角坐标系xOy 中，已知A ()0，0，B ()3，0，C ()2，2.设变换T 1, T 2对应的矩阵分别为M ＝⎣⎡⎦⎤1 02， N ＝⎣⎡⎦⎤2 00 1，求对△ABC 依次实施变换T 1, T 2后所得图形的面积.解 依题意，依次实施变换T 1, T 2所对应的矩阵NM ＝ ⎣⎡⎦⎤2 01 ⎣⎡⎦⎤1 00 2＝⎣⎡⎦⎤2 00 2.则⎣⎡⎦⎤2 02 ⎣⎡⎦⎤00＝⎣⎡⎦⎤00， ⎣⎡⎦⎤2 00 2 ⎣⎡⎦⎤30＝⎣⎡⎦⎤60，⎣⎡⎦⎤2 00 2 ⎣⎡⎦⎤22＝⎣⎡⎦⎤44.∴A ()0，0，B ()3，0，C ()2，2分别变为点A ′()0，0，B ′()6，0，C ′()4，4. ∴所得图形的面积为12×6×4＝12.3.已知两个动点P ，Q 分别在两条直线l 1：y ＝x 和l 2：y ＝－x 上运动，且它们的横坐标分别为角θ的正弦，余弦，θ∈[0，π]，记OM →＝OP →＋OQ →，求动点M 的轨迹的普通方程.解设M (x ，y )，则⎩⎨⎧x ＝sin θ＋cos θ，y ＝sin θ－cos θ，两式平方相加得x 2＋y 2＝2.又x ＝2sin ()θ＋π4，y ＝2sin ()θ－π4， θ∈[0，π]， 所以x ∈[－1，2]，y ∈[－1，2].所以动点M 轨迹的普通方程为x 2＋y 2＝2(x ，y ∈[－1，2]).4.(2018·江苏省盐城中学质检)已知a >0，b >0，证明：(a 2＋b 2＋ab )(ab 2＋a 2b ＋1)≥9a 2b 2.证明 因为a >0，b >0，所以a 2＋b 2＋ab ≥33a 2·b 2·ab ＝3ab >0，ab 2＋a 2b ＋1≥33ab 2·a 2b ·1＝3ab >0， 所以(a 2＋b 2＋ab )(ab 2＋a 2b ＋1)≥9a 2b 2.5.甲、乙两人轮流投篮，每人每次投一次篮，先投中者获胜，投篮进行到有人获胜或每人都已投球3次时结束.设甲每次投篮命中的概率为25，乙每次投篮命中的概率为23，且各次投篮互不影响.现由甲先投.(1)求甲获胜的概率；(2)求投篮结束时甲的投篮次数X 的概率分布与数学期望.解 (1)设甲第i 次投中获胜的事件为A 1(i ＝1,2,3)，则A 1，A 2，A 3彼此互斥. 甲获胜的事件为A 1＋A 2＋A 3. P (A 1)＝25，P (A 2)＝35×13×25＝225，P (A 3)＝()352×()132×25＝2125. 所以P (A 1＋A 2＋A 3)＝P (A 1)＋P (A 2)＋P (A 3)＝25＋225＋2125＝62125.(2)X 的所有可能取值为1,2,3. 则P (X ＝1)＝25＋35×23＝45，P (X ＝2)＝225＋35×13×35×23＝425，P (X ＝3)＝()352×()132×1＝125. 即X 的概率分布为所以数学期望E (X )＝1×45＋2×425＋3×125＝3125.6.设n 个正数a 1，a 2，…，a n 满足a 1≤a 2≤…≤a n (n ∈N *且n ≥3). (1)当n ＝3时，证明：a 1a 2a 3＋a 2a 3a 1＋a 3a 1a 2≥a 1＋a 2＋a 3；(2)当n ＝4时，不等式a 1a 2a 3＋a 2a 3a 4＋a 3a 4a 1＋a 4a 1a 2≥a 1＋a 2＋a 3＋a 4也成立，请你将其推广到n (n ∈N *且n ≥3)个正数a 1，a 2，…，a n 的情形，归纳出一般性的结论并用数学归纳法证明. 证明 (1)因为a n (n ∈N *且n ≥3)均为正实数，左—右＝12()a 1a 3a 2＋a 1a 2a 3－2a 1＋12()a 2a 3a 1＋a 1a 2a 3－2a 2＋12()a 2a 3a 1＋a 1a 3a 2－2a 3≥12⎝⎛⎭⎫2a 1a 3a 2×a 1a 2a 3－2a 1＋12⎝⎛⎭⎫2a 2a 3a 1×a 1a 2a 3－2a 2＋12⎝⎛⎭⎫2a 2a 3a 1×a 1a 3a 2－2a 3＝0， 所以原不等式a 2a 3a 1＋a 1a 3a 2＋a 1a 2a 3≥a 1＋a 2＋a 3成立. (2)归纳的不等式为：a 1a 2a 3＋a 2a 3a 4＋…＋a n －2a n －1a n ＋a n －1a n a 1＋a n a 1a 2≥a 1＋a 2＋…＋a n (n ∈N *且n ≥3). 记F n ＝a 1a 2a 3＋a 2a 3a 4＋…＋a n －2a n －1a n ＋a n －1a n a 1＋a n a 1a 2－(a 1＋a 2＋…＋a n )， 当n ＝3(n ∈N *)时，由(1)知，不等式成立； 假设当n ＝k (k ∈N *且k ≥3)时，不等式成立，即F k ＝a 1a 2a 3＋a 2a 3a 4＋…＋a k －2a k －1a k ＋a k －1a k a 1＋a k a 1a 2－(a 1＋a 2＋…＋a k )≥0. 则当n ＝k ＋1时，F k ＋1＝a 1a 2a 3＋a 2a 3a 4＋…＋a k －2a k －1a k ＋a k －1a k a k ＋1＋a k a k ＋1a 1＋a k ＋1a 1a 2－(a 1＋a 2＋…＋a k ＋a k ＋1) ＝F k ＋a k －1a k a k ＋1＋a k a k ＋1a 1＋a k ＋1a 1a 2－a k －1a k a 1－a k a 1a 2－a k ＋1＝F k ＋a k －1a k ⎝⎛⎭⎫1ak ＋1－1a 1＋a k ＋1()a k a 1－1＋a 1a 2(a k ＋1－a k )≥0＋a 2k ⎝⎛⎭⎫1a k ＋1－1a 1＋a k ＋1()a k a 1－1＋a 1a k (a k ＋1－a k )＝(a k ＋1－a k )⎝ ⎛⎭⎪⎫a k a 1＋a 1a k －a k ＋1＋a k a k ＋1， 因为a k ＋1≥a k ，a k a 1＋a 1a k ≥2，a k ＋1＋a k a k ＋1≤a k ＋1＋a k ＋1a k ＋1＝2，所以F k ＋1≥0，所以当n ＝k ＋1时，不等式成立.综上所述，不等式a 1a 2a 3＋a 2a 3a 4＋…＋a n －2a n －1a n ＋a n －1a n a 1＋a n a 1a 2≥a 1＋a 2＋…＋a n (n ∈N *且n ≥3)成立.专题七2.若二阶矩阵M 满足⎣⎢⎡⎦⎥⎤－2122－1M ＝⎣⎡⎦⎤－3 0 4－1，求曲线4x 2＋4xy ＋y 2－12x ＋12y ＝0在矩阵M 所对应的变换作用下得到的曲线的方程.解记矩阵A ＝⎣⎢⎢⎡⎦⎥⎥⎤－2122 －1，det(A )＝(－2)×(－1)－2×12＝1≠0，故A －1＝⎣⎢⎢⎡⎦⎥⎥⎤－1 －12－2 －2，所以M ＝A －1⎣⎢⎡⎦⎥⎤－30 4 －1＝⎣⎢⎢⎡⎦⎥⎥⎤－1－12－2－2 ⎣⎢⎡⎦⎥⎤－30 4－1＝⎣⎢⎢⎡⎦⎥⎥⎤ 112－22，即矩阵M ＝⎣⎢⎢⎡⎦⎥⎥⎤ 112－2 2.设曲线4x 2＋4xy ＋y 2－12x ＋12y ＝0上任意一点P (x ，y )在矩阵M 对应的变换作用下得到点P ′(x ′，y ′).所以⎣⎡⎦⎤x ′y ′＝⎣⎢⎢⎡⎦⎥⎥⎤ 112－22 ⎣⎡⎦⎤x y ＝⎣⎢⎢⎡⎦⎥⎥⎤ x ＋12y －2x ＋2y ， 所以⎩⎪⎨⎪⎧x ′＝x ＋12y ，y ′＝－2x ＋2y ，所以⎩⎨⎧x ＝4x ′－y ′6，y ＝2x ′＋y ′3，又点P (x ，y )在曲线4x 2＋4xy ＋y 2－12x ＋12y ＝0上，代入整理得2x ′2＋3y ′＝0， 由点P (x ，y )的任意性可知，所求曲线的方程为2x 2＋3y ＝0.3.已知直线的极坐标方程为ρsin ()θ＋π4＝22，圆M 的参数方程为⎩⎨⎧x ＝2cos θ，y ＝－2＋2sin θ(其中θ为参数).(1)将直线的极坐标方程化为直角坐标方程； (2)求圆M 上的点到直线的距离的最小值. 解 (1)极点为直角坐标原点O ，ρsin ()θ＋π4＝ρ⎝⎛⎭⎫22sin θ＋22cos θ＝22，∴ρsin θ＋ρcos θ＝1，其直角坐标方程为x ＋y －1＝0.(2)将圆的参数方程化为普通方程为x 2＋(y ＋2)2＝4，圆心为M (0，－2)，∴点M 到直线的距离为d ＝|0－2－1|2＝32＝322，∴圆上的点到直线距离的最小值为32－42.4.已知函数f (x )＝|x ＋m |＋|x －2|(m >0)的最小值为4，正实数a ，b 满足1a ＋1b ＝ 3.求证：1a 2＋2b2≥m .证明 易知|x ＋m |＋|x －2|≥|(x ＋m )－(x －2)|＝|m ＋2|， 故由f (x )的最小值为4得|m ＋2|＝4，又m >0，所以m ＝2. 又()1a 2＋2b 2⎣⎡⎦⎤12＋⎝⎛⎭⎫122≥⎝⎛⎭⎫1a ×1＋2b ×122＝3，当且仅当a ＝32，b ＝3时等号成立，故1a 2＋2b2≥2＝m ，即结论成立. 5.如图，在直三棱柱ABC －A 1B 1C 1中，AA 1＝AB ＝AC ＝2，AB ⊥AC ，M 是棱BC 的中点，点P 在线段A 1B 上.(1)若P 是线段A 1B 的中点，求直线MP 与直线AC 所成角的大小；(2)若N 是CC 1的中点，直线A 1B 与平面PMN 所成角的正弦值为77，求线段BP 的长度. 解 分别以AB ，AC ，AA 1所在直线为x 轴，y 轴，z 轴，建立如图所示的空间直角坐标系，则A (0,0,0)，B (2,0,0)，C (0,2,0)，A 1(0,0,2)，M (1,1,0).(1)若P 是线段A 1B 的中点，则P (1,0,1)，MP →＝(0，－1,1)，AC →＝(0,2,0). 所以cos 〈MP →，AC →〉＝MP →·AC →||MP →·||AC→＝－22.又〈MP →，AC →〉∈[0，π]，所以〈MP →，AC →〉＝3π4.所以直线MP 与直线AC 所成的角的大小为π4.(2)由N (0,2,1)，得MN →＝(－1,1,1). 设P (x ，y ，z )，BP →＝λBA 1,0≤λ≤1，则(x －2，y ，z )＝λ(－2,0,2)，所以⎩⎨⎧x ＝2－2λ，y ＝0，z ＝2λ，所以P (2－2λ，0,2λ)，所以MP →＝(1－2λ，－1,2λ). 设平面PMN 的法向量n ＝(x 1，y 1，z 1)， 则n ⊥MN →，n ⊥MP →，所以⎩⎨⎧－x 1＋y 1＋z 1＝0，(1－2λ)x 1－y 1＋2λz 1＝0，取n ＝()1＋12λ，12λ，1.因为BA 1＝(－2,0,2)，设直线A 1B 与平面PMN 所成的角为θ.由sin θ＝||cos 〈n ，BA 1〉＝|n ·BA 1|||n ·||BA 1＝⎪⎪⎪⎪(－2)×()1＋12λ＋2()1＋12λ2＋()12λ2＋1·22＝77，得λ＝14(舍负). 所以BP →＝14BA 1，所以BP ＝14BA 1＝22.6.已知()1＋12xn展开式的各项依次记为a 1(x )，a 2(x )，a 3(x )，…，a n(x )，an ＋1(x ).设F (x )＝a 1(x )＋2a 2(x )＋3a 3(x )＋…＋na n (x )＋(n ＋1)·a n ＋1(x ).(1)若a 1(x )，a 2(x )，a 3(x )的系数依次成等差数列，求n 的值； (2)求证：对任意x 1，x 2∈[0,2]，恒有|F (x 1)－F (x 2)|≤2n －1(n ＋2)－1. (1)解 依题意a k (x )＝C k －1n ()12x k －1，k ＝1,2,3，…，n ＋1，a 1(x )，a 2(x )，a 3(x )的系数依次为C 0n ·()12＝1，C 1n ·12＝n 2，C 2n ·()122＝n (n －1)8， 所以2×n2＝1＋n (n －1)8，解得n ＝8或n ＝1(舍去).(2)证明 F (x )＝a 1(x )＋2a 2(x )＋3a 3(x )＋…＋na n (x )＋(n ＋1)a n ＋1(x )＝C 0n ＋2C 1n ()12x ＋3C 2n()12x 2＋…＋n C n －1n()12x n －1＋(n ＋1)C n n ()12x n，F (2)＝C 0n ＋2C 1n ＋3C 2n ＋…＋n C n －1n ＋(n ＋1)C nn ，设S n ＝C 0n ＋2C 1n ＋3C 2n ＋…＋n C n －1n ＋(n ＋1)C n n ，则S n ＝(n ＋1)C n n ＋n C n －1n ＋…＋3C 2n ＋2C 1n ＋C 0n ，考虑到C k n ＝C n －k n ，将以上两式相加得2S n ＝(n ＋2)(C 0n ＋C 1n ＋C 2n ＋…＋C n －1n ＋C n n )，所以S n ＝2n －1(n ＋2)，又当x ∈[0,2]时，F ′(x )>0恒成立，从而F (x )是[0,2]上的单调递增函数， 所以对任意x 1，x 2∈[0,2]，|F (x 1)－F (x 2)|≤F (2)－F (0)＝2n －1(n ＋2)－1。

选修4－2 矩阵与变换A[最新考纲]1．了解二阶矩阵的概念，了解线性变换与二阶矩阵之间的关系．2．了解旋转变换、反射变换、伸缩变换、投影变换、切变变换这五种变换的概念与矩阵表示．3．理解变换的复合与矩阵的乘法；理解二阶矩阵的乘法和简单性质． 4．理解逆矩阵的意义，会求出简单二阶逆矩阵．5．理解矩阵的特征值与特征向量，会求二阶矩阵的特征值与特征向量.知 识 梳 理1．矩阵的乘法规则(1)行矩阵[a 11 a 12]与列矩阵⎣⎢⎢⎡⎦⎥⎥⎤b 11b 21的乘法规则： [a 11 a 12]⎣⎢⎢⎡⎦⎥⎥⎤b 11b 21＝[a 11×b 11＋a 12×b 21]． (2)二阶矩阵⎣⎢⎢⎡⎦⎥⎥⎤a 11a 21 a 12a 22与列向量⎣⎢⎢⎡⎦⎥⎥⎤x 0y 0的乘法规则： ⎣⎢⎢⎡⎦⎥⎥⎤a 11a 21 a 12a 22⎣⎢⎢⎡⎦⎥⎥⎤x 0y 0＝⎣⎢⎢⎡⎦⎥⎥⎤a 11×x 0＋a 12×y 0a 21×x 0＋a 22×y 0. 设A 是一个二阶矩阵，α、β是平面上的任意两个向量，λ、λ1、λ2是任意三个实数，则①A (λα)＝λAα；②A (α＋β)＝Aα＋Aβ； ③A (λ1α＋λ2β)＝λ1Aα＋λ2Aβ.(3)两个二阶矩阵相乘的结果仍然是一个矩阵，其乘法法则如下： ⎣⎢⎢⎡⎦⎥⎥⎤a 11a 21 a 12a 22⎣⎢⎢⎡⎦⎥⎥⎤b 11b 21 b 12b 22＝ ⎣⎢⎢⎡⎦⎥⎥⎤a 11×b 11＋a 12×b 21a 21×b 11＋a 22×b 21 a 11×b 12＋a 12×b 22a 21×b 12＋a 22×b 22 性质：①一般情况下，AB ≠BA ，即矩阵的乘法不满足交换律；②矩阵的乘法满足结合律，即(AB )C ＝A (BC )；③矩阵的乘法不满足消去律． 2．矩阵的逆矩阵(1)逆矩阵的有关概念：对于二阶矩阵A ，B ，若有AB ＝BA ＝E ，则称A 是可逆的，B 称为A 的逆矩阵．若二阶矩阵A 存在逆矩阵B ，则逆矩阵是唯一的，通常记A 的逆矩阵为A －1，A －1＝B .(2)逆矩阵的求法：一般地，对于二阶可逆矩阵A ＝⎣⎢⎡⎦⎥⎤a b c d (det A ＝ad －bc ≠0)，它的逆矩阵为A－1＝⎣⎢⎢⎡⎦⎥⎥⎤dad －bc－b ad －bc －c ad －bc a ad －bc . (3)逆矩阵与二元一次方程组：如果关于变量x ，y 的二元一次方程组⎩⎨⎧ax ＋by ＝m ，cx ＋dy ＝n的系数矩阵A ＝⎣⎢⎡⎦⎥⎤a b c d 可逆，那么该方程组有唯一解⎣⎢⎡⎦⎥⎤x y ＝⎣⎢⎡⎦⎥⎤a b c d －1⎣⎢⎡⎦⎥⎤m n ， 其中A －1＝⎣⎢⎢⎡⎦⎥⎥⎤dad －bc－b ad －bc－c ad －bca ad －bc . 3．二阶矩阵的特征值和特征向量 (1)特征值与特征向量的概念设A 是一个二阶矩阵，如果对于实数λ，存在一个非零向量α，使得Aα＝λα，那么λ称为A 的一个特征值，而α称为A 的一个属于特征值λ的一个特征向量．(2)特征多项式与特征方程 设λ是二阶矩阵A ＝⎣⎢⎡⎦⎥⎤ab c d 的一个特征值，它的一个特征向量为ξ＝⎣⎢⎡⎦⎥⎤x y ，则A ⎣⎢⎡⎦⎥⎤x y ＝λ⎣⎢⎡⎦⎥⎤x y ， 即⎣⎢⎡⎦⎥⎤x y 满足二元一次方程组⎩⎨⎧ax ＋by ＝λx ，cx ＋dy ＝λy ， 故⎩⎨⎧(λ－a )x －by ＝0－cx ＋(λ－d )y ＝0⇔⎣⎢⎡⎦⎥⎤λ－a －b －c λ－d ⎣⎢⎡⎦⎥⎤x y ＝⎣⎢⎡⎦⎥⎤00(*)则(*)式有非零解的充要条件是它的系数矩阵的行列式 ⎪⎪⎪⎪⎪⎪λ－a －b －c λ－d ＝0.记f (λ)＝⎪⎪⎪⎪⎪⎪λ－a －b －c λ－d 为矩阵A ＝⎣⎢⎡⎦⎥⎤a b c d 的特征多项式；方程⎪⎪⎪⎪⎪⎪λ－a －b －c λ－d ＝0，即f (λ)＝0称为矩阵A ＝⎣⎢⎡⎦⎥⎤ab c d 的特征方程． (3)特征值与特征向量的计算如果λ是二阶矩阵A 的特征值，则λ是特征方程f (λ)＝⎪⎪⎪⎪⎪⎪λ－a －b －c λ－d ＝λ2－(a ＋d )λ＋ad －bc ＝0的一个根．解这个关于λ的二元一次方程，得λ＝λ1、λ2，将λ＝λ1、λ2分别代入方程组(*)，分别求出它们的一个非零解⎩⎨⎧ x ＝x 1，y ＝y 1，⎩⎨⎧x ＝x 2，y ＝y 2，记ξ1＝⎣⎢⎡⎦⎥⎤x 1y 1，ξ2＝⎣⎢⎡⎦⎥⎤x 2y 2.则Aξ1＝λ1ξ1、Aξ2＝λ2ξ2，因此λ1、λ2是矩阵A ＝⎣⎢⎡⎦⎥⎤ab cd 的特征值，ξ1＝⎣⎢⎡⎦⎥⎤x 1y 1，ξ2＝⎣⎢⎡⎦⎥⎤x 2y 2为矩阵A 的分别属于特征值λ1、λ2的一个特征向量． 诊 断 自 测1. ⎣⎢⎡⎦⎥⎤1 00 －1 ⎣⎢⎡⎦⎥⎤57＝________.解析 ⎣⎢⎡⎦⎥⎤1 00 －1⎣⎢⎡⎦⎥⎤57＝⎣⎢⎢⎡⎦⎥⎥⎤ 1×5＋0×7 0×5＋(－1)×7＝⎣⎢⎡⎦⎥⎤5－7.答案 ⎣⎢⎡⎦⎥⎤5－72．若A ＝⎣⎢⎢⎡⎦⎥⎥⎤12 121212，B ＝⎣⎢⎢⎡⎦⎥⎥⎤12 －12－1212，则AB ＝________. 解析AB ＝⎣⎢⎢⎡⎦⎥⎥⎤12 1212 12⎣⎢⎢⎡⎦⎥⎥⎤ 12 －12－12 12 ＝⎣⎢⎢⎡⎦⎥⎥⎤12×12＋12×⎝ ⎛⎭⎪⎫－12 12×⎝ ⎛⎭⎪⎫－12＋12×1212×12＋12×⎝ ⎛⎭⎪⎫－12 12×⎝ ⎛⎭⎪⎫－12＋12×12＝⎣⎢⎡⎦⎥⎤0 00 0.答案 ⎣⎢⎡⎦⎥⎤0 00 0 3．设A ＝⎣⎢⎡⎦⎥⎤－1 0 0 1，B ＝⎣⎢⎡⎦⎥⎤0 －11 0，则AB 的逆矩阵为________． 解析 ∵A－1＝⎣⎢⎡⎦⎥⎤－1 0 0 1，B －1＝⎣⎢⎡⎦⎥⎤0 1－1 0 ∴(AB )－1＝B －1A －1＝⎣⎢⎡⎦⎥⎤ 0 1－1 0 ⎣⎢⎡⎦⎥⎤－1 0 0 1＝⎣⎢⎡⎦⎥⎤0 11 0. 答案 ⎣⎢⎡⎦⎥⎤0 11 0 4．函数y ＝x 2在矩阵M ＝⎣⎢⎢⎡⎦⎥⎥⎤10014变换作用下的结果为________． 解析 ⎣⎢⎢⎡⎦⎥⎥⎤1 00 14 ⎣⎢⎡⎦⎥⎤x y ＝⎣⎢⎢⎡⎦⎥⎥⎤ x 14y ＝⎣⎢⎡⎦⎥⎤x ′y ′⇒x ＝x ′，y ＝4y ′， 代入y ＝x 2，得y ′＝14x ′2，即y ＝14x 2. 答案 y ＝14x 25．若A ＝⎣⎢⎡⎦⎥⎤1 56 2，则A 的特征值为________． 解析 A 的特征多项式f (λ)＝⎪⎪⎪⎪⎪⎪⎪⎪λ－1 －5 －6 λ－2 ＝(λ－1)(λ－2)－30＝λ2－3λ－28＝(λ－7)(λ＋4)， ∴A 的特征值为λ1＝7，λ2＝－4. 答案 7和－4考点一 矩阵与变换【例1】 (2014·苏州市自主学习调查)已知a ，b 是实数，如果矩阵M ＝⎣⎢⎡⎦⎥⎤2a b 1所对应的变换将直线x －y ＝1变换成x ＋2y ＝1，求a ，b 的值．解 设点(x ，y )是直线x －y ＝1上任意一点，在矩阵M 的作用下变成点(x ′，y ′)，则⎣⎢⎡⎦⎥⎤2 a b1 ⎣⎢⎡⎦⎥⎤x y ＝⎣⎢⎡⎦⎥⎤x ′y ′， 所以⎩⎨⎧x ′＝2x ＋ay ，y ′＝bx ＋y .因为点(x ′，y ′)，在直线x ＋2y ＝1上，所以 (2＋2b )x ＋(a ＋2)y ＝1，即⎩⎨⎧2＋2b ＝1，a ＋2＝－1，所以⎩⎪⎨⎪⎧a ＝－3，b ＝－12.规律方法 理解变换的意义，掌握矩阵的乘法运算法则是求解的关键，利用待定系数法，构建方程是解决此类题的关键．【训练1】 已知变换S 把平面上的点A (3,0)，B (2,1)分别变换为点A ′(0,3)，B ′(1，－1)，试求变换S 对应的矩阵T . 解 设T ＝⎣⎢⎡⎦⎥⎤a c bd ，则T ：⎣⎢⎡⎦⎥⎤30→⎣⎢⎡⎦⎥⎤x ′y ′＝⎣⎢⎡⎦⎥⎤a c b d ⎣⎢⎡⎦⎥⎤30＝⎣⎢⎡⎦⎥⎤3a 3b ＝⎣⎢⎡⎦⎥⎤03，解得⎩⎨⎧a ＝0，b ＝1；T ：⎣⎢⎡⎦⎥⎤21→⎣⎢⎡⎦⎥⎤x ′y ′＝⎣⎢⎡⎦⎥⎤a c b d ⎣⎢⎡⎦⎥⎤21＝⎣⎢⎡⎦⎥⎤2a ＋c 2b ＋d ＝⎣⎢⎡⎦⎥⎤ 1－1， 解得⎩⎨⎧c ＝1，d ＝－3，综上可知T ＝⎣⎢⎡⎦⎥⎤0 11 －3. 考点二 二阶逆矩阵与二元一次方程组【例2】 已知矩阵M ＝⎣⎢⎡⎦⎥⎤2 －31 －1所对应的线性变换把点A (x ，y )变成点A ′(13,5)，试求M 的逆矩阵及点A 的坐标．解 依题意得由M ＝⎣⎢⎡⎦⎥⎤2 －31 －1，得|M |＝1， 故M －1＝⎣⎢⎡⎦⎥⎤－13－12. 从而由⎣⎢⎡⎦⎥⎤2 －31 －1⎣⎢⎡⎦⎥⎤x y ＝⎣⎢⎢⎡⎦⎥⎥⎤135得⎣⎢⎡⎦⎥⎤x y ＝⎣⎢⎢⎡⎦⎥⎥⎤－1－1 32⎣⎢⎢⎡⎦⎥⎥⎤135＝⎣⎢⎡⎦⎥⎤－1×13＋3×5－1×13＋2×5＝⎣⎢⎡⎦⎥⎤ 2－3，故⎩⎨⎧x ＝2，y ＝－3，∴A (2，－3)为所求． 规律方法 求逆矩阵时，可用定义法解方程处理，也可以用公式法直接代入求解．在求逆矩阵时要重视(AB )－1＝B －1A －1性质的应用． 【训练2】 已知矩阵A ＝⎣⎢⎢⎡⎦⎥⎥⎤21 32， (1)求矩阵A 的逆矩阵；(2)利用逆矩阵知识解方程组⎩⎨⎧2x ＋3y －1＝0，x ＋2y －3＝0.解 (1)法一 设逆矩阵为A －1＝⎣⎢⎢⎡⎦⎥⎥⎤a c b d ， 则由⎣⎢⎢⎡⎦⎥⎥⎤2132⎣⎢⎢⎡⎦⎥⎥⎤a cb d ＝⎣⎢⎢⎡⎦⎥⎥⎤1001，得⎩⎨⎧2a ＋3c ＝1，2b ＋3d ＝0，a ＋2c ＝0，b ＋2d ＝1，解得⎩⎨⎧a ＝2，b ＝－3，c ＝－1，d ＝2，A －1＝⎣⎢⎢⎡⎦⎥⎥⎤2－1－32. 法二 由公式知若A ＝⎣⎢⎢⎡⎦⎥⎥⎤a c b d ＝⎣⎢⎢⎡⎦⎥⎥⎤2132，(2)已知方程组⎩⎨⎧2x ＋3y －1＝0，x ＋2y －3＝0，可转化为⎩⎨⎧2x ＋3y ＝1，x ＋2y ＝3，即AX ＝B ，其中A ＝⎣⎢⎢⎡⎦⎥⎥⎤21 32，X ＝⎣⎢⎢⎡⎦⎥⎥⎤x y ，B ＝⎣⎢⎢⎡⎦⎥⎥⎤13，且由(1)， 得A －1＝⎣⎢⎢⎡⎦⎥⎥⎤2－1 －32. 因此，由AX ＝B ，同时左乘A －1，有 A －1AX ＝A －1B ＝⎣⎢⎢⎡⎦⎥⎥⎤2－1 －32⎣⎢⎢⎡⎦⎥⎥⎤13＝⎣⎢⎢⎡⎦⎥⎥⎤－75. 即原方程组的解为⎩⎨⎧x ＝－7，y ＝5.考点三 求矩阵的特征值与特征向量【例3】 已知a ∈R ，矩阵A ＝⎣⎢⎢⎡⎦⎥⎥⎤1a21对应的线性变换把点P (1,1)变成点P ′(3,3)，求矩阵A 的特征值以及每个特征值的一个特征向量． 解 由题意⎣⎢⎢⎡⎦⎥⎥⎤1a21 ⎣⎢⎢⎡⎦⎥⎥⎤11＝⎣⎢⎢⎡⎦⎥⎥⎤3a ＋1＝⎣⎢⎢⎡⎦⎥⎥⎤33， 得a ＋1＝3，即a ＝2，矩阵A 的特征多项式为 f (λ)＝⎪⎪⎪⎪⎪⎪⎪⎪λ－1－2 －2λ－1＝(λ－1)2－4＝(λ＋1)(λ－3)， 令f (λ)＝0，所以矩阵A 的特征值为λ1＝－1，λ2＝3. ①对于特征值λ1＝－1，解相应的线性方程组⎩⎨⎧ x ＋y ＝0，2x ＋2y ＝0得一个非零解⎩⎨⎧x ＝1，y ＝－1.因此，α＝⎣⎢⎢⎡⎦⎥⎥⎤1－1是矩阵A 的属于特征值λ1＝－1的一个特征向量； ②对于特征值λ2＝3，解相应的线性方程组⎩⎨⎧2x －2y ＝0，－2x ＋2y ＝0得一个非零解⎩⎨⎧x ＝1，y ＝1.因此，β＝⎣⎢⎢⎡⎦⎥⎥⎤11是矩阵A 的属于特征值λ2＝3的一个特征向量． 规律方法 已知A ＝⎣⎢⎢⎡⎦⎥⎥⎤a cb d ，求特征值和特征向量，其步骤为： (1)令f (λ)＝⎪⎪⎪⎪⎪⎪(λ－a )－c －b(λ－d )＝(λ－a )(λ－d )－bc ＝0，求出特征值λ； (2)列方程组⎩⎪⎨⎪⎧(λ－a )x －by ＝0，－cx ＋(λ－d )y ＝0；(3)赋值法求特征向量，一般取x ＝1或者y ＝1，写出相应的向量．【训练3】 (2014·扬州质检)已知矩阵M ＝⎣⎢⎢⎡⎦⎥⎥⎤3－1－13，求M 的特征值及属于各特征值的一个特征向量．解 由矩阵M 的特征多项式f (λ)＝⎪⎪⎪⎪⎪⎪⎪⎪λ－311λ－3＝ (λ－3)2－1＝0，解得λ1＝2，λ2＝4，即为矩阵M 的特征值． 设矩阵M 的特征向量为⎣⎢⎡⎦⎥⎤x y ，当λ1＝2时，由M ⎣⎢⎡⎦⎥⎤x y ＝2⎣⎢⎡⎦⎥⎤x y ，可得⎩⎨⎧－x ＋y ＝0，x －y ＝0.可令x ＝1，得y ＝1，∴α1＝⎣⎢⎡⎦⎥⎤11是M 的属于λ1＝2的特征向量．当λ2＝4时，由M ⎣⎢⎡⎦⎥⎤x y ＝4⎣⎢⎡⎦⎥⎤x y ，可得⎩⎨⎧x ＋y ＝0，x ＋y ＝0，取x ＝1，得y ＝－1，∴α2＝⎣⎢⎡⎦⎥⎤1－1是M 的属于λ2＝4的特征向量．用坐标转移的思想求曲线在变换作用下的新方程【典例】 二阶矩阵M 对应的变换T 将点(1，－1)与(－2，1)分别变换成点(－1，－1)与(0，－2)． (1)求矩阵M ；(2)设直线l 在变换T 作用下得到了直线m ：x －y ＝4，求l 的方程．[审题视点] (1)变换前后的坐标均已知，因此可以设出矩阵，用待定系数法求解． (2)知道直线l 在变换T 作用下的直线m ，求原直线，可用坐标转移法． 解 (1)设M ＝⎣⎢⎡⎦⎥⎤a b c d ，则⎣⎢⎡⎦⎥⎤a b c d ⎣⎢⎡⎦⎥⎤ 1－1＝⎣⎢⎢⎡⎦⎥⎥⎤－1－1， ⎣⎢⎡⎦⎥⎤a b c d ⎣⎢⎡⎦⎥⎤－2 1＝⎣⎢⎡⎦⎥⎤ 0－2， 所以⎩⎪⎨⎪⎧ a －b ＝－1，c －d ＝－1，且⎩⎪⎨⎪⎧－2a ＋b ＝0，－2c ＋d ＝－2，解得⎩⎪⎨⎪⎧a ＝1，b ＝2，c ＝3，d ＝4，所以M ＝⎣⎢⎡⎦⎥⎤1 23 4. (2)因为⎣⎢⎡⎦⎥⎤x ′y ′＝⎣⎢⎡⎦⎥⎤1 23 4⎣⎢⎡⎦⎥⎤x y ＝⎣⎢⎢⎡⎦⎥⎥⎤x ＋2y 3x ＋4y 且m ：x ′－y ′＝4， 所以(x ＋2y )－(3x ＋4y )＝4，即x ＋y ＋2＝0，∴直线l 的方程是x ＋y ＋2＝0.[反思感悟] (1)本题考查了求变换矩阵和在变换矩阵作用下的曲线方程问题，题目难度属中档题．(2)本题突出体现了待定系数法的思想方法和坐标转移的思想方法 .(3)本题的易错点是计算错误和第(2)问中坐标转移的方向错误． 【自主体验】(2014·南京金陵中学月考)求曲线2x 2－2xy ＋1＝0在矩阵MN 对应的变换作用下得到的曲线方程，其中M ＝⎣⎢⎢⎡⎦⎥⎥⎤10 02，N ＝⎣⎢⎢⎡⎦⎥⎥⎤ 1－101. 解 MN ＝⎣⎢⎢⎡⎦⎥⎥⎤1002⎣⎢⎢⎡⎦⎥⎥⎤ 1－101＝⎣⎢⎢⎡⎦⎥⎥⎤ 1－202. 设P (x ′，y ′)是曲线2x 2－2xy ＋1＝0上任意一点，点P 在矩阵MN 对应的变换下变为点P ′(x ，y )， 则⎣⎢⎢⎡⎦⎥⎥⎤x y ＝⎣⎢⎢⎡⎦⎥⎥⎤ 1－202⎣⎢⎢⎡⎦⎥⎥⎤x ′y ′＝⎣⎢⎡⎦⎥⎤ x ′－2x ′＋2y ′， 于是x ′＝x ，y ′＝x ＋y2，代入2x ′2－2x ′y ′＋1＝0，得xy ＝1.所以曲线2x 2－2xy ＋1＝0在MN 对应的变换作用下得到的曲线方程为xy ＝1.一、填空题1．已知变换T ：⎣⎢⎡⎦⎥⎤x y →⎣⎢⎡⎦⎥⎤x ′y ′＝⎣⎢⎡⎦⎥⎤3x ＋4y 5x ＋6y ，则该变换矩阵为________． 解析 ⎩⎪⎨⎪⎧x ′＝3x ＋4y ，y ′＝5x ＋6y ，可写成⎣⎢⎡⎦⎥⎤3 45 6⎣⎢⎡⎦⎥⎤x y ＝⎣⎢⎡⎦⎥⎤x ′y ′. 答案 ⎣⎢⎡⎦⎥⎤3 45 6 2．计算⎣⎢⎡⎦⎥⎤3 75 8⎣⎢⎡⎦⎥⎤2－1等于________． 解析 ⎣⎢⎡⎦⎥⎤3 75 8⎣⎢⎡⎦⎥⎤ 2－1＝⎣⎢⎢⎡⎦⎥⎥⎤3×2－75×2－8＝⎣⎢⎡⎦⎥⎤－1 2. 答案 ⎣⎢⎡⎦⎥⎤－1 23．矩阵⎣⎢⎡⎦⎥⎤5 00 1的逆矩阵为________． 解析 ⎣⎢⎡⎦⎥⎤5 00 1＝5，∴⎣⎢⎡⎦⎥⎤5 00 1的逆矩阵为⎣⎢⎢⎡⎦⎥⎥⎤15 0 0 1. 答案 ⎣⎢⎢⎡⎦⎥⎥⎤15 0 0 1 4．若矩阵A ＝⎣⎢⎡⎦⎥⎤3 a b 13把直线l ：2x ＋y －7＝0变换成另一直线l ′：9x ＋y －91＝0，则a ＝________，b ＝________. 解析 取l 上两点(0,7)和(3.5,0)，则⎣⎢⎡⎦⎥⎤3 a b 13⎣⎢⎡⎦⎥⎤07＝⎣⎢⎡⎦⎥⎤7a 91，⎣⎢⎡⎦⎥⎤3 a b 13⎣⎢⎡⎦⎥⎤3.5 0＝⎣⎢⎡⎦⎥⎤10.53.5b . 由已知(7a,91)，(10.5,3.5b )在l ′上，代入得a ＝0，b ＝－1. 答案 0 －15．矩阵M ＝⎣⎢⎡⎦⎥⎤6 －36 －3的特征值为________． 解析 f (λ)＝⎪⎪⎪⎪⎪⎪⎪⎪λ－6 3－6 λ＋3＝(λ－6)(λ＋3)＋18＝0. ∴λ＝0或λ＝3. 答案 0或3 6．已知矩阵M ＝⎣⎢⎡⎦⎥⎤1234，α＝⎣⎢⎡⎦⎥⎤12，β＝⎣⎢⎡⎦⎥⎤ 0－3，则M (2α＋4β)＝________.解析 2α＋4β＝⎣⎢⎡⎦⎥⎤24＋⎣⎢⎡⎦⎥⎤ 0－12＝⎣⎢⎡⎦⎥⎤ 2－8，M (2α＋4β)＝⎣⎢⎡⎦⎥⎤1 23 4⎣⎢⎡⎦⎥⎤ 2－8＝⎣⎢⎢⎡⎦⎥⎥⎤－14－26.答案 ⎣⎢⎡⎦⎥⎤－14－26 7．曲线C 1：x 2＋2y 2＝1在矩阵M ＝⎣⎢⎢⎡⎦⎥⎥⎤121的作用下变换为曲线C 2，则C 2的方程为________．解析 设P (x ，y )为曲线C 2上任意一点，P ′(x ′，y ′)为曲线x 2＋2y 2＝1上与P 对应的点，则⎣⎢⎢⎡⎦⎥⎥⎤10 21⎣⎢⎢⎡⎦⎥⎥⎤x ′ y ′＝⎣⎢⎢⎡⎦⎥⎥⎤x y ，即⎩⎪⎨⎪⎧ x ＝x ′＋2y ′，y ＝y ′⇒⎩⎪⎨⎪⎧x ′＝x －2y ，y ′＝y . 因为P ′是曲线C 1上的点， 所以C 2的方程为(x －2y )2＋y 2＝1. 答案 (x －2y )2＋y 2＝18．已知矩阵A ＝⎣⎢⎡⎦⎥⎤2 －1－4 3，B ＝⎣⎢⎡⎦⎥⎤4 －1－3 1，则满足AX ＝B 的二阶矩阵X 为________．解析 由题意，得A －1＝ AX ＝B ， ∴X ＝A －1B ＝. 答案 ⎣⎢⎢⎡⎦⎥⎥⎤92 －1 5 －1 9．已知矩阵A 将点(1,0)变换为(2,3)，且属于特征值3的一个特征向量是⎣⎢⎢⎡⎦⎥⎥⎤11，则矩阵A 为________．解析 设A ＝⎣⎢⎢⎡⎦⎥⎥⎤a c b d ，由⎣⎢⎢⎡⎦⎥⎥⎤a c b d ⎣⎢⎢⎡⎦⎥⎥⎤10＝⎣⎢⎢⎡⎦⎥⎥⎤23，得⎩⎪⎨⎪⎧a ＝2，c ＝3. 由⎣⎢⎢⎡⎦⎥⎥⎤a cb d ⎣⎢⎢⎡⎦⎥⎥⎤11＝3⎣⎢⎢⎡⎦⎥⎥⎤11＝⎣⎢⎢⎡⎦⎥⎥⎤33，得⎩⎪⎨⎪⎧ a ＋b ＝3，c ＋d ＝3.所以⎩⎪⎨⎪⎧b ＝1，d ＝0.所以A ＝⎣⎢⎢⎡⎦⎥⎥⎤23 10.答案 ⎣⎢⎢⎡⎦⎥⎥⎤23 10 二、解答题10．(2012·江苏卷)已知矩阵A 的逆矩阵A －1＝错误!，求矩阵A 的特征值． 解 因为AA －1＝E ，所以A ＝(A －1)－1.因为A －1＝错误!，所以A ＝(A －1)－1＝错误!， 于是矩阵A 的特征多项式为 f (λ)＝⎪⎪⎪⎪⎪⎪⎪⎪λ－2－2 －3λ－1＝λ2－3λ－4. 令f (λ)＝0，解得A 的特征值λ1＝－1，λ2＝4. 11．已知矩阵A ＝⎣⎢⎡⎦⎥⎤ 1a －1b ，A 的一个特征值λ＝2，其对应的特征向量是α1＝⎣⎢⎡⎦⎥⎤21.(1)求矩阵A ；(2)若向量β＝⎣⎢⎡⎦⎥⎤74，计算A 5β的值．解 (1)A ＝⎣⎢⎡⎦⎥⎤1 2－1 4. (2)矩阵A 的特征多项式为f (λ)＝⎪⎪⎪⎪⎪⎪λ－1 －2 1 λ－4＝λ2－5λ＋6＝0，得λ1＝2，λ2＝3，当λ1＝2时，α1＝⎣⎢⎡⎦⎥⎤21，当λ2＝3时，得α2＝⎣⎢⎡⎦⎥⎤11.由β＝m α1＋n α2，得⎩⎨⎧2m ＋n ＝7，m ＋n ＝4，解得m ＝3，n ＝1.∴A 5β＝A 5(3α1＋α2)＝3(A 5α1)＋A5α2＝3(λ51α1)＋λ52α2＝3×25⎣⎢⎡⎦⎥⎤21＋35⎣⎢⎡⎦⎥⎤11＝⎣⎢⎡⎦⎥⎤435339.12．(2012·福建卷)设曲线2x 2＋2xy ＋y 2＝1在矩阵A ＝⎣⎢⎡⎦⎥⎤a0b1(a ＞0)对应的变换作用下得到的曲线为x 2＋y 2＝1. (1)求实数a ，b 的值； (2)求A 2的逆矩阵．解 (1)设曲线2x 2＋2xy ＋y 2＝1上任意点P (x ，y )在矩阵A 对应的变换作用下的像是P ′(x ′，y ′)． 由⎣⎢⎡⎦⎥⎤x ′y ′＝⎣⎢⎡⎦⎥⎤a 0b1⎣⎢⎡⎦⎥⎤x y ＝⎣⎢⎡⎦⎥⎤ ax bx ＋y ，得⎩⎨⎧x ′＝ax ，y ′＝bx ＋y .又点P ′(x ′，y ′)在x 2＋y 2＝1上，所以x ′2＋y ′2＝1， 即a 2x 2＋(bx ＋y )2＝1，整理得(a 2＋b 2)x 2＋2bxy ＋y 2＝1，依题意得⎩⎨⎧ a 2＋b 2＝2，2b ＝2，解得⎩⎨⎧ a ＝1，b ＝1或⎩⎨⎧a ＝－1，b ＝1.因为a ＞0，所以⎩⎨⎧a ＝1，b ＝1.(2)由(1)知，A ＝⎣⎢⎡⎦⎥⎤1011，A 2＝⎣⎢⎡⎦⎥⎤1 01 1⎣⎢⎡⎦⎥⎤1 01 1＝⎣⎢⎡⎦⎥⎤1 02 1. 所以|A 2|＝1，(A 2)－1＝⎣⎢⎡⎦⎥⎤10－21.。

.4。

2二阶矩阵与二元一次方程组一、消元法二求解元一次方程组错误!当ad －bc≠0时，方程组的解为错误!二、二阶行列式定义:det(A ） ＝a b c d ＝ad －bc 因此方程组的解为错误! 记：D ＝a b c d ，D x ＝m b n d，D y ＝a m c n ，所以，方程组的解为错误! 例1 求下列行列式的值⑴ 21 43 ⑵21 43- ⑶21 - 40 ⑷ 2b a dc 解：⑴21 43=1×4—2×3=—2 ⑵21 43-=1×4—2×（—3）=10 ⑶21 - 40=-1×4—2×0=-4 ⑷2b a dc =2（ad —bc) 例2 若x= θθsin con θθcon sin （θ∈R ） 试求f(x)=x 2+2x —3 的最值。

解:∵x= θθsin con θθcon sin =con 2θ-sin 2θ=con2θ ∴-1≤x ≤1 ∵f （x)=x 2+2x —3=(x+1）2-4∴当x=—1时f （x ） 取得最小值 -4； 当x=1时f （x ）取得最大值0例3 利用行列式求解二元一次方程组⎩⎨⎧=+=-7y 3x 42y 3x 例4 利用行列式求解A ＝⎢⎣⎡33 ⎥⎦⎤12-的逆矩阵 应用:一、用逆矩阵方法求二元一次方程组⎩⎨⎧=+=-7y 3x 42y 3x 的解 解：已知方程组可以写为:⎢⎣⎡33 ⎥⎦⎤12-⎥⎦⎤⎢⎣⎡y x =⎥⎦⎤⎢⎣⎡74 令M=⎢⎣⎡33 ⎥⎦⎤12- 其行列式33 12-=3×1-3×（-2）=9≠0∴M -1 =⎢⎢⎢⎣⎡93-91 ⎥⎥⎥⎦⎤9392 = ⎢⎢⎢⎣⎡31-91 ⎥⎥⎥⎦⎤3192 ∴⎥⎦⎤⎢⎣⎡y x = M -1⎥⎦⎤⎢⎣⎡74=⎢⎢⎢⎣⎡31-91 ⎥⎥⎥⎦⎤3192⎥⎦⎤⎢⎣⎡74=⎥⎦⎤⎢⎣⎡12 即方程组的解为：⎩⎨⎧==1y 2x 二、用几何变换的观点讨论方程的解（1）错误!(2）AX ＝B ，其中A ＝11⎡⎢⎣ 00⎤⎥⎦，B ＝22⎡⎤⎢⎥⎣⎦尊敬的读者：本文由我和我的同事在百忙中收集整编出来，本文稿在发布之前我们对内容进行仔细校对，但是难免会有不尽如人意之处，如有疏漏之处请指正，希望本文能为您解开疑惑,引发思考。

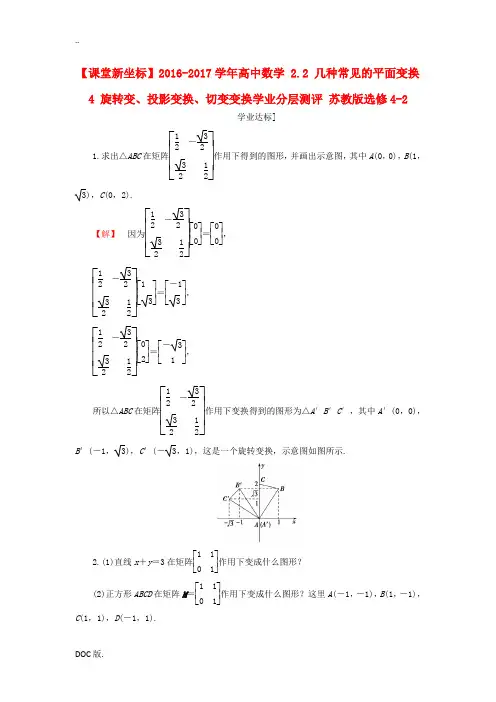
【课堂新坐标】2016-2017学年高中数学 2.2 几种常见的平面变换 4 旋转变、投影变换、切变变换学业分层测评 苏教版选修4-2学业达标]1.求出△ABC 在矩阵⎣⎢⎢⎡⎦⎥⎥⎤12 －3232 12作用下得到的图形，并画出示意图，其中A (0，0)，B (1，3)，C (0，2).【解】 因为⎣⎢⎢⎡⎦⎥⎥⎤12 －3232 12⎣⎢⎡⎦⎥⎤00＝⎣⎢⎡⎦⎥⎤00， ⎣⎢⎢⎡⎦⎥⎥⎤12 －3232 12⎣⎢⎡⎦⎥⎤13＝⎣⎢⎡⎦⎥⎤－13，⎣⎢⎢⎡⎦⎥⎥⎤12 －3232 12⎣⎢⎡⎦⎥⎤02＝⎣⎢⎡⎦⎥⎤－3 1， 所以△ABC 在矩阵⎣⎢⎢⎡⎦⎥⎥⎤12 －3232 12作用下变换得到的图形为△A ′B ′C ′，其中A ′(0，0)，B ′(－1，3)，C ′(－3，1)，这是一个旋转变换，示意图如图所示.2.(1)直线x ＋y ＝3在矩阵⎣⎢⎡⎦⎥⎤1 10 1作用下变成什么图形？ (2)正方形ABCD 在矩阵M ＝⎣⎢⎡⎦⎥⎤1 101作用下变成什么图形？这里A (－1，－1)，B (1，－1)，C (1，1)，D (－1，1).【解】 (1)直线x ＋y ＝3在矩阵⎣⎢⎡⎦⎥⎤1 10 1作用下变成直线x ＝3. (2)在矩阵M ＝⎣⎢⎡⎦⎥⎤1 101对应变换下，A →A ′(－2，－1)，B →B ′(0，－1)，C →C ′(2，1)，D →D ′(0，1)，则变换所成图形为平行四边形A ′B ′C ′D ′，如图.3.椭圆x 29＋y 2＝1在矩阵⎣⎢⎡⎦⎥⎤1000对应的变换作用下得到什么图形？【解】 设(x ，y )为椭圆x 29＋y 2＝1上的任意一点，则有x 2≤9.因为⎣⎢⎡⎦⎥⎤1000⎣⎢⎡⎦⎥⎤x y ＝⎣⎢⎡⎦⎥⎤x 0，所以矩阵⎣⎢⎡⎦⎥⎤1 00 0使得椭圆上的点的横坐标保持不变，纵坐标变为0，所以椭圆x 29＋y 2＝1在矩阵⎣⎢⎡⎦⎥⎤1 000对应的变换作用下得到的图形是线段y ＝0(－3≤x ≤3)，即椭圆长轴.4.在平面直角坐标系xOy 内有一点P (2，3)，将该点沿平行于直线x ＋2y ＝0的方向投影到x 轴上，求P (2，3)在此投影变换下得到的点P ′的坐标.【解】 设P (2，3)在此投影变换下得到的点为P ′(x ′，y ′)，则由题意知⎩⎪⎨⎪⎧x ′＝x ＋2y ，y ′＝0，即⎣⎢⎡⎦⎥⎤x y →⎣⎢⎡⎦⎥⎤x ′y ′＝⎣⎢⎡⎦⎥⎤x ＋2y 0，从而可知此投影变换对应的矩阵为⎣⎢⎡⎦⎥⎤1 20 0，由⎣⎢⎡⎦⎥⎤1 20 0⎣⎢⎡⎦⎥⎤23＝⎣⎢⎡⎦⎥⎤80，可知点P ′的坐标为(8，0). 5.如图2­2­4所示，已知△ABC 在变换T 的作用下变成△A ′B ′C ′，试求变换T 对应的矩阵M .【导学号：30650020】图2­2­4【解】 从△ABC 到△A ′B ′C ′对应的是x 轴方向上的切变变换，因为A 、B 在x 轴上，原地不变，注意到C (－1，1)→C ′(1，1)，由此可知这个变换对应的矩阵为⎣⎢⎡⎦⎥⎤1 201.6.如图2­2­5所示，已知矩形ABCD 在变换T 的作用下变成图形A ′B ′C ′D ′，试求变换T 对应的矩阵M .图2­2­5【解】 从图可以看出，T 是一个切变变换，且T ：⎣⎢⎡⎦⎥⎤x y →⎣⎢⎡⎦⎥⎤x ′y ′＝⎣⎢⎢⎡⎦⎥⎥⎤ x y ＋12x . 故T 对应的变换矩阵为M ＝⎣⎢⎢⎡⎦⎥⎥⎤1 012 1. 我们可以进行如下验证：⎣⎢⎢⎡⎦⎥⎥⎤1 012 1⎣⎢⎡⎦⎥⎤20＝⎣⎢⎡⎦⎥⎤21，⎣⎢⎢⎡⎦⎥⎥⎤1 012 1⎣⎢⎡⎦⎥⎤21＝⎣⎢⎡⎦⎥⎤22，⎣⎢⎢⎡⎦⎥⎥⎤1 012 1⎣⎢⎡⎦⎥⎤－2 1＝⎣⎢⎡⎦⎥⎤－2 0，⎣⎢⎢⎡⎦⎥⎥⎤1 012 1⎣⎢⎡⎦⎥⎤－2 0＝⎣⎢⎡⎦⎥⎤－2－1. 所以矩形ABCD 在矩阵⎣⎢⎢⎡⎦⎥⎥⎤1 012 1的作用下变成了平行四边形A ′B ′C ′D ′. 7.试分析平面上的变换将平面上的点沿垂直于直线y ＝x 的方向投影到直线y ＝x 上的矩阵表示.【解】 不妨设P (x ，y )是平面上的任意一点，则它关于直线y ＝x 对称的点P ′的坐标为P ′(y ，x )，PP ′的连线一定垂直于直线y ＝x ，且交点为Q ⎝ ⎛⎭⎪⎫x ＋y 2，x ＋y 2，如图所示.根据题意，该变换即为⎣⎢⎡⎦⎥⎤x y →⎣⎢⎡⎦⎥⎤x ′y ′＝⎣⎢⎢⎡⎦⎥⎥⎤x ＋y 2x ＋y 2＝⎣⎢⎢⎡⎦⎥⎥⎤12 1212 12⎣⎢⎡⎦⎥⎤x y .因此，将平面上的点沿垂直于直线y ＝x 的方向投影到直线y ＝x 上的变换的矩阵表示为⎣⎢⎢⎡⎦⎥⎥⎤12 1212 12. 能力提升]8.运用旋转矩阵对应变换，求解下列问题：(1)求曲线x ＝y 2逆时针方向绕原点旋转90°所成的曲线方程. (2)求圆x 2＋y 2＝1绕原点逆时针旋转π8后得到的曲线方程.【导学号：30650021】【解】 (1)旋转变换矩阵为：⎣⎢⎡⎦⎥⎤cos 90° －sin 90°sin 90° cos 90°＝⎣⎢⎡⎦⎥⎤0 －11 0，设x ＝y 2上任意一点(x 0，y 0)旋转变换后为(x ′0，y ′0)，则⎣⎢⎡⎦⎥⎤x ′0y ′0＝⎣⎢⎡⎦⎥⎤0 －11 0⎣⎢⎡⎦⎥⎤x 0y 0＝⎣⎢⎡⎦⎥⎤－y 0 x 0， 所以⎩⎪⎨⎪⎧x ′0＝－y 0y ′0＝x 0，故y ′0＝(－x ′0)2，即旋转所成的曲线方程为y ＝x 2.(2)设x 2＋y 2＝1上的动点P (x ，y )经过变换后得新曲线上的点为P ′(x ′，y ′). 则有⎣⎢⎡⎦⎥⎤x ′y ′＝⎣⎢⎢⎡⎦⎥⎥⎤cos π8 －sin π8sin π8 cos π8⎣⎢⎡⎦⎥⎤x y＝⎣⎢⎢⎡⎦⎥⎥⎤x cos π8－y sin π8x sin π8＋y cos π8， 故⎩⎪⎨⎪⎧x ′＝x cos π8－y sin π8，y ′＝x sin π8＋y cos π8.从而⎩⎪⎨⎪⎧x ＝x ′cos π8＋y ′sin π8，y ＝－x ′sin π8＋y ′cos π8.代入x 2＋y 2＝1得(x ′cos π8＋y ′sin π8)2＋(－x ′sin π8＋y ′cos π8)2＝1，即x ′2＋y ′2＝1.故所求曲线方程为x 2＋y 2＝1.。

2．4.1 逆矩阵的概念1．逆矩阵的定义对于二阶矩阵A 、B ，假设有AB ＝BA ＝E ，那么称A 是可逆的，B 称为A 的逆矩阵，记为A －1.2．逆矩阵的性质(1)假设二阶矩阵A 、B 均可逆，那么AB 也可逆，且(AB )－1＝B －1A －1. (2)A 、B 、C 为二阶矩阵且AB ＝AC ，假设A 存在逆矩阵，那么B ＝C . 3．逆矩阵的求法(1)公式法：对于二阶矩阵A ＝⎣⎢⎡⎦⎥⎤ab cd ，假设ad －bc ≠0，那么A 必可逆，且A －1＝⎣⎢⎢⎡⎦⎥⎥⎤d ad －bc －bad －bc －c ad －bc a ad －bc .(2)待定系数法． (3)逆变换法．[对应学生用书P30]逆矩阵的求法[例1] 求矩阵A ＝⎣⎡⎦⎤3 22 1的逆矩阵．[思路点拨] 设出逆矩阵，利用待定系数法求解或直接利用公式法求解．[精解详析] 法一：待定系数法：设A －1＝⎣⎢⎡⎦⎥⎤xy zw ，那么⎣⎢⎡⎦⎥⎤3 221⎣⎢⎡⎦⎥⎤xy zw ＝⎣⎢⎡⎦⎥⎤1001.即⎣⎡⎦⎤3x ＋2z 3y ＋2w 2x ＋z 2y ＋w ＝⎣⎡⎦⎤1 00 1，故⎩⎪⎨⎪⎧3x ＋2z ＝1，2x ＋z ＝0，⎩⎪⎨⎪⎧3y ＋2w ＝0，2y ＋w ＝1，解得x ＝－1，z ＝2，y ＝2，w ＝－3， 从而A 的逆矩阵为A －1＝⎣⎡⎦⎤－122－3.法二：公式法：ad －bc ＝3×1－2×2＝－1≠0，∴A －1＝⎣⎢⎡⎦⎥⎤－122－3.用待定系数法求逆矩阵时，先设出矩阵A 的逆矩阵A －1，再由AA －1＝E 得相等矩阵，最后利用相等矩阵的概念求出A －1.1．(某某高考)矩阵A ＝⎣⎢⎡⎦⎥⎤－1002，B ＝⎣⎢⎡⎦⎥⎤1206，求矩阵A －1B .解：设矩阵A 的逆矩阵为⎣⎢⎡⎦⎥⎤ab cd ，那么⎣⎢⎡⎦⎥⎤－10 02⎣⎢⎡⎦⎥⎤ab cd ＝⎣⎢⎡⎦⎥⎤1001，即⎣⎢⎡⎦⎥⎤－a －b 2c 2d ＝⎣⎢⎡⎦⎥⎤1 001故a ＝－1，b ＝0，c ＝0，d ＝12，从而A 的逆矩阵为A －1＝⎣⎢⎢⎡⎦⎥⎥⎤－1 0 0 12，所以A －1B ＝⎣⎢⎢⎡⎦⎥⎥⎤－10 0 12⎣⎢⎡⎦⎥⎤1 20 6＝⎣⎢⎡⎦⎥⎤－1 －2 0 3. 2．矩阵M ＝⎣⎡⎦⎤21 －3－1所对应的线性变换把点A (x ，y )变成点A ′(13,5)，试求M 的逆矩阵及点A 的坐标．解：由M ＝⎣⎡⎦⎤21 －3－1，得2×(－1)－(－3)×1＝1≠0，故M－1＝⎣⎡⎦⎤－1－1 32.从而由⎣⎡⎦⎤21 －3－1⎣⎡⎦⎤x y ＝⎣⎡⎦⎤135得⎣⎡⎦⎤x y ＝⎣⎡⎦⎤－1－1 32⎣⎡⎦⎤13 5＝⎣⎡⎦⎤－1×13＋3×5－1×13＋2×5＝⎣⎡⎦⎤ 2－3， 故⎩⎪⎨⎪⎧x ＝2，y ＝－3，即A (2，－3)为所求．[例2] 用几何变换的观点求以下矩阵的逆矩阵．(1)A ＝⎣⎢⎡⎦⎥⎤2001；(2)B ＝⎣⎢⎡⎦⎥⎤01－10.[思路点拨] A 为伸压变换矩阵，B 为旋转变换矩阵，只需找到它们的逆变换，再写出逆变换对应的矩阵即为所求．[精解详析](1)矩阵A 为伸压变换矩阵，它对应的几何变换为平面内点的纵坐标保持不变，横坐标沿x 轴方向拉伸为原来2倍的伸缩变换，因此它存在逆变换T A －1：将平面内点的纵坐标保持不变，横坐标沿x 轴方向压缩为原来的12，所对应的变换矩阵为A －1＝⎣⎢⎢⎡⎦⎥⎥⎤12 00 1.(2)矩阵B 为旋转变换矩阵，它对应的几何变换为将平面内的点绕原点顺时针旋转90°.它存在逆变换T B －1：将平面内的点绕原点逆时针旋转90°，所对应的变换矩阵为B －1＝⎣⎢⎡⎦⎥⎤0 －11 0.从几何角度考虑矩阵对应的变换是否存在逆变换，就是观察在变换下是否能“走过去又能走回来〞，即对应的变换是一一映射．关键是熟练掌握反射变换、伸缩变换、旋转变换、切变变换等常用变换对应的矩阵，根据矩阵对应的几何变换找出其逆变换，再写出逆变换对应的矩阵，即为所求逆矩阵．3．矩阵A ＝⎣⎢⎢⎡⎦⎥⎥⎤－1232－32 －12，求A －1.解：矩阵A 对应的变换是旋转变换R 240°，它的逆变换是R －240°∴A －1＝⎣⎢⎡⎦⎥⎤cos －240° －sin －240°sin －240° cos －240°＝⎣⎢⎢⎡⎦⎥⎥⎤－12 －32 32 －12. 4．矩阵A ＝⎣⎢⎢⎡⎦⎥⎥⎤12 0 0 5，求A －1. 解：因矩阵A 所对应的变换为伸缩变换，所以A －1＝⎣⎢⎢⎡⎦⎥⎥⎤2 00 15.逆矩阵的概念与性质的应用[例3] 假设矩阵A ＝⎣⎢⎡⎦⎥⎤2 005，B ＝⎣⎢⎡⎦⎥⎤1 301，求矩阵AB 的逆矩阵．[思路点拨] 根据公式(AB )－1＝B －1A －1，先求出B －1、A －1，再利用矩阵乘法求解． [精解详析] 因为矩阵A 所对应的变换为伸缩变换，所以A－1＝⎣⎢⎢⎡⎦⎥⎥⎤120015. 而矩阵B 对应的变换为切变变换，其逆矩阵B －1＝⎣⎢⎡⎦⎥⎤1 －30 1，∴(AB )－1＝B －1A －1＝⎣⎢⎡⎦⎥⎤1－301⎣⎢⎢⎡⎦⎥⎥⎤120015＝⎣⎢⎢⎡⎦⎥⎥⎤12－350 15.(1)要避免犯如下错误(AB )－1＝A －1B －1. (2)此题也可以先求出AB 再求其逆．5．A ＝⎣⎢⎡⎦⎥⎤1 －10 1⎣⎢⎢⎡⎦⎥⎥⎤12－323212，求A －1.解：设M ＝⎣⎢⎡⎦⎥⎤1 －10 1，N ＝⎣⎢⎢⎡⎦⎥⎥⎤12 －3232 12，那么A ＝MN . ∵1×1－0×(－1)＝1≠0，∴M －1＝⎣⎢⎡⎦⎥⎤1101，同理N －1＝⎣⎢⎢⎡⎦⎥⎥⎤ 1232－32 12.由逆矩阵的性质，得A －1＝(MN )－1＝N －1M －1＝⎣⎢⎢⎡⎦⎥⎥⎤1232－3212⎣⎢⎡⎦⎥⎤1101＝⎣⎢⎢⎡⎦⎥⎥⎤121＋32－321－32. 6．假设矩阵A ＝⎣⎢⎡⎦⎥⎤1001，B ＝⎣⎢⎡⎦⎥⎤1201，求曲线x 2＋y 2＝1在矩阵(AB )－1变换下的曲线方程．解：(AB )－1＝B －1A －1＝⎣⎢⎡⎦⎥⎤1－201⎣⎢⎡⎦⎥⎤1001＝⎣⎢⎡⎦⎥⎤1－201.设P (x ，y )是圆x 2＋y 2＝1上任意一点，P 点在(AB )－1对应变换下变成Q (x ′，y ′) 那么⎣⎢⎡⎦⎥⎤x ′y ′＝⎣⎢⎡⎦⎥⎤1 －20 1⎣⎢⎡⎦⎥⎤x y ＝⎣⎢⎡⎦⎥⎤x －2y y . ∴⎩⎪⎨⎪⎧x ′＝x －2y ，y ′＝y .故⎩⎪⎨⎪⎧x ＝x ′＋2y ′，y ＝y .′∴P (x ′＋2y ′，y ′)．又P 点在圆上，∴(x ′＋2y ′)2＋(y ′)2＝1. 展开整理为(x ′)2＋4x ′y ′＋5(y ′)2＝1. 故所求曲线方程为x 2＋4xy ＋5y 2＝1.[例4] 矩阵A ＝⎣⎢⎡⎦⎥⎤12－2－3，B ＝⎣⎢⎡⎦⎥⎤2312，C ＝⎣⎢⎡⎦⎥⎤0110，求满足AXB ＝C 的矩阵X .[思路点拨] 由AXB ＝C 得X ＝A －1CB －1，从而求解． [精解详析] ∵A －1＝⎣⎢⎡⎦⎥⎤－3 －2 2 1，B －1＝⎣⎢⎡⎦⎥⎤ 2 －3－1 2，∴X ＝A －1CB －1＝⎣⎢⎡⎦⎥⎤－3 －2 2 1⎣⎢⎡⎦⎥⎤0110⎣⎢⎡⎦⎥⎤ 2 －3－1 2 ＝⎣⎢⎡⎦⎥⎤－2 －3 1 2⎣⎢⎡⎦⎥⎤ 2 －3－1 2＝⎣⎢⎡⎦⎥⎤－1 0 01.此种题型要特别注意左乘还是右乘相应的逆矩阵，假设位置错误，那么得不到正确结果，原因是矩阵乘法并不满足交换律．7．矩阵A ＝⎣⎢⎡⎦⎥⎤1 －23 －7.假设矩阵X 满足AX ＝⎣⎢⎡⎦⎥⎤31，试求矩阵X .解：设A －1＝⎣⎢⎡⎦⎥⎤xy zw ，那么⎣⎢⎡⎦⎥⎤1 －23 －7⎣⎢⎡⎦⎥⎤xy zw ＝⎣⎢⎡⎦⎥⎤1 001，即⎣⎢⎡⎦⎥⎤x －2zy －2w 3x －7z 3y －7w ＝⎣⎢⎡⎦⎥⎤1001，所以⎩⎪⎨⎪⎧x －2z ＝1，y －2w ＝0，3x －7z ＝0，3y －7w ＝1，解得⎩⎪⎨⎪⎧x ＝7，y ＝－2，z ＝3，w ＝－1.故所求的逆矩阵A －1＝⎣⎢⎡⎦⎥⎤7 －23 －1.因为AX ＝⎣⎢⎡⎦⎥⎤31，所以A －1AX ＝A －1⎣⎢⎡⎦⎥⎤31， 所以X ＝A －1⎣⎢⎡⎦⎥⎤31＝⎣⎢⎡⎦⎥⎤7 －23 －1⎣⎢⎡⎦⎥⎤31＝⎣⎢⎡⎦⎥⎤19 8. 8．假设点A (2,2)在矩阵M ＝⎣⎢⎡⎦⎥⎤cos α －sin αsin α cos α对应变换的作用下得到的点为B (－2,2)，求矩阵M 的逆矩阵．解：因为M ⎣⎢⎡⎦⎥⎤22＝⎣⎢⎡⎦⎥⎤－2 2，即⎣⎢⎡⎦⎥⎤2cos α－2sin α2sin α＋2cos α＝⎣⎢⎡⎦⎥⎤－2 2，所以⎩⎪⎨⎪⎧cos α－sin α＝－1，sin α＋cos α＝1.解得⎩⎪⎨⎪⎧cos α＝0，sin α＝1.所以M ＝⎣⎢⎡⎦⎥⎤0－110.法一：由M ＝⎣⎢⎡⎦⎥⎤0－110＝⎣⎢⎡⎦⎥⎤cos 90°－sin 90°sin 90°cos 90°，知M 是绕原点O 逆时针旋转90°的旋转变换矩阵，于是M －1＝⎣⎢⎡⎦⎥⎤cos －90°－sin －90°sin －90°cos －90°＝⎣⎢⎡⎦⎥⎤01－10.法二：由M ＝⎣⎢⎡⎦⎥⎤0－110，那么ad －bc ＝1≠0.∴M －1＝⎣⎢⎡⎦⎥⎤01－10.[对应学生用书P32]1．求以下矩阵的逆矩阵．(1)A ＝⎣⎢⎡⎦⎥⎤1123；(2)B ＝⎣⎢⎡⎦⎥⎤2345.解：法一：利用逆矩阵公式．(1)注意到1×3－2×1＝1≠0，故A 存在逆矩阵A －1，且 A －1＝⎣⎢⎢⎡⎦⎥⎥⎤31－11－2111＝⎣⎢⎡⎦⎥⎤3－1－21. (2)注意到2×5－4×3＝－2≠0，故B 存在逆矩阵B －1，且 B －1＝⎣⎢⎢⎡⎦⎥⎥⎤5－2 －3－2－4－2 2－2＝⎣⎢⎢⎡⎦⎥⎥⎤－52 32 2 －1.法二：利用待定系数法． (1)设矩阵A 的逆矩阵为⎣⎢⎡⎦⎥⎤ab cd ，那么⎣⎢⎡⎦⎥⎤1 123⎣⎢⎡⎦⎥⎤ab cd ＝⎣⎢⎡⎦⎥⎤1 001，即⎣⎢⎡⎦⎥⎤a ＋cb ＋d 2a ＋3c 2b ＋3d ＝⎣⎢⎡⎦⎥⎤1 001.故⎩⎪⎨⎪⎧a ＋c ＝1，2a ＋3c ＝0，b ＋d ＝0，2b ＋3d ＝1.解得a ＝3，c ＝－2，b ＝－1，d ＝1. 从而A －1＝⎣⎢⎡⎦⎥⎤3 －1－2 1.(2)设矩阵B 的逆矩阵为⎣⎢⎡⎦⎥⎤xy zw ，那么⎣⎢⎡⎦⎥⎤2 345⎣⎢⎡⎦⎥⎤xy zw ＝⎣⎢⎡⎦⎥⎤1001，即⎣⎢⎡⎦⎥⎤2x ＋3z 2y ＋3w 4x ＋5z 4y ＋5w ＝⎣⎢⎡⎦⎥⎤1 001.故⎩⎪⎨⎪⎧2x ＋3z ＝1，4x ＋5z ＝0，2y ＋3w ＝0，4y ＋5w ＝1.解得x ＝－52，z ＝2，y ＝32，w ＝－1.从而B －1＝⎣⎢⎢⎡⎦⎥⎥⎤－52 322 －1.2．可逆矩阵A ＝⎣⎢⎡⎦⎥⎤a273的逆矩阵A －1＝⎣⎢⎡⎦⎥⎤b －2－7 a ，求a ，b 的值． 解：根据题意，得AA －1＝E ， 所以⎣⎢⎡⎦⎥⎤a27 3⎣⎢⎡⎦⎥⎤ b －2－7 a ＝⎣⎢⎡⎦⎥⎤1 001，即⎣⎢⎡⎦⎥⎤ab －2×7 －2a ＋2a 7b －21 －2×7＋3a ＝⎣⎢⎡⎦⎥⎤1001， 所以⎩⎪⎨⎪⎧ab －14＝1，7b －21＝0，－14＋3a ＝1，解得a ＝5，b ＝3.3．A ＝⎣⎢⎡⎦⎥⎤1 11 2，B ＝⎣⎢⎡⎦⎥⎤2 －1－1 1，求证B 是A 的逆矩阵． 证明：因为A ＝⎣⎢⎡⎦⎥⎤1112，B ＝⎣⎢⎡⎦⎥⎤ 2 －1－1 1， 所以AB ＝⎣⎢⎡⎦⎥⎤111 2⎣⎢⎡⎦⎥⎤ 2 －1－1 1＝⎣⎢⎡⎦⎥⎤1 001，BA ＝⎣⎢⎡⎦⎥⎤ 2 －1－1 1⎣⎢⎡⎦⎥⎤1112＝⎣⎢⎡⎦⎥⎤1 001， 所以B 是A 的逆矩阵．4．求矩阵乘积AB 的逆矩阵． (1)A ＝⎣⎢⎡⎦⎥⎤2 001，B ＝⎣⎢⎡⎦⎥⎤1 004；(2)A ＝⎣⎢⎡⎦⎥⎤－1 0 0 －1，B ＝⎣⎢⎡⎦⎥⎤1234.解：(1)(AB )－1＝B －1A －1＝⎣⎢⎢⎡⎦⎥⎥⎤1 00 14⎣⎢⎢⎡⎦⎥⎥⎤12 00 1＝⎣⎢⎢⎡⎦⎥⎥⎤12 014. (2)(AB )－1＝B －1A －1＝⎣⎢⎢⎡⎦⎥⎥⎤－2132－12⎣⎢⎡⎦⎥⎤－100－1 ＝⎣⎢⎢⎡⎦⎥⎥⎤2－1－32 12. 5．变换矩阵A 把平面上的点P (2，－1)，Q (－1,2)分别变换成点P 1(3，－4)，Q 1(0,5)． (1)求变换矩阵A ；(2)判断变换矩阵A 是否可逆，如果可逆，求矩阵A 的逆矩阵A －1；如果不可逆，请说明理由．解：(1)设A ＝⎣⎢⎡⎦⎥⎤ab cd ，依题意，得⎣⎢⎡⎦⎥⎤ab cd ⎣⎢⎡⎦⎥⎤ 2－1＝⎣⎢⎡⎦⎥⎤ 3－4，⎣⎢⎡⎦⎥⎤ab cd ⎣⎢⎡⎦⎥⎤－1 2＝⎣⎢⎡⎦⎥⎤05，即⎩⎪⎨⎪⎧2a －b ＝3，2c －d ＝－4，－a ＋2b ＝0，－c ＋2d ＝5.解得⎩⎪⎨⎪⎧a ＝2，b ＝1，c ＝－1，d ＝2.所以A ＝⎣⎢⎡⎦⎥⎤21－12.(2)变换矩阵A 是可逆的，理由如下：设矩阵A 的逆矩阵为⎣⎢⎡⎦⎥⎤xy zw ，那么由⎣⎢⎡⎦⎥⎤ 2 1－1 2⎣⎢⎡⎦⎥⎤xy zw ＝⎣⎢⎡⎦⎥⎤1 00 1，得⎩⎪⎨⎪⎧2x ＋z ＝1，2y ＋w ＝0，－x ＋2z ＝0，－y ＋2w ＝1.解得⎩⎪⎪⎨⎪⎪⎧x ＝25，y ＝－15，z ＝15，w ＝25.故矩阵A 的逆矩阵为A－1＝⎣⎢⎢⎡⎦⎥⎥⎤25 －1515 25. 6．矩阵M ＝⎣⎢⎢⎡⎦⎥⎥⎤100 12，N ＝⎣⎢⎢⎡⎦⎥⎥⎤12 00 1，试求曲线y ＝cos x 在矩阵M －1N 对应的线性变换作用下的函数解析式．解：M －1＝⎣⎢⎡⎦⎥⎤1 002，∴M －1N ＝⎣⎢⎡⎦⎥⎤1 002⎣⎢⎢⎡⎦⎥⎥⎤12 00 1＝⎣⎢⎢⎡⎦⎥⎥⎤12 00 2. ∴⎣⎢⎡⎦⎥⎤x ′y ′＝⎣⎢⎢⎡⎦⎥⎥⎤12 00 2⎣⎢⎡⎦⎥⎤x y ＝⎣⎢⎢⎡⎦⎥⎥⎤12x 2y 即⎩⎪⎨⎪⎧x ′＝12x ，y ′＝2y .∴⎩⎪⎨⎪⎧x ＝2x ′，y ＝12y ′.代入y ＝cos x 得12y ′＝cos 2x ′故曲线y ＝cos x 在矩阵M －1N 对应的变换作用下解析式为y ＝2cos 2x . 7．矩阵A ＝⎣⎢⎡⎦⎥⎤1 234.(1)求矩阵A 的逆矩阵B ；(2)假设直线l 经过矩阵B 变换后的方程为y ＝x ，求直线l 的方程． 解：(1)设矩阵A 的逆矩阵为B ＝⎣⎢⎡⎦⎥⎤ab cd ，那么⎣⎢⎡⎦⎥⎤1 23 4⎣⎢⎡⎦⎥⎤ab cd ＝⎣⎢⎡⎦⎥⎤1 00 1，得⎩⎪⎨⎪⎧a ＋2c ＝1，b ＋2d ＝0，3a ＋4c ＝0，3b ＋4d ＝1，解得⎩⎪⎨⎪⎧a ＝－2，b ＝1，c ＝32，d ＝－12，所以B ＝⎣⎢⎢⎡⎦⎥⎥⎤－2132－12. (2)设直线l 上任一点P (x ，y )经过B 对应变换变为点P (x ′，y ′)，那么⎣⎢⎢⎡⎦⎥⎥⎤－2132－12⎣⎢⎡⎦⎥⎤x y ＝⎣⎢⎡⎦⎥⎤x ′y ′， 即⎩⎪⎨⎪⎧x ′＝－2x ＋y ，y ′＝32x －12y ，又y ′＝x ′，所以－2x ＋y ＝32x －12y ，即直线l 的方程为7x －3y ＝0.8．曲线C 在矩阵⎣⎢⎢⎡⎦⎥⎥⎤13 00 12对应的变换作用下的象为x 2＋y 2＝1，求曲线C 的方程．解：矩阵⎣⎢⎢⎡⎦⎥⎥⎤13 00 12对应的变换为：平面内点的纵坐标沿y 轴方向缩短为原来的12，横坐标沿x 轴方向缩短为原来的13，其逆变换为：将平面内点的纵坐标沿y 轴方向拉伸为原来的2倍，横坐标沿x 轴方向拉伸为原来的3倍，故⎣⎢⎢⎡⎦⎥⎥⎤13 00 12－1＝⎣⎢⎡⎦⎥⎤3 002.设圆x 2＋y 2＝1上任一点P (x ，y )在矩阵⎣⎢⎡⎦⎥⎤3002对应的伸缩变换作用下的象为P ′(x ′，y ′)，那么⎩⎪⎨⎪⎧x ′＝3x ，y ′＝2y ，即⎩⎪⎨⎪⎧x ＝13x ′，y ＝y ′2，代入x 2＋y 2＝1，得x ′29＋y ′24＝1.故曲线C 的方程为x 29＋y 24＝1.。