漂亮的雪花曲线.ppt
- 格式:ppt
- 大小:1.11 MB
- 文档页数:19

科赫曲线
简介
科赫曲线(Koch curve )是一种像雪花的几何曲线,所以又称为雪花曲线。
1904年瑞典数学家科赫第一次描述了这种不论由直段还是由曲段组成的始终保持连通的线,因此将这种曲线成为科赫曲线。
定义
设想一个边长为1的等边三角形,取每边中间的三分之一,接上去一个形状完全相似的但边长为其三分之一的三角形,结果是一个六角形。
现在取六角形的每个边做同样的变换,即在中间三分之一接上更小的三角形,以此重复,直至无穷。
外界的变得原来越细微曲折,形状接近理想化的雪花。
画法
1、任意画一个正三角形,并把每一边三等分;
2、取三等分后的一边中间一段为边向外作正三角形,并把这“中间一段”擦掉;
3、重复上述两步,画出更小的三角形。
4、一直重复,直到无穷,所画出的曲线叫做科赫曲线。
特性
1、它是一条连续的回线,永远不会自我相交。
2、曲线任何处不可导,即任何地点都是不平滑的。
3、曲线是无限长的,即在有限空间里的无限长度。
4、曲线上任意两点距离无穷大。
5、每次变化面积都会增加,但是总面积是有限的,不会超过初始三角形的外接圆。
思考
科赫曲线中产生一个匪夷所思的悖论:"无穷大"的边界,包围着有限的面积。
这让保守派数学大师们都很难相信。
科赫曲线是比较典型的分形图形,它具有严格的自相似特性。
提问:在有限面积里面,无穷的去选择无穷小的点来组成的"封闭"曲线.会包围着无穷大的面积吗?。


ppt如何制作雪花飞舞动画教程
wps是金山软件公司的一种办公软件,对日常办公起到了重要作用,那么大家对它的一些功能又有多少了解呢?比如用wps制作雪花动画,不懂的朋友没有关系,接下来店铺举例简单的例子告诉大家ppt 制作雪花动画的方法,欢迎大家来到店铺学习。
ppt制作雪花动画的方法
先将背景设置为黑色。
插入形状椭圆,填充为白色,设置柔化边缘。
为小圆添加动作路径-自由曲线,设置计时属性和效果属性。
复制多个雪点,显示高级日程表,调整出现的先后顺序。
5再复制很多个,并调整出现顺序,直到满意为止。


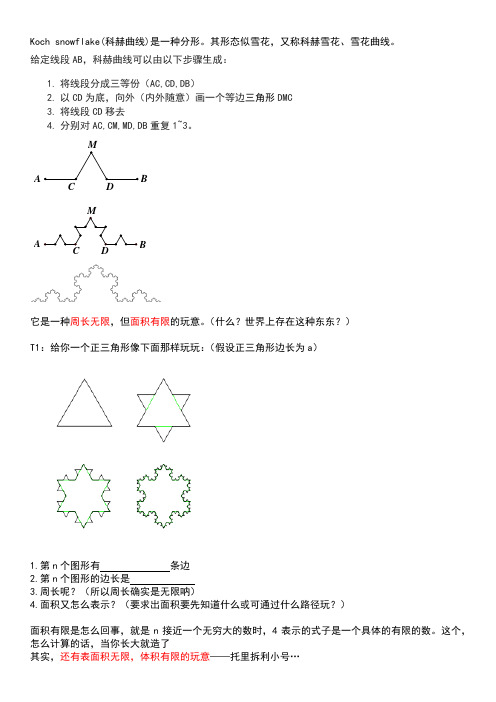
Koch snowflake(科赫曲线)是一种分形。
其形态似雪花,又称科赫雪花、雪花曲线。
给定线段AB ,科赫曲线可以由以下步骤生成: 1. 将线段分成三等份(AC,CD,DB )
2. 以CD 为底,向外(内外随意)画一个等边三角形DMC
3. 将线段CD 移去
4. 分别对AC,CM,MD,DB 重复1~3。
它是一种周长无限,但面积有限的玩意。
(什么?世界上存在这种东东?)
T1:给你一个正三角形像下面那样玩玩:(假设正三角形边长为a )
1.第n 个图形有条边
2.第n 个图形的边长是
3.周长呢?(所以周长确实是无限呐)
4.面积又怎么表示?(要求出面积要先知道什么或可通过什么路径玩?)
面积有限是怎么回事,就是n 接近一个无穷大的数时,4表示的式子是一个具体的有限的数。
这个,怎么计算的话,当你长大就造了
其实,还有表面积无限,体积有限的玩意——托里拆利小号… B
A B
A。
奇妙的“雪花曲线”
作者:丁学明
来源:《学与玩》2015年第01期
冬季里雪花漫天飞舞,你知道吗,雪不仅是文学艺术领域常常描绘的,也是数学的研究对象。
数学在不断更新和发展,其中,分形数学就是最近发展起来的一门新的数学分支,它第一次引起公众注意是1985年在《科学美国人》上发表的一篇文章,自那以后,分形数学的研究有了许多进展。
在分形数学中,最典型的当数“雪花曲线”了。
雪花曲线因其形状类似雪花而得名,雪花曲线又名科克曲线,它是在1906年由瑞典数学家赫尔奇·冯·科克第一次作出的。
雪花曲线是这样的:由图1那样的等边三角形开始,把三角形的每条边三等分,并在每条边三分后的中段向外作新的等边三角形,但要像图2那样去掉与原三角形叠合的边。
接着对每个等边三角形尖出的部分继续上述过程,即在每条边三分后的中段,像图3那样向外画新的尖形。
不断重复这样的过程,便产生了雪花曲线。
雪花曲线令人惊异的性质是:它具有有限的面积,但却有着无限的周长!我们可以这样想,在一张纸上画雪花曲线,不管“生长”多少次,它都不会超过一张纸的,所以说它的面积是有限的。
经过研究,其面积等于原三角形面积的1.6倍。
而雪花的边长可以无限地增加下去,所以说它的周长是无限的。
上面我们作的雪花曲线是向外作正三角形,如果我们向内作正三角形,则相应地得到如下图所示的另一系列的雪花曲线,称之为反雪花曲线。
下面就是应用分形数学原理画出的两个美丽的分形图形,你能设计出什么样的图形?请你也试着画一下。
用PPT制作雪花图案,太简单啦!教程很简单,总的来说就是画出雪花的一个分支,然后使用插件复制出剩下的部分。
下面就让我们开始吧!1、按住Shift键使用直线工具垂直的画出一条线段:2、在直线的一侧分别绘制出一条短线段和长线段:3、框选两条水平的线段,单击右键,选择“大小与位置”:4、在参数面板里设置旋转度数为50°,然后将两条旋转好的直线右对齐:为什么不直接斜着绘制直线呢?要先绘制再旋转呢?因为在PowerPoint中,旋转参数记录的是对象的旋转角度,而不是它固有的角度。
直接斜着绘制直线,再斜角度也是0°,因为它从未旋转过:没有了参数的比较,光靠眼睛来看,就不好保证两次绘制的斜线相互平行了。
5、将两条斜线移动过去,右端和垂直的线段相接。
然后将它们编为一组,结着复制一份,水平翻转后放到垂直的线段右侧,同样拼接起来。
注意翻转后进行位置调节时可以取消组合,只要保证翻转时两条斜线是一个组合即可:6、选中所有直线,设置颜色为白色,适当加粗,改变端点类型为“圆形”:7、复制出一份,将中间直线长度变短,放在一旁备用,原图形中的直线则可以适当加长:8、将原图形Ctrl+G编为一组,然后使用NT插件的环形复制功能复制出6份来,注意设置起始角度为30°,点选“自动旋转”:9、删除中间的原图形,将剩余6个图形编为一组。
然后使用椭圆工具绘制一个圆,设置为无填充,边线白色,磅数与之前设置的相同。
最后与刚才的组合图形上下、左右均做居中对齐:10、缩小前面变短了直线的那一个复制雪花花瓣,线条磅数也可以适当减小,然后再绘制大小不一的三个圆叠放在雪花花瓣顶上:11、将上一步得到的形状编为一组,放置到雪花中央(可以对三组形状使用上下、左右居中对齐命令来确保形状位于中心位置):12、再次是用NT的环形复制命令,将小雪花花瓣复制6份,自动旋转,与上一次唯一的不同是,这次维持起始角度为0°:13、删除中间的原始雪花花瓣,使用十二角星工具绘制出一个白色的十二角星,放置到雪花中央圆圈内,同样注意居中对齐:根据你的喜好,可以缩放调节十二角星的大小,以及拖动黄色的控点来调节角的尖锐程度。
雪花曲线
雪花曲线因其形状类似雪花而得名,它的产生假定也跟雪花类似.
由图1 那样的等边三角形开始.然后把三角形的每条边三等分,并在每条边三分后的中段向外作新的等边三角形,但要像图2那样去掉与原三角形叠合的边.接着对每个等边三角形尖出的部分继续上述过程,即在每条边三分后的中段,像图3那样向外画新的尖形.不断重复这样的过程,便产生了雪花曲线.
雪花曲线令人惊异的性质是:它具有有限的面积,但却有着无限的周长!
雪花曲线的周长持续增加而没有界限,但整条曲线却可以画在一张
倍.。