悬 臂 梁 的 有 限 元 分 析

《有限元方法》2023年课程大作业*名：***学号：XS********指导老师：**教授*********大学二〇二三年五月目录1作业内容与要求 (2)2考虑剪切变形空间梁的势能泛函和梁单元位移插值函数，并通过泛函变分原理推导得到梁单元的刚度方程 (2)3、给出matlab编写的有限元程序源代码以及对应的说明，包括 (5)1) 有限元程序整体架构，计算的流程图； (5)2) 离散化与编号； (8)3) 数据的准备； (8)4) 单元分析形成单元刚度矩阵； (11)5) 组装整体刚度矩阵； (13)6) 节点载荷的计算； (14)7) 边界条件的处理及刚度方程求解； (17)8) 应力和应变的计算；.......................................................... 错误!未定义书签。

9) 和无开口梁情况分析比较 (18)10) 结论。

(20)1作业内容与要求如图1所示，某悬臂梁，有三个矩形开口，梁端承受一集中载荷F ，大小为60000N 。

试采用考虑剪切变形的2结点空间梁单元，用matlab 编写有限元程序，计算梁端A 点的线位移，并和无开口梁的结果进行比较。

悬臂梁材料的杨氏模量，泊松比。

图1 矩形开口悬臂梁结构末端受集中力F 作用示意图要求：一、纸质报告A4单面打印，随笔试答卷一起上交； 二、报告格式要求同研究生学位论文；2考虑剪切变形空间梁的势能泛函和梁单元位移插值函数，并通过泛函变分原理推导得到梁单元的刚度方程首先把空间梁单元分解成一个杆单元、一个轴单元，和xoy ，xoz 平面内的两个平面梁，由此可以吧得到空间梁单元的能量泛函为：22200022200000111Π(,,,)d d d 222111d ()d ()d 222 d d l l l x y xoz xoz z xoy xoz l l l x xoy xoy l l z z j iz i z jimj GA u v w EI x x EI x k d GA du x EA x JG x k dx dxq w x P w M qv x P θκγκθγθ=⎰+⎰+⎰+⎰+⎰+⎰-⎰-∑+∑-⎰-∑00 d -d ym m n n l l x z l x x k x k xknl lv M f u x F u m x M θθθ+∑⎰-∑-⎰-∑ (1)首先给出如下的形函数（插值函数）()()23123322332334561322321N N l N N l N N ξξξξξξξξξξξ=-+=-+=-=-+=-= (2)其中,01ix x lξξ-=≤≤ (3)对于考虑剪切变形的梁单元将挠度分解为b S w w w =+(4)则节点位移为112212b e b b s es s w q w w q w θθ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎡⎤=⎢⎥⎣⎦(5)其中1212d d ,d d b b w w x x θθ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭(6)考虑将s w 采用2结点的Lagrange 插值，即线性插值； bw 采用与不考虑剪切变形梁单元的w 相同的Hermite 插值，则有112132425162b b bsss w N w N N w N w N w N w θθ=+++=+ (7)利用平衡方程将sw 凝聚掉，可以得到最终平面梁单元的能量泛函为1Π()2Te q q K q Fq =- 其中()()11222321220[,,,]1261266(4)6(2)126126(1)6(2)6(4)d //e e T T Tj j b l k l l l b l l b l EI K l l b l l b l l b w l P N ql N P dN d M q lw ξξξθθξ-⎡⎤⎢⎥+--⎢⎥=⎢⎥---+⎢⎥--+⎣⎦=⎰+∑-∑⋅= (8)对于杆单元5162u N u N u =+(9)杆单元的能量泛函为1Π()2Te q q K q Fq =- 其中Ke 杆的刚度矩阵()02111111[,]d e T Tx j j x EA Ke l P N ql N P q u u ξξ-⎛⎫=⎪-⎝⎭=⎰+∑= (10)同理可以得到轴的5162x N N θθθ=+(11)能量泛函为1Π()2Te q q K q Fq =- 其中Ke 杆的刚度矩阵()02111111[,]d e T Tx j j x GJ Ke lP N ql N P q θξθξ-⎛⎫=⎪-⎝⎭=⎰+∑= (12)最后将这些进行组合可以得到总的能量泛函为 1Π()2T e q q K q Fq =-(13)其中3333333322333323126126(1)(1)(1)(1)126126(1)(1)(1)(1)6(4)6(2)(1)(1)(1)(1)6(4)(1)(1)z z z z y y y y yy y y z z EAEA l lEI lEI EI lEI b l b l b l b l EI lEI EI lEI b l b l b lb l GJ GJl llEI b l EI lEI b l EI b l b l b l b l lEI b l EI b l b --++++---++++-+--+++++++23333333333322333(2)6(1)(1)126126(1)(1)(1)(1)126126(1)(1)(1)(1)((2)(4)6(1)(1)(1)6(y z z z z z y y y y y y z z b l EI lEI l b l b l EA EA l lEI lEI EI lEI b l b l b l b l EI lEI EI lEI b l b l b l b l GJGJ l lb l EI b l EI lEI b l b l b l lEI --++---++++-++++---+-+++3111111222222223333((2)66(4)1 [,,,,,,,,,)(1)(1)(1,,)(1)z z z z x y z x y z b l E u I lEI lEI b l EI b l b l b l b l b w l q v u v w θθθθθθ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-+-+++++⎥⎢⎥⎢⎣⎦=](14)对能量泛函1Π()2Teq q K q Fq=-取变分为零即Π()0eq K q F=-=(15)即空间梁单元的刚度方程3、给出matlab编写的有限元程序源代码以及对应的说明，包括1) 有限元程序整体架构，计算的流程图；程序的流程图如下图所示global E mu G; %将泊松比和杨氏模量声明为全局变量E = 2.0e11; %给杨氏模量赋予指定值mu = 0.25; %给泊松比赋予指定值G = E/(1+mu)/2; %有泊松比杨氏模量计算剪切模量L=[15,30,15,30,15,30,15]*10^(-2);A=[30*10,15*10,30*10,15*10,30*10,15*10,30*10]*10^(-4);Iy=[10*(30^3),10*(30^3)-10*(15^3),10*(30^3),10*(30^3)…-10*(15^3),10*(30^3),10*(30^3)-10*(15^3),10*(30^3)]/12*10^(-8);2) 离散化与编号；在本次作业中根据梁的截面变化将梁分成七个单元从左到右依次编号为①②③④…⑦,为了保证最后组集得到最终刚度矩阵的稀疏性，减小存储矩阵的半带宽，节点编号也是采用从左到右依次1,2,3,4，…8的编号方法，具体离散化和单元以及节点编号的示意图如下图所示：图一、悬臂梁单元的离散以及单元节点编号示意图这一部分程序体现在main—function主函数中。

悬臂梁受力分析报告高一博2016.11.13西安理工大学机械与精密仪器工程学院摘要利用ANSYS对悬臂梁进行有限元静力学分析,得到悬臂梁的最大应力和挠度位移。

从而校验结构强度和尺寸定义，从而对结构进行最优化设计修正。

关键词：悬臂梁，变形分析，应力分析目录一.问题描述： (4)二.分析的目的和内容： (4)三.分析方案和有限元建模方法： (4)四.几何模型 (4)五．有限元模型 (4)六．计算结果： (5)七.结果合理性的讨论、分析 (8)八．结论 (8)参考文献 (8)一.问题描述：现有一悬臂梁，长500MM，一端固定，另外一端施加一个竖直向下的集中力200N。

其截面20MMX20MM的矩形，现在要分析该梁的在集中力作用下产生的位移，应力和局部应力。

二.分析的目的和内容：1.观察悬臂梁的变形情况；2.观察分析悬臂梁的应力变化；3.找出其最大变形和最大应力点，分析形成原因；三.分析方案和有限元建模方法：1.使用ANSYS-modeling-create-volumes-block建模，2.对梁进行材料定义，网格划分。

3.一端固定，另外一端施加一个向下的200N的力。

4.后处理中查看梁的应力和变形情况。

四.几何模型500X20X20的梁在在ANSYS中进行绘制.由于结构简单规则，无需简化。

五．有限元模型单元类型：solid brick8node45材料参数：弹性模量2e+11pa,泊松比0.3边界条件：一端固定，一端施加载荷载荷：F=200N划分网格后的悬臂梁模型六．计算结果：变形位移图等效应力图局部应力图七.结果合理性的讨论、分析1.位移分析：在变形位移图上，在约束端位移最小为零，受压端位移最大。

与实际结果一致。

2.应力分析：在应力图上，应力最大处在约束端，而最小的位于受压端，与变形图相对应。

通过材料力学计算可知约束端的所受弯矩最大。

两个结果印证无误。

3.局部应力分析：在局部应力图上，可以看出在固定端上表面存有较大的应力，且为拉应力，受压端直角尖处有最大应力，从形成原因上分析属于尖角处应力集中。

可编辑修改精选全文完整版有限元分析中的结构静力学分析怎样才能做好1 概述结构有限元分析中，最基础、最根本、最关键、最核心同时也是最重要的一种分析类型就是“结构静力学分析”。

静力学分析可用于与结构相关、与流体相关、与电磁相关以及与热相关的所有产品；静力学分析是有限元分析的根基，是有限元分析的灵魂。

2 基础理论结构静力学按照矩阵的形式可表示为微分方程：[K]{x}+{F}=0其中，[K]代表刚度矩阵，{x}代表位移矢量，{F}代表静载荷函数。

由此可知，结构静力学有限元分析过程就是求解微分方程组的过程。

2.1 三个矩阵的说明静力学分析微分方程组三个矩阵进一步说明：[K]代表刚度矩阵。

举例说明，如果用手折弯一根筷子，假设筷子是钢材料的，比较硬，很难折断；假设筷子是常规木材的，比较脆，基本上都能折断。

这里筷子断与不断的本质并不是钢或者木材，而是钢或者木材表在筷子上表现出来的刚度（或者叫硬度），这里刚度用计算机数值分析的方式来描述，就是刚度矩阵。

{x}代表位移矢量。

举例说明，一把椅子，如果有人偏瘦，坐在椅子上，椅面基本不下沉；如果有人偏胖，坐在椅子上，椅面会有明显下沉（谁坐谁知道...），此时，椅面的下沉量，可用位移矢量来表示。

{F}代表静载荷函数，也是静力学分析的关键。

举例说明，上面筷子例子中，手腕对筷子的作用，就是一种载荷（或者叫外力、荷载、负荷、承重等）；上面椅子例子中，人对椅子表面的作用，也是一种载荷。

这些载荷在大多数情况下，没有明显的快慢效应，就可用静载荷函数来表示。

2.2 静力学分析中的载荷说明静载荷函数本质说明：假设1，相同一根筷子，又假设筷子比较粗（或者说是几根筷子捆绑在一起）：双手慢慢用1 / 5力，筷子难断；双手快速用力，筷子难断，此时慢慢折弯的效果就可以理解为静力学过程。

假设2，相同椅子：慢慢坐下去，椅子没有明显晃动；快速坐下去，椅子没有明显下沉与晃动，此时慢慢坐在椅子上的过程就可以理解为静力学过程。

悬臂梁结构动力响应分析与优化设计悬臂梁是一种常见的结构形式，在工程中有广泛的应用。

然而，由于其特殊的结构特点，悬臂梁在受到外界力作用时容易发生动力响应，影响其安全性和稳定性。

因此，对悬臂梁结构进行动力响应分析与优化设计，对于确保结构的安全性和可靠性至关重要。

悬臂梁结构的动力响应分析是指通过数学建模和计算分析对悬臂梁在受到外界力作用下的响应情况进行评估。

在进行动力响应分析时，需要考虑诸如结构的质量、刚度等参数。

通常，可以利用有限元方法对悬臂梁进行动力响应分析。

有限元方法是一种通过将结构离散为有限个小单元，然后对每个小单元进行力学计算，并将计算结果进行组合得出整体结构响应的数值计算方法。

通过有限元分析，可以得出悬臂梁受力情况、变形情况等重要参数，对于结构的合理设计和改进提供科学依据。

在动力响应分析的基础上，进行悬臂梁结构的优化设计是为了提高其动力响应性能。

悬臂梁的优化设计要考虑多个因素，包括结构的材料性能、几何形状、截面尺寸等。

在材料性能方面，通常需要选择具有较高强度和刚度的材料，以保证结构的承载能力。

在几何形状和截面尺寸方面，通过合理选择和设计，可以减小结构的质量和惯性矩，从而降低悬臂梁的动力响应。

对于悬臂梁结构的优化设计，常见的方法是结构拓扑优化和参数优化。

结构拓扑优化通过改变梁的支座位置、截面形状等来优化悬臂梁结构。

参数优化则是在已定形状的基础上，优化截面尺寸、材料性能等参数，以达到优化结构动力响应的效果。

这两种方法既可以分开进行也可以结合使用，通过多次计算和比较来找到最优的结构设计方案。

悬臂梁结构动力响应分析与优化设计是一个综合性和复杂性的工程问题。

在实际工程中，需要综合考虑结构的静力和动力响应，还要考虑材料的可获得性、成本等因素。

因此，对悬臂梁结构进行动力响应分析与优化设计需要多学科的知识和专业工具的支持。

只有通过科学的方法和综合考虑各种因素，才能得到结构性能和经济性的双重保证。

总之，悬臂梁结构动力响应分析与优化设计对于确保结构的安全性和可靠性具有重要意义。

第五章 悬臂梁桥简介钢筋混凝土简支梁桥，由于构造简单，预制和安装方便，在桥梁建设中得到了广泛使用。

然而这种简支体系当跨径超过20～25m时，鉴于跨中恒载弯矩和活载弯矩将迅速增大，致使梁的截面尺寸和自重显著增加，这样不但材料耗用量大而不经济，并且很大的安装重量也给装配式施工造成困难。

因此，对于较大跨径的桥梁，为了降低材料用量指标，就宜采用能减小跨中弯矩值的其他体系桥梁，如悬臂体系和连续体系梁桥等。

本章内将主要介绍悬臂梁桥的力学特点、一般构造特点及其设计要点，以便在掌握简支梁桥构造和设计的基础上，从力学和混凝土原理等方面知识出发，进一步了解和掌握这类体系桥的计算和设计工作。

5.1 悬臂梁桥结构类型和力学特点5.1.1 悬臂梁桥结构类型将简支梁梁体加长延伸，并越过支点就成为悬臂梁桥。

我们把梁的一端悬出和两端均悬出分别称为单悬臂梁和双悬臂梁。

常见的类型有：双悬臂梁桥（图5.2a）、两个单悬臂梁与中孔简支挂梁组合的三跨悬臂梁桥（图5.2b）、双悬臂梁（或单悬臂梁）与简支挂梁联合组成多孔悬臂梁桥（图5.2c），以及带挂梁的T形悬臂梁桥（图5.1d，即带挂梁的T形刚构）。

根据桥长的需要可选用不同的类型。

通常将悬臂梁主跨称为锚跨。

多孔悬臂梁桥的结构特点是锚跨与挂孔跨交替布置,通常为奇数跨布置。

5.1.2 悬臂梁桥力学特点悬臂梁桥利用悬出支点以外的伸臂，使支点产生负弯矩，对锚跨跨中正弯矩产生有利的卸载作用。

图 5.1所示为各种梁式体系在恒载作用下的弯矩图。

图中各种梁式体系的跨径布置相同，假定其恒载集度也相同（实际上，简支梁的恒载集度较大）。

比较图5.1中a）与b）、c），显然，简支梁的各跨跨中恒载弯矩最大，无论单悬臂梁或双悬臂梁在锚跨跨中弯矩因支点负弯矩以卸载作用而显著减小，而悬臂跨中因简支挂梁的跨径缩短而跨中正弯矩也同样显著减小。

悬臂梁桥的弯矩图面积(反映材料用量)也比简支梁桥小，以图5.1 c)的中跨弯矩图为例，当悬臂长度等于中孔跨径的四分之一时，正负弯矩图面积的总和仅为同跨径简支梁的1／3.2。

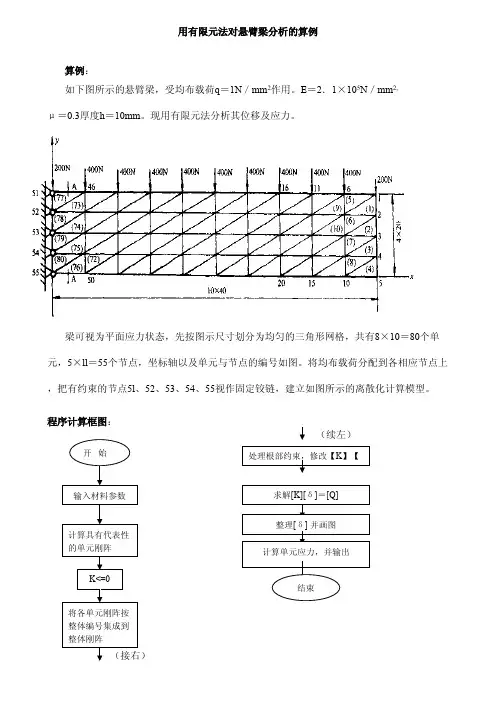
用有限元法对悬臂梁分析的算例算例：如下图所示的悬臂梁，受均布载荷q ＝1N ／mm 2作用。

E ＝2．1×105N ／mm 2,μ＝0.3厚度h ＝10mm 。

现用有限元法分析其位移及应力。

梁可视为平面应力状态，先按图示尺寸划分为均匀的三角形网格，共有8×10＝80个单元，5×ll ＝55个节点，坐标轴以及单元与节点的编号如图。

将均布载荷分配到各相应节点上，把有约束的节点5l 、52、53、54、55视作固定铰链，建立如图所示的离散化计算模型。

程序计算框图：（续左）程序中的函数功能介绍及源代码1.LinearTriangleElementStiffness(E,NU,t,xi,yi,xj,yj,xm,ym)――该函数用于计算平面应力情况下弹性模量为E、泊松比为NU、厚度为t、第一个节点坐标为(xi,yi)、第二个节点坐标为(xj,yj)、第三个节点坐标为(xm，ym)时的线性三角形元的单元刚度矩阵.该函数返回6×6的单位刚度矩阵k.2.LinearTriangleAssemble(K,k,i,j,m)――该函数将连接节点i,j,m的线性三角形元的单元刚度矩阵k集成到整体刚度矩阵K。

每集成一个单元，该函数都将返回2N×2N的整体刚度矩阵K.3.LinearTriangleElementStresses(E,NU,t,xi,yi,xj,yj,xm,ym,u)-- 该函数计算在平面应力情况下弹性模量为E、泊松比为NU、厚度为t、第一个节点坐标为(xi, yi)第二个节点坐标为(xj,yj)、第三个节点坐标为(xm，ym)以及单元位移矢量为u时的单元应力。

该函数返回单元应力矢量。

函数源代码：function y = LinearTriangleElementStiffness(E,NU,t,xi,yi,xj,yj,xm,ym)A = (xi*(yj-ym) + xj*(ym-yi) + xm*(yi-yj))/2;%三角形单元面积，单元节点应该按逆时针排序，保证每个三角形单元的面积都为正值（也可作为一个小函数：LinearTriangleElementArea）betai = yj-ym;betaj = ym-yi;betam = yi-yj;gammai = xm-xj;gammaj = xi-xm;gammam = xj-xi;B = [betai 0 betaj 0 betam 0 ;0 gammai 0 gammaj 0 gammam ;gammai betai gammaj betaj gammam betam]/(2*A);%B为应变矩阵，其中betai=yi-ym,betaj=ym-yi,betam=yi-yj.gammai=xm-xj, gammaj=xi-xm, gammam=xj-xi.D = (E/(1-NU*NU))*[1 NU 0 ; NU 1 0 ; 0 0 (1-NU)/2];%D为弹性矩阵，分为平面应力问题和平面应变问题对于平面应力问题D = (E/(1-NU*NU))*[1 NU 0 ; NU 1 0 ; 0 0 (1-NU)/2];对于平面应变问题E1=E/（1-NU*NU），NU1=NU/（1-NU）y = t*A*B'*D*B;%单元刚度矩阵function y = LinearTriangleAssemble(K,k,i,j,m)K(2*i-1,2*i-1) = K(2*i-1,2*i-1) + k(1,1); K(2*i-1,2*i) = K(2*i-1,2*i) + k(1,2);K(2*i-1,2*j-1) = K(2*i-1,2*j-1) + k(1,3); K(2*i-1,2*j) = K(2*i-1,2*j) + k(1,4);K(2*i-1,2*m-1) = K(2*i-1,2*m-1) + k(1,5); K(2*i-1,2*m) = K(2*i-1,2*m) + k(1,6);K(2*i,2*i-1) = K(2*i,2*i-1) + k(2,1); K(2*i,2*i) = K(2*i,2*i) + k(2,2);K(2*i,2*j-1) = K(2*i,2*j-1) + k(2,3); K(2*i,2*j) = K(2*i,2*j) + k(2,4);K(2*i,2*m-1) = K(2*i,2*m-1) + k(2,5); K(2*i,2*m) = K(2*i,2*m) + k(2,6);K(2*j-1,2*i-1) = K(2*j-1,2*i-1) + k(3,1); K(2*j-1,2*i) = K(2*j-1,2*i) + k(3,2);K(2*j-1,2*j-1) = K(2*j-1,2*j-1) + k(3,3); K(2*j-1,2*j) = K(2*j-1,2*j) + k(3,4);K(2*j-1,2*m-1) = K(2*j-1,2*m-1) + k(3,5); K(2*j-1,2*m) = K(2*j-1,2*m) + k(3,6);K(2*j,2*i-1) = K(2*j,2*i-1) + k(4,1); K(2*j,2*i) = K(2*j,2*i) + k(4,2);K(2*j,2*j-1) = K(2*j,2*j-1) + k(4,3); K(2*j,2*j) = K(2*j,2*j) + k(4,4);K(2*j,2*m-1) = K(2*j,2*m-1) + k(4,5); K(2*j,2*m) = K(2*j,2*m) + k(4,6);K(2*m-1,2*i-1) = K(2*m-1,2*i-1) + k(5,1); K(2*m-1,2*i) = K(2*m-1,2*i) + k(5,2);K(2*m-1,2*j-1) = K(2*m-1,2*j-1) + k(5,3); K(2*m-1,2*j) = K(2*m-1,2*j) + k(5,4);K(2*m-1,2*m-1) = K(2*m-1,2*m-1) + k(5,5); K(2*m-1,2*m) = K(2*m-1,2*m) + k(5,6);K(2*m,2*i-1) = K(2*m,2*i-1) + k(6,1); K(2*m,2*i) = K(2*m,2*i) + k(6,2);K(2*m,2*j-1) = K(2*m,2*j-1) + k(6,3); K(2*m,2*j) = K(2*m,2*j) + k(6,4);K(2*m,2*m-1) = K(2*m,2*m-1) + k(6,5); K(2*m,2*m) = K(2*m,2*m) + k(6,6);K;%对号入座，如前所述，每集成一次都将返回2N×2N的整体刚度矩阵K.此题为110×110 function y = LinearTriangleElementStresses(E,NU,t,xi,yi,xj,yj,xm,ym,u)A = (xi*(yj-ym) + xj*(ym-yi) + xm*(yi-yj))/2;betai = yj-ym;betaj = ym-yi;betam = yi-yj;gammai = xm-xj;gammaj = xi-xm;gammam = xj-xi;B = [betai 0 betaj 0 betam 0 ;0 gammai 0 gammaj 0 gammam ;gammai betai gammaj betaj gammam betam]/(2*A);D = (E/(1-NU*NU))*[1 NU 0 ; NU 1 0 ; 0 0 (1-NU)/2];%平面应力和平面应变问题两种情况y = D*B*u;%单元应力计算主程序源代码E=21e7;NU=0.3;t=0.01;stifflike5=LinearTriangleElementStiffness(E,NU,t,0.4,0.08,0.36,0.08,0.36,0.06,1) %选取2个基本单元，调用M文件stifflike1=LinearTriangleElementStiffness(E,NU,t,0.4,0.08,0.36,0.06,0.4,0.06,1) K=sparse(110,110); %creat a xishu matrix for total stiff创建一个稀疏矩阵for i=1:49if rem(i,5)%模取余，bool型变量，非零即为真j=i;K=LinearTriangleAssemble(K,stifflike5,j,j+5,j+6);%节点编号K=LinearTriangleAssemble(K,stifflike1,j,j+6,j+1);endend%将每个单元刚度矩阵集成到总刚中K=full(K);%转化稀疏矩阵 k=K(1:100,1:100);k=[K,zeros(100,10);zeros(10,100),eye(10)];k=sparse(k);%利用边界条件简化基本方程Q=sparse(2:10:92,1,[-200,-400,-400,-400,-400,-400,-400,-400,-400,-400,],110,1);%外部荷载，此处不包括约束条件，通过形函数确定，是不是可以理解为梁的两端为中间的一半呢？d=k\Q;%高斯消元法，比克莱姆法则在计算速度上有绝对的优势！x=0:0.04:0.4;plot(x,d(106:-10:6))%基本绘图命令grid%带网格y=zeros(80,3);q=0;for i=1:49switch rem(i,5)case 1j=2*i;u=[d(j-1) d(j) d(j+11) d(j+12) d(j+1) d(j+2)];u=u';xl=0.4;yl=0.08;xm=0.36;ym=0.06;xn=0.4;yn=0.06;y(i+q,:)=LinearTriangleElementStresses(E,NU,t,xl,yl,xm,ym,xn,yn,u)';xl=xl-0.04;xm=xm-0.04;xn=xn-0.04;case 2j=2*i;u=[d(j-1) d(j) d(j+11) d(j+12) d(j+1) d(j+2)];xl=0.4;yl=0.06;xm=0.36;ym=0.04;xn=0.4;yn=0.04;y(i+q,:)=LinearTriangleElementStresses(E,NU,t,xl,yl,xm,ym,xn,yn,u)'; xl=xl-0.04;xm=xm-0.04;xn=xn-0.04;case 3j=2*i;u=[d(j-1) d(j) d(j+11) d(j+12) d(j+1) d(j+2)];u=u';xl=0.4;yl=0.04;xm=0.36;ym=0.02;xn=0.4;yn=0.02;y(i+q,:)=LinearTriangleElementStresses(E,NU,t,xl,yl,xm,ym,xn,yn,u)'; xl=xl-0.04;xm=xm-0.04;xn=xn-0.04;case 4j=2*i;u=[d(j-1) d(j) d(j+11) d(j+12) d(j+1) d(j+2)];u=u';xl=0.4;yl=0.02;xm=0.36;ym=0;xn=0.4;yn=0;y(i+q,:)=LinearTriangleElementStresses(E,NU,t,xl,yl,xm,ym,xn,yn,u)'; xl=xl-0.04;xm=xm-0.04;xn=xn-0.04;otherwiseq=q+3;endendq=4;for i=1:49switch rem(i,5)case 1j=2*i;u=[d(j-1) d(j) d(j+9) d(j+10) d(j+11) d(j+12)];u=u';xl=0.4;yl=0.08;xm=0.36;ym=0.08;xn=0.36;yn=0.06;y(i+q,:)=LinearTriangleElementStresses(E,NU,t,xl,yl,xm,ym,xn,yn,u)'; xl=xl-0.04;xm=xm-0.04;xn=xn-0.04;case 2j=2*i;u=[d(j-1) d(j) d(j+9) d(j+10) d(j+11) d(j+12)];u=u';xl=0.4;yl=0.06;xm=0.36;ym=0.06;xn=0.36;yn=0.04;y(i+q,:)=LinearTriangleElementStresses(E,NU,t,xl,yl,xm,ym,xn,yn,u)'; xl=xl-0.04;xm=xm-0.04;xn=xn-0.04;case 3j=2*i;u=[d(j-1) d(j) d(j+9) d(j+10) d(j+11) d(j+12)];u=u';xl=0.4;yl=0.04;xm=0.36;ym=0.04;xn=0.36;yn=0.02;y(i+q,:)=LinearTriangleElementStresses(E,NU,t,xl,yl,xm,ym,xn,yn,u)'; xl=xl-0.04;xm=xm-0.04;xn=xn-0.04;case 4j=2*i;u=[d(j-1) d(j) d(j+9) d(j+10) d(j+11) d(j+12)];u=u';xl=0.4;yl=0.02;xm=0.36;ym=0.02;xn=0.36;yn=0;y(i+q,:)=LinearTriangleElementStresses(E,NU,t,xl,yl,xm,ym,xn,yn,u)';xl=xl-0.04;xm=xm-0.04;xn=xn-0.04;otherwiseq=q+3;endend %y(i+q,:)这是实现什么的？没见过这种用法，算法上应该就是通过节点位移实现指定单元的内力，这部分本人看的也晕晕的，望高人指点N=y(73:80,1)结果图及数据输出悬臂梁轴线挠度图：一单元的单元刚阵1.0e+006 *0.8077 0 0 -0.4038 -0.8077 0.40380 2.3077 -0.3462 0 0.3462 -2.30770 -0.3462 0.5769 0 -0.5769 0.3462-0.4038 0 0 0.2019 0.4038 -0.2019-0.8077 0.3462 -0.5769 0.4038 1.3846 -0.75000.4038 -2.3077 0.3462 -0.2019 -0.7500 2.5096五单元的单元刚阵1.0e+006 *00.050.10.150.20.250.30.350.4x/m w /m0.5769 0 -0.5769 0.3462 0 -0.34620 0.2019 0.4038 -0.2019 -0.4038 0-0.5769 0.4038 1.3846 -0.7500 -0.8077 0.34620.3462 -0.2019 -0.7500 2.5096 0.4038 -2.30770 -0.4038 -0.8077 0.4038 0.8077 0-0.3462 0 0.3462 -2.3077 0 2.3077根部73-80各单元应力计算结果如下（n/m2）：1.0e+007 *2.1119 -0.0621 -2.2816 -4.8824 5.0479 2.4065 0.0352 -2.3753。

基于ANSYS 10.0对悬臂梁的强度及变形分析姓名：***班级：机制0803班学号：************对悬臂梁的受力及变形分析摘要：本研究分析在ANSYS10.0平台上，采用有限元法对悬臂梁进行强度与变形分析、验证此悬臂梁设计的合理性。

一、问题描述长度L=254 mm的方形截面的铝合金锥形杆，上端固定，下端作用有均布拉力P=68.9 Mpa，上截面的尺寸50.8×50.8 mm，下截面尺寸25.4×25.4 mm（见右图），弹性模量E=7.071×104 Mpa，泊松比μ=0.3，试用确定下端最大轴向位移δ和最大轴向应力。

试将分析结果与理论解进行比较，说明有限元分析的误差。

（理论解：最大轴向位移δ=0.1238 mm）。

二、建立有限元模型：定义模型单元类型为：solid（实体）95号单元，材料常数为：弹性模量E=7.071×104 Mpa，泊松比μ=0.3。

三、有限元模型图：建立有限元模型时，观察模型的形状可知，我们可以先建立模型的上下底面，再根据有上下底面形成的八个关键点（keypoints）生成线，接着生成面，生成体。

最后生成该悬臂梁的模型图，示图如下：整个模型建立好之后即可对其划分网格，划分网格时，若选择自由划分则生成的网格比较混乱，不能比较准确的模拟该梁真实的受力变形情况。

故我们选择智能划分模式，并且分别对模型的各个棱边（lines）进行均匀分割，这样可以划分出比较理想的网格，更利于我们的研究和分析。

网格划分之后的模型图为：四、加载并求解：根据该悬臂梁的受力特点，我们在其下底面（比较大的底面）上进行六个自由度的位移约束，而在其上地面上施加大小为P=68.9 Mpa均布拉力，将载荷加载好之后便可进行运算求解，求解完成之后，我们得到其位移变形图如下：Z向位移云图为：Z向应力云图为：五、结果分析及结论：由以上两张云图和一张变形图中我们可以读出，悬臂梁的最大轴向（Z向）位移和轴向（Z向）最大应力分别为：最大轴向位移为：δ=0.123746 mm 最大轴向应力为：σ=68.224 Mpa 但是，我们知道，如果所划分的网格有差异时，计算结果将会产生一定的误差，由于设计要求的最大轴向位移不能超过0.1238mm，而我们的建模计算结果已经小于此设计要求值。

２．２有 限元 网格 处理 速度 的提升
Ｃｎｔｒｌｓ—｝ＭａｎｕａｌＳｉｚｅ＿ Ｌｉｎｅｓ—｝ＡＵ Ｌｉｎｅｓ
有 限元分 析 过程 主要 包含 了三 个 步骤 ：对 分 析对 象进 行 离 ＡＮＳＹＳ Ｍａ ｉｎ Ｍｅｎｕ： Ｐｒｅｐｒｏｃｅｓｓｏｒ ＿＋ Ｍｅｓｈｉｎｇ－＋ＭｅｓｈｒＩ ｌ
２０１８．２６科 学技 术创新 一１２３一
基 于有 限元软 件 ＡＮＳＹＳ分析 简单悬臂 梁 的模 型
郭安 江 （安徽理工大学 土木建筑学院，安徽 淮南 ２３２００１）
摘 要：作为 目前世界上发展最快的计算机辅助工程（ｃＡＥ）工具 ，ＮＳＹＳ软件的接 口可 以与大多数计算机辅助 工程（ｃＡＥ）工具
关键 词 ：ＡＮＳＹＳ软件 ；有 限元 ；线 性 ；悬臂 梁
中 图 分 类 号 ：ＴＵ３７５．１
文 献 标 识 码 ：Ａ
文章 编号 ：２０９６－４３９０（２０１８）２６－０１２３—０２
１ ＡＮＳＹＳ软 件简 介
于应用线性理论来解决破坏 、裂纹扩展等问题 ，还需要解决材料
为了验证某机械结构系统是否满足安全性等设计需求 ，我 的塑形和蠕变效应 ，此时必须求解材料的非线性问题 ，例如对塑
连接。计算机辅助设计软件相对应 ，为数据的共享和交流提供 了便利 ，例如 Ｃｒｅｏ，ＮＡＳＴＲＡＮ，Ｉ－ＤＥＡＳ，ＡｕｔｏＣＡＤ等软件 。ＡＮＳＹＳ
软件 。包含 了多种有限元分析软件的功能 ，从 简单的线性静 力分析到非常复杂的非线性动 力分析 ，再到电磁 分析、流体分析 、热分
析等。在每一个不同的工程领域 ，ＡＮＳＹＳ软件分析方法有所差别 ，步骤也不一样。本文主要分析简单悬臂梁的有限元模型。
散化 处理 、有 限元求 解 、对计 算 结果 进行 后处 理 。过 去 由于计 算 Ｍｅｓｈ：ｌｉｎｅｓ

线性静力学分析实例—-以悬臂梁为例线性静力学问题是简单且常见的有限元分析类型，不涉及任何非线性(材料非线性、几何非线性、接触等）,也不考虑惯性及时间相关的材料属性。

在ABAQUS 中,该类问题通常采用静态通用（Ｓta ｔi ｃ,Gen ｅr ａｌ)分析步或静态线性摄动(Sta ｔi ｃ,Ｌi ｎear p ｅrturbation ）分析步进行分析。

线性静力学问题很容易求解,往往用户更关系的是计算效率和求解效率，希望在获得较高精度的前提下尽量缩短计算时间，特别是大型模型。

这主要取决于网格的划分，包括种子的设置、网格控制和单元类型的选取。

在一般的分析中,应尽量选用精度和效率都较高的二次四边形/六面体单元,在主要的分析部位设置较密的种子；若主要分析部位的网格没有大的扭曲,使用非协调单元（如CPS4I 、C3D8Ｉ）的性价比很高.对于复杂模型，可以采用分割模型的方法划分二次四边形/六面体单元;有时分割过程过于繁琐，用户可以采用精度较高的二次三角形/四面体单元进行网格划分。

悬臂梁的线性静力学分析1。

1 问题的描述一悬臂梁左端受固定约束,右端自由,结构尺寸如图1—1所示,求梁受载后的Ｍises 应力、位移分布。

材料性质:弹性模量32e E =,泊松比3.0=ν均布载荷:Ｆ＝103N图1—1 悬臂梁受均布载荷图1.2 启动ＡB ＡQU Ｓ启动AB ＡＱUS 有两种方法,用户可以任选一种．（1）在Ｗin ｄow ｓ操作系统中单击“开始”—-“程序"——A ＢＡQU Ｓ 6.10-—AＢAQUS/ＣＡE。

（2）在操作系统的DOS窗口中输入命令:aｂaqｕs cａｅ。

启动ＡＢAQＵS／CAE后,在出现的Staｒt Sｅctioｎ（开始任务)对话框中选择Crｅate ModeｌDataｂａse。

1。

３创建部件在AＢAQUＳ／ＣAＥ顶部的环境栏中，可以看到模块列表：Module：Pａrt，这表示当前处在Part（部件)模块,在这个模块中可以定义模型各部分的几何形体。

悬臂梁的受力分析实验目的：学会使用有限元软件做简单的力学分析，加深对材料力学相关内容的理解，了解如何将理论与实践相结合。

实验原理：运用材料力学有关悬臂梁的的理论知识，求出在自由端部受力时，其挠度的大小，并与有限元软件计算相同模型的结果比较 实验步骤： 1，理论分析如下图所示悬臂梁，其端部的抗弯刚度为33EIl ，在其端部施加力F ，可得到其端部挠度为：33Fl EI ，设其是半径为0.05米，长为1米，弹性模量11210E =⨯圆截面钢梁，则其可求出理论挠度值3443Fl ERωπ=，先分别给F 赋值为100kN ，200kN ，300kN ，400kN ，500kN .计算结果如下表：F 100000 200000 300000 400000 500000 ω（m ）0. 033950. 0679060. 1018590. 13581230. 16976542有限元软件（ansys ）计算： （1）有限元模型如下图：模型说明,本模型采用beam188单元，共用11个节点分为10个单元，在最有段施加力为F计算得到端部的挠度如下表所示，F 100000 200000 300000 400000 500000S（端部位移）-0.34079E-01-0.680158E-01-1.020237E-01-1.360136E-01-1.700395E-01得到梁端部在收到力为100kN时Y方向的位移云图：将理论计算结果与ansys分析结果比较如下表：力F（N）100000 200000 300000 400000 500000 理论值0. 03395 0. 067906 0. 101859 0. 1358123 0. 1697654 实验值-0.34079E-01-0.680158E-01-1.020237E-01-1.360136E-01-1.700395E-01相对误差0.37% 0.16% 0.16% 0.15% 0.16%通过比较可得，理论值与软件模拟结果非常接近，在力学的学习中只要能熟练的掌握理论知识，在软件模拟过程中便可做到心中有数，在本实验中理论值是通过材料力学中得一些假设得到的一个解析解，而实验也是用了相同的假设，并将梁离散为十个单元，得到数值解，因此和理论值的误差是不可避免的，通过增加离散单元的个数可以有效的减少误差，但是增大了计算量，因此在实践中，只要选取合适的离散单元数，能够满足实践要求即可，这就需要有更加扎实有限元知识作为指导。

3）多箱单室（c、f）
4）多箱多室截面（e）
5）分离式箱形截面（g、h）
说明：悬臂部分（锚孔）——吊装时采用肋梁，悬臂施工时
采用箱梁；挂孔——一般采用肋梁，便于吊装
3、配筋特点：
纵向钢筋——悬臂上只承担负弯矩，配置负弯矩钢筋
——锚孔可能承担正或负弯矩需双向配筋
腹板——下弯的纵向钢筋，需要时布置竖向预应力钢筋
2 cos

tg 2
2h( R N y sin )
3 Re H ( 2h 3 ) N y cos ( 2h 3m )
（4）、专门空间分析
对于重要的牛腿应作为
专门课题来验算
返回
90
90
30.4
Lg
35
40
33
25
30
25
29
.2
悬臂主梁尺寸(m)
底缘曲线
H2
H1
三次曲线
11.0 3.2
10.0 2.5
8.5
7.5
2.0
2.0
ቤተ መጻሕፍቲ ባይዱ
园弧线
园弧线
10.1
9.2
园弧线
5.0
1.9
半立方抛
物线
5、牛腿构造特点
牛腿的高度不到悬臂梁高和挂梁梁高的一半，但要
传递较大的力——成为上部结构的薄弱部位，凹角处应
(3)双悬臂梁（或单悬臂梁）与简支挂梁联合组成多孔悬臂梁桥
多跨悬臂梁桥
(4)带挂梁的T形悬臂梁桥
多跨连续梁桥
T形刚构桥
其它特点：
（1）悬臂端容易下挠，行车舒适性较差。
（2）一般为静定结构，结构内力不受温度、混凝土收缩徐变
连续刚构桥

悬臂梁的有限元分析I. 内容综述悬臂梁的有限元分析是结构工程领域中的一个重要课题，它是一种数值计算方法，通过将连续的结构分解成许多小单元，然后对每个单元进行分析，最终得到整个结构的性能指标。

这种方法可以有效地模拟结构的变形和应力分布情况，为设计和优化提供可靠的依据。

在实际应用中，悬臂梁的有限元分析需要考虑多种因素，如材料属性、几何形状、载荷条件等。

因此在进行分析时，需要选择合适的模型和网格尺寸，并对边界条件进行合理设定。

此外由于悬臂梁的结构特点，其在不同位置的受力情况也有所不同，因此需要对各个部位进行分别分析。

悬臂梁的有限元分析是一项复杂而重要的工作，只有通过合理的建模和分析方法，才能得到准确的结果，并为实际工程提供有效的指导。

A. 研究背景和意义悬臂梁作为一种常见的结构形式，广泛应用于建筑、桥梁、机械等领域。

然而在实际应用过程中，由于各种因素的影响，悬臂梁的结构性能可能会发生退化，导致结构的安全性受到威胁。

因此对悬臂梁的有限元分析具有重要的研究意义。

有限元分析是一种基于数学模型的工程分析方法，通过将复杂的结构分解为若干个简单的单元，利用计算机模拟这些单元在受力作用下的变形和应力分布，从而预测结构的响应。

近年来随着计算机技术和数学方法的不断发展，有限元分析在工程领域中的应用越来越广泛，已经成为工程设计和施工的重要工具。

对于悬臂梁这种特殊结构，有限元分析不仅可以帮助我们了解其在不同工况下的性能表现，还可以为优化结构设计、提高结构强度和刚度提供理论依据。

此外通过对悬臂梁的有限元分析，我们还可以更好地了解其在使用过程中可能出现的缺陷和损伤，从而为预防事故、保障人员安全提供技术支持。

悬臂梁的有限元分析研究具有很高的实用价值和理论意义，对于推动工程技术的发展、提高人类生活质量具有重要作用。

B. 研究目的和方法本研究旨在通过有限元分析方法，对悬臂梁进行分析，以探究其在不同荷载下的应力分布情况。

我们将采用ANSYS软件进行模拟计算，并通过对计算结果的分析，得出悬臂梁的最大应力、最小应力以及平均应力等关键指标。

基于有限元法验证圣维南原理圣维南原理（Saint-Venant's principle）是结构力学的基本原理之一，用于描述原点附近一个点的剪力和弯矩与距离原点较远的地方施加的力和力矩之间的关系。

该原理可以通过有限元法进行验证。

有限元法是一种数值分析方法，广泛应用于工程领域。

它将结构划分为许多小的单元，通过计算每个单元的力和位移来近似求解整个结构的行为。

为验证圣维南原理，我们可以通过有限元法建立一个简化的结构模型。

假设我们有一个简单的悬臂梁，其长度为L、截面积为A、杨氏模量为E，并施加一个在距离原点处施加的力F。

首先，我们将梁划分为多个小单元，每个单元的长度为ΔL。

然后，我们根据材料的本构关系以及几何约束条件，建立结构的刚度矩阵和载荷向量。

对于每个单元，我们可以假设其形变是线性的，并利用梁的几何约束条件来推导出局部坐标系与全局坐标系之间的关系。

然后，利用局部坐标系中的应力-应变关系，我们可以得到每个单元的刚度矩阵。

接下来，我们将所有单元的刚度矩阵组装成整个结构的刚度矩阵，并将力向量组装为载荷向量。

根据位移与力的关系，我们可以通过求解线性方程组来得到结构的位移。

最后，我们可以利用得到的位移来计算结构上不同点的剪力和弯矩，并与理论解进行比较。

根据圣维南原理，当距离原点较远的地方施加的力和力矩趋于零时，该点的剪力和弯矩也会趋于零。

通过对模型的计算结果进行分析，我们可以验证圣维南原理。

如果模型中的剪力和弯矩在距离原点较远的地方确实趋于零，那么圣维南原理就得到了验证。

需要注意的是，由于有限元法是一种数值近似方法，验证结果可能会受到一些误差的影响。

因此，在进行验证时，我们需要合理选择模型的划分和参数，并进行适当的误差分析。

总结起来，通过建立一个简化的结构模型，并利用有限元法进行计算和分析，我们可以验证圣维南原理。

这种方法不仅可以验证圣维南原理，还可以用于研究和分析其他结构力学问题。

二维悬臂梁有限元分析二维悬臂梁有限元分析是一种常用的工程结构分析方法，在工程设计和研究中具有重要的应用价值。

本文将从有限元分析的原理和步骤、模型建立、载荷及边界条件、材料特性、求解方案以及结果分析等方面进行论述，探讨二维悬臂梁有限元分析的相关内容。

首先，有限元分析是一种通过将工程结构离散化为有限个小单元，利用单元的力学性质和相邻单元之间的相互作用关系，以数值解的方式求解结构的力学行为的方法。

二维悬臂梁有限元分析的步骤包括建立有限元模型、施加载荷和边界条件、确定材料特性、选择求解方案以及分析结果。

其次，模型建立是有限元分析的关键步骤之一、对于二维悬臂梁，可以采用梁单元进行建模。

梁单元是一种可以描述梁的位移、应变和应力的基本单元，具有两个节点和四个自由度。

通过将悬臂梁划分为多个梁单元，并将其节点连接起来建立悬臂梁有限元模型。

接下来，需要施加适当的载荷和边界条件。

载荷是指在悬臂梁上施加的外部力或力矩，可以是均布载荷、集中力、集中力矩等形式。

边界条件是指限制悬臂梁位移的条件，例如支座的固定或约束。

在二维悬臂梁中，通常将一端固定，即将该节点的两个位移约束为零。

选取合适的求解方案对于二维悬臂梁有限元分析非常关键。

常见的求解方案包括静态分析和动态分析。

静态分析适用于悬臂梁在静力加载下的弯曲和变形分析，动态分析适用于悬臂梁在动力加载下的响应分析。

根据具体问题的需求，选择适当的求解方案进行计算。

最后，需要对计算结果进行分析和评估。

通过数值计算得到的位移、应变和应力等结果，可以用于评估悬臂梁的强度和刚度等性能指标。

同时，也可以通过对结果的灵敏度分析，确定影响悬臂梁性能的关键因素，为工程设计提供参考。

综上所述，二维悬臂梁有限元分析是一种重要的工程结构分析方法。

通过有限元分析，可以预测悬臂梁的力学行为，为工程设计和结构优化提供依据。

然而，为了保证分析结果的准确性，需要合理地选择模型、载荷和边界条件、材料特性，以及采用适当的求解方案，对计算结果进行合理的解释和评估。

悬臂梁与悬链线悬臂梁和悬链线的受力分析与应用悬臂梁与悬链线的受力分析与应用悬臂梁是一种常见的结构形式，在工程中广泛应用。

它具有一个固定支点，另一端自由悬挂，承受着悬挂物体的重力或外力。

悬链线则是一种理想的支撑系统，以其受力特点被广泛运用于桥梁、建筑物等领域。

本文将对悬臂梁与悬链线的受力分析及其应用进行探讨。

一、悬臂梁的受力分析悬臂梁在受力分析时，常用到静力学的原理和方法。

在一般情况下，悬臂梁上的受力主要包括弯矩、剪力和轴向力。

1. 弯矩弯矩是悬臂梁上最常见的受力形态。

它产生的原因通常是悬挂物体的重力或外部载荷对悬臂梁产生的弯曲效应。

弯矩的大小与悬挂物体的重力、悬臂梁的长度、材料的弹性模量等因素密切相关。

为了确保悬臂梁的安全可靠，需要对弯矩进行准确的计算和结构设计。

2. 剪力剪力是悬臂梁上的另一种主要受力状态。

它是由于悬挂物体在悬臂梁上施加的垂直力所产生的反作用力。

剪力的大小与悬挂物体的重力、悬臂梁的长度、材料的弹性模量以及支点处的支撑能力等因素有关。

在实际工程中，需要对剪力进行准确的计算，以确保悬臂梁的结构安全。

3. 轴向力轴向力是悬臂梁上的受力形态之一，是指沿悬臂梁轴线方向的力，通常由悬挂物体和外部载荷引起。

轴向力的存在会对悬臂梁的稳定性和强度产生重要影响，因此需要进行合理的受力分析和结构设计。

二、悬链线的受力分析悬链线是一种理想的支撑系统，在桥梁、建筑物等工程中得到广泛应用。

它的特点是受力均匀分布于各个支点上，不会发生峰值应力集中的情况，因此具有较好的抗压和抗拉性能。

1. 支撑特性悬链线以其优良的支撑特性而被广泛使用。

在悬链线中，各个支点之间的受力均匀分布，不会出现局部受力过大的情况。

这种均匀分布的受力特点使得悬链线能够承受更大的压力和拉力，提高了结构的稳定性和强度。

2. 悬链线与悬臂梁的应用悬链线与悬臂梁经常结合应用于桥梁、吊车等工程中。

通过合理地结合悬链线的支撑特性和悬臂梁的受力分析，可以实现工程结构的稳定性和可靠性。

悬臂梁结构分析摘要：以某型自升式钻井平台的悬臂梁为例建立相应结构分析模型，给出了分析的载荷及边界条件，并对不同载荷条件下的计算结果进行了分析和评估，可作为此类结构设计的参考。

关键词：悬臂梁，结构分析.Abstract: to a certain type of jack-up drilling platform as an example of the cantilever beam establish corresponding structure analysis model, and gives out the analysis of load and boundary conditions, and under the conditions of different load calculation results are analyzed and evaluated, and can be used for this kind of structure design of the reference.Keywords: cantilever beam and structure analysis.正文：1 引言陆上可利用的资源和能源越来越少，许多国家都把开发利用海洋资源和能源作为国家战略[1]。

经过近几十年的高速发展，我国的能源问题日益严峻。

我国的海域辽阔，海上资源的开发潜力巨大，是未来我国能源可持续发展的重点[2~4]。

海上作业平台是进行海上资源开发的重要装备，目前我国在海上钻井平台的开发设计方面与技术先进国家尚有较大差距。

移动式海上平台在我国海上油气勘探开发中发挥着重要作用[5]，开展海上平台关键技术研究对保障我国能源安全和推动我国装备制造业的发展具有重要意义。

自升式钻井平台属于海上移动式平台，适宜于近浅海作业，是目前被广泛使用的海上钻井装备之一。

本文以某型自升式钻井平台的悬臂梁为例，对其进行结构分析和强度评估，为此类结构的设计提供参考方法。

悬臂梁实验一、实验目的1. 测定悬臂梁上下表面的应力，验证梁的弯曲理论二、实验仪器设备与工具1. 材料力学组合实验台中悬臂梁实验装置与部件2. A XL 2118系列静态电阻应变仪3. 游标卡尺、钢板尺三、实验原理与方法将试件固定在实验台架上，梁在纯弯曲时，同一截面上表面产生压应变，下表面产生拉应变，上下表面产生的拉压应变绝对值相等。

此时，可得到不同横截面的正应力σ，计算公式WM =σ 式中： M — 弯矩 L P M ⋅= （L —载荷作用点到测试点的距离）W — 抗弯截面矩量 62bh W =在梁的上下表面分别粘贴上应变片R 1，R 2；如图1所示，当对梁施加载荷P 时，梁产生弯曲变形，在梁内引起应力。

图1 悬臂梁受力简图及应变片粘贴图实验接线方式实验接桥采用1/4桥（半桥单臂）方式，应变片与应变仪组桥接线方法如图2所示。

使用试件上的应变片（即工作应变片1#、2#）分别连接到应变仪测点的A/B 上，测点上的B 和B1用短路片短接；温度补偿应变片连接到桥路选择端的A/D 上，桥路选择短接线将D1/D2短接，并将所有螺钉旋紧。

四、实验步骤1. 设计好本实验所需的各类数据表格。

图2 应变片与应变仪接线图2. 测量悬臂梁的有关尺寸，确定试件有关参数。

见附表13. 拟订加载方案。

选取适当的初载荷P 0，估算最大载P max (该实验载荷范围≤50N)，一般分4～6级加载。

4. 实验采用多点测量中半桥单臂公共补偿接线法。

将悬臂梁上两点应变片按序号接到电阻应变仪测试通道上，温度补偿片接电阻应变仪公共补偿端。

5. 按实验要求接好线，调整好仪器，检查整个测试系统是否处于正常工作状态。

6. 实验加载。

用均匀慢速加载至初载荷P 0。

记下各点应变片初读数，然后逐级加载，每增加一级载荷，依次记录各点应变仪的εi ，直至终载荷。

实验至少重复三次。

见附表27. 作完实验后，卸掉载荷，关闭电源，整理好所用仪器设备，清理实验现场，将所用仪器设备复原，实验资料交指导教师检查签字。