经济学原理 第八章 Slutsky方程

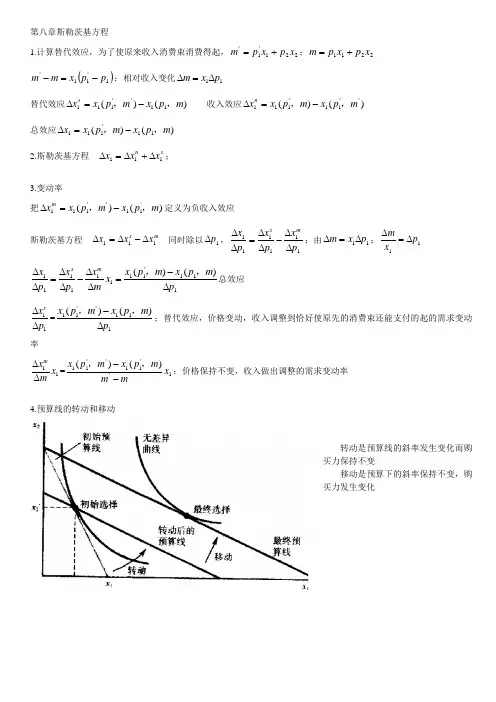
第八章斯勒茨基方程1.计算替代效应，为了使原来收入消费束消费得起，221'1'x p x p m +=；2211x p x p m +=()1'11'p p x m m -=-；相对收入变化11p x m ∆=∆替代效应)()(11''111m p x m p x x s ，，-=∆ 收入效应)()(''11'111m p x m p x x n ，，-=∆ 总效应)()(11'111m p x m p x x ，，-=∆ 2.斯勒茨基方程 s n x x x 111∆+∆=∆；3.变动率把)()('11''111m p x m p x x m，，-=∆定义为负收入效应斯勒茨基方程 m sxx x 111∆-∆=∆同时除以1p ∆，111111p x p x p x m s ∆∆-∆∆=∆∆；由11p x m ∆=∆；11p x m∆=∆ 111111x m x p x p x m s ∆∆-∆∆=∆∆111'11)()(p m p x m p x ∆-=，，总效应 11p x s ∆∆=111''11)()(p m p x m p x ∆-，，；替代效应，价格变动，收入调整到恰好使原先的消费束还能支付的起的需求变动率11x m x m∆∆=1''11''11)()(x mm m p x m p x --，，；价格保持不变，收入做出调整的需求变动率4.预算线的转动和移动转动是预算线的斜率发生变化而购买力保持不变移动是预算下的斜率保持不变，购买力发生变化5.希克斯的替代效应预算线不是绕着初始消费束转动，二是绕着穿过初始消费束的无差异曲线转动希克斯的替代效应是保持效用不变6.完全互补情况下的斯勒茨基分解替代效应为0收入效应就是总效应7.完全替代情况下的斯勒茨基分解收入效应为0，替代效应就是总效应8.拟线性偏好收入效应为0替代效应为总效应9.退税征税，价格由p 上升到t p p +='，消费数量由x 减少到'x 政府收入'')(x p p R -= 最初的预算约束为 m y px =+实行退税计划后的预算约束''')(tx m y x t p +=++()''y x ，在原来的预算约束上消费的起，消费者的效应变坏10.自愿实时定价气温上升实时价格上涨，削减电量，获得回购； 改善了用户的效用情况。

slutsky方程斯拉茨基方程（Slutsky equation）是经济学中的一种重要工具，用于分析需求的变化对价格、数量和收入的影响。

该方程是由瑟奈·斯拉茨基（Eugen Slutsky）于1915年首次提出。

斯拉茨基方程可以表示为：∆x=SE+IE其中，∆x表示需求量的变化，SE表示替代效应，IE表示收入效应。

替代效应可以通过边际替代率（marginal rate of substitution）来度量，边际替代率表示为消费者愿意放弃一种物品来增加另一种物品的程度。

当价格下降时，消费者更倾向于购买价格更低的物品，因此替代效应会导致需求量增加。

收入效应则通过边际效用（marginal utility）来度量，边际效用表示为消费者对一单位物品的额外满足程度。

当价格下降时，消费者的购买力增加，因此收入效应会导致需求量增加。

收入效应在正常商品（normal good）和劣质商品（inferior good）上会产生不同的影响。

斯拉茨基方程的应用范围十分广泛。

首先，它可以用于解释不同价格水平下的需求变化。

通过计算替代效应和收入效应的相对作用，我们可以更好地预测和解释市场行为。

其次，斯拉茨基方程还可以用于分析消费者行为的福利效应。

通过比较需求曲线的变化与边际效用曲线的变化，我们可以判断消费者的总体福利是增加还是减少。

此外，斯拉茨基方程还可以用于分析生产要素的需求弹性（elasticity of factor demand）。

通过将斯拉茨基方程应用于生产要素的市场，我们可以了解生产者对成本变化的反应程度。

总之，斯拉茨基方程是经济学中一种重要的工具，用于分析需求的变化对价格、数量和收入的影响。

通过将需求曲线拆分为替代效应和收入效应，我们可以更好地理解市场行为，预测和解释市场变动，并评估消费者的福利效应和生产要素需求的弹性。

slutsky方程
斯拉茨基方程是经济学中的一个重要概念，它是由俄罗斯经济
学家叶夫根尼·斯拉茨基（Evsey Domar）在20世纪20年代提出的。

斯拉茨基方程描述了一个经济体系中的总产出对价格和投入要素的
弹性关系。

斯拉茨基方程通常被用于分析生产函数和成本函数之间
的关系，以及在市场中生产者和消费者之间的相互作用。

斯拉茨基方程可以用数学公式表示为，Σ(p_i x_i) = Σ(p_i x_i^0) + Σ(p_i dx_i)，其中Σ代表求和符号，p_i代表价格，
x_i代表投入要素，dx_i代表投入要素的变化量。

这个方程可以帮
助经济学家分析在不同价格和投入要素变化的情况下，总产出的变
化情况。

从宏观经济学的角度来看，斯拉茨基方程可以帮助我们理解价
格水平对总产出的影响，以及投入要素的变化对经济增长的影响。

从微观经济学的角度来看，斯拉茨基方程可以帮助企业和生产者优
化其生产组合，以最大化产出并最小化成本。

斯拉茨基方程在实际应用中有着广泛的用途，例如在农业经济
学中用于分析农产品的供求关系，在产业经济学中用于分析不同产
业之间的竞争关系等。

总之，斯拉茨基方程作为经济学中的重要工具，对于理解经济体系的运行机制和优化资源配置具有重要意义。

slutsky方程
（原创实用版）
目录
1. Slutsky 方程的定义和背景
2. Slutsky 方程的应用领域
3. Slutsky 方程的优点和局限性
正文
Slutsky 方程是经济学中一种用于描述货币需求和货币供应之间关系的方程，由苏联经济学家 Slutsky 在 1937 年首次提出。

该方程主要描述了在特定经济环境下，货币需求与货币供应量、利率、价格水平等因素之间的关系。

Slutsky 方程的应用领域广泛，不仅包括了货币理论研究，也包括了货币政策制定和宏观经济分析等实际应用领域。

通过 Slutsky 方程，经济学家可以更好地理解货币需求和货币供应之间的关系，从而更准确地预测经济波动和通货膨胀等宏观经济现象。

然而，Slutsky 方程也有其优点和局限性。

首先，Slutsky 方程假设了许多理想的经济条件，例如完全竞争、完全信息等，这些假设在实际经济生活中并不总是成立。

其次，Slutsky 方程只考虑了货币需求和货币供应之间的关系，并未考虑到其他影响经济波动的因素，如财政政策、国际贸易等。

第1页共1页。