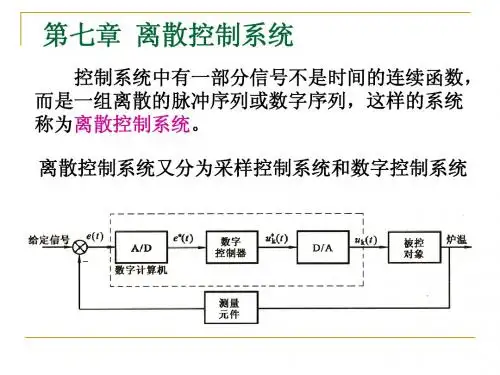
采样控制系统的分析1. 引言采样控制系统是现代自动控制系统中的一个重要组成部分。
它通过对被控对象进行采样和控制操作，实现对系统动态特性的精确控制。
本文将对采样控制系统进行深入分析，包括系统的基本原理、特点以及应用。
2. 采样控制系统的基本原理采样控制系统是基于采样周期的自动控制系统，其基本原理是通过周期性采样对被控对象的状态进行测量，并根据测量结果进行控制操作。
采样系统由采样器、控制器和执行器组成。
2.1 采样器采样器是采样控制系统中用于对被控对象进行采样的部件。
它包括传感器和采样信号处理器两部分。
传感器将被控对象的状态转换为电信号，而采样信号处理器则对传感器输出的信号进行采样和处理，获得被控对象在每个采样周期内的状态。
2.2 控制器控制器是采样控制系统中用于根据采样结果进行控制操作的部件。
它根据被控对象的状态和目标控制要求，计算并输出控制信号。
常见的控制器包括比例-积分-微分（PID）控制器、模糊控制器等。
2.3 执行器执行器是采样控制系统中用于执行控制操作的部件。
它接收控制信号并将其转换为对被控对象的操作，实现对被控对象状态的调节。
常见的执行器包括电动执行器、气动执行器等。
3. 采样控制系统的特点采样控制系统具有以下特点：3.1 时变性由于采样控制系统是周期性的，它对被控对象的控制是离散的。
这使得系统在不断变化的环境和外界干扰下，能够对被控对象的状态进行实时调节。
3.2 数字化采样控制系统使用数字技术对被控对象进行采样和控制，使得系统具有较高的精度和稳定性。
此外，数字化还使得系统易于实现自动化和远程控制。
3.3 离散性采样控制系统是离散系统，它通过周期性采样和控制操作来实现对被控对象的控制。
这种离散性使得系统具有一定的响应速度和抗干扰能力，但也会对系统的控制性能产生一定影响。
4. 采样控制系统的应用采样控制系统广泛应用于工业自动化、航空航天、电力系统等领域。
4.1 工业自动化在工业自动化中，采样控制系统用于对机械设备、生产线等进行控制。
