n 0
1 1 1 1 2 3 ....... z z z
上式是一个公比为 1 ,首项为 1 的几何级数 ,其和为: z 1 z E( z) . z 1 -1 1- z z -1
例7-5
求理想脉冲序列
T (t )
n 0
的z变换
e(t ) T (t ) (t nT )
E ( z)
1 z ( z 1 1) 1 z 1 z 1
e* (t )
从例7-4和例7-5可见,相同的z变换 E(z) 对应于相同的采样函数 ,但是不一定对应于相同的连续函数 e(t).
例7-6
求指数函数
e(t ) e-at
anT
的 z变换
解:
E( z) e
解: 因为 T 为采样周期,故
*
e (t ) T (t ) (t nT )
由拉氏变换知 因此
E * ( s ) e nsT
n 0
E ( z ) z n 1 z 1 z 2
的z变换为 (t )
T
n 0
n 0
把上式写成闭合形式.得
iii、z变换的收敛和特性
z变换定义为 E ( z ) e(nT ) z n
以z为自变量的罗朗级数。 收敛条件 z 1
n 0
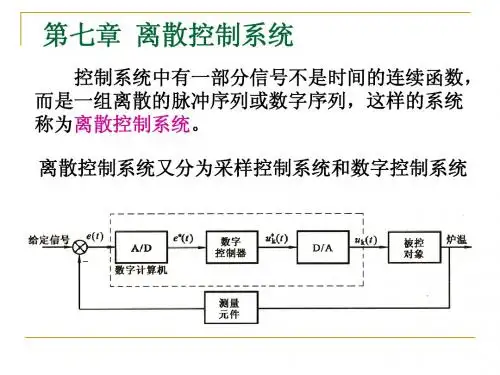
7.3.2
z 变换方法
⑴ 级数求和法(从定义出发) 例7-4 求单位阶跃函数的z变换
解 : 因为e(t ) 1(t ) 所以E ( z ) Z 1(t ) 1(nT ) z n
图7-9 零阶保持器的频率特 性 ③ 时间滞后特性.零阶保持器的输出为阶梯信号eh(t),其平均响应