北师大版数学七年级下册：《2.4 用尺规作角》习题

《用尺规作角》习题一、选择题1．下列关于作图的语句中正确的是（）A．画直线AB=10厘米B．画射线OB=10厘米C．已知A，B，C三点，过这三点画一条直线D．过直线AB外一点画一条直线和直线AB平行2．下列属于尺规作图的是（）A．用刻度尺和圆规作△ABC B．用量角器画一个300的角C．用圆规画半径2cm的圆 D．作一条线段等于已知线段3．尺规作图的画图工具是（）A．刻度尺、量角器B．三角板、量角器C．直尺、量角器 D．没有刻度的直尺和圆规4．下列作图语句正确的是（）A．以点O为顶点作∠AOB B．延长线段AB到C，使AC=BC C．作∠AOB，使∠AOB=∠αD．以A为圆心作弧5．图中的尺规作图是作（）A．线段的垂直平分线 B．一条线段等于已知线段C．一个角等于已知角 D．角的平分线6．下列作图语句正确的是（）A．作射线AB，使AB=a B．作∠AOB=∠aC．延长直线AB到点C，使AC=BC D．以点O为圆心作弧7．下列叙述中，正确的是（）A．以点O为圆心，以任意长为半径画弧，交线段OA于点B B．以∠AOB的边OB为一边作∠BOCC．以点O为圆心画弧，交射线OA于点BD．在线段AB的延长线上截取线段BC=AB8．下列尺规作图的语句错误的是（）A．作∠AOB，使∠AOB=3∠αB．作线段AB，使线段AB=aC．以点O为圆心画弧 D．作∠ABC，使∠ABC=∠α+∠β9．下列属于尺规作图的是（）A．用量角器画∠AOB的平分线OPB．利用两块三角板画15°的角C．用刻度尺测量后画线段AB=10cmD．在射线OP上截取OA=AB=BC=a10．下列关于作图的语句正确的是（）A．作∠AOB的平分线OE=3 cmB．画直线AB=线段CDC．用直尺作三角形的高是尺规作图D．已知A、B、C三点，过这三点不一定能画出一条直线11．下列作图属于尺规作图的是（）A．画线段MN=3cmB．用量角器画出∠AOB的平分线C．用三角尺作过点A垂直于直线L的直线D．已知∠α，用没有刻度的直尺和圆规作∠AOB，使∠AOB=2∠α12．下列尺规作图的语句错误的是（）A．作∠AOB，使∠AOB=3∠αB．以点O为圆心作弧C．以点A为圆心，线段a的长为半径作弧D．作∠ABC，使∠ABC=∠α+∠β二、填空题13．作图题的书写步骤是、、，而且要画出和，保留．14．下列语句表示的图形是（只填序号）①过点O的三条直线与另条一直线分别相交于点B、C、D三点：．②以直线AB上一点O为顶点，在直线AB的同侧画∠AOC和∠BOD：．③过O点的一条直线和以O为端点两条射线与另一条直线分别相交于点B、C、D三点：．15．下列语句是有关几何作图的叙述．①以O为圆心作弧；②延长射线AB到点C；③作∠AOB，使∠AOB=∠1；④作直线AB，使AB=a；⑤过三角形ABC的顶点C作它的对边AB的平行线．其中正确的有．（填序号即可）参考答案一、选择题1．答案：D解析：【解答】A、直线没有长度，故A选项错误；B、射线没有长度，故B选项错误；C、三点有可能在一条直线上，可画出一条直线，也可能不在一条直线上，此时可画出三条直线，故选项错误；D、正确．故选：D．【分析】根据基本作图的方法，逐项分析，从而得出正确的结论．2．答案：D解析：【解答】A、用刻度尺和圆规作△ABC，而尺规作图中的直尺是没有长度的，错误；B、量角器不在尺规作图的工具里，错误；C、画半径2cm的圆，需要知道长度，而尺规作图中的直尺是没有长度的，错误；D、正确．故选：D．【分析】根据尺规作图的定义分别分析得出即可．3．答案：D解析：【解答】尺规作图的画图工具是没有刻度的直尺和圆规．故选D．【分析】根据尺规作图的定义可知．4．答案：C解析：【解答】A、画角既需要顶点，还需要角度的大小，错误；B、延长线段AB到C，则AC＞BC，即AC=BC不可能，错误；C、作一个角等于已知角是常见的尺规作图，正确；D、画弧既需要圆心，还需要半径，缺少半径长，错误．故选C．【分析】根据画角的条件判断A；根据线段延长线的等腰判断B；根据基本作图判断C；根据确定弧的条件判断D．5．答案：A解析：【解答】根据图象是一条线段，它是以线段的两端点为圆心，作弧，进而作出垂直平分线，故做的是：线段的垂直平分线，故选：A．【分析】根据图象以及做线段垂直平分线的作法，即可得出答案．6．答案：B解析：【解答】A、射线是不可度量的，故选项错误；B、正确；C、直线是向两方无线延伸的，故选项错误；D、需要说明半径的长，故选项错误．故选B．【分析】根据射线、直线的延伸性以及确定弧的条件即可作出判断．7．答案：D解析：【解答】A、以点O为圆心，以任意长为半径画弧，交线段OA于点B，任意长为半径，不一定与线段AO相交，故此选项错误；B、以∠AOB的边OB为一边作∠BOC，∠BOC的度数不确定，故此选项错误；C、以点O为圆心画弧，交射线OA于点B，没有半径长，故此选项错误；D、在线段AB的延长线上截取线段BC=AB，正确．故选：D．【分析】分别利用尺规作图的定义，结合能否画出图形进而分析得出即可．8．答案：C解析：【解答】A、作一个角等于已知角的倍数是常见的尺规作图，语句正确；B、作一条线段等于已知线段是常见的尺规作图，语句正确；C、画弧既需要圆心，还需要半径，缺少半径长，这样的弧可以画出无数条，语句错误；D、作一个角等于两个已知角的和是基本作图，语句正确．故选C．【分析】分别利用尺规作图的定义，结合能否画出图形进而分析得出即可．9．答案：D解析：【解答】根据尺规作图的定义可得：在射线OP上截取OA=AB=BC=a，属于尺规作图，故选：D．【分析】根据尺规作图的定义：是指用没有刻度的直尺和圆规作图可直接选出答案．10．答案：D解析：【解答】A、作∠AOB的平分线OE=3 cm，角平分线是射线，故此选项错误；B、画直线AB=线段CD，直线没有长度，故此选项错误；C、用直尺作三角形的高是尺规作图，尺规应有圆规，故此选项错误；D、已知A、B、C三点，过这三点不一定能画出一条直线，此选项正确；故选：D．【分析】射线、直线具有延伸性，不能画出其长度；尺规作图需用圆规和无刻度的直尺；若A、B、C三点不共线，则无法过这三点画出一条直线，即A、B、C错误，D项正确．11．答案：D解析：【解答】A、画线段MN=3cm，需要知道长度，而尺规作图中的直尺是没有长度的，错误；B、用量角器画出∠AOB的平分线，量角器不在尺规作图的工具里，错误；C、用三角尺作过点A垂直于直线L的直线，三角尺也不在作图工具里，错误；D、正确．故选D．【分析】根据尺规作图的定义可知．12．答案：B解析：【解答】A、作一个角等于已知角的倍数是常见的尺规作图，正确；B、画弧既需要圆心，还需要半径，缺少半径长，错误．C、以点A为圆心，线段a的长为半径作弧，正确；D、作∠ABC，使∠ABC=∠α+∠β，正确故选B．【分析】根据基本作图的方法，逐项分析，从而得出结论．二、填空题13．答案：已知、求作、作法，图形，结论，作图痕迹．解析：【解答】作图题的书写步骤是已知、求作、作法，而且要画出图形和结论，保留作图痕迹．【分析】根据作图题的书写步骤和尺规作图的要求作答．14．答案：（3），（2），（1）．解析：【解答】①过点O的三条直线与另一条直线分别相交于点B、C、D三点的图形为（3）；②以直线AB上一点O为顶点，在直线AB的同侧画∠AOC和∠BOD的图形为（2）；③过O点的一条直线和以O为端点两条射线与另一条直线分别相交于点B、C、D三点的图形为（1）．【分析】图（1）为过点O有两条射线OC、OD，一条直线AB；图（2）为以直线AB上一点O 为顶点，在直线AB的同侧画∠AOC和∠BOD，图（3）为过点O的三条直线AB、OC、OD与另一条直线分别相交于点B、C、D三点．根据语句及图形特征进行选择．15．答案：③⑤．解析：【解答】①以O为圆心作弧可以画出无数条弧，因为半径不固定，所以叙述错误；②射线AB是由A向B向无限延伸，所以叙述错误；③根据作一个角等于已知角的作法，可以作一个角∠AOB，使∠AOB等于已知∠1，所以叙述正确；④直线可以向两方无限延伸，所以叙述错误；⑤根据平行公理：过直线外一点有且只有一条直线与已知直线平行，可以过三角形ABC的顶点C作它的对边AB的平行线，所以叙述正确．所以正确的有③⑤．【分析】①根据确定圆的两个条件：圆心和半径判断即可；②根据射线的性质判断即可；③根据基本作图：作一个角等于已知角判断即可；④根据直线的性质判断即可；⑤根据平行公理判断即可．。

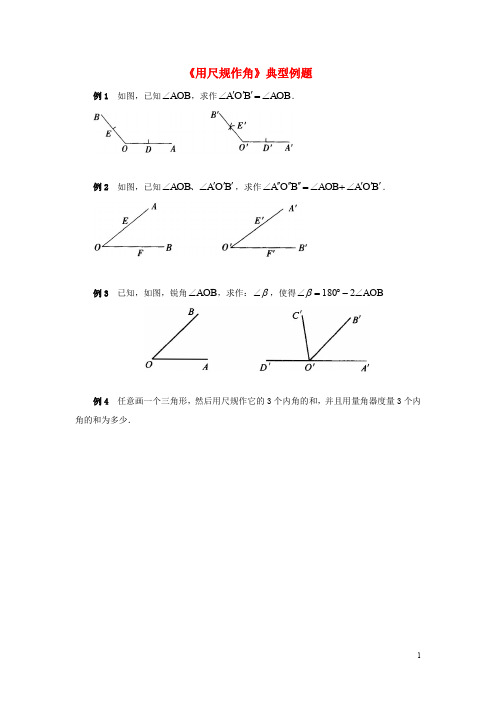
《用尺规作角》典型例题例1 如图，已知AOB ∠，求作AOB B O A ∠='''∠．例2 如图，已知B O A AOB '''∠∠、，求作B O A AOB B O A '''∠+∠=''''''∠．例3 已知，如图，锐角AOB ∠，求作：β∠，使得AOB ∠-︒=∠2180β例4 任意画一个三角形，然后用尺规作它的3个内角的和，并且用量角器度量3个内角的和为多少．参考答案例1 分析：要作AOB B O A ∠='''∠，可以先作A O ''，在此基础上我们再来确定B O ''的位置．作法：（1）作射线A O ''．（2）以O 为圆心，以任意长为半径画弧交OA 于D ，OB 于E ．（3）以O '为圆心，以OE 为半径画弧交A O ''于D ．（4）以D '为圆心，以DE 为半径画弧和前弧交于E '点．（5）过E '作射线B O ''，则B O A '''∠就是所要求的角．说明：在进行第2步时，以“任意长为半径”，要注意这个“任意”要适当，否则就都会给作图带来不必要的麻烦．例 2 分析：我们可以先作出一个角等于AOB ∠，再在这个角的外边，以这个角的一边为边作一个角等B O A '''∠，这就作出了这两个角的和，这个过程可以简化成如下过程．作法：（1）作射A O ''''．（2）以O 为圆心任意长为半径画弧交OA 于E ，OB 于F ；再以O '为圆心同样长为半径画弧交A O ''于E '，B O ''于F '．（3）以O ''为圆心，以OE 为半径画弧交A O ''''于E ''．（4）以E ''为圆心，以EF 为半径画弧，于前弧交于D 点；再以D 点为圆心，以F E ''为半径画弧，交E ''、D 所同在的弧为F ''点．（5）作射线F O ''''，则B O A ''''''∠就是所求的角．说明：中间连结D O ''这一步直接省略即可．例3 分析：首先作出AOB ∠2，再求AOB ∠2的补角即是所求的角．作法：1．作AOB B O A ∠='''∠，2．以B O ''为始边作AOB C O B ∠='''∠3．反向延长射线A O ''到D '．β∠为图中所示的D O C '''∠例4 分析：首先根据题目叙述写出已知、求作，然后再作图． 解：已知：如图，已知三角形ABC ．求作：DOG ∠，使C B A DOG ∠+∠+∠=∠．作法：（1）作A DOE ∠=∠；（2）以OE 为一边，在A DOE ∠=∠的外部作B EOF ∠=∠；（3）以OF 为一边，在EOF ∠的外部作C GOF ∠=∠． DOG ∠就是所求作的角（如图）．用量角器量得︒=∠180DOG ．。

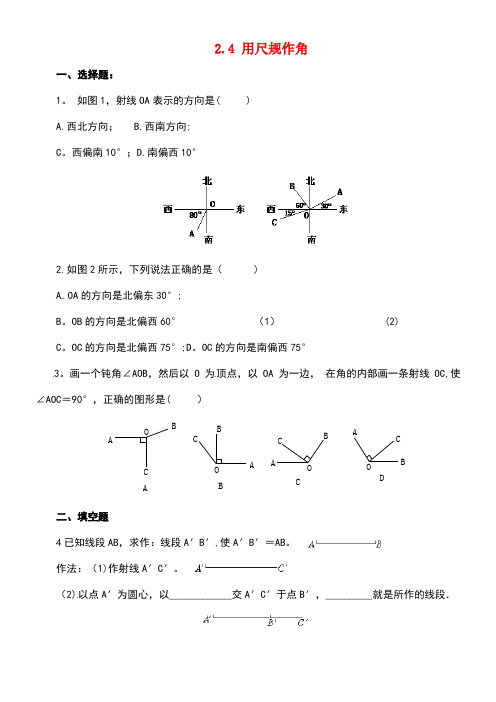
2.4 用尺规作角●教学目标(一)教学知识点1.会用尺规作一个角等于已知角.2.利用尺规作一个角等于已知角的应用.(二)能力训练要求会用尺规作一个角等于已知角，并了解它在尺规作图中的简单应用.(三)情感与价值观要求通过作图，进一步激发学生的学习兴趣，体验数学在生活中的应用.●教学重点用尺规作一个角等于已知角.●教学难点理解画图的语言，能根据几何语言画出图形.●教学方法讲练结合法●教具准备师：直尺、圆规.投影片一张第一张：引例(记作投影片§2.4 A)生：直尺、圆规、量角器●教学过程Ⅰ.创设现实情景，引入新课［师］在上节课我们学习了用直尺和圆规作图，并且引入了规范的尺规作图语言.从而能够用几何语言描述作一条线段等于已知线段.那么如何用尺规作一条线段等于已知线段呢？［生］已知线段a,求作：线段AB，使AB=a.作法：(1)作射线AC.(2)以点A为圆心，以a的长为半径画弧，交AC于点B.则，AB就是所求的线段.图2－64［师］很好.同学们已掌握了一些尺规作图的语言.下面大家看一实例，你能解决它吗？(出示投影片§2.4 A)如图2－65，要在长方形木板上截一个平行四边形，使它的一组对边在长方形木板的边缘上，另一组对边中的一条边为AB.(1)请过C点画出与AB平行的另一条边.(2)如果你只有一个圆规和一把没有刻度的直尺，你能解决这个问题吗？图2－65［师］大家讨论讨论.［生甲］要在长方形木板上截一个平行四边形，按上图的方式(平行四边形的一组对边在长方形木板的边缘上).只要保证过点C作出与AB平行的另一条线段即可.所以我用一个三角板的一边与AB重合，用直尺紧靠三角板的另一边，然后移动三角板，使与AB重合的那边过点C，这样过C点画线段CD，则CD 就是所求的与AB平行的另一边.如图2－66.图2－66［生乙］只有一个圆规和一把没有刻度的直尺，现在还不能解决这个问题.［生丙］过直线外一点作这条直线的平行线的原理是：同位角相等，两直线平行.所以，能不能过点C作一个角等于∠BAC，且使这两个角是同位角呢？［师］同学们讨论得很好，尤其是丙同学提出的问题：作一个角等于已知角.这节课，我们就来利用尺规作一个角等于已知角.Ⅱ．讲授新课［师］用尺规作图，它的步骤有哪些呢？［生］已知、求作、分析、作法.［师］好，那我们现在先来写已知、求作.［师生共析］已知：∠AOB,求作:∠A′O′B′,使∠A′O′B′=∠AOB.图2－67［师］这个∠A′O′B′如何就能作出呢？它的道理是什么呢？这将在第五章中谈到.现在我们只需按下列作法步骤去画即可.下面老师在黑板上画、叙述，同学们在下面用尺规作∠A′O′B′,使∠A′O′B′=∠AOB.作法：(1)作射线O′A′.(2)以点O为圆心，以任意长为半径画弧，交OA于点C，交OB于点D.(3)以点O′为圆心，以OC长为半径画弧，交O′A′于点C′.(4)以点C′为圆心，以CD长为半径画弧，交前面的弧于点D′.(5)过点D′作射线O′B′.∠A′O′B′就是所求作的角.图2－68［师］同学们作好了没有？［生齐声］好了.［师］那你所作的角一定等于已知角吗？……［师］大家来比较一下.［生甲］我用量角器量了量所作的角与已知角，可以知道这两个角相等.［生乙］我把所作的角与已知角重叠，看到这两个角的终边与始边重合，说明所作的角与已知角相等.［师］很好.这样我们就会用尺规作一个角等于已知角.下面我们两人一组，再作一个角等于已知角，一人叙述作法，一人根据作图.……［师］大家基本掌握了用尺规作一个角等于已知角.接下来我们通过练习进一步熟悉掌握这内容.Ⅲ.课堂练习(一)课本随堂练习1.已知∠AOB,利用尺规作∠A′O′B′，使∠A′O′B′=2∠AOB.图2－69 图2－70作法：(1)以O为圆心，以任意长为半径画弧，与OA交于点A′，与OB交于点C.(2)以点C为圆心，以A′C长为半径画弧，交前弧于点B′.(3)过点B′作射线OB′，则∠A′OB′就是所求作的角.或者：作法：(1)作射线O′A′.(2)以O点为圆心，以任意长为半径画弧交OA于点C，交OB于点D.图2－71 图2－72(3)以点O ′为圆心，以OC 长为半径画弧，交O ′A ′于C ′点.(4)以点C ′为圆心，以CD 长为半径画弧，交前弧于E 点.(5)以点E 为圆心，以CD 长为半径画弧，交于点B ′.(6)过点B ′作射线OB ′.则∠A ′O ′B ′就是所求作的角.2.利用尺规完成本节课开始时提出的问题.作法：(略)，图如下图2－73(二)看书 “读一读”.Ⅳ.课时小结本节课我们主要学习了用尺规作一个角等于已知角.要会用自己的语言来书写作法，并要了解作一个角等于已知角在尺规作图中的简单应用.Ⅴ.课后作业(一)课本P 57习题2.7 1.(二)复习本章的全部内容，并作一小结.Ⅵ.活动与探究1.利用尺规设计一些美丽的图案.［过程］通过这个活动，一方面使学生进一步掌握尺规作图的方法，另一方面也可培养学生的动手、动脑能力，激发他们的创造力，增进其对数学的理解.［结果］结果是许多学生设计出好多的美丽图案.C ′E●板书设计§2.4 用尺规作角一、做一做：作一个角等于已知角已知求作作法二、课堂练习三、读一读四、课时小结五、课后作业。

用尺规作角课后作业一、选择题1、尺规的作图是指（）A. 用直尺规范作图B. 用刻度尺和圆规作图C. 用没有刻度的直尺和圆规作图D. 直尺和圆规是作图工具2、下列关于作图的语句中正确的是（）A. 画直线AB=10厘米B. 画射线OB=10厘米C. 已知A，B，C三点，过这三点画一条直线D. 过直线AB外一点画一条直线和直线AB平行3、如图，给出了过直线外一点作已知直线的平行线的方法，其依据是（）A. 同位角相等，两直线平行B. 内错角相等，两直线平行C. 同旁内角互补，两直线平行D. 两直线平行，同位角相等4、如图，用尺规作出∠OBF=∠AOB，作图痕迹⌒MN是（）A. 以点B为圆心，OD为半径的圆B. 以点B为圆心，DC为半径的圆C. 以点E为圆心，OD为半径的圆D. 以点E为圆心，DC为半径的圆5、如图，点C在∠AOB的OB边上，用尺规作出了CN∥OA，作图痕迹中，⌒FG是（）A. 以点C为圆心，OD为半径的弧B. 以点C为圆心，DM为半径的弧C. 以点E为圆心，OD为半径的弧D. 以点E为圆心，DM为半径的弧二、填空题6、如图，已知方格纸中的每个小方格都是相同的正方形．∠ACB画在方格纸上，请在小方格的顶点上标出一个点P，使点P落在∠ACB的平分线上．．7、如图所示，已知∠AOB，求作射线OC，使OC平分∠AOB，作法的合理顺序是．（将①②③重新排列）①作射线OC；②以O为圆心，任意长为半径画弧交OA、OB于D、E；③分别以D、E为圆心，大于12DE的长为半径作弧，在∠AOB内，两弧交于点C．8、画线段AB；延长线段AB到点C，使BC=2AB；反向延长AB到点D，使AD=AC，则线段CD= AB．9、已知∠AOB，点P在O A上，请以P为顶点，PA为一边作∠APC=∠O（不写作法，但必须保留作图痕迹）问：PC与OB一定平行吗？答：．10、如图已知∠AOB内有两点，M、N求作一点P，使点P在∠AOB两边距离相等，且到点M、N的距离也相等，保留作图痕迹并完成填空．解：（1）连接；作垂直平分线CD；（2）作∠AOB的OE与CD交于点，所以点就是要找的点．三、解答题11、如图，在方格纸上：（1）已有的四条线段中，哪些是互相平行的？（2）过点M画AB的平行线．（3）过点N画GH的平行线．12、如图，已知∠α，∠β，用直尺和圆规求作一个∠γ，使得∠γ=∠α-12∠β．（只须作出正确图形，保留作图痕迹，不必写出作法）参考答案1．解析：根据尺规作图的定义可知：尺规作图是指用没有刻度的直尺和圆规作图．故选C．2．解析：A、直线没有长度，错误；B、射线没有长度，错误；C、三点有可能在一条直线上，可画出一条直线，也可能不在一条直线上，此时可画出三条直线，错误；D、正确．故选D．3．解析：图中所示过直线外一点作已知直线的平行线，则利用了同位角相等，两直线平行的判定方法．故选A．4．解析：作∠OBF=∠AOB的作法，由图可知，①以点O为圆心，以任意长为半径画圆，分别交射线OA、OB分别为点C，D；②以点B为圆心，以OC为半径画圆，分别交射线BO、MB分别为点E，F；③以点E为圆心，以CD为半径画圆，交⌒EF于点N，连接B N即可得出∠OBF，则∠OBF=∠AOB．故选D．5．解析：根据题意，所作出的是∠BCN=∠AOB，根据作一个角等于已知角的作法，⌒FG是以点E为圆心，DM为半径的弧．故选D．6．解析：作法：7．解析：作法：（1）以O为圆心，任意长为半径画弧交OA、OB于D、E；（2）分别以D、E为圆心，大于12DE的长为半径作弧，在∠AOB内，两弧交于点C，（3）作射线OC，所以OC就是所求作的∠AOB的平分线．故题中的作法应重新排列为：②③①．故答案为：②③①．8．解析：（1）画线段AB；（2）延长线段AB到点C，使BC=2AB；（3）反向延长AB到点D，使AD=AC；由图可知，BC=2AB，AD=AC=3AB，故CD=6AB．9．解析：作图如下：PC与OB一定平行．故答案是：平行．10．解析：如图，故答案为：（1）MN，MN，（2）角平分线，P，P．11．解析：（1）由图形可得：AB∥CD．（2）（3）所画图形如下：12．解析：作图如下，∠BCD即为所求作的∠γ．。

《2.4 用尺规作角》习题
1. 已知底边及一腰，求作等腰三角形.
2.已知：线段a，b，求作ΔABC，使∠BAC＝90°，BC＝a，AC＝b.
3.如图，已知在ΔABC中，∠A＝90°，请用圆规和直尺作⊙P，使圆心P在AC上，且与AB、BC两边都相切.
4.用圆规、直尺（三角尺）作图，不写作法，但要保留作图痕迹.如图，AB、CD是两条互相垂直的公路，设计时想在拐弯处用一段圆弧形弯道把它们连接起来（圆弧在A、C两点处分别与道路相切），测得AC＝60米，∠ACP＝45°.
（1）在图中画出圆弧形弯道的示意图；
（2）求弯道部分的长.（结果保留两个有效数字）.
5. 如图，ΔABC是某村若干亩土地的示意图，在党的“十六大”精神的指导下，为进一步加大农村经济结构调整的力度，某村决定把这块土地平均分给四位“花农”种植，请你帮他们分一分，提供两种分法.要求：画出图形，并简要说明分法.
第一种分法：第二种分法：
A A
B C B C
6.如图，某汽车探险队要从A城穿越沙漠去B城，途中需要到河流L边为汽车加水，汽车在河边哪一点加水，才能使行驶的总路程最短？请你在图上画出这一点.。

七年级数学下册第二章《尺规作图》专项练习班级：_________________ 姓名：_________________ 座号：________________ 评分:一. 选择题 (共10小题，答案写在表格内，否则答案无效)A ．刻度尺和圆规B ．不带刻度的直尺和圆规C ．刻度尺D ．圆规2．如图，用尺规作出∠OBF=∠AOB，作图痕迹MN 是（ ）．A ．以点B 为圆心，OD 为半径的圆 B ．以点B 为圆心，DC 为半径的圆 C ．以点E 为圆心，OD 为半径的圆D ．以点E 为圆心，DC 为半径的圆3．我们利用尺规作图可以作一个角()''A O B ∠等于已知角()AOB ∠，如下所示：（1）作射线OA ；（2）以O 为圆心，任意长为半径作弧，交OA 于C ，交OB 于D ； （3）以O '为圆心，OC 为半径作弧，交OA '于'C ； （4）以C '为圆心，OC 为半径作弧，交前面的弧于D ； （5）连接'O D '作射线,O B ''则A O B '''∠就是所求作的角． 以上作法中，错误的一步是（ ） A ．()2B ．()3C ．()4D ．()54．下面出示的的尺规作图题，题中符号代表的内容正确的是（ ） 如图，已知∠AOB ，求作：∠DEF ，使∠DEF =∠AOB作法：（1）以①为圆心，任意长为半径画弧，分别交OA 、OB 于点P 、Q ； （2）作射线EG ，并以点E 为圆心②长为半径画弧交EG 于点D ； （3）以点D 为圆心③长为半径画弧交（2）步中所画弧于点F ； （4）作④，∠DEF 即为所求作的角．A ．①表示点EB ．②表示PQC ．③表示OQD ．④表示射线EF5．用直尺和圆规作∠HDG＝∠AOB 的过程中，弧②是（ ）A ．以D 为圆心，以DN 为半径画弧B ．以M 为圆心，以DN 长为半径画弧C ．以M 为圆心，以EF 为半径画弧D ．以D 为圆心，以EF 长为半径画弧6．如图，是用直尺和圆规作一个角等于己知角的方法，即作'''A O B AOB ∠=∠．这种作法依据的是（ ）A ．SSSB ．SASC ．AASD ．ASA7．用直尺和圆规作∠HDG ＝∠AOB 的过程，弧①是（ ）A ．以D 为圆心，以DN 为半径画弧B ．以D 为圆心，以EF 为半径画弧C ．以M 为圆心，以DN 为半径画弧D ．以M 为圆心，以EF 为半径画弧8．下面是黑板上出示的尺规作图题，需要回答横线上符号代表的内容：如图，已知AOB ∠，求作：DEF ∠，使DEF AOB ∠=∠．作法：（1）以为圆心，任意长为半径画弧，分别交OA 、OB 于点P 、Q ；（2）作射线EG ，并以点E 为圆心，长为半径画弧交EG 于点D ；（3）以点D 为圆心，长为半径画弧交（2）步中所画弧于点F ；（4）作，DEF ∠即为所求作的角．A ．表示点EB ．表示PQC ．表示OQD ．表示射线EF9．如图，点C 在AOB ∠的OB 边上，用尺规作出了BCD AOB ∠=∠.以下是排乱的作图过程：①以C 为圆心，OE 长为半径画MN ，交OB 于点M . ②作射线CD ，则BCD AOB ∠=∠.③以M 为圆心，EF 长为半径画弧，交MN 于点D .④以O 为圆心，任意长为半径画EF ，分别交OA ，OB 于点E ，F .则正确的作图顺序是（ ）A ．①—②—③—④B ．③—②—④—①C ．④—①—③—②D ．④—③—①—② 10．在△ABC 中，AB=AC ，∠A=80°，进行如下操作：①以点B 为圆心，以小于AB 长为半径作弧，分别交BA 、BC 于点E 、F ； ②分别以E 、F 为圆心，以大于12EF 长为半径作弧，两弧交于点M ；③作射线BM 交AC 于点D ， 则∠BDC 的度数为（ ）.A ．100°B ．65°C ．75°D ．105°二．填空题（共7小题）11．在几何里，把只用_________和_________画图的方法称为尺规作图. 12．已知1∠和2∠，画一个角使它等于12∠+∠，画法如下： （1）画AOB ∠=______________．（2）以点O 为顶点，OB 为始边，在AOB ∠的__________作2BOC ∠=∠；则12AOC ∠=∠+∠．13．如图，∠CAD 为△ABC 的外角，按以下步骤作图：①以点B 为圆心，以适当长为半径画弧，交BA 于点M ，交BC 于点N ； ②以点A 为圆心，以BM 长为半径画弧，交AD 于点P ； ③以点P 为圆心，以MN 长为半径画弧，交前一条弧于点Q ； ④经过点Q 画射线AE ，若∠C＝50°，则∠EAC 的大小是_____度．14．下列作图中：①用量角器画出90AOB ∠=︒；②作AOB ∠，使2AOB α∠=∠；③连接AB ；④用直尺和三角板作AB 的平行线CD ，属于尺规作图的是__________．（填序号）15．已知∠α和线段m ，n ，求作△ABC ，使BC ＝m ，AB ＝n ，∠ABC ＝∠α，作法的合理顺序为________．(填序号即可)①在射线BD 上截取线段BA ＝n ；②作一条线段BC ＝m ；③以B 为顶点，以BC 为一边，作∠DBC ＝∠α；④连接AC ，△ABC 就是所求作的三角形．16．如图，CAD ∠为ABC ∆的外角，按以下步骤作图：①以点B 为圆心，以适当长为半径画弧，交BA 于点M ，交BC 于点N ；②以点A 为圆心，以BM 长为半径画弧，交AD 于点P ；③以点P 为圆心，以MN 长为半径画弧，交前一条弧于点Q ；④经过点Q 画射线AE ．若50C ∠=︒，则EAC ∠的大小是__________度．17．如图，在△ABC，∠C=90°，∠ABC=40°，按以下步骤作图：①以点A 为圆心，小于AC 的长为半径．画弧，分别交AB 、AC 于点E 、F ； ②分别以点E 、F 为圆心，大于12EF 的长为半径画弧，两弧相交于点G ； ③作射线AG ，交BC 边于点D ，则∠ADC 的度数为_____．三．解答题18．如图，在△ABC 中，BD 是边AC 上的高．请用尺规作图法，在BD 上求作一点E ，使得∠CED +∠ABD ＝90°．（保留作图痕迹，不写作法）19．已知：线段c 和αβ∠∠，求作：ABC ，使得AB c A B αβ=∠=∠∠=∠，，（不写作法，但保留作图痕迹）20．已知线段a 及锐角α，用直尺和圆规作ABC ，使B α∠=∠，AB BC a ==．21．尺规作图：已知α∠，β∠，求一个角∠AOB ，使∠AOB =α∠+β∠．（保留作图痕迹）22．如图，已知三角形ABC 和射线EM ，用直尺和圆规按下列步骤作图（保留作图痕迹，不写作法）：（1）在射线EM 的上方，作NEM B ∠=∠；（2）在射线EN 上作线段DE ，在射线EM 上作线段EF ，使得DE AB =，EF BC =；（3）连接DF ，观察并猜想：DF 与AC 的数量关系是DF ______AC ，填（“＞”、“＜”或“＝”） 23．按要求作图（1）如图，已知线段,a b ，用尺规做一条线段，使它等于+a b （不要求写作法，只保留作图痕迹）（2）已知：∠α，求作∠AOB=∠α（要求：直尺和圆规作图，不写作法，保留作图痕迹）24．如图，已知ABC 中，AB AC =，点P 在BC 上．（1）试用直尺和圆规在AC 上找一点D ，使CPD BAP ∠=∠（不写作法，但需保留作图痕迹）；（2）在（1）的条件下，若2APC ABC ∠=∠；求证：//PD AB ．25．（1）如图，在直线MN 的异侧有A 、B 两点，按要求画图，并注明画图的依据． 请在图1中直线MN 上画一点D ，使线段AD +BD 最短．依据是 ． （2）如图2，已知∠AOB，用圆规和没有刻度的直尺求作∠A'O'B',使∠A'O'B'=∠AOB26．如图，已知锐角△ABC ，点D 是AB 边上的一定点，请用尺规在AC 边上求作一点E ，使∠ADE =∠ABC ，（保留作图痕迹，不写做法）27．如图，已知α∠，β∠．求作：AOB ∠，使AOB αβ∠=∠-∠．（尺规作图，保留作图痕迹，不写作法）28．尺规作图（1）如图所示，已知线段AB ，∠α，∠β，用尺规作一个△ABC，使它的两个角分别为∠CAB=∠α，∠CBA=∠β．（不写作法，保留作图痕迹,图作在空白处）（2）已知：点P 为∠CAB 边上的一点，求作：直线PQ ，使得PQ∥AB29．如图，已知AOB ∠和射线O A ''．（1） 请用尺规作图法，在射线O A ''上作A O B '''∠，使得A O B AOB '''∠=∠； (不要求写作法，保留作图痕迹)．（2） 若40AOB ︒∠=，求AOB ∠的余角和补角．30．如图，已知点P 为∠AOB 一边OB 上的一点．（1）请利用尺规在∠AOB 内部作∠BPQ ，使∠BPQ ＝∠AOB ；（不写作法，保留作图痕迹）（2）根据上面的作图，判断PQ 与OA 是否平行？若平行，请说明理由．31．如图，在△ABC 中，∠C >∠B．（1）请用尺规过点C 作一条射线，与边AB 交于点D ，使△ACD ∽△ABC (保留作图痕迹，不写作法)；（2）已知AB ＝6，AC ＝4，求AD 的长． 32．作图与计算（1）已知：AOB α∠∠，．求作：在图2中，以OA 为一边，在∠AOB 的内部作．∠AOC ＝α∠（要求：直尺和圆规作图，不写作法，保留图痕迹．）（2）过点O 分别引射线OA 、OB 、OC ，且∠AOB =65°，∠BOC =30°，求∠AOC 的度数．33．如图，一块大的三角板ABC ，D 是AB 上一点，现要求过点D 割出一块小的三角板ADE ，使∠ADE=∠ABC，（1）尺规作出∠ADE．（不写作法，保留作图痕迹，要写结论） （2）判断BC 与DE 是否平行，如果是，请证明．34．如图，点D 在ABC △的AB 边上，且ACD A ∠=∠． （1）作BDC ∠的平分线DE ，交BC 于点E （用量角器画）．（2）在（1）的条件下，BDC ACD A ∠=∠+∠，判断直线DE 与直线AC 的位置关系．35．如图，已知△ABC，（1）作图：试过点C 作直线CD∥AB，（用尺规作图法，保留作图痕迹，不要求写作法）； （2）请你写出（1）的作图依据: .参考答案一. 选择题(每小题3分，共10小题)二．填空题（每小题4分，共7小题）11. 没有刻度的直尺圆规12. ∠1, 外部13. 50 14. ②③15. ②③①④ 16. 50 17. 65°三．解答题（共8小题）18.解：如图，点E为所求．19. 解：△ABC为所求作．20. 解：如图所示：△ABC即为所作．21. 解：如图，AOB ∠即为所作．22. 解：（1）如图所示：作法：①以点B 为圆心任意长为半径画圆弧，交AB ，BC 于点G ，H ②再以点E 为圆心以①中的半径画圆弧，交EM 于点P③再以点P 为圆心GH 长为半径画圆弧，与②所画的圆弧交于点N ，连接EN 即可 （2）如图所示：作法：①用圆规取BC 的长度，以点E 为圆心BC 长为半径画弧，交EM 于点F ，则EF=BC ②用圆规取AB 的长度，以点E 为圆心AB 长为半径画弧，交EN 的延长线于点D ，则DE=AB（3）根据EF=BC ，DE=AB ，B NEM ∠=∠可证ABC EDF △≌△，则DF=AC23. 解：（1）作射线CF ，在射线上顺次截取CD=a ，DE=b ，如下图所示，线段CE 即为所求：（2）首先作射线OA ，如下图所示，∠AOB 即为所求：24. 解：解：（1）如图所示．（2）∵2APC APD DPC ABC BAP ABC ∠=∠+∠=∠+∠=∠∴BAP ABC ∠=∠∵BAP CPD ∠=∠∴CPD ABC ∠=∠∴//PD AB ．25. 解：（1）D 点为线段AB 与直线MN 的交点，如图．依据为两点之间线段最短．（2）①作任意一射线O A ''，如图2；②以O 点为圆心，任意长度为半径作弧交OA 、OB 于点M 、N ，如图1；③以O '点为圆心，同样的长度为半径作弧交O A ''于点M '，如图2；④以点M '为圆心，MN 为半径作弧交③的弧于点N '，如图2；⑤连接O N ''并延长至B '，如图2，则A O B '''∠即为所求的角．26. 解：解：如图所示：通过这个方法作图，可以证明()BGF DAH SSS ≅，就可以得到ADE ABC =∠∠．27. 解：作∠AOC=α∠，然后在∠AOC 内部作∠BOC=β∠，即可得到AOB αβ∠=∠-∠，如下图所示，∠AOB 即为所求．28. 解：（1）如图所示：；（2）如图所示：．29. 解：（1）所作图形如答图2所示，A O B '''∠即为所求.（2） 当40AOB ∠=︒时，AOB ∠的余角=904050︒-︒=︒．AOB ∠的补角18040140=-=︒︒︒．30. 解：（1）如图所示： ；（2）BPQ AOB ∠=∠，//PQ OA ∴（同位角相等，两直线平行）．31. 解：（1）如图，CM 即为所求作的射线；（2）在△ABC和△ACD中，∵∠ACD=∠B，∠A=∠A，∴△ABC∽△ACD，∴AB AC AC AD=，∴224863ACADAB===．32. 解：（1）如图所示：∠AOC就是所求的角．（2）分两种情况讨论：①当OC在∠AOB内部时，如图1，∠AOC=∠AOB-∠BOC=65°-30°=35°；②当OC在∠AOB外部时，如图2，∠AOC=∠AOB+∠BOC=65°+30°=95°．33. 解：（1）如图，∠ADE为所作；（2）BC∥DE．理由如下：∵∠ADE=∠ABC，∴BC∥DE．34. 解：（1）如图：（2）DE∥AC，理由：∵∠BDC=∠A+∠DCA，∠A=∠DCA，∴∠BDC=2∠DCA，∵DE平分∠BDC，∴∠BDC=2∠EDC，∴∠EDC=∠DCA，∴DE∥AC.35. 解：(1)(2)同位角相等，两直线平行.。

2.4 用尺规作图同步测试一、单选题（共10题；共20分）1.如图所示的尺规作图的痕迹表示的是（）A. 尺规作线段的垂直平分线B. 尺规作一条线段等于已知线段C. 尺规作一个角等于已知角D. 尺规作角的平分线2.下列尺规作图的语句正确的是（）A. 延长射线AB到DB. 以点D为圆心，任意长为半径画弧C. 作直线AB=3cmD. 延长线段AB至C，使AC=BC3.已知三边作三角形，用到的基本作图是（）A. 作一个角等于已知角 B.平分一个已知角C. 在射线上截取一线段等于已知线段D. 作一条直线的垂线4.在直线m上顺次取A，B，C三点，使AB=10cm，BC=4cm，如果点O是线段AC的中点，则线段OB的长为（）A. 3cmB. 7cmC. 3cm或7cm D. 5cm或2cm5.用直尺和圆规作线段的垂直平分线，下列作法正确的是（）A. B. C.D.6.作已知角的平分线是根据三角形的全等判定（）作的．A. AASB. ASAC. SASD. SSS7.作一个角等于已知角用到下面选项的哪个基本事实（）A. SSSB. SASC. ASAD. AAS8.如图，用尺规法作∠DEC=∠BAC，作图痕迹的正确画法是（）A. 以点E为圆心，线段AP为半径的弧B. 以点E为圆心，线段QP为半径的弧C. 以点G为圆心，线段AP为半径的弧D. 以点G为圆心，线段QP为半径的弧9.在△ABC中，AB=AC，∠A=80°，进行如下操作：①以点B为圆心，以小于AB长为半径作弧，分别交BA、BC于点E、F；②分别以E、F为圆心，以大于EF长为半径作弧，两弧交于点M；③作射线BM交AC于点D，则∠BDC的度数为（）A. 100°B. 65°C. 75°D. 105°10.如图，在△ABC中，∠C=90°，以A为圆心，任意长为半径画弧分别交AB、AC于点M和N，再分别以M、N为圆心，大于MN的长为半径画弧，两弧交于点P，连结AP并延长交BC于点D，则下列说法错误的是（）A. ∠BAD=∠CADB. 点D到AB边的距离就等于线段CD的长C. S△ABD=S△ACDD. AD垂直平分MN二、填空题（共5题；共5分）11.如图，已知线段AB，分别以点A，B为圆心，大于线段AB长度一半的长为半径画弧，相交于点C，D，连接AC，BC，BD，CD．其中AB=4，CD=5，则四边形ABCD的面积为________ ．12.在△ABC中，按以下步骤作图：①分别以B，C为圆心，以大于BC的长为半径作弧，两弧相交于M，N两点；②作直线MN交AB于点D，连接CD，若CD=AC，∠B=25°，则∠ACB的度数为________ ．13.如图，用直尺和圆规画∠AOB的平分线OE，其理论依据是________ ．14.利用直尺和圆规作出一个角的角平分线的作法，其理论依据是全等三角形判定方法________ ．15.数学活动课上，同学们围绕作图问题：“如图，已知直线l和l外一点P，用直尺和圆规作直线PQ，使PQ⊥l于点Q．”其中一位同学作出了如图所示的图形．你认为他的作法的理由有________三、解答题（共2题；共20分）16.综合题。

北师大版七年级数学下册《2.4 用尺规作角》教案一. 教材分析《2.4 用尺规作角》这一节主要让学生掌握用尺规作角的方法和技巧。

通过这一节的学习，学生能够了解尺规作角的原理，并能够运用尺规作任意大小的角。

教材通过具体的操作实例，引导学生探究用尺规作角的方法，培养学生的动手能力和观察能力。

二. 学情分析学生在学习这一节之前，已经学习了用直尺和圆规画线段、圆的基本知识。

但是，对于用尺规作角的方法和技巧，可能还比较陌生。

因此，在教学过程中，需要引导学生通过实际的操作，掌握用尺规作角的方法。

三. 教学目标1.了解尺规作角的原理，掌握用尺规作角的方法和技巧。

2.能够运用尺规作出任意大小的角。

3.培养学生的动手能力和观察能力。

四. 教学重难点1.尺规作角的原理的理解。

2.用尺规作角的方法和技巧的掌握。

五. 教学方法采用“问题引导法”和“实践操作法”。

通过提出问题，引导学生思考和探究，通过实际操作，让学生掌握用尺规作角的方法。

六. 教学准备1.准备直尺、圆规等作图工具。

2.准备相关的教学PPT或黑板。

七. 教学过程1.导入（5分钟）通过提出问题：“我们如何用直尺和圆规作出一个特定的角呢？”引发学生的思考和兴趣。

2.呈现（10分钟）通过PPT或黑板，呈现尺规作角的原理和步骤。

讲解并演示如何用尺规作角。

3.操练（10分钟）学生分组进行实践操作，尝试用尺规作出不同的角。

教师巡回指导，解答学生的疑问。

4.巩固（5分钟）学生汇报自己的操作结果，分享制作过程中的经验和问题。

教师点评并解答学生的疑问。

5.拓展（5分钟）引导学生思考：除了用尺规作角，还有没有其他方法可以作出相同的角？让学生进行思考和讨论。

6.小结（5分钟）教师引导学生总结本节课所学的知识，巩固对尺规作角的理解和掌握。

7.家庭作业（5分钟）布置相关的家庭作业，让学生进一步巩固和运用所学知识。

8.板书（5分钟）教师进行板书设计，总结本节课的主要内容和知识点。

以上是整个教学过程的设计，每个环节的时间安排如上所示。