当前位置：文档之家 › 第五章 光的衍射

第五章 光的衍射

  • 格式：ppt
  • 大小：7.87 MB
  • 文档页数：130

下载文档原格式

  / 130

合集下载

高中物理选修3-4第五章3光的衍射与偏振及激光

高中物理选修3-4第五章3光的衍射与偏振及激光

学习探究区
一、光的衍射 二、光的偏振
一、光的衍射
返回
问题设计
唐代诗人王维的诗句“空山不见人，但闻人语响”描写了一种常
见的“闻其声而不见其人”的物理现象.这种现象是如何形成的
呢？为什么声波容易发生衍射现象而光波不容易发生衍射现象呢？
答案 诗句中描写的是声波的衍射现象.
声波的波长较大，与日常生活中的物体可以相比，很容易发生明
1234
3.(对光的偏振的理解)将两个偏振片紧靠在一起，放在一盏灯 的前面，眼睛通过偏振片看到的光很弱.如果将其中一个偏振 片旋转180°，在旋转过程中会观察到( ) A.灯光逐渐增强，然后逐渐减弱 B.灯光强度保持不变 C.灯光逐渐增强，没有减弱现象 D.灯光逐渐增强，再减弱，然后增强到最亮
1234
一、光的衍射
返回
(2)圆孔衍射图样的特点： ①单色光的圆孔衍射图样中央亮圆的亮度高，外面是明暗相间的 不 等距 (填“等距”或“不等距”)的圆环，越向外，亮环亮度越 低 . ②白光的圆孔衍射图样中央亮圆为白色 ，周围是 彩色 圆环. (3)泊松亮斑：障碍物的衍射现象 ①在单色光传播途中，放一个较小的圆形障碍物，会发现在阴影中 心有一个 亮斑 ，这就是著名的泊松亮斑. ②图样特点：中央是一个亮斑，圆板阴影的边缘模糊，阴影外边有
典例精析 二、对光的偏振的理解
返回
A.到达O处光的强度会明显减弱 B.到达O处光的强度不会明显减弱 C.将偏振片B转动一个角度，使得O处光强度最大，偏振片B转
过的角度等于α D.将偏振片A转动一个角度，使得O处光强度最大，偏振片A转
过的角度等于α
典例精析 二、对光的偏振的理解
返回
解析 因为未放糖溶液时，A、B的偏振方向一致，故A、B间不 放糖溶液时，自然光通过偏振片A后，变成偏振光，通过B后到 达O.当在A、B间放糖溶液时，由于溶液的旋光作用，使通过A的 偏振光振动方向转动了一定角度，不能再通过B，A对，B错. 但当B转过一个角度，恰好使偏振片方向与经过糖溶液后的偏振 光振动方向一致时，O处光强为最强，故B的旋转角度即为糖溶 液的旋光度.所以C对.同理D也对. 答案 ACD

5光的衍射

5光的衍射

E(P)
E(P)=0
5.3 菲涅耳衍射和夫琅和费衍射 5.3.1 两类衍射现象的特点
1.菲涅耳衍射
光源或接收屏或两者距衍射屏有限远,以致入射 波的波面曲率不可忽略时的衍射.
若在离Σ 很近的 K1 处观察透过的光,可以看作是圆孔 的投影,这时光的传播大致可以看作是直线传播.
M
K1
K2
K3
K4

几何投影区 菲涅耳衍射区 夫朗禾费 衍射区
(上式椭圆积分)
3.夫琅和费近似
继续展开
r z1
x x1 2 y y1 2
2z1
x1 x y1 y x 2 y 2 x12 y12 z1＋ ... z1 2z1 2z1
取前三项 近似条件为:
x1 x y1 y x 2 y 2 r z1＋ z1 2z1
在 K2、K3 及其前后的范围内的衍射现象称为菲涅耳 衍射,而在很远处(如 K4 面上)的衍射现象称为夫朗和费 衍射.
M K1 K2 K3 K4
几何投影区 菲涅耳衍射区 夫朗禾费 衍射区

近场、远场的划分是相对的,对一定波长的光来说, 衍射孔径愈大，相应的近场与远场的距离也愈远.
5.3.2 两类衍射的近似计算公式
单独使用
单独使用 E1(P)
E2(P)
由巴俾涅原理可得到如下两个结论： 1.若 E1(P) = 0,则 E2(P) = E(P) .即放臵一个屏时,相 应于光场为零的那些点,在换上它的互补屏时,光场 与没有屏时一样. 2.若 E(P) ＝0,则 E1(P) ＝－E2(P).即在 E(P) ＝0 的 那些点,E1(P) 和 E2(P) 的相位差为 ,而两者在P点 的光强度相等.

第五章光的衍射(2)

第五章光的衍射(2)

~ i 2δ ~ ~ ik ( r1 + 2Δ ) E3 (θ ) = a0e sin cα = A0e sin cα
~ ~ i ( N -1) E N ( ) A0 e sin c
P点合振动的复振幅：
~ E (θ )
N 1

~ imδ A0 e s in cα
m 0
多缝衍射光强公式：
其中： ~ —衍射屏处复振幅及其它常量。 a0
e
ikrm
—第m个缝到P点的位相延迟。
sin c —单缝衍射因子，单缝在P 点引起的振动。
有：
~ ~ ~ ikr1 E1 (θ ) = a0 e sin cα = A0 sin cα
~ iδ ~ ~ ik ( r1 +Δ ) E2 (θ ) = a0 e sin cα = A0 e sin cα
sin
对多缝干涉因子
(
sin N sin
)
2
sin 0 sin N 2 当 时 ( ) 0 sin sin N 0

m' N
( m' 1, 2 N 1)
有干涉极小值。 两主极大间有N-1个极小值 。
对多缝干涉因子
(
sin N sin
)
r
r-OB
x
a
sin （P） I 0 I （ i

a (sin i sin i ) ）
2

a (sin i sin i)
① sini - sini’ = 0 时, I（Pi’）有极大值 即i ’ =i 时， I（Pi’）=Imax (反射定律成立时) ② sini - sini’ ≠ 0， 即 i ’ ≠i 时 只要满足 a>>λ， I（Pi’）≈ 0

高中物理：光学-光的衍射

高中物理：光学-光的衍射

高中物理：光学-光的衍射光的衍射是光学中的经典知识点，其在多个领域都有着广泛的应用，例如显微镜、天文望远镜等。

本文将详细介绍光的衍射的基本概念、衍射定理、夫琅禾费衍射以及常见的实验方法。

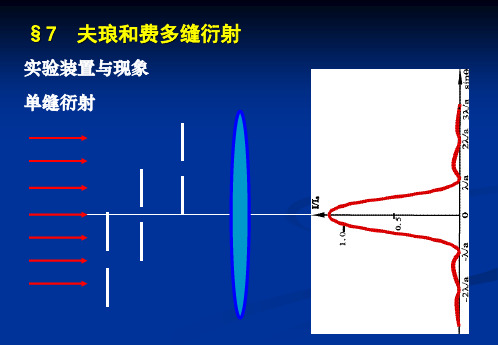
一、光的衍射的基本概念光的衍射是指光通过一个孔或者通过物体表面的缝隙后，光波会扩散成为一组新的光波，这种现象被称为光的衍射。

在光的衍射中，光波会形成一些明暗交替的区域，这些区域被称为衍射图样，其形状和孔或者缝隙的大小和形状有关。

二、衍射定理衍射定理是光学中最重要的定理之一，它是描述从一个孔或者一个光源丝的发射的光经过另一个孔或者缝隙后产生的光的波前的变化情况。

衍射定理可以用来计算衍射图案的形状，以及通过使用光的衍射图案来确定物体的大小和形状。

衍射定理的公式如下所示：sinθ = nλ/d其中，θ是衍射角，n是衍射序数，λ是光的波长，d是孔或者缝隙的宽度。

三、夫琅禾费衍射夫琅禾费衍射是一种典型的衍射现象，它是一种发生在单缝或双缝上的衍射现象。

夫琅禾费衍射的衍射图样是一组纵向的亮暗条纹。

夫琅禾费衍射的公式如下所示：dsinθ = nλ其中，d是缝隙的大小，θ是衍射角，n是衍射序数，λ是光的波长。

四、实验方法实验方法是研究光的衍射现象的重要手段。

常见的光的衍射实验方法包括单缝衍射实验、双缝干涉实验、格点衍射实验等。

（1）单缝衍射实验单缝衍射实验是研究光的衍射现象的最简单的实验方法之一，它可以通过一个狭窄的孔洞使光波扩散成为一个圆形的波前来观察光的衍射现象。

（2）双缝干涉实验双缝干涉实验是研究光的干涉现象的重要实验方法，它可以通过两个狭缝使光波扩散成为一组具有干涉现象的亮暗条纹。

（3）格点衍射实验格点衍射实验是一种研究光的衍射现象的实验方法，它可以通过一个光栅来使光波扩散成为一组具有规律的亮暗条纹。

五、练习题1. 一束波长为500nm的光穿过一个宽度为0.3mm的单缝后，经过距离1m的观察屏时，其衍射图样的第五个主极大的位置距离中心线的距离是多少？参考答案：0.30mm2. 光通过一组双缝（缝距为0.1mm，缝宽为0.05mm），在距离屏幕40cm处出现了一组亮暗条纹。

光的衍射ppt

光的衍射ppt

02
光的衍射理论
惠更斯-菲涅尔原理
波前相干叠加
惠更斯-菲涅尔原理是波动光学中的一个重要原理，它基于波前的相干叠加， 即波前的每一点都可以视为一个独立的子波源，这些子波源发出的子波在空 间某点处相互叠加，形成该点的总波幅。
波前干涉
当两个或多个波源的波前在空间某点相遇时，它们会相互叠加并产生干涉现 象。干涉现象表现为波前的加强或减弱，从而形成明暗相间的条纹。
衍射的分类
菲涅尔衍射
当光通过一个具有有限大小的孔或狭缝时，会发生菲涅尔衍射。菲涅尔衍射的明 暗条纹是交替出现的，且条纹间距与孔径大小有关。
夫琅禾费衍射
当光通过一个具有无限小的孔或狭缝时，会发生夫琅禾费衍射。夫琅禾费衍射的 明暗条纹是连续分布的，且条纹间距与波长和孔径大小有关。
影响衍射的因素
孔径大小
03
光的衍射实验
实验目的
探究光的波动性质
通过观察和实验，了解光的衍射现象和特点，验证光的波动性。
学习基本实验技能
通过实验操作，掌握基本的光学实验技能，如调节光学系统、观察和记录实验现象等。
了解现象背后的原理
探究光的衍射现象的原理，了解光的波动光学的基本理论。
实验原理01衍射现象 Nhomakorabea当光通过具有与波长相当的空间时，光会出现散射和传播方向的改变
光的衍射现象举例
阳光照射到树叶缝隙时，产生的衍射现象形成光斑。 在全息照相中，利用光的衍射现象可以记录并再现物体的三维图像。
光的衍射的物理意义
衍射现象是光的波 动性的表现之一。
光的衍射现象在光 学仪器、信息处理 和通信等领域有广 泛应用。
光的衍射现象说明 光具有波动性和粒 子性，是物理学中 基本概念之一。

大学物理光的衍射

大学物理光的衍射
XX,
汇报人：XX
01
02
03
04
05
06
光的衍射是指光在传播过程中遇到障碍物时，会绕过障碍物继续传播的现象。
光的衍射是光的波动性的表现，与光的干涉、反射等现象一起构成了光的传播规律。
光的衍射现象在光学、物理学、天文学等领域有着广泛的应用。 光的衍射现象的发现，为光的波动说提供了有力的证据，推动了光学的发展。
单缝衍射：光通过单缝时，形成明暗相间 的条纹
双缝干涉：光通过双缝时，形成明暗相间 的条纹
薄膜干涉：光通过薄膜时，形成彩色的条 纹
光栅衍射：光通过光栅时，形成彩色的条 纹
菲涅尔衍射：光通过菲涅尔透镜时，形成 彩色的条纹
光子衍射：光子通过狭缝时，形成明暗相 间的条纹
光的衍射：光在传 播过程中遇到障碍 物时，会发生衍射 现象
衍射图样：单缝衍 射图样是明暗相间 的条纹，条纹间距 与狭缝宽度有关
单缝衍射的条纹间距与狭缝 的宽度、光的波长和观察屏 的距离有关。
单缝衍射是光的衍射现象之 一，当光通过狭缝时，会在 其后形成明暗相间的条纹。
单缝衍射的条纹亮度与狭缝 的宽度和光的强度有关。
单缝衍射的条纹形状与狭缝 的形状有关，可以是直线、
光的波动性：光 波在传播过程中 具有周期性和振 幅变化的特点。
干涉现象：当两 束或多束相干光 波相遇时，它们 在空间某些区域 会相互加强或减 弱，形成明暗相 间的干涉条纹。
双缝干涉实验： 通过双缝干涉实 验可以观察到明 暗交替的干涉条 纹，证明了光波
的波动性。
干涉条件：只有 相干光波才能产 生干涉现象，而 相干光波需要满 足频率相同、振 动方向相同和相 位差恒定等条件。
曲线或折线等。
光学仪器制造：利用 单缝衍射现象制造各 种光学仪器，如望远 镜、显微镜等。

ch5 光的衍射

第五章 光的衍射5.10 用波长为632.8nm 的激光束测量单缝宽度，若测得中心附近两侧第五个极小间的距离为6.3cm ，缝与屏的距离为5cm ，试求缝宽？ 解：上述装置中激光束射到单缝上可视为平行光入射，在逢后5cm 接受，这是夫琅禾费衍射.(参考教材例题5.2)单逢夫琅禾费衍射，产生极小值的条件为sin 1,2n n n θλ==±±据题意：25 3.1510sin sin 5a λθθ-⨯=≈9425632.81055100.53.1510a m mm ---⨯⨯⨯∴=⨯=⨯5.11测得一细丝的夫琅禾费零级衍射斑的宽度为1cm ，已知入射光波波长为632.8nm ，透镜焦距为50cm ，求细丝的直径？ 解 ：由sin a θλ=得：0.5sin 0.0150θ≈= 632.863280632.80.01a nm m μ===5.12折射率分别为n 1和n 2、厚度为d 、表面平行的两块玻璃片彼此对接，覆盖一定宽度的狭缝，两片各盖住缝宽的一半，单色平行光垂直入射到狭缝上.在什么条件下夫琅禾费衍射图样的中心是暗的？ 解：衍射图样的中心是在衍射角0θ= 的方向缝的上、下部相对应点在P 点的光程差为：12(n n )d ∆=-当21)2m λ∆=+（时，衍射图样中心处为暗纹.若取0m =，则12()2n n d λ-=时，P 点处为暗纹.5.13一束直径为2mm 的氦氖激光（λ=632.8nm ）自地面射向月球.已知月球离地面的距离为3.76×105km.问在月球上得到的光斑有多大？不计大气的影响.若把这样的激光束扩大到直径为2m 和5m 后在发射，月球上的光斑有多大？ 解:激光束的发射角1031.221.226328100.386210Dmradλθθ--∆=⨯⨯∆==⨯光斑半径为：145.163R L Km θ=∆⨯=；则其直径为：2R 290.272k m φ==若D=2m ，则290.272m φ=；若D=5m ，则116m φ=. 可见衍射斑的大小与衍射孔径的大小成反比. 5.14一会聚透镜，直径为3cm ，焦距f 为20cm ，问：（1）为了满足瑞利判据，两个遥远的点状物体必须有多大的角距离？（设λ=550nm ）. （2）在透镜焦平面上两个衍射图样的中心相隔多远？解: (1)由瑞利判据，当两个点状物体的角距离等于零级衍射斑的角半径时，则可分辨，则有：50 1.222.2410rad Dλθθ-===⨯(2)两衍射斑中心距离（透镜焦平面上）252010 2.2410 4.47310L f m θμ--=⋅=⨯⨯⨯=5.18由紫光在（λ=400nm ），绿光（λ=500nm ）和红光（λ=750nm ），三种波长组成的平行光垂直入射到一个光栅上，光栅常数为0.005mm ，用'1f m =的透镜把光谱会聚于焦平面上，问：第二级红线、第三级绿线和第四级紫线之间的距离为多少？解：第二级红线衍射角的正弦：2322750sin 0.3510d λθ-⨯===⨯ 第三级绿线衍射角的正弦：3333500sin 0.3510d λθ-⨯===⨯ 第四级紫线衍射角的正弦:4344400sin 0.32510d λθ-⨯===⨯ 可见第二级红线与第三级绿线在屏上重合，且与第四级紫线的距离为42(sin sin )1(0.320.30)0.0220L f m mm θθ'≈-=⨯-==5.20用波长为0.5890µm 的单色光照射一光栅，已知该光栅的缝宽0.0010a mm =，不透明部分宽度0.0025b mm =，缝数NN=105条.试求： （1）中央峰的角宽度；（2）中央峰内干涉主极大的数目； （3）第一级谱线的半角宽度. 解：（1）由22aλθθ=∆=得：0.58902 1.1781rad θ=⨯= （2）中央峰内主极大数目为：3.5d a b m a a+=== 此时中央峰内有0级到±3级干涉主极大K 2317∴=⨯+=条（3）中央峰的角宽度为：cos nd λθθ∆=其中：cos θ==代入数据得：-61.710rad θ∆=⨯5.21一块平面透射光栅，在1mm 内有500条狭缝，现对钠光谱（0.5893m λμ=）进行观察，试求：（1）当光束垂直入射到光栅上时，最多能看到几级光谱？ （2）当光束以30°角入射时，情况如何？解 ：据题意有：当光垂直入射时31210500d mm -==⨯ maxsin 3.14d d m θλλ==≈当光束以30°角入射时：(sin30sin )o d m θλ+=max (sin 30sin 90)5o o d m λ+==（取整数）5.22一块透射光栅由2N+1条缝组成，除中央一条缝的宽度为2a 外，其他2N 条缝的缝宽均为a ，相邻各缝之间的间隔d=4a.试分析此光栅在焦平面上的光强分布与各缝均为a ，间隔为d=4a 的光栅的异同.（提示：将2N+1条缝分成两部分，考虑两部分之间的相干叠加.）解：将2N+1条缝分成两部分，上半部分N 条，下半部分N 条，两部分的光程差 对于0级：sin 0 0 I 4I θ=∆==上 对于1级： sin asin I 4I 44daλλλθθ====上对于2级：2sin asin I 022d a λλλθθδπ===== 对于3级：23333sin asin I 2I d 442a λλθθλδπ===== 对于4级：缺级4da = 对于5级： 55sin I 2I 2d λθδπ===上 对于6级：6sin 3 I 0d λθδπ=== 对于7级：77sin I 2I 2d λθδπ===上 比较：相同：极大位置相同，0级光强相同. 不同：奇数级次强度减半，偶数级次强度为0.5.30在菲涅耳圆孔衍射中，若以一枚硬币作为圆盘（01cm ρ=），令0R r =，取0.5m λμ=，若要求圆盘中心有足够的亮度（圆盘挡住的部分恰好为一个半波带），则光源与观察屏的距离应为多少？解：第一个半波带被档时，屏上光振动的合振幅A 为：111122o a aA a a a =-=-=- 其中a 0是光波自由传播时，即波面没有被遮蔽时的振幅，因为102a a ≈，所以屏上的光强为： 22104a I A I ===5.32单色平行光垂直照射到直径30d cm =的圆孔上，在离圆孔 3.6r km =处的平面上产生菲涅耳衍射图样.如果要在离孔4r cm =处的屏上观察到一个相似的衍射图样，圆孔的直径应改为多少？解：当圆孔所的波带数相同时，得到相似的衍射图样.平行光入射时，2n R r ρλ→∞=，据题意：2222121201020102r d d r r r ρρλλλλ==或 222120202211301014(310) 3.610r r d d d r r λλ-===⨯⨯⨯ 24222110 1101d m d m cm --=⨯=⨯=5.33一块很大的平行平面玻璃，在其中央镀一层圆形透明薄膜，膜后500d nm =，折射率1.5n =，直径1D mm =，当可见光垂直入射时，哪一个波长的光可以在哪一个点获得光强为不镀膜时九倍？（忽略玻璃板与薄膜的损耗）. 解：设不镀膜时P 0点光振动的合振幅为：102a a =镀膜后，要求合振幅03A a =，可以写为：11103322a aA a a =+== 可以设想：所镀膜厚产生π的相位差所镀膜区域大小对P 0点是一个半波带，即第一个半波带在P 点产生的振幅是a 1，相位与第二个半波带相同.从第二个半波带到∞个的合振幅为：26144223435()() 2222222a a a a a aa a a a a a a ∞∞-+-++=-+--+--++≈- 镀膜后：22103322a aA a a =--≈-=（1） 由于镀膜使相位改变π，即波长满足以下关系式：(1)2n d λ-=2(1)500n d nm λ=-=（2）镀膜部分为第一个半波带，即：201r ρλ= 2204(0.5)500510r mm ρλ-===⨯5.36半波带片第五环半径为1.5mm ，求波带片对于波长为0.5m μ的单色光的焦距'f 和第一环半径r ，若波带与屏幕之间充以折射率为n 的介质，将发生什么变化？解：由2f n ρλ=，45 1.5,510,5mm mm n ρλ-==⨯=得：241.5900 5105f mm -==⨯⨯又因为j ρ=41,900,510j f mm mm λ-===⨯得：0.67mm ρ==若充以介质后，光波波长将变小，其焦距将变长.。

_第五章 光衍射技术

L1 S L2 Pθ b θ P0
单缝夫琅和费衍射的实验装置
现代光学测试技术
单缝衍射
I • ②单缝夫琅和费衍射强度分布
• 用振幅矢量法或衍射积分法都可以得到缝宽为b的单缝夫 琅和费衍射光强分布表达式：
sin I I0
2
I0
1
• 其中
2 b

b
π b sin
现代光学测试技术
衍射计量不足之处
（1）绝对量程比较小，量程范围约0.01~1.5mm 超过此范围必须用比较测量法 （2）当ω小时，衍射条纹本身比较宽，不容易获得精确测量 （3）R大，装置外型尺寸不能紧凑。限制了衍射计量的应用范围
现代光学测试技术
§5-2 激光衍射计量技术
现代光学测试技术
主要内容
现代光学测试技术
图中曲线表示探测器置于A点或B点的 信号变化。当用一个探测器测量时，， 其位置应放在灵敏度和动态范围最好 的A点或B点进行。但在用一个探测器 的情况下，激光功率的不稳定性一级 被测物体有横向位移时，对测量结果 有很大影响。因此，可能认为放在A 和B点的两个探测器用差值信号可以 改善测量情况，但是从图5-6的曲线C 来看，灵敏度是有保证的，但仍然不 能消除这种基本方案的缺点-----激光 功率不稳定一级被测物在光束中位移 造成的测量误差。因为，衍射光强变 化时C的斜率变化。
设
w （缝宽），则衍射条纹的光强分别按式（5-6）为
w I I 0 sin c
2
对sinc函数，其定义是 sin c ( w ) 设
w
sin ( w )
w
，由式（5-8），则式（5-7）可写为
sin 2 I I0 2

光的衍射现象

S
观察比较方便，但定量计算却很复杂（需完成复杂 的Fresnel积分）。
2.Fraunhofer衍射（远场衍射）
光源和光屏到障碍物或孔隙的距离可以认为是无限远 的，即实际上使用的是平行光束。比Fresnel衍射更重 要。
L2
L1பைடு நூலகம்
S
o
Fraunhofer衍射可通过使用简单实用的方法——半波带 法得到重要而近似准确的结果。
a
a
2
U ( ) C eikr dx
a
2
C eikxsin dx
a
C
eikx sin
ik sin
x a
|2
x a 2
2
2
C
1
ika sin
ika sin
[e 2 e 2 ]
ik sin
C 1 2i sin( ka sin )
ik sin
2
2C
sin(
ka
sin
2
)
ac
sin
k sin
d
在光孔和接收范围满足傍轴条件情况下， 0 0，
r r0 （场点到光孔中心的距离）
U (P) i U 0(Q)eikrd
r0 (0 )
三、衍射现象的分类
分类的标准——按光源和考察点（光屏）到障 碍物距离的不同进行分类。
1 Fresnel衍射（近场衍射）
障碍物（孔隙）距光源和光屏的距离都是有限的，或 其中之一是有限的。
A
(b) n为偶数
半波带法中的振动矢量图
A(P0 )
1 2
[ A1
(1)n1
An
]
讨论：1）自由传播情形，整个波前裸露
f (n ) 0,从而An 0

光的衍射课件

光的衍射
一、光的衍射 1．衍射现象：光能够绕过障碍物而到达“阴影”区域的 现象． 2．产生明显衍射现象的条件：障碍物或孔的尺寸比光波 波长小或与光波波长差不多时．
二、几种不同的衍射现象 1．圆孔衍射 (1)现象 ①用点光源照射直径较大的圆孔时，在屏上会出现一个明 亮的圆形光斑，这是光直线传播的结果． ②用点光源照射直径足够小的圆孔时，在屏上会出现一些 明暗相间的圆环，这是光发生衍射的结果． (2)衍射图样的特点 明暗相间的环状条纹，中央为圆形亮斑．
(2)圆孔衍射图样
①中央是大且亮的圆形亮斑，周围分布着明暗相间的同心 圆环，且越靠外，圆形亮条纹的亮度越弱，宽度越小．如图所 示．
②只有圆孔足够小时，才能得到明显的衍射图样．在圆孔 由较大直径逐渐减小的过程中，光屏依次得到几种不同现象 ——圆形亮斑(光的直线传播)、光源的像(小孔成像)、明暗相 间的圆环(衍射图样)、完全黑暗．
【解析】 图①中出现明暗相间的条纹，是衍射现象，图 ②中出现圆形亮斑．只有障碍物或孔的尺寸比光波波长小或跟 波长相差不多时，才能发生明显的衍射现象．图①是光的衍射 图样，由于光波波长很短，约在10－7m数量级上，所以图①对 应的圆孔的孔径比图②所对应的圆孔的孔径小．图②的形成可 以用光的直线传播解释．
【解析】 光的干涉、衍射都是波叠加的结果，都能说明 光具有波动性，干涉条纹是等间距，而衍射条纹是不等间距 的，白光的干涉和衍射条纹都是彩色的，故D选项正确．
【)单缝衍射图样 ①缝变窄，通过的光变少，而光分布的范围更宽，所以亮 纹的亮度降低． ②中央亮条纹的宽度及条纹间距跟入射光的波长及单缝宽 度有关．入射光波长越长，单缝越窄，中央亮条纹的宽度及条 纹间距就越大．
③用白光做单缝衍射时，中央亮条纹是白色的，两边是彩 色条纹，中央亮条纹仍然最宽最亮.
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2 2
( p) 0光波通行无阻时自由光场E 0 =1 + 2
巴比涅原理中的一对互补屏
在衍射积分式中，积分区间(光孔)
( p)=E ( p)+E ( p) E 1 2
( p) ,则其互补屏之衍射场就容易地获 得， 意义:一旦求得E 1
( p)=E ( p)-E ( p) E 2 1
2
夫琅和费衍射实验装置
2
( x, y) 1 exp[ik ( z x y )] E ( x , y ) exp[ ik ( xx yy )]dx dy E 1 1 1 1 1 1 1 i z1 2 z1 z 1
2828
衍开孔平面上光的分 布均匀则透镜紧贴矩孔
11
5.1 光的衍射引言
1、光的衍射概论 光波在传播过程中遇到障碍物时，会偏离原来的传播方向
弯入障碍物的几何影区内，并在障碍物后的观察屏上呈现
光强的不均匀分布，这种现象称为光的衍射。 衍射使屏障以后的空间光强分布，既区别于几何光学给出 的光强分布，又区别于光波自由传播时的光强分布，衍射 光强有了一种重新分布！
6
2、基尔霍夫标量衍射理论
光是一种电磁波，光通过小孔的衍射问题可以作为
电磁场的边值问题来求解。这种方法的缺点是比较复杂。 实际所用的衍射理论都是一些近似的解法。本章主 要介绍的是基尔霍夫标量衍射理论（也是一种近似理论）。 可以解决多数的光学仪器中的衍射问题。 其适用条件是： 傍轴、自然光！ 这在实验上是不难被满足的。
exp(ikr ) E ( P) c k ( )E(Q) r d
14 14
菲涅尔假设
0, K ( ) 1 , K ( ) 0
2
且有
K ( )
惠更斯—菲涅耳原理的缺陷
（1）人为假设了k(θ),未给出k(θ)和c的具体形式;
（2）假设当 θ≥π/2时，k(θ)＝0。事实证明，该假设不正确;
这一近似称为夫琅和费近似，在此条件下看到的衍射现象称 为夫琅和费衍射，观察屏所处的区域称为夫琅和费衍射区
exp(ikz1 ) ik 2 ~ E ( x, y ) exp[ ( x y 2 )] iz1 2 z1


ik ~ E ( x1, y1 ) exp[ ( xx1 yy1 )]dx1dy1 z1
这一近似即为菲涅耳近似。观察屏位于这一近似区域内所 观察到的衍射现象即为菲涅耳衍射，此时观察屏所处的区 域为菲涅耳衍射区。近似后菲涅耳-基尔霍夫衍射公式为：
1 (Q) exp(ikr )d E ( x, y) E ( P) E i z1 2 2 ( x x ) ( y y ) 1 1 1 E ( x1 , y1 ) exp ik[ z1 ] dx1dy1 i z1 2 z1 2 z1
K 1 cos 1 2
即近似地把倾斜因子看作常量，不考虑它对衍射的影响
20
（2）同时取r≈z1，认为r变化对振幅影响可略，但r对相位的影响
不可略 。
1 (Q) exp(ikr )d E ( P ) E 取上面两个近似后有： i z1
强调:
(Q) ，将产生不同的衍 不同的光孔形状（Σ）、不同的瞳函数 E
2 2 2 k [( x x ) ( y y ) ] 1 1 中的第5项 3 8z1
由于菲涅尔衍射光斑只是略有扩大，取 ( x x1 )2 ( y y1 )2 2
4 3 3 z cm 16000cm 5 4 6 10
3 1
即 z1 25cm
(Q)=0 (1)、无穷远面 2：E (Q)=0 (2)、光屏面 ：E
1
(3)、光孔面 0 对场点有贡献。
1717
衍射积分公式简化为：
( P) A (Q) exp(ikr ) cos(n, r ) cos(n, l ) d E E i r 2
15 15
5.3 菲涅耳-基尔霍夫衍射公式
基尔霍夫指从亥姆霍兹方程方程出发，用格林公式，在k.r >> 1 近似下,给出了无源空间边值定解的积分表达式： 基尔霍夫的新贡献是：
( P) A E (Q) cos(n, r ) cos(n, l ) exp(ikr) d E i 2 r
A exp(ikr ) cos(n, r ) cos( n, l ) E ( P) E (Q) d i r 2
19
（一）傍轴近似（初步近似）
当孔径范围及观察范围远小于两 者之间距的情况 。 单色平面波垂直入射时： （1）cos(n,r)=cos（θ）≈1,因此倾斜因子
26
为满足夫琅禾费衍射的成立条件，要求
x12 y12 k 2 z1
即
z1 x12 y12
取 x1 y1 1cm
160m

菲涅尔衍射和夫琅禾费衍射的观察
27
5.4 矩孔和单缝的夫琅和费衍射
一、装置与实验现象 S：单色点光源 L1 、 L2：透镜 平行光入射，焦点怎么 偏离了P0点？
应用二项式展开 ，得 2 2 2 2 2 1 x x1 y y1 1 x x1 y y1 r z [1 ]
1
2
z12
8
z12

( x x1 ) 2 ( y y1 ) 2 [( x x1 ) 2 ( y y1 ) 2 ]2 =z1 1 2 4 2 z 8 z 1 1
ik exp(ikz1 ) 2 2 E ( x1 , y1 ) exp [( x x1 ) ( y y1 ) ] dx1dy1 i z1 2 z1
23
在孔径外的复振幅为0则上式可写为：
ik exp(ikz1 ) 2 2 E ( x, y) E ( x1 , y1 ) exp [( x x1 ) ( y y1 ) ] dx1dy1 i z1 2 z1
——菲涅耳衍射公式
2424
如进一步增大z1，将观察屏移到离衍射开孔更远的地方，菲涅尔 衍射公式中的第四项对位相的贡献远小于π时,忽略第四项，则 有
x 2 y 2 xx1 yy1 x 2 y 2 xx1 yy1 x12 y12 z1 r z1 2 z1 z1 2 z1 z1 2 z1
z1 f
2 x y x y E ( x, y) exp[ik ( f )] E ( x1 , y1 ) exp[ ik ( x1 y1 )]dx1dy1 i f 2f f f
1
2
x y 令l sin x , w sin y f f
P点的复振幅可写为
( P) ，而积分核 exp(ikr ) 射场 E
总是这个形式。
2121
（二）菲涅耳近似和夫琅和费近似 要对相位因子指数中的r进行积分是 比较困难，因此必须做更精确的近 似来进行简化
如右图在衍射开孔平面和观察屏平面建立坐标系，有：
r z12 ( x x1 ) 2 ( y y1 ) 2 z1[1 ( x x1 2 y y1 2 1 2 ) ( ) ] z1 z1
x2 y 2 xx1 yy1 x12 y12 [( x x1 )2 ( y y1 )2 ]2 z1 3 2 z1 z1 2 z1 8z1
2222
当z1大到使第四项以后各项对位相 k· r 的作用远小于π时， 忽略第四项以后的高次项：
( x x1 )2 ( y y1 )2 x 2 y 2 xx1 yy1 x12 y12 r z1 z1 2 z1 z1 2 z1 2 z1 2 z1
菲涅耳原理的实质：无源空间边值定解，即波前决定一切，决 定观测结果;
其推论：当再现或重构相同的波前，必将再现相同的观测结果，
即使原物不复存在。------ 全息术的思想基础
1818
5.3．菲涅耳衍射和夫琅禾费衍射
衍射积分公式计算比较复杂，为了能够详细讨论衍射现象，
在计算的过程做一些近似以便简化计算。
——夫琅和费衍射公式 夫琅和费衍射公式要比菲涅耳衍射公式简单。 实际应用中，对夫琅和费衍射可直接由以上公式进行计算
2525
例：不透明屏上圆孔的直径为2cm，受波长为600nm的平行光照射， 试估算菲涅尔衍射区和夫琅禾费衍射区起点到圆孔的距离。
解：为满足菲涅尔近似的成立条件，要求
x2 y 2 xx1 yy1 x12 y12 [( x x1 )2 ( y y1 )2 ]2 kr k ( z1 ) 3 2 z1 z1 2 z1 8z1
7
3、衍射系统及其分类
前场 照明空间,照明波一般较简单， 后场 衍射空间,衍射波一般较复杂。 理论目标是
(x , y ) E ( x, y) E 0 0
8
衍射的分类
99
4、衍射巴比涅原理 反映互补屏的两个衍射场之关系
( p) 1屏造成的衍射场E 1 ( p) 屏造成的衍射场E
d 波前上作为次波源的微分面源； (Q) 次波源自身的复振幅； E exp(ikr ) 次波源发射球面波到达场点 r K ( ) 倾斜因子用以表明次波源的发射并非各向同性
引入常数c,
exp(ikr ) dE ( P) cK ( ) E (Q) d r
具有实际意义与理论意义。
衍射现象显著，出现衍射花样。
衍射现象过于明显向散射过渡。
5
衍射是一切波动均具有的传播行为。与声波衍射、水波衍射相 比，光波衍射不易观察到。 原因两点： 一 是可见光的波长极短， 二 是普通光源是非相干的面光源。 既要求光源是足够小的“点”，又要求在远处有足够的光强，