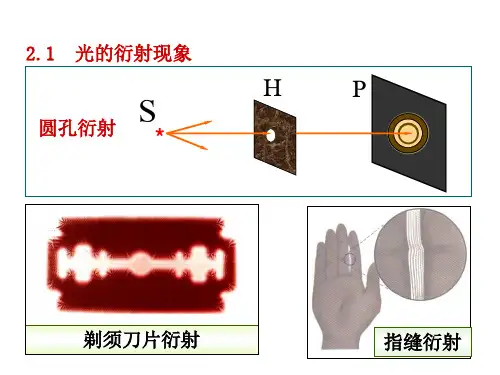
第2章 光的衍射
- 格式:ppt
- 大小:2.54 MB
- 文档页数:71






第二章光的衍射§1 惠更斯——菲涅耳原理一、衍射现象即不沿直线传播而向各方向绕射的现象。
定义:光绕过障碍物偏离直线传播而进入几何阴影,并在屏上出现光强不均匀的分布现象——光的衍射。
当障碍物或孔隙的线度比波大很多,通常都显示光的直线传播现象。
声波和水波的衍射可常见。
例:人在房间说话,另一房间的人能听见。
又,把杨氏装置中的两孔之一遮蔽,使光束通过单孔照射,仔细观察,屏上明亮区比直线传播所估计的要大且出现明暗不均匀的现象。
二、惠更斯——菲涅耳原理惠更斯:任何时刻波面上的每一点都可作为次波的波源,各自发出球面次波,在以后时刻,所有这些次波波面的包络面形成整个波在该时刻的新波面。
原理较粗糙,不能解释干涉、衍射甚至还有倒退波的存在。
它不涉及波的时空周期特性——位相、波长、振幅,而衍射现象有明暗相间的条纹出现。
波动有两个基本性质:(1)振动在空间的传播;(2)具有时空周期性,能够相干迭加。
“次波”概念反映前一基本性质,也是成功之处。
但当时对波动性认识肤浅,惠更斯并不知光速有多大,只把光看成空气中的声波(纵波),其“振动”也是非周期性的无规则脉冲,因而原理中并没反映出波的时空周期性.菲涅耳的改进因牛顿威望极高,微粒说影响极大,光的波动理论停滞不前,几乎过了一百年,到了十九世纪,杨反用波的迭加原理解释了薄膜的颜色,首先提出“干涉"一词概括波与波的相互作用,为了验证自己的理论,做了一个双缝干涉,即杨氏干涉实验,他并对出现于阴影边缘附近的衍射条纹给出了正确解释,但这些富有价值的光学研究并没被重视,直到1818年,在巴黎科学院举行的以解释衍射现象为内容的有奖竞赛会上,年青的菲涅耳出人意料地获胜,才开始了光的波动说的兴旺时期,那次竞赛会上,评委中有许多著名的学者,如毕奥、拉普拉斯、泊松,他们都是微粒说的拥护者,竞赛题目的具体表达式带有明显的有利于微粒说的倾向性.然而,菲涅耳吸收了惠更斯的次波概念,阐述的次波相干迭加的新观点具有极大说服力,使反对派马上接受了,会后泊松又仔细审核菲涅理论,并用圆盘衍射,屋圆盘中心轴线上应有亮斑,看来似乎不可思议离奇的结论,不久,在实际中阿喇果果真发现了这一惊人的理论,这一发现对惠——菲原理是十分有力的支持. 惠-—菲原理:波面上每个面元ds 都可看成是新的振动中心,它们又发出次波,在空间某一点p 的振动是所有这些次波在该点的相干迭加。

第二章 光的衍射1. 单色平面光照射到一小圆孔上,将其波面分成半波带。
求第к个带的半径。
若极点到观察点的距离r 0为1m ,单色光波长为450nm ,求此时第一半波带的半径。
解:2022r r k k +=ρ 而20λk r r k +=20λk r r k =- 20202λρk r r k =-+将上式两边平方,得 422020202λλρk kr r rk++=+略去22λk 项,则 λρ0kr k =将 cm 104500cm,100,1-80⨯===λr k 带入上式,得cm 067.0=ρ2. 平行单色光从左向右垂直射到一个有圆形小孔的屏上,设此孔可以像照相机光圈那样改变大小。
问:(1)小孔半径满足什么条件时,才能使得此小孔右侧轴线上距小空孔中心4m 的P 点的光强分别得到极大值和极小值;(2)P 点最亮时,小孔直径应为多大?设此时的波长为500nm 。
解:(1)根据上题结论 ρρ0kr k =将cm 105cm,400-50⨯==λr 代入,得cm 1414.01054005k k k =⨯⨯=-ρ当k 为奇数时,P 点为极大值; k 为偶数时,P 点为极小值。
(2)P 点最亮时,小孔的直径为 cm 2828.02201==λρr3.波长为500nm 的单色点光源离光阑1m ,光阑上有一个内外半径分别为0.5mm 和1mm 的透光圆环,接收点P 离光阑1m ,求P 点的光强I 与没有光阑时的光强度I 0之比。
解:根据题意 m 1=R 500nm mm 1R mm 5.0R m 121hk hk 0====λr有光阑时,由公式 ⎪⎪⎭⎫⎝⎛+=+=R r R Rr r R R k h h 11)(02002λλ 得 11000110001105005.011620211=⎪⎭⎫ ⎝⎛+⨯=⎪⎪⎭⎫ ⎝⎛+=-R r R k hk λ4100011000110500111620222=⎪⎭⎫ ⎝⎛+⨯=⎪⎪⎭⎫ ⎝⎛+=-R r R k hk λ 按圆孔里面套一个小圆屏幕()13221312121212121a a a a a a a a p =+=⎥⎦⎤⎢⎣⎡+-+=没有光阑时 210a a =所以42/211200=⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=a a a a I I p4.波长为632.8nm 的平行光射向直径为2.76mm 的圆孔,与孔相距1m 处放一屏。