当前位置：文档之家 › 强度理论例题ppt课件

强度理论例题ppt课件

  • 格式：ppt
  • 大小：767.00 KB
  • 文档页数：10

下载文档原格式

  / 10

合集下载

14-强度理论-45页PPT资料

14-强度理论-45页PPT资料

1 2222422
2 2 2 2
2 32
对于塑性材料采用第三或者第四强度理论。
第三强度理论：

r3242

第四强度理论：
r4232
s
n
对于脆性材料采用第一强度理论。
一、最大切应力理论（第三强度理论）
材料的破坏取决于最大切应力，无论材料处于何种
应力状态,只要最大切应力 max达到材料单向拉伸
屈服时的 s 时，就发生屈服破坏。
破坏条件: max s
1 2131 2s0
13 s
强度条件:
1
3
s
n
n
安全系数
第三强度理论 （最大切应力 理论）
第四强度理论 （畸变能密度 理论）
屈服 屈服
r3
13
s
n
r4
1 2
122
2
32
3
12
s
n
1、塑性材料,除三向 拉伸以外。 2、脆性材料， 三向压缩。
同第三强度理论
四、单向与纯剪切组合应力状态的强度条件
适用范围:
塑性材料,除三向拉伸以外。 脆性材料，三向压缩。
二、畸变能理论（第四强度理论）
材料的破坏取决于畸变能密度，无论材料处于何种应
力状态,只要畸变能密度 v d 达到材料单向拉伸屈服时
的
v
0 d
时，就发生屈服破坏。
破坏条件: vd vd0
1 6 E 1 2 2 2 3 2 3 1 2 1 6 E s 2 0 s 2
单向拉伸的强度条件为： max 复杂应力状态的强度条件为： r
三、相当应力 r 的概念

第九章强度理论5

第九章强度理论5
第九章 复杂应力状态强度问题
本章主要研究： 关于材料静荷破坏（失效）的理论 弯扭与弯拉(压)扭组合强度计算 承压薄壁圆筒强度计算
2019/12/2
武汉体育学院体育工程与信息技术系
1
第九章 复杂应力状态强度问题
§1 引言 §2 关于断裂的强度理论 §3 关于屈服的强度理论 §4 强度理论的应用 §5 承压薄壁圆筒强度计算
4
畸变能理论-第四强度理论
理论要点
引起材料屈服的主要因素－畸变能, 其密度为 vd 不论材料处于何种应力状态，当
时, 材料屈服 vd vds,单拉
[ss ss ss] v d 1 6 E 1 2 2 2 3 2 3 1 2 vds单 , 拉 13Ess2
低碳钢,三向等拉，m a (s1 x s ,断3 )/裂2 0
低碳钢，低温断裂
2019/12/2
武汉体育学院体育工程与信息技术系
8
一种常见应力状态的强度条件
单向、纯剪切联合作用
s sm ma i nxsx 2sysx 2sy2x 2
s sm ma i nx s2 0s2 022 1 2ss242
ss1312s s242
塑性材料：
s2 0
sr3 s242[s]
sr4 s232[s]
2019/12/2
武汉体育学院体育工程与信息技术系
9
纯剪切许用应力
sr3 s242[s]
sr4 s232[s]
纯剪切情况下（s= 0）
塑性材料:
sr32[s]
19
பைடு நூலகம்
例题
2. 强度分析
ss133817
pD
d

第九章强度理论5-PPT精品文档

第九章强度理论5-PPT精品文档

2 s s max 1 0 s 0 2 2 2 s s 4 2 2 2 s min
s 1 1 2 2 s s 4 2 s 3
塑性材料：
2 2 s s 4 [ s ] r3
s2 0
( s s ) / 2 0 低碳钢,三向等拉， ,断裂 m ax 1 3
低碳钢，低温断裂
2019/3/19 武汉体育学院体育工程与信息技术系 8
一种常见应力状态的强度条件
单向、纯剪切联合作用
2 s s s s s max x y x y 2 2 x 2 s min
[
]
如采用第三强度理论
2 2 [s ] s s 4 151 . 3 MPa r3 a a
4. 讨论
对短而高薄壁截面梁, 除应校核smax作用处的强度 外,还应校核max作用处, 及腹板翼缘交界处的强度
2019/3/19
武汉体育学院体育工程与信息技术系
第九章 复杂应力状态强度问题
本章主要研究： 关于材料静荷破坏（失效）的理论 弯扭与弯拉(压)扭组合强度计算 承压薄壁圆筒强度计算
2019/3/19
武汉体育学院体育工程与信息技术系
1
第九章 复杂应力状态强度问题
§1 引言 §2 关于断裂的强度理论 §3 关于屈服的强度理论 §4 强度理论的应用
畸变能理论-第四强度理论
理论要点 引起材料屈服的主要因素－畸变能, 其密度为 vd 不论材料处于何种应力状态，当 时, 材料屈服
v d v ds ,单 拉
1 2 1 2 2 2 v s s ds, v 单拉 d 1 2 2 3 3 1 3 E 6 E

《强度理论教学》课件

《强度理论教学》课件
这些理论各有其适用范围和局限性，应根据具体问题和材料的特性选择合适的强 度理论进行计算和分析。
02
最大拉应力理论
理论概述
最大拉应力理论，也称为第一 强度理论，认为材料在最大拉 应力作用下发生断裂破坏。
该理论忽略了其他应力分量对 材料强度的影响，只考虑了最 大拉应力。
该理论适用于脆性材料，如玻 璃、陶瓷等，这些材料的断裂 主要是由于拉应力引起的。
04
能量守恒理论
理论概述
能量守恒理论是物理学中的基本原理之 一，它指出在一个封闭系统中，能量不 能被创造或消灭，只能从一种形式转化
为另一种形式。
这一理论在许多领域都有广泛的应用， 如热力学、电磁学、光学和力学等。
能量守恒理论是自然科学和工程学科的 重要基础，为人类认识自然界和解决实
际问题提供了有力支持。
04
流动法则描述了材料在受力过 程中应变的发展规律。
流动法则是基于实验观察和理 论分析得到的，描述了材料在 受力过程中应变的分布和演化
。
流动法则对于预测材料的变形 行为和稳定性具有重要的意义
。
流动法则可以通过实验和数值 模拟进行验证和应用。
屈服准则与流动法则的关系
屈服准则和流动法则是描述材料力学 行为的两个重要方面，它们之间存在 密切的联系。
为的强度准则。
该理论认为，当材料所受剪应力 达到某一极限值时，材料发生屈
服或断裂。
该极限值即为材料的剪切强度极 限。
应用场景
最大剪应力理论主要应用于分析材料在复杂应力状态下的强 度和稳定性问题，如机械零件的强度分析、结构的稳定性分 析等。
在工程实践中，该理论常用于设计、优化和校核各种机械零 件和结构的承载能力。
源技术等方面。

强度理论分析

强度理论分析
解：
y
y 2 x x 1 x ( x y ) 15 10 4 . E x 60MPa, y 120MPa 由上两式可求得:
故,
1 120MPa, 2 60MPa, 3 0 r3 1 3 120MPa < [ ]
用强度理论建立复杂应力状态下的强度条件的 方法可用示意图表示。
选用相应的
强度理论计算
ri
相当应力

材料破坏的两种形式——相应存在两类强度理论：
最大拉应力理论和最大拉应变理论：以断裂为破坏形式。 最大剪应力理论和形状改变比能理论：以屈服或显著塑性 变形为破坏形式。
二.强度理论
（一）最大拉应力理论
例题3:试用第三强度理论分析图示三种应 力状态中哪种最危险？ 90
30
90
10
90
90
10
r 3 80MPa r 3 100MPa r 3 90MPa

最危险
例题4 已知： 和 试写出第三和第四强度理论的表达式。 解：首先确定主应力
1 2 2 1 4 2 2 1 2 2 3 4 2 2
2

代入得：
1 1 2 2 2 3 2 3 1 2 s 2


令：
s n
得：强度条件为：
1 2 2 2 1 2 2 3 3 1 2 4．适用范围： 塑性材料。
1．理论认为：决定材料产生断裂破坏的主要因素是单元体的 最大拉应力 1，即无论材料处于复杂应力状 态或是简单应力状态，只要单元体中的最大拉 应力 1达到材料在轴向拉伸下发生断裂破坏时 的极限值 jx ，就将发生断裂破坏。 即 ：发生断裂破坏的条件为：

材料力学第9章强度理论幻灯片PPT

材料力学第9章强度理论幻灯片PPT

页 退出
材料力学
出版社 理工分社
9．3．2形状改变能密度理论〔第四强度理论〕 弹性体在外力作用下发生弹性变形，载荷在相应位移上可做功。如果所加外 力是静载荷，那么外力所作的功全部转化为弹性体的变形能。处在外力作用 下的微小体，其形状和体积都会发生改变，故变形能又可分为形状改变能和 体积改变能〔畸变能〕。单位体积内的形状改变能称为形状改变能密度〔畸 变能密度〕。在复杂应力状态下，形状改变能密度的一般表达式为
页 退出
材料力学
出版社 理工分社
法国科学家马里奥(E.Mariotte)在1682年提出最大线应变理论，后经修正为 最大伸长线应变理论，也称为第二强度理论。这一理论考虑了3个主应力对 脆性断裂的影响，能较好地解释石料或混凝土等脆性材料受轴向压应力而沿 纵向截面开裂的现象。铸铁受拉—压二向应力且压应力较大时，试验结果也 与这一理论接近。但是，按照这一理论，脆性材料在二向和三向受拉时比单 向拉伸承载能力会更高，而试验结果并不能证实这一点。 最大拉应力强度理论和最大伸长线应变理论均是针对脆性断裂的强度理论。 一般认为，前者适用于脆性材料以拉应力为主的工况，而后者适用于脆性材 料以压应力为主的工况。在工程实际应用中，以上两种强度理论均有应用。
页 退出
材料力学
出版社 理工分社
解〔1〕螺旋桨轴外外表A点的应力状态 如图9.1〔b〕所示，该点处于平面应力状态。根据公式〔8.5〕可得
那么3个主应力为
根据公式〔9.16〕得轴外外表A点的第三和第四强度理论的强度条件分别为
页 退出
材料力学
出版社 理工分社
〔2〕分析螺旋桨轴的内力 易得各横截面上的轴力及扭矩均一样。由根本变形的知识，在图示外载荷作 用下，横截面各点正应力相等，轴外外表各点的切应力到达最大值。由此可 知，轴外外表上的点即为危险点，且应力值分别为

【材料课件】第十章-强度理论

【材料课件】第十章-强度理论

《推导》
• 失效方程（或极限条件）
1
b
E
即 1(23)b
E
E
或 1(23)b
•强度条件
e q 1 (2 3 )b /n []
注意：
1. eq 为相当应力 equivalent stress
2. 适用条件：直至断裂，一直服从虎克定律
《评价》
主应力有压应力时，当 3 1 ，理论接近实验
但不完全符合 其他情况下，不如第一强度理论
• 平面应力状态，把最大拉应力理论与莫尔理论
的失效方程画在 1 3 坐标系中
• 只要主应力 1, 3 点落在区域内就是安全的
• 最大拉应 力理论
bc
• 莫尔理论
3 b
b
1
bc
§10.2 适用于塑性屈服的强度理论 一、最大剪应力（第三强度）理论（Tresca准则）
1773年，Coulomb提出假设
的线性组合是脆性破坏的原因
具体说：平面应力状态只要构件内有一点处 1 与 3
的线性组合, 满足简单拉伸失效与简单压缩两个边界条件 的失效方程，就发生断裂破坏
《推导》
1 3
3 0 时 1 b 抗拉强度极限 1 0 时3 bc抗压强度极限
由两个边界条件 b b/bc
于是
1
b bc
3
b
即 1bbc//nn3b/n或 1 [[ct]]3 [t]
《失效准则》
最大拉应力 1 是引起材料断裂的原因
具体说：无论材料处于什么应力状态，
只要微元内的最大拉应力 1 达到了单向拉伸
的强度极限 b ，就发生断裂破坏
《推导》
•失效方程（或极限条件）1 b 此时断裂
•强度条件

《强度理论 》课件

《强度理论 》课件
《强度理论》PPT课件
CATALOGUE
目录
强度理论概述强度理论的类型强度理论的计算方法强度理论的应用实例强度理论的未来发展
01
强度理论概述
机械工程
用于飞机、火箭等复杂结构的强度分析。
航空航天
土木工程
材料科学
01
02
04
03
用于研究材料的力学性能和失效机制。
用于设计和分析机械零件、结构件等。
总结词
03
强度理论的计算方法
静力计算方法是强度理论中常用的一种方法，主要用于分析结构在静力载荷作用下的响应。
静力计算方法概述
基于牛顿第二定律和弹性力学的基本原理，通过建立平衡方程和应力应变关系来求解结构的内力和位移。
基本原理
适用于分析结构在静力载荷作用建筑结构的强度分析是确保建筑物安全的重要环节，通过强度理论的运用，对建筑物的各个组成部分进行受力分析、稳定性评估和抗震性能研究。
总结词
在建筑结构的强度分析中，强度理论同样发挥了重要作用。通过对建筑物的梁、柱、板等各个组成部分进行受力分析，了解其在各种工况下的应力分布和承载能力。同时，结合建筑物的功能需求和地理环境，对建筑物的稳定性、抗震性能等进行评估。通过合理的强度分析，可以有效地避免建筑物在自然灾害或意外事故中发生倒塌或损坏，保障人们的生命财产安全。
详细描述
第二强度理论认为，材料在受到外力作用时，其破坏是由于最大剪应力达到材料屈服极限所引起的。当最大剪应力达到材料的屈服极限时，材料发生屈服破坏，即丧失了承载能力。
VS
形状改变比能达到材料屈服极限时发生屈服破坏。
详细描述
第三强度理论认为，材料在受到外力作用时，其破坏是由于形状改变比能达到材料屈服极限所引起的。当形状改变比能达到材料的屈服极限时，材料发生屈服破坏，即丧失了承载能力。

第四强度理论。

第四强度理论。
选用 28a 钢能满足剪应力的强度要求。
腹板与翼缘交界处的的强度校核 取 a 点分析

a
y M
max
a
I
84 ቤተ መጻሕፍቲ ባይዱ106 126.3 149.1MPa 4 7114 10
13.7 6 3 S a 122 13.7 (126.3 2 ) 22310 m *
*

a
Q S
对于 28a 工字钢的截面，查表得
I 7114108 m4
d 0.8510 2 m
I 24.6210 2 m S
最大剪应力为:
Qmax max I d S 200 103 24.62 10 2 0.85 10 2
95.5MPa
t=10mm，D=1000mm，[]=160MPa。
图（a）为汽包的剖面图。内壁受压强 p 的作用 。
图（b）给出尺寸。
y z (a) (b)
D
t
解：包围内壁任一点，沿直径方向取一单元体，单元体的 侧面为横截面，上，下面为含直径的纵向截面，前面为内 表面。
y
z
包含直径的纵切面 内表面 z 横切面
σ a =149.1MPa
由于材料是Q235钢，所以在平面应力状态下，应按第四强度理论 来进行强度校核。


r4

2
2 2 2 1 [( 1 2) ( 2 3) ( 3 1) 2

3
2
149.12 3 73.82 197 MPa
σ r 4 σ 100% 15.9% σ
应另选较大的工字钢。
若选用28b号工字钢，算得 r4 = 173.2MPa , 比 大

第六章强度理论 PPT

第六章强度理论 PPT
第六章强度理论
§6-1 强度理论得概念
σmax ≤ [σ ]
单向应力状态
τmax≤ [τ ]
纯切应力状态
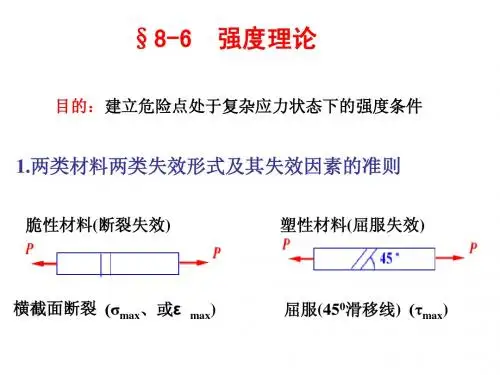
破坏形式(常温常压下) 脆性断裂破坏 塑性屈服破坏
为了解决复杂应力状态下得强度计算问题,不再采用直接通 过复杂应力状态得破坏实验建立强度条件得方法。
而就是致力于
观察与分析材料破坏得规律, 找出材料破坏得共同原因,
当危险点处于单向应力状态时: σmax = [σ]
当危险点处于纯切应力状态时: τmax = [τ]
例 已知铸铁构件上危险点得应
力状态。铸铁拉伸许用应力[t]
=30MPa。试校核:该点得强度。
[t] =30MPa
1＝29、28MPa, 2＝3、72MPa, 3＝0
解:1、首先根据材料与应力状态确 定失效形式,选择强度理论。
对于梁,除了需要作正应力与切应力强度计算外,当: 1) 某一截面上得剪力、弯矩同时达到或接近最大值时; 2) 梁得横截面宽度有突变得点处, 还需作主应力强度校核。
例 对某种岩石试样进行了一组三向受压破坏试验,结果如表 所示。
某工程得岩基中,两个危险点得应力情况已知。
A点1 210MPa, 3140MPa; B点 1 2120MPa, 3200MPa。
84 103 14.5102 11075.5 108
110.0MPa
200 103 267.4 106 11075.5108 0.9510
2
56.5MPa
r3 157.7MPa [ ] r4 147.2MPa [ ]
32a号工字钢既满足主应力强度要求,也满足最大正应 力与最大切应力强度条件。
解:1°作梁得FQ图与 M图。
2°正应力强度计算
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

126
15
9
300
z
a
y
对于翼缘和腹板交界处的a点:
5
（4）对C截面强度校核
126
Fsc左 75KN, Mc Mmax 75KN m;
最大正应力在b点:
15
9
300
z
max
但
Mc WZ
75103 0.611103
123MPa [ ]
max [ ] 5% [ ]
a by
所以仍在工程容许范围内,故认为是安全的.
65
M图（kN m） 20
作剪力图、弯矩图。
（2）确定危险截面 Fs,max 85KN, M max 75KN
危险截面可能是C左截面或D右：
C左 :
Fsc左 75KN, Mc Mmax 75KN m;
D右 :
FsD右 Fs,max 85KN, M D 654KN m;
（3）确定几何性质
最大正应力在b点:
max
MD WZ
65103 0.611103
106MPa [ ]
对于a 点:
126
15
9
300
z
a
by
M D ya
IZ
65103 135103 91.6 106
95.8MPa
FsD
S
* z
IZb
85103 2.69104 91.6106 9103
27.7MPa
8
按第三和第四强度理论校核:
r4
对于c 点:
126
15
9
300
c
z
a
by
9
FsD (Sz* )max IZb
85103 3.51104 91.6106 9103
36.2MPa
1 , 2 0,3
按第三和第四强度理论校核:
所以D截面强度足够。
10
一工字形截面梁受力如图所示，已知F=80KN,q=10KN/m,
许用应力 [ ] 120M。P试a 对梁的强度作全面校核。
126
F
F
q
15
A C
1m 2m
D
B
1m
2m
300
E
9
cz a

b
1
分析：
1、可能的危险点：
Mmax 作用面上 max作用点－距中性轴最远处；
FQmax 作用面上 max 作用点－中性轴上各点；
a
对于a 点:
Mc ya IZ
75103 135103 91.6 106
111MPa
6
Fsc Sz* IZb
75103 2.69104 91.6106 9103
24.5MPa
按第三和第四强度理论校核:
r3 [ ] 5% [ ]
r4
所以C截面强度足够。
a
7
（5）对D截面强度校核
FsD右 Fs,max 85KN, M D 65KN m;
M、FQ 都较大的作用面上、 都比较大 的点。
2
2、危险点的应力状态：
126
15
9
300
c
z
a
by
全面校核
b
a
c
（单向应力状态） （平面应力状态） （纯剪应力状态）
3
F
A C
1m 2m
F
q
DB
E
1m 2m
解： （1）求支座反 力并作内力图
75
(+)
20
(+)
(-)
5
Fs图（kN） (-) 75
85