第7章弯曲应力引言前一章讨论了梁在弯曲时的内力——剪力和弯矩。
但是，要解决梁的弯曲强度问题，只了解梁的内力是不够的，还必须研究梁的弯曲应力，应该知道梁在弯曲时，横截面上有什么应力，如何计算各点的应力。
在一般情况下，横截面上有两种内力——剪力和弯矩。
由于剪力是横截面上切向内力系的合力，所以它必然与切应力有关；而弯矩是横截面上法向内力系的合力偶矩，F时，就必然有切应力τ；所以它必然与正应力有关。
由此可见，梁横截面上有剪力Q有弯矩M时，就必然有正应力 。
为了解决梁的强度问题，本章将分别研究正应力与切应力的计算。
弯曲正应力纯弯曲梁的正应力由前节知道，正应力只与横截面上的弯矩有关，而与剪力无关。
因此，以横截面上只有弯矩，而无剪力作用的弯曲情况来讨论弯曲正应力问题。
在梁的各横截面上只有弯矩，而剪力为零的弯曲，称为纯弯曲。
如果在梁的各横截面上，同时存在着剪力和弯矩两种内力，这种弯曲称为横力弯曲或剪切弯曲。
例如在图7-1所示的简支梁中，BC段为纯弯曲，AB段和CD段为横力弯曲。
分析纯弯曲梁横截面上正应力的方法、步骤与分析圆轴扭转时横截面上切应力一样，需要综合考虑问题的变形方面、物理方面和静力学方面。
图7-1变形方面为了研究与横截面上正应力相应的纵向线应变，首先观察梁在纯弯曲时的变形现象。
为此，取一根具有纵向对称面的等直梁，例如图7-2(a)所示的矩形截面梁，并在梁的侧面上画出垂直于轴线的横向线m-m、n-n和平行于轴线的纵向线d-d、b -b 。
然后在梁的两端加一对大小相等、方向相反的力偶e M ，使梁产生纯弯曲。
此时可以观察到如下的变形现象。
纵向线弯曲后变成了弧线''a a 、''b b , 靠顶面的aa 线缩短了，靠底面的bb 线伸长了。
横向线m -m 、n -n 在梁变形后仍为直线，但相对转过了一定的角度，且仍与弯曲了的纵向线保持正交，如图7-2(b)所示。
梁内部的变形情况无法直接观察，但根据梁表面的变形现象对梁内部的变形进行如下假设：(1) 平面假设 梁所有的横截面变形后仍为平面．且仍垂直于变形后的梁的轴线。
(2) 单向受力假设 认为梁由许许多多根纵向纤维组成，各纤维之间没有相互挤压，每根纤维均处于拉伸或压缩的单向受力状态。
根据平面假设，前面由实验观察到的变形现象已经可以推广到梁的内部。
即梁在纯弯曲变形时，横截面保持平面并作相对转动，靠近上面部分的纵向纤维缩短，靠近下面部分的纵向纤维伸长。
由于变形的连续性，中间必有一层纵向纤维既不伸长也不缩短，这层纤维称为中性层(图7-3)。
中性层与横截面的交线称为中性轴。
由于外力偶作用在梁的纵向对称面内因此梁的变形也应该对称于此平面，在横截面上就是对称于对称轴。
所以中性轴必然垂直于对称轴，但具体在哪个位置上，目前还不能确定。
考察纯弯曲梁某一微段dx 的变形(图7-4)。
设弯曲变形以后，微段左右两横截面的相对转角为d ?，则距中性层为y 处的任一层纵向纤维bb 变形后的弧长为式中，ρ为中性层的曲率半径。
该层纤维变形前的长度与中性层处纵向纤维OO 长度相等，又因为变形前、后中性层内纤维OO 的长度不变，故有由此得距中性层为y 处的任一层纵向纤维的线应变ρy θρθρθy)(ρbb bb b'b'ε=-+=-=d d d (a) 上式表明，线应变ε?随y 按线性规律变化。
物理方面 根据单向受力假设，且材料在拉伸及压缩时的弹性模量E 相等，则由虎克定律，得ρy E E εσ== (b) 式(b)表明，纯弯曲时的正应力按线性规律变化，横截面上中性轴处，y =0，因而?=0，中性轴两侧，一侧受拉应力，另一侧受压应力，与中性轴距离相等各点的正应力数值相等（图7-5）。
静力学方面 虽然已经求得了由式(b)表示的正应力分布规律，但因曲率半径?和中性轴的位置尚未确定，所以不能用式(b)计算正应力，还必须由静力学关系来解决。
在图7-5中，取中性轴为z 轴，过z 、y 轴的交点并沿横截面外法线方向的轴为x 轴，作用于微面积dA 上的法向微内力为dA σ。
在整个横截面上，各微面积上的微内力构成一个空间平行力系。
由静力学关系可知，应满足0=∑x F ，0=∑y M ，0=∑z M 三个平衡方程。
由于所讨论的梁横截面上设有轴力，0=N F ，故由0=∑x F ，得0d ⎰==A N A σF (c) 将式(b)代人式(c)，得式中，E/??恒不为零，故必有静矩0d ⎰==Az A y S ，由第5章知道，只有当z 轴通过截面形心时，静矩S z 才等于零。
由此可得结论：中性轴z 通过横截面的形心。
这样就完全确定了中性轴在横截面上的位置。
由于所讨论的梁横截面上没有内力偶M y ，因此由0=∑y M ,得0d ⎰==A y A z σM (d) 将式(b)代人式(d)，得上式中，由于y 轴为对称轴，故0=yz I ，平衡方程0=∑z M 自然满足。
纯弯曲时各横截面上的弯矩M 均相等。
因此，由0=∑z M ，得⎰=A A y σM d (e)将式(b)代人式(e)，得 z A A I ρE A y ρE A ρy yE M ===⎰⎰d d 2 (f) 由式(f)得 zEI M ρ=1 （7-1） 式中，ρ1为中性层的曲率，EI z 为抗弯刚度，弯矩相同时，梁的抗弯刚度愈大，梁的曲率越小。
最后，将式(7-1)代入式(b)，导出横截面上的弯曲正应力公式为zI My σ= （7-2） 式中，M 为横截面上的弯矩，I z 为横截面对中性轴的惯性矩，y 为横截面上待求应力的y 坐标。
应用此公式时，也可将M 、y 均代入绝对值，σ是拉应力还是压应力可根据梁的变形情况直接判断。
以中性轴为界，梁的凸出一侧为拉应力，凹入一侧为压应力。
以上分析中，虽然把梁的横截面画成矩形，但在导出公式的过程中，并没有使用矩形的几何性质。
所以，只要梁横截面有一个对称轴，而且载荷作用于对称轴所在的纵向对称面内，式(7-1)和式(7-2)就适用。
由式(7-2)可见，横截面上的最大弯曲正应力发生在距中性轴最远的点上。
用y max 表示最远点至中性轴的距离，则最大弯曲正应力为上式可改写为z W M σ=max （7-3） 其中 m axy I W z z = （7-4） 为抗弯截面系数，是仅与截面形状及尺寸有关的几何量，量纲为[长度]3。
高度为h 、宽度为b 的矩形截面梁，其抗弯截面系数为直径为D 的圆形截面梁的抗弯截面系数为工程中常用的各种型钢，其抗弯截面系数可从附录的型钢表中查得。
当横截面对中性轴不对称时．其最大拉应力及最大压应力将不相等。
用式(7-3)计算最大拉应力时，可在式(7-4)中取y max 等于最大拉应力点至中性轴的距离；计算最大压应力时，在式(7-4)中应取y max 等于最大压应力点至中性轴的距离。
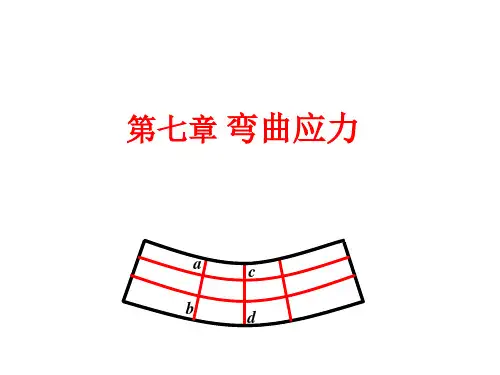
例7-1 受纯弯曲的空心圆截面梁如图7-6(a)所示。
已知：弯矩M = l ，外径D=50mm ，内径d =25mm 。
试求横截面上a 、b 、c 及d 四点的应力,并绘过a 、b 两点的直径线及过c 、d 两点弦线上各点的应力分布图。
解：（1） 求 I z（2） 求?a 点b 点c 点d 点给定的弯矩为正值，梁凹向上，故a 及c 点是压应力，而b 点是拉应力。
过a 、b 的直 径线及过c 、d 的弦线上的应力分布图如图7-6(b)、(c)所示。
横力弯曲梁的正应力公式（7-2）是纯弯曲情况下以7-2-1提出的两个假设为基础导出的。
工程上最常见的弯曲问题是横力弯曲。
在此情况下，梁的横截面上不仅有弯矩，而且有剪力。
由于剪力的影响，弯曲变形后，梁的横截面将不再保持为平面，即发生所谓的“翘曲”现象，如图7-7（a ）。
但当剪力为常量时，各横截面的翘曲情况完全相同，因而纵向纤维的伸长和缩短与纯弯曲时没有差异。
图7-7（b ）表示从变形后的横力弯曲梁上截取的微段，由图可见，截面翘曲后，任一层纵向纤维的弧长A ’B ’，与横截面保持平面时该层纤维的弧长完全相等，即A ’B ’=AB 。
所以，对于剪力为常量的横力弯曲，纯弯曲正应力公式(7-2)仍然适用。
当梁上作用有分布载荷，横截面上的剪力连续变化时，各横截面的翘曲情况有所不同。
此外，由于分布载荷的作用，使得平行于中性层的各层纤维之间存在挤压应力。
但理论分析结果表明，对于横力弯曲梁，当跨度与高度之比l ／h 大于5时，纯弯曲正应力计算公式(7-2)仍然是适用的，其结果能够满足工程精度要求。
例7-2 槽形截面梁如图7-8(a)所示，试求梁横截面上的最大拉应力。
解 绘M 图，得B 、C 两截面的弯矩kN.m 10-=B M ，kN.m 5.7=C M ,如图7-8(b)所示。
求截面的形心及对形心轴的惯性矩，取参考坐标z 1Oy ，如图7-8(c)所示，得截面形心C 的纵坐标因y 为对称轴，故过形心C 取z 轴，截面对z 轴的惯性矩为B 截面的最大拉应力为C 截面的最大拉应力为可见，梁的最大拉应力发生在C 截面的下部边缘线上。
弯曲切应力横力弯曲时，梁横截面上的内力除弯矩外还有剪力，因而在横截面上除正应力外还有切应力。
本节按梁截面的形状，分几种情况讨论弯曲切应力。
7.3.1 矩形截面梁的切应力在图7-9(a)所示矩形截面梁的任意截面上，剪力F Q 皆与截面的对称轴y 重合， 见图7-9(b)。
现分析横截面内距中性轴为y 处的某一横线，ss ’上的切应力分布情况。
根据切应力互等定理可知，在截面两侧边缘的s 和s ’处，切应力的方向一定与截面的侧边相切，即与剪力F Q 的方向一致。
而由对称关系知，横线中点处切应力的方向，也必然与剪力F Q 的方向相同。
因此可认为横线ss ’上各点处切应力都平行于剪力F Q 。
由以上分析，我们对切应力的分布规律做以下两点假设：1．横截面上各点切应力的方向均与剪力F Q 的方向平行。
2．切应力沿截面宽度均匀分布。
现以横截面m-m 和n-n 从图7-9(a)所示梁中取出长为d x 的微段，见图7-10(a)。
设作用于微段左、右两侧横截面上的剪力为F Q ，弯矩分别为M 和M +d M ，再用距中性层为y 的rs 截面取出一部分mnsr ，见图7-10 (b)。
该部分的左右两个侧面mr 和ns 上分别作用有由弯矩M 和M +d M 引起的正应力mr σ及ns σ。
除此之外，两个侧面上还作用有切应力τ。
根据切应力互等定理，截出部分顶面rs 上也作用有切应力'τ，其值与距中性层为y 处横截面上的切应力τ数值相等，见图7-10(b)、(c)。
设截出部分mnsr 的两个侧面mr 和ns 上的法向微内力mr σd A 和ns σd A 合成的在x 轴方向的法向内力分别为F N 1及F N 2，则F N 2可表示为*z zA z A z A ns N S I M M A y I M M A y I M M A σF d d d d d d 111112+=+=+==⎰⎰⎰ （a ） 同理 *z zN S I M F =1 （b ） 式中，A 1为截出部分mnsr 侧面ns 或mr 的面积，以下简称为部分面积*z S 为A 1对中性轴的静矩。
