2012中位数和众数第2课时

20.1.2中位数和众数教案（第二课时）一.教学目标1.知识与技能：通过本节课的学习进一步认识并掌握平均数、中位数和众数的计算方法；了解平均数、中位数、众数在描述数据时的差异。

2.过程与方法：经历例6的学习和探究过程，培养学生独立思考、表达交流的良好习惯和小组合作学习的能力。

3.情感、态度与价值观：通过真实且贴近生活的素材和问题情境，激发学生学习数学的热情和兴趣。

二．重点、难点以及突破难点的方法1.重点：了解平均数、中位数、众数之间的差异。

2.难点：灵活运用这三种数据代表解决问题。

3.突破难点的方法：先结合实际问题情境复习平均数、中位数和众数，再通过对例6的研究，让学生理解这三种数据代表的用处以及差异，从中体会并归纳三者各自的特点，最后辅助一定量的练习，加深理解和应用。

三．教学过程（一）创设情境，复习引入某商场服装部的王经理，为了调动营业员的积极性，他决定对平均月销售额最高的小组进行奖励，为此他打算对两个销售小组进行调查，统计了甲乙两个组的营业员在某个月的销售额（单位：万元），数据如下：甲组101010103050乙组171919191921思考:(1)整理数据后，王经理决定给甲组每位员工奖励1000元，你知道为什么吗？(2)乙组营业员得知甲组获奖励时,表示强烈不满,你能说说为什么吗?(3)对于以上奖励制度，如果你是其中一名员工，你对王经理有何建议？设计意图：结合具体情境，先复习平均数、中位数和众数，将这三者进行比较，认识到三者各自的适用特点。

（二）范例讲解王经理听取员工的建议后，他决定实行目标管理，对达到销售目标的营业员进行奖励. 为了确定一个适当的月销售目标，他统计了每个营业员在某个月的销售额（单位：万元），数据如下：17 18 16 13 24 15 28 26 18 1922 17 16 19 32 30 16 14 15 2615 32 23 17 15 15 28 28 16 19学生认真审题，教师讲解：确定一个适当的月销售目标是关键，如果目标定得太高，会使多数营业员完不成任务而打击信心，如果目标定得太低就不能发挥营业员的潜力。

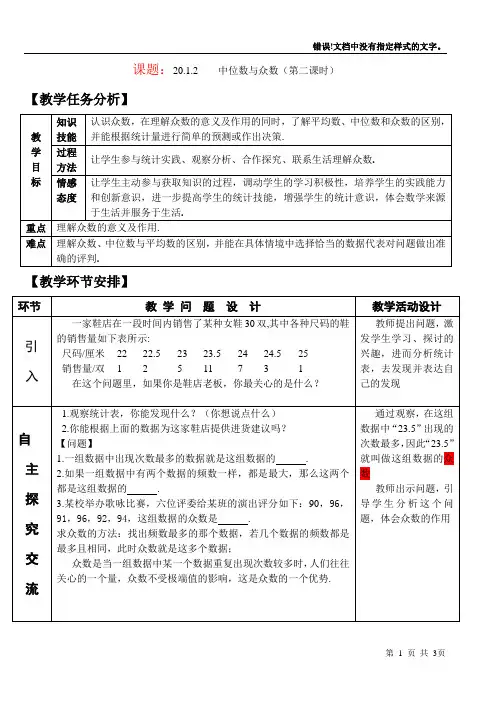
20.1.2 中位数和众数（第2课时）2016.6岳普湖县阿其克乡中学阿布都拉·艾尼瓦尔20.1.2 中位数和众数（第2课时）【教学目标】知识与能力1．认识众数，理解众数的意义，会求一组数据的众数；2．会利用众数分析数据信息做出决策；3．进一步认识众数是数据的代表；过程与方法能结合具体情境发现并提出数学问题，能把实际问题转化成数学问题，从不同角度寻求解决问题的方法，建立数学模型．情感态度与价值观1．培养认真、耐心、细致的学习态度和学习习惯；2．渗透数学知识来源于生活，反过来又服务于生活的思想；3．乐于接触数学信息，喜欢数学，敢于面对困难，有学好数学的自信心；4．在数学活动中体验到探索的乐趣和数学的魅力．【教学重点】认识众数数据代表；【教学难点】1、利用众数分析数据信息做出决策；2、灵活运用众数这个数据代表解决问题；【教学过程】（一）创设情境，导入新课一家童鞋店最近销售了某种童鞋30双，其中各种尺码的鞋的销售量如下表所示：如果你是鞋店老板，你最关心的是什么？（二）合作交流，探索问题例1 某鞋店在一段时间内销售了一批女鞋40双，其中各种尺码的销售量如下表所示：（1）计算40双女鞋尺寸的众数．（2）你能根据上面的数据为这家鞋店提供进货建议吗？解：（1）23.5是这组数据的众数．（2）由（1）得，23.5码的鞋销量最大，因此可以建议鞋店多进23.5码的鞋．众数在分析数据过程中充当了重要的角色，请同学们自学课本内容，明确中位数和众数的概念.学生自学课本内容学生口述概念众数：一组数据中出现次数最多的数称为这组数据的众数.（三）自主探究刚才我们从理论上把握住了众数的概念，那么怎样求一组数据的众数呢？请同学们自学课本内容后，完成问题2（课件出示）2．某商店3、4月份出售某一品牌各种规格的空调，销售台数如表所示：根据表格回答问题：商店出售的各种规格空调中，众数是多少？假如你是经理，现要进货，6月份在有限的资金下进货单位将如何决定？（1）1.2匹．（2）通过观察可知1.2匹的销售最大，所以要多进1.2匹，由于资金有限就要少进2匹空调．①学生独立完成②学生汇报，交流方法③师小结：求众数（先将数据从小到大（或大到小）排列，找出频数最多的那个数为众数，有一个取一个，有两个取两个，一个也没有就不取.（四）巩固练习（课件出示）1、对于数据组2、4、4、5、3、9、4、5、1、8，其众数是（）.2、一组数据23、27、20、18、ⅹ、12它的众数是27，则ⅹ的值是（）.3、如果在一组数据中23、25、28、22出现的次数依次为2、5、3、4，并且没有其它的数据，则这组数据的众数是（）.4、在一次英语口试中，10名学生的得分如下：80、70、90、100、80、60、80、70、90、100，则这次英语口试中，学生得分的众数是（）。

人教版义务教育课程标准教科书八年级下册20.1.2中位数和众数（第2课时）教学设计一、教材分析1、地位作用：在信息社会“数字”世界里，常常需要在不确定的情况下，根据大量纷繁复杂的数据做出一个合理的决策，而统计正是通过对数据的收集、整理和分析，为人们更好地制定决策提供依据及建议。

平均数，众数，中位数是描述一组数据的集中趋势的三个统计特征量，是帮助学生学会用数据说话的基本概念。

本节内容是进一步巩固平均数、众数和中位数的计算，并探究平均数、众数和中位数各自的特点，以及他们的联系，还有各自的适用范围。

本节课的内容对综合地合理分析数据有着重要作用。

2、教学目标：（1）进一步理解众数和中位数的含义，会熟练计算众数和中位数。

（2）了解平均数、中位数和众数各自的特点以及他们的联系，还有各自的适用范围，能够在解决问题时合理选用。

目标分析：教育家蒂斯多费曾经说过，如果使学生简单的接受和被动的工作，任何方法都是坏的，如果能激发学生的主动性，任何方法都是好的。

所以本节课关注学习者的自主学习和发展，选择贴近学生生活的素材和适当的问题情境，激发学生学习数学的热情和兴趣，让学生对学习材料进行数学化处理，启发学生利用已有知识计算、分析、比较等数学探究活动，体会平均数、众数、中位数三者的差别，了解平均数、中位数和众数各自的适用范围，并能够在解决具体问题时选择恰当的数据进行分析。

此外，让学生深刻体会到自主探索与合作交流是学习的重要方式。

3、教学重、难点重点：了解平均数、中位数和众数各自得特点、三者之间的联系，以及他们适用范围，并能够在解决问题时合理选用。

难点：体会平均数、众数、中位数三者的差别，并能在具体情境中选择恰当的数据代表对数据做出自己的评判。

突破方法：小组合作交流，师点拨讲解二、教学准备：多媒体课件、三角板、导学案三、教学过程。

20.1.2 中位数和众数第一课时教学目的1、认识中位数和众数，并会求出一组数据中的众数和中位数。

2、理解中位数和众数的意义和作用。

它们也是数据代表，可以反映一定的数据信息，帮助人们在实际问题中分析并做出决策。

3、会利用中位数、众数分析数据信息做出决策。

重点、难点和难点的突破方法1、重点：认识中位数、众数这两种数据代表2、难点：利用中位数、众数分析数据信息做出决策。

例习题的意图分析1、教材P143的例4的意图（1）、这个问题的研究对象是一个样本，主要是反映了统计学中常用到一种解决问题的方法：对于数据较多的研究对象，我们可以考察总体中的一个样本，然后由样本的研究结论去估计总体的情况。

（2）、这个例题另一个意图是交待了当数据个数为偶数时，中位数的求法和解题步骤。

（因为在前面有介绍中位数求法，这里不再重述）（3）、问题2显然反映学习中位数的意义：它可以估计一个数据占总体的相对位置，说明中位数是统计学中的一个重要的数据代表。

（4）、这个例题再一次体现了统计学知识与实际生活是紧密联系的，所以应鼓励学生学好这部分知识。

2、教材P145例5的意图（1）、通过例5应使学生明白通常对待销售问题我们要研究的是众数，它代表该型号的产品销售最好，以便给商家合理的建议。

（2）、例5也交待了众数的求法和解题步骤（由于求法在前面已介绍，这里不再重述）（3）、例5也反映了众数是数据代表的一种。

课堂引入严格的讲教材本节课没有引入的问题，而是在复习和延伸中位数的定义过程中拉开序幕的，本人很同意这种处理方式，教师可以一句话引入新课：前面已经和同学们研究过了平均数的这个数据代表。

它在分析数据过程中担当了重要的角色，今天我们来共同研究和认识数据代表中的新成员——中位数和众数，看看它们在分析数据过程中又起到怎样的作用。

例习题的分析教材P144例4，从所给的数据可以看到并没有按照从小到大（或从大到小）的顺序排列。

因此，首先应将数据重新排列，通过观察会发现共有12个数据，偶数个可以取中间的两个数据146、148，求其平均值，便可得这组数据的中位数。

第2课时中位数与众数教学目标【知识与技能】掌握中位数和众数的概念，并会求一组数据的中位数和众数.【过程与方法】通过结合具体情境，区别平均数、中位数和众数三者的差异，能初步选择恰当的数据代表对数据作出自己的评判.【情感态度】统计作为处理现实世界数据信息的一个重要数学分支，必然要求素材本身的真实性，以培养学生求真的科学态度；将知识的学习放在解决实际生活问题的情境中，使学生体会数学与现实的联系.【教学重点】求一组数据的中位数和众数.【教学难点】平均数、众数、中位数这三量之间的区别与联系.教学过程一、创设情境，导入新课小王大学毕业后到处寻找工作，某天他在报纸上看到了一条招聘广告：招聘启事我公司因扩大规模，现需招聘职员若干名.我公司员工收入高，月平均工资2000元.有意者请于×月×日到我公司面试.××公司人事部×年×月×日小王觉得这家公司的待遇还不错，于是就到这家公司进行面试，并被该公司聘用了.可是到公司上班两个月之后，他找到经理，说：“你们欺骗了我，我的工资才1 100元，而且我也问过其他职员，都没有得到过2 000元的.月平均工资怎么可能是2 000元？”而经理却不慌不忙的对小王说：“小王啊，不要这么激动嘛.我们公司的月平均工资确实是2 000元！这是我们公司的工资表，你自己看啊！”说着拿出了一张工资报表：000元？经理有没有欺骗小王呢？【教学说明】通过生活实例引起学生的探究兴趣，体会数学与生活的紧密联系，为后面的探究奠定基础. 二、合作探究，探索新知1.请同学们计算平均工资，并发表自己的看法.2.为什么月平均工资比他得到的工资高那么多呢？3.该公司的月平均工资能否客观地反映员工的工资收入？如果能，请说明理由；如果不能，那你认为哪个数据反映员工的工资收入比较合适呢？学生互相讨论，发表自己的看法.4.在小王询问其它职员的时候，职员C 说：“我的工资是1 200元，在公司算中等收入.”职员D 说：“我们好几个人的工资都是1 100元.”1 200元正好处在所有员工工资这组数据的“正中间”，我们称它为中位数.9个员工中有3个人的工资是1 100元，出现的次数最多，我们称它为众数.5.小结：中位数定义：一组数据按大小顺序排列，位于最中间的一个数据(当偶数个数据时，为最中间两个数据的平均数)叫做这组数据的中位数.众数定义：一组数据中，出现次数最多的数据叫做这组数据的众数.【教学说明】从实际例子的解答中总结中位数和众数的定义，使学生更容易理解概念.6.如何求一组数据的中位数和众数？应注意些什么？(1)求中位数要先把数据按大小顺序排列，可以从小到大，也可以从大到小.如果数据个数n 为奇数时，第n2个数据为中位数；如果数据个数n 为偶数时，第n 2、n2＋1个数据的平均数为中位数.(2)众数是数据中出现次数最多的数据，是一组数据中的原数据，而不是相应的次数.众数有可能不唯一，注意不要遗漏.(3)平均数、中位数和众数都是有单位的，和原数据的单位一致. 【教学说明】教师强调求中位数和众数应该注意的问题，使学生对中位数和众数的理解更深刻.三、示例讲解，下列方程：【例】某公司销售部有营销人员15人，销售部为了制定某种商品的销售金额，统计了这15个人的销售量如下(单位：件)1 800、510、250、250、210、250、210、210、150、210、150、120、120、210、150求这15个销售员该月销量的中位数和众数.假设销售部负责人把每位营销员的月销售定额定为320件，你认为合理吗？如果不合理，请你制定一个合理的销售金额并说明理由.解：(1)这15个销售员该月销量的中位数和众数分别为：210件、210件(2)不合理.因为15人中有13人的销售额达不到320件(320虽是原始数据的平均数，却不能反映营销人员的一般水平)，销售额定为210件合适，因为它既是中位数又是众数，是大部分人能达到的额定.【教学说明】教师可以先让学生独立思考，然后再进行讨论，最后教师再进行解答，重点关注学生对平均数、中位数和众数的理解.四、练习反馈，巩固提高1.数据8、9、9、8、10、8、9、9、8、10、7、9、9、8的中位数是__9__，众数是__9__.2. 一组数据23、27、20、18、X、12，它的中位数是21，则X 的值是22 .3.数据92、96、98、100、X的众数是96，则其中位数和平均数分别是(B)A.97、96B.96、96.4C.96、97D. 98、974.如果在一组数据中，23、25、28、22出现的次数依次为2、5、3、4次，并且没有其他的数据，则这组数据的众数和中位数分别是(C)A.24、25B.23、24C.25、25D. 23、255.(1)该组数据的中位数是什么？(2)若当气温在18℃～25℃为市民“满意温度”，则我市一年中达到市民“满意温度”的大约有多少天？解：(1)15(2)约97天五、师生互动，课堂小结1.什么是中位数和众数？2.怎样求一组数据的中位数与众数？要注意什么？课后作业完成同步练习册中本课时的练习.。

20.1.2 中位数和众数(第2课时)一、内容和内容解析1．内容平均数、中位数和众数的特点及其合理选择和运用．2．内容解析平均数、中位数和众数都可以作为一组数据的代表，用于描述一组数据的集中趋势，但描述的角度和适用范围有所不同，因此，在实际应用中，选择哪一个统计量来描述数据的集中趋势，需要综合考虑问题的具体情况、数据特征以及统计量的特点等．本节课的教学重点是：理解平均数、中位数和众数作为数据代表的意义，根据具体问题情境选择适当的统计量分析数据．二、目标和目标解析1．目标(1)在解决实际问题中进一步理解平均数、中位数、众数作为数据代表的意义，能根据所给信息求出相应的统计量．(2)能结合具体情境体会平均数、中位数、众数三者的特点与差异，能根据具体问题选择这些统计量来分析数据．(3)经历整理、描述、分析数据的过程，发展数据分析观念．2．目标解析目标(1)要求进一步理解数据代表的意义，并能在实际问题中计算相关的统计量．目标(2)要求能结合问题情境和数据特征，比较三个数据代表的特点与差异，选择适当的数据统计量分析数据．会综合运用不同的统计量，从多角度分析数据，获得信息．目标(3)是让学生充分体会各种统计量的统计意义，对选择适当的统计量解决问题、用样本估计总体以及数据处理的基本过程有进一步的认识．三、教学问题诊断分析通过前几节的学习，学生对平均数、中位数和众数有了一定的认识，而进一步体会三者的特点和差异以及如何根据解决问题的需要来选择合适的数据代表等，还需要综合考虑问题的具体情况、数据特征以及统计量的特点，学生会遇到较大困难．这需要通过对实际问题的分析和探讨，引导学生进一步感悟．本节课的教学难点是：能对具体问题进行分析，综合运用适当的统计量来多角度分析数据．四、教学过程设计1．复习巩固问题1请说说什么是平均数、中位数和众数？师生活动：回顾平均数、中位数和众数的相关知识，进一步明确它们的特点和意义．设计意图：综合回顾平均数、中位数和众数的意义．问题2有6户家庭的平均年收入(单元：万元)分别为：4，5，5，6，7，50，你认为这6户家庭的年收入水平大概是多少？师生活动：教师引导学生分别用平均数、中位数和众数估计6户家庭的年收入水平，再引导学生进行评价.(1)用平均数估计：45567506x＋＋＋＋＋＝≈12.83(万元)；(2)用中位数估计：中位数＝565＋＝5.5(万元)；(3)用众数估计：众数＝5(万元)．由于受极端数据影响，平均数与大多数家庭的实际年收入差距较大，用它来估计这6个家庭的年收入水平显然不太合适，中位数和众数比较贴近绝大多数家庭的实际，用它们描述数据的整体水平比较合适．设计意图：让学生体会在实际情境下用不同的统计量估计数据整体水平的合理性，初步体会三个统计量的不同特点．追问1：数据的特点怎样影响统计量描述数据集中趋势的合理性？师生活动：用图象呈现数据的变化，展现三个统计量与大多数数据的接近性变化过程，从而体会三个统计量的各自特点．设计意图：让学生通过图象直观感受平均数、中位数和众数的意义和特点．追问2：请说说平均数、中位数和众数的意义和特点．平均数计算要用到所有的数据，任何一个数据的变动都会相应引起平均数的变动，它能够充分利用所有的数据信息，但它受极端数据的影响较大．众数是当一组数据中某一数据重复出现较多时，人们往往关心的一个量，众数不受极端值的影响，这是它的一个优势，缺点是当众数有多个且众数的频数相对较小时可靠性小，局限性大．中位数仅与数据的排列位置有关，不易受极端数据影响，中位数可能出现在所给数据中也可能不在所给的数据中，当一组数据中的个别数据变动较大时，可用中位数描述其趋势，中位数的计算很少也不受极端值的影响．设计意图：回顾前面学习的平均数、中位数和众数知识，归纳各自的意义和特点，进一步理解这三个统计量的意义．追问3：还可以采用什么方法估计这6户家庭年收入水平？设计意图：引导学生开放性思考,培养创新意识．2．简单应用积累经验例题1八年级(1)班三位同学最近的五次数学测验成绩(单位：分)分别是：小华62 94 95 98 98小明62 62 98 99 100小丽40 62 85 99 99他们都认为自己的数学成绩比其他两位同学好，他们比较的依据分别是什么？师生活动：在教师指导下，让学生计算出三位同学成绩的平均数、中位数和众数，然后通过相互比较，找出三位同学的比较依据．设计意图：巩固平均数、中位数和众数的基础知识，体会平均数、中位数、众数三者的特点与差异，感受从不同的角度分析数据．追问：你认为谁的数学成绩最好呢？师生活动：让学生根据自己的理解和认识谈谈看法．设计意图：让有不同意见的同学阐述自己的看法和理由，通过比较鉴别来加深对具体问题如何选用数据代表的认识．3．综合应用，解决问题例题2 某商场服装部为了调动营业员的积极性，决定实行目标管理，根据目标完成的情况对营业员进行适当的奖励．为了确定一个适当的月销售目标，商场服装部统计了每个营业员在某月的销售额(单位：万元)，数据如下：17 18 16 13 24 15 28 26 18 1922 17 16 19 32 30 16 14 15 2615 32 23 17 15 15 28 28 16 19(1)月销售额在哪个值的人数最多？中间的月销售额是多少？平均的月销售额是多少？(2)如果想确定一个较高的销售目标，你认为月销售额定为多少合适？说明理由．(3)如果想让一半左右的人都能达到销售目标，你认为月销售额定为多少合适？说明理由．师生活动1：针对问题(1)，因样本共有30个数据，教师可以引导学生用图表来整理和描述数据，这样可以更快更直观地分析数据．师生活动2：针对问题(2)、(3)，教师要引导学生把销售目标衡量标准引向三个统计量，使学生能结合统计量来说明理由．设计意图：这是在学习过数据的收集、整理、描述与分析之后涉及到这四个环节的一个例题，为怎样综合运用已学的统计知识解决实际问题作了一个标准范例．当然，此例题的一个主要意图是区分平均数、众数和中位数这三个数据代表的异同．例题中(2)问和(3)问的不同，导致结果的不同，其目的是告诉学生应该根据题目具体要求来灵活运用三个数据代表解决问题．同时，使学生明确三种数据代表分别适用于怎样的问题情境．通过对本例题的研究，也客观的反映了数学知识对生活实践的指导有重要的意义，也体现了统计知识与生活实践是紧密联系的．4．小结教师与学生一起回顾本节课所学主要内容，并提出以下问题引导学生思考：(1)结合本节内容谈谈你对平均数、众数、中位数三者的特点和意义的认识．(2)在选择统计量时你有什么样的心得体会？(3)你有办法减少极端数据对平均数的影响吗？请举例说明．设计意图：用具体问题引导学生回顾和总结，深化对平均数、中位数、众数这三个统计量意义和特点的理解．作业：教科书第122页习题6、7．五、目标检测设计1．在一次环保知识竞赛中，某班50名学生成绩如下表所示：分别求出这些学生成绩的众数、中位数和平均数．设计意图：考核众数、中位数和平均数的计算．2．某射击运动员10次射击的得分如下：0，73，75，75，78，80，82，83，85，100.(1)分别求出这名运动员射击成绩的众数、中位数和平均数．(2)你认为应该使用众数、中位数和平均数中的哪一个来描述该运动员的射击成绩？设计意图：考核学生能否选择合适的数据代表描述数据特征．3．某高中实验班要在当地某初中选拔一名最具潜力的优秀射击运动员．经过五次测试(测试成绩为整数环)，发现王力、李枚、张杰的成绩非常突出．根据下表提供的数据，你觉得谁会被录取？说说你的理由．设计意图：考核学生在具体问题中选择适当数据代表分析数据的能力．4．某公司的33名职工的月工资(单位：元)如下：请根据以上工资表回答下列问题：(1)工资为多少元的人最多？中间的工资是多少元？平均工资是多少元？(2)你认为多少元的工资能更好的反映公司职工的月工资水平？说明理由．(3)总经理对大学刚毕业的应聘者说“我们公司的月平均工资是2 200元，希望你们加盟我们的公司且好好工作”．如果你是其中的一名应聘者，你将作何选择？谈谈你的看法．设计意图：问题(1)、(2)考查学生对众数、中位数和平均数在实际问题中的应用能力，是否明确三种数据代表分别适用于怎样的问题情境；问题(3)是一个开放的问题情境，让学生充分表达自己的观点，但要求学生言而有据，不能泛泛而谈．。

20.1.2 中位数和众数第2课时教学目标【知识与技能】描述众数的概念，会求一组数据的众数，能结合具体情境体会平均数、中位数、众数三者的区别，能初步选择恰当的数据代表对数据做出自己的评判.【过程与方法】通过实际背景，区分刻画“平均水平”的三个数据代表，形成获取数据、继续巩固对各种图表信息的识别与获取能力，养成对生活中所见到的统计图表进行数据处理和评判的主动意识.【情感态度】将知识的学习放在解决问题的情境中，作为数据处理过程的一部分，认识到数字与现实的联系.通过与同学间的交流合作，培养大家的合作精神.教学重难点【教学重点】了解平均数、中位数、众数之间的差异.【教学难点】灵活运用这三个数据代表解决问题.课前准备无教学过程一、情境导入，初步认识平均数、众数及中位数都是描述一组数据的集中趋势的特征数，但描述的角度和适用范围有所不同.二、典例精析，掌握新知例某商场服装部为了调动营业员的积极性，决定实行目标管理，即确定一个月销售目标，根据目标完成的情况对营业员进行适当的奖惩.为了确定一个适当的目标，商场统计了每个营业员在某月的销售额（单位：万元），数据如下：17 18 16 13 24 15 28 26 18 1922 17 16 19 32 30 16 14 15 2615 32 23 17 15 15 28 28 16 19（1）月销售额在哪个值的人数最多？中间的月销售额是多少？平均的月销额是多少？（2）如果想确定一个较高的销售目标，你认为月销售额定为多少合适？说明理由.（3）如果想让一半左右的营业员都能达到目标，你认为月销售额定为多少合适？说明理由.【分析】(1)中的目的是依次探讨月销售额的众数，中位数和平均数，为了便于解答，应对所给出的30个数据进行分析整理（如列出频数分布表或频数分布直方图）；（2）（3）小题则是选择平均数、中位数或众数来解决问题，这样可进一步认识用样本估计总体及数据处理.【教学说明】教师先予以分析，引导学生阅读理解题意，找出解决问题的方法，然后由学生自主探究，独立完成.教师巡视，及时引导学生利用频数分布表（或直方图）来找出数据的众数和中位数.对有困难的学生给予个别辅导.三、运用新知，深化理解教材P121练习【教学说明】通过练习，教师帮助学生分析，了解平均数、中位数和众数都可以作为一组数据的代表，它们有各自的特点.【答案】解：（1）第1组数据的平均数：（35+36+38+40+42+42+75）÷7＝44（kg）.众数是42kg，中位数是40kg.第2组数据的平均数：（35+36+38+40+42+42+45）÷7≈40（kg）.众数是42kg，中位数是40kg.（2）第1组数据的平均数大于第2组数据的平均数，众数和中位数相同.四、师生互动，课堂小结今天你有哪些收获？与同伴交流.课后作业1.布置作业：从教材“习题20.1”中选取.2.完成练习册中本课时练习.教学反思引导学生采用自主探索与合作交流的学习方式，力求做到让每一个学生都能参与探究，最终学会学习.。

中位数和众数第二课时教案3中位数和众数第二课时教案3一、教学目标：1、进一步认识平均数、众数、中位数都是数据的代表。

2、通过本节课的学习还应了解平均数、中位数、众数在描述数据时的差异。

3、能灵活应用这三个数据代表解决实际问题。

二、重点、难点和突破难点的方法1、重点：了解平均数、中位数、众数之间的差异。

2、难点：灵活运用这三个数据代表解决问题。

3、难点的突破方法：首先应复习平均数、众数和中位数的定义，将这三者进行比较，归纳三者的各自特点，以保证学生在应用过程中不致盲目乱用。

以下是这三个数据代表的异同。

平均数、中位数和众数都可以作为一组数据的代表，主要描述一组数据集中趋势的量。

平均数是应用较多的一种量。

另外要注意：平均数计算要用到所有的数据，它能够充分利用所有的数据信息，但它受极端值的影响较大.众数是当一组数据中某一数据重复出现较多时，人们往往关心的一个量，众数不受极端值的影响，这是它的一个优势，中位数的计算很少也不受极端值的影响.平均数的大小与一组数据中的每个数据均有关系，任何一个重要的意义，也体现了统计知识与生活实践是紧密联系的。

四、课堂引入：本节课的课堂引入可以通过复习平均数、中位数和众数定义开始，为完成重点、突破难点作好铺垫，没有必要牵强的加入一个生活实例作为引入问题。

五、例习题的分析：例题6中第一问是在巩固平均数定义、中位数定义和众数的定义。

可以引导学生从问题中词语特点分析它们分别指哪个数据代表，教师也可以顺便加一个发散性问题，一般地哪些词语是指平均数、中位数和众数呢?例题6中的第二问学生一般不易想到，教师要将较高目标衡量标准引向三个数据代表身上，这样学生就不难回答了。

第三问要抓住一半左右应与哪个数据代表的意义相符这个问题。

即要很好的回答第三问，学生头脑必须很清楚平均数、中位数、众数的特点。

六、随堂练习：1、在一次环保知识竞赛中，某班50名学生成绩如下表所示：得分5060708090100110120人数2361415541分别求出这些学生成绩的众数、中位数和平均数.2、公园里有甲、乙两群游客正在做团体游戏，两群游客的年龄如下：（单位：岁）甲群：13、13、14、15、15、15、16、17、17。