用迭代法求代数方程的近似根
- 格式:ppt
- 大小:159.50 KB
- 文档页数:13

使⽤“⽜顿迭代法”求解⽅程使⽤⽜顿迭代法求解⽅程尽管通过因式分解和利⽤求根公式可以很⽅便的得出多项式⽅程的根,但⼤多数时候这个多项式的次数都很⾼,计算将变得⾮常复杂,因此,我们必须转向⼀些近似解法。
⽜顿迭代法是其中最好的⽅法之⼀。
从根本上说,⽜顿迭代法通过⼀系列的迭代操作使得到的结果不断逼近⽅程的实根。
⾸先,要选择⼀个初始值x=x0,使得该初始值接近实根的值。
然后,迭代计算如下的公式:x i+1 = x i - f(x i) / f '(x i)直到x i+1达到⼀个满意的近似结果为⽌。
在这个公式中,f(x)是要求解的多项式⽅程,⽽f '(x)是f(x)的导数。
多项式求导多项式求导是微积分的基础,现在让我们来看看针对多项式求导的公式化描述。
要计算出多项式的求导结果,只需要对多项式的每⼀项套⽤如下两个公式:d/dx * k = 0, d/dx *kx r = krx r-1这⾥的k是为常数,r是有理数,x是未知数。
符号d/dx表⽰求导,其中x是多项式中的变量。
对于多项式中的每⼀常数项,套⽤第⼀个公式;否则,就⽤第⼆个公式。
假设有如下函数:f(x) = x3 + 5x2 +3x +4要得到求导后的结果f '(x),对该多项式的前三项套⽤第⼆个公式,最后⼀项套⽤第1个公式,得到结果如下:f '(x) = 1 * 3x(3-1) + 5 * 2x(2-1) + 3 * 1x(1-1) + 0 = 3x2 + 10x +3有时候也有必要进⾏⾼阶求导,即导数的导数。
⽐如,f(x)的2阶求导可记为f ''(x),它是对f '(x)的求导结果。
同理,f(x)的3阶求导可记为f'''(x),这是对f ''(x)的求导结果,以此类推。
因此,在前⾯的例⼦中,如果要计算f(x)的2阶导数的话,我们按照如下的⽅式对f '(x)求导即可:f ''(x) = 3 * 2x(2-1) + 10 * 1x(1-1) + 0 =6x +10理解1阶和2阶导数理解1阶和2阶导数的意义,是正确使⽤⽜顿迭代法⾮常重要的⼀点。

第二章 方程求根在许多实际问题中,常常会遇到方程f(x)=0求解的问题。
当f(x)为一次多项式时,f(x)=0称为线性方程,否则称为非线性方程。
对于非线性方程,由于f(x)的多样性,求其根尚无一般的解析方法可以使用,因此研究非线性方程的数值解法是十分必要的。
法、迭代法、牛顿法及割线法。
这些方法均是知道根的初始近似值后,进一步把根精确化,直到达到所要求的 精度为止。
也即求非线性方程根的数值方法。
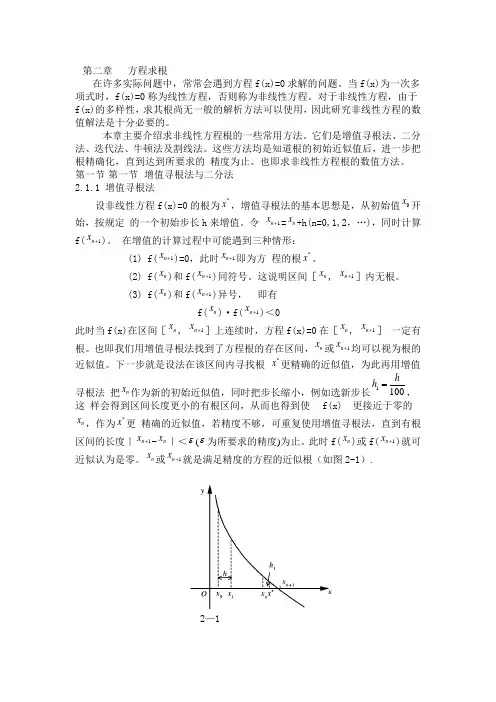
第一节 第一节 增值寻根法与二分法2.1.1 增值寻根法设非线性方程f(x)=0的根为*x ,增值寻根法的基本思想是,从初始值0x 开始,按规定 的一个初始步长h 来增值。
令 1n x +=n x +h(n=0,1,2,…),同时计算f(1n x +)。
在增值的计算过程中可能遇到三种情形:(1) f(1n x +)=0,此时1n x +即为方 程的根*x 。
(2) f(n x )和f(1n x +)同符号。
这说明区间[n x , 1n x +]内无根。
(3) f(n x )和f(1n x +)异号,f(n x )·f(1n x +)<0此时当f(x)在区间[n x , 1n x +]上连续时,方程f(x)=0在[n x , 1n x +] 一定有根。
也即我们用增值寻根法找到了方程根的存在区间,n x 或1n x +均可以视为根的近似值。
下一步就是设法在该区间内寻找根 *x 更精确的近似值,为此再用增值寻根法 把n x 作为新的初始近似值,同时把步长缩小,例如选新步长1100h h =,这 样会得到区间长度更小的有根区间,从而也得到使f(x)n x ,作为*x 更 精确的近似值,若精度不够,可重复使用增值寻根法,直到有根区间的长度|1n x +-n x |<ε(ε为所要求的精度)为止。
此时f(n x )或f(1n x +)就可近似认为是零。
n x 或1n x +就是满足精度的方程的近似根(如图2-1).2—1例1 用增值寻根法求方程f(x)=324x x +-10=0的有根区间。

数值分析实验(三)课题名称:利用四种方法求方程的根任课教师:辅导教师:专业班级:学号:姓名:实验编号:实验报告文件名:1.算法分析:求方程f(x)=x³-3*x-1=0的根。
1.对分区间法:f(x)在某一区间[a,b] 连续且端点出函数值异号,用中点的(a+b)/2平分区间,并计算处中点的函数值f((a+b)/2),若f(x)不等于0,每次改变区间范围。
具体步骤:1.找出f(x)=0的根的存在区间(a,b),并计算出端点的函数值f(a),f(b).2.计算f(x)在区间中点的值f((a+b)/2).3.判断:若f((a+b)/2)近似为0,则停止。
否则,若f((a+b)/2)与f(a)异号,则跟位于(a,(a+b)/2),以(a+b)/2代替b,若f((a+b)/2)与f(b)异号,则跟位于((a+b)/2,b),以(a+b)/2代替a。
4.重复(2)(3)步,直到区间缩小到容许的误差范围内,此时,区间中点可作为所求的根。
2.弦位法:用过两点的直线近似曲线,用直线与x轴的交点近似曲线与x轴的交点,需f(x)在零点附近的有连续的二阶微商。
具体步骤: 1.选定初始值a,b,并计算f(a),f(b)。
2. 迭代公式x[i]=a[i]-(f1/(f2-f1))*(b[i]-a[i]);再求f(x[i]);3.判断:若f(x[i])近似为0,则停止。
否则,若f(x[i])与f(a)异号,则跟位于(a,f(a))和(x[i],f(x[i])),代替(a,f(a))( b,f(b)),若f(x[i])与f(b)异号,则跟位于(x[i],f(x[i]))和(b,f(b)),代替(a,f(a))( b,f(b))。
4.重复(2)(3)步,直到相邻两次迭代值之差到容许的误差范围内,此时,所得的根。
3.迭代法:已知f(x),保留一个x在左边,右边写为g(x),强令左边x=x[k+1],右边是关于x[k]的函数g(x),给定初始值x,构造x的序列,若x收敛,g(x)连续,则x的收敛值为f(x)的值。

迭代法迭代法也称辗转法,是一种不断用变量的旧值递推新值的过程,跟迭代法相对应的是直接法(或者称为一次解法),即一次性解决问题。
迭代法又分为精确迭代和近似迭代。
“二分法”和“牛顿迭代法”属于近似迭代法。
迭代算法是用计算机解决问题的一种基本方法。
它利用计算机运算速度快、适合做重复性操作的特点,让计算机对一组指令(或一定步骤)进行重复执行,在每次执行这组指令(或这些步骤)时,都从变量的原值推出它的一个新值。
利用迭代算法解决问题,需要做好以下三个方面的工作:一、确定迭代变量。
在可以用迭代算法解决的问题中,至少存在一个直接或间接地不断由旧值递推出新值的变量,这个变量就是迭代变量。
二、建立迭代关系式。
所谓迭代关系式,指如何从变量的前一个值推出其下一个值的公式(或关系)。
迭代关系式的建立是解决迭代问题的关键,通常可以使用递推或倒推的方法来完成。
三、对迭代过程进行控制。
在什么时候结束迭代过程?这是编写迭代程序必须考虑的问题。
不能让迭代过程无休止地重复执行下去。
迭代过程的控制通常可分为两种情况:一种是所需的迭代次数是个确定的值,可以计算出来;另一种是所需的迭代次数无法确定。
对于前一种情况,可以构建一个固定次数的循环来实现对迭代过程的控制;对于后一种情况,需要进一步分析出用来结束迭代过程的条件。
例 1 :一个饲养场引进一只刚出生的新品种兔子,这种兔子从出生的下一个月开始,每月新生一只兔子,新生的兔子也如此繁殖。
如果所有的兔子都不死去,问到第12 个月时,该饲养场共有兔子多少只?分析:这是一个典型的递推问题。
我们不妨假设第 1 个月时兔子的只数为u 1 ,第 2 个月时兔子的只数为u 2 ,第 3 个月时兔子的只数为u 3 ,……根据题意,“这种兔子从出生的下一个月开始,每月新生一只兔子”,则有u 1 = 1 ,u 2 =u 1 +u 1 × 1 = 2 ,u 3 =u 2 +u 2 × 1 =4 ,……根据这个规律,可以归纳出下面的递推公式:u n =u n - 1 × 2 (n ≥ 2)对应u n 和u n - 1 ,定义两个迭代变量y 和x ,可将上面的递推公式转换成如下迭代关系:y=x*2x=y让计算机对这个迭代关系重复执行11 次,就可以算出第12 个月时的兔子数。

计算方法大作业学院:电子工程姓名:班级:学号:大作业选题:分析方程求根问题中牛顿法的性能,包括收敛性等,并用该方法求解一个问题,给出过程和结果。
一、牛顿迭代法介绍:用迭代法求方程0)(=x f 的根时,首先要构造一个迭代函数,迭代函数构造的好坏,不仅影响收敛速度,而且有可能使迭代序列发散,构造迭代函数的一条重要途径,是用近似方程代替原方程去求根,因此如果能将非线性方程0)(=x f 用线性方程来近似代替,那么求近似根问题就容易得到解决,而且十分方便。
牛顿法就是把非线性方程线性化的一种方法。
二、牛顿迭代法原理设已知方程0)(=x f 的近似根0x ,则在0x 附近)(x f 可用一阶泰勒多项式))((')()(000x x x f x f x p -+=近似代替.因此, 方程0)(=x f 可近似地表示为0)(=x p .用1x 表示0)(=x p 的根,它与0)(=x f 的根差异不大.设0)('0≠x f ,由于1x 满足,0))((')(0100=-+x x x f x f 解得)(')(0001x f x f x x -= 重复这一过程,得到迭代公式)(')(1n n n n x f x f x x -=+ 这就是著名的牛顿迭代公式,它相应的不动点方程为)(')()(x f x f x x g -=.用牛顿迭代公式求方程根的方法称为牛顿迭代法,简称牛顿法。
三、牛顿迭代法的几何解析在0x 处作曲线的切线,切线方程为))((')(000x x x f x f y -+=。
令0=y ,可得切线与x 轴的交点坐标)(')(0001x f x f x x -=,这就是牛顿法的迭代公式。
因此,牛顿法又称“切线法”,其几何意义即为0x 点处的切线方程。
四、牛顿迭代法的收敛性 计算可得2)]('[)(")()('x f x f x f x g -=,设*x 是0)(=x f 的单根,有0)(',0)(**≠=x f x f ,则0)]('[)(")()('2****=-=x f x f x f x g , 故在*x 附近,有1)('<x g .根据不动点原理知牛顿迭代法对单根收敛.同理可知当*x 是0)(=x f 的重根时也收敛,则可分析出牛顿法不论对单根还是重根均是局部收敛的,只要初值足够靠近*x ,牛顿迭代序列均收敛于*x 。

牛顿迭代法是一种近似求解方程根的方法,它通过不断迭代逼近解的过程来求解方程在某一点附近的根。
在本文中,我将共享关于牛顿迭代法求解方程在1.5附近的根的全面评估和深度探讨。
通过逐步分析牛顿迭代法的原理和具体应用,希望能够帮助您更深入地理解这一方法的优势和局限性。
一、牛顿迭代法的原理牛顿迭代法的基本原理是利用函数的导数来不断逼近方程的根。
具体来说,对于方程f(x)=0,从一个初始值x0开始,通过不断迭代x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}来逼近方程的根,直到满足所需精度要求为止。
这一迭代过程可以通过图形直观理解:在函数图像上,从初始点开始,沿着切线逐步逼近根的过程。
二、牛顿迭代法的应用牛顿迭代法在实际问题中有着广泛的应用,尤其是在科学计算和工程领域。
通过牛顿迭代法可以求解非线性方程、优化问题和曲线拟合等,在实际工程中有着重要的价值。
在求解方程根的问题中,牛顿迭代法通常能够以较快的速度逼近准确解,尤其是在靠近初始点附近的情况下,具有更佳的收敛速度。
三、牛顿迭代法的局限性然而,牛顿迭代法并不是没有局限性的。
在某些情况下,由于函数导数的特殊性或初始点选择不当,牛顿迭代法可能出现迭代不收敛或者收敛速度较慢的情况,这时需要对迭代方法进行调整或选择其他方法来求解方程的根。
在实际应用中,需要综合考虑问题的特点和要求,选择合适的数值方法来求解方程根。
四、牛顿迭代法求解方程在1.5附近的根接下来,我们将以求解方程f(x)=x^3-4x^2+1在x=1.5附近的根为例,来演示牛顿迭代法的具体应用过程。
我们需要确定方程f(x)=x^3-4x^2+1的导数f'(x)=3x^2-8x。
选择一个合适的初始点x0=1.5,代入牛顿迭代公式x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}中,进行迭代计算直到满足精度要求。
通过反复迭代计算,最终得到方程在1.5附近的根为x=2.532。



牛顿迭代法的应用一、牛顿法简介牛顿迭代法(Newton's method )又称为牛顿-拉夫逊方法(Newton-Raphson method ),它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。
多数方程不存在求根公式,因此求精确根非常困难,甚至不可能,从而寻找方程的近似根就显得特别重要。
牛顿迭代法是求方程根的重要方法之一,其最大优点是在方程f(x) = 0的单根附近具有平方收敛,而且该法还可以用来求方程的重根、复根,此时线性收敛,但是可通过一些方法变成超线性收敛。
该方法广泛用于计算机编程中。
简单迭代法是用直接的方法从原方程中隐含地解出x ,从而确定出)(x ϕ。
而牛顿迭代法是用一种间接而特殊的方法来确定)(x ϕ的。
下面具体推到牛顿迭代公式。
假设k x 是非线性方程为0)(=x f 的一个近似根,把)(x f 在k x 处作泰勒展开:+-+-+=2''')(!2)())(()()(k k k k k x x x f x x x f x f x f若取前两项来近似代替)(x f (称为)(x f 的线性化),则得近似的线性方程0))(()()('=-+≈k k k x x x f x f x f设0)('≠k x f ,令其解为1+k x ,则得)()('1k k k k x f x f x x -=+ (1)这称为0)(=x f 的牛顿迭代公式。
它对应的迭代方程为)()('x f x f x x -=显然是0)(=x f 的同解方程,故其迭代函数为)()()('k k k x f x f x x -=ϕ (0)('≠x f ) 在0)(=x f 的根α的某个邻域)|(|δα≤-x R 内,0)(≈x f1|)('||)(||)(||)(|2'''<≤•=L x f x f x f x ϕ 在α的邻域R 内,对任意初值x 0,应用由公式(1)来解方程的方法称为牛顿迭代法,它是解代数方程和超越方程的有效方法之一。

习题二3、证明:当X 0=1.5时,迭代法X k+1=Xk +410和X k+1=21k X 310-都收敛于方程f(x)=x 3+4x 2-10=0在区间[1,2]内唯一实根x *,并分别用上述迭代法求满足于精度要求︱X k+1-X k ︱≤10-5的近似根。
解:证明:{先用迭代法求f(x)=x 3+4x 2-10=0的根。
(a )对x 3+4x 2-10=0变形有:4x 2=10-x 3所以:X=21310X - 则相应的迭代公式为:X k+1=21k X 310- 取:X 0=1.5,根据计算可以看出看,我们认为得到的迭代序列是收敛的。
}(此行可忽略){ 由 f(x)=x 3+4x 2-10=0得迭代方程:X=21310X -=g (x ) 先证明在区间【1,2】上x=g (x )有实根。
由于[1,2]上g ‘(x )存在,所以g (x )连续。
作Q (x )=x-g(x),则Q(x)在[1,2]上也连续。
由定理1条件2有:Q (1)=1-g (1)≤0,Q (,2)=1-g (2)≥0故存在x *∈[1,2]使Q *(x )=0,即x *= Q *(x )又因为,x *是方程f(x)=x 3+4x 2-10=0在区间[1,2]内的唯一实根,(由定理一条件2)对任意的x 0∈[1,2]时,X k ∈[1,2](k=0,1,2,3…)因为:x *- X k+1=g (x *)-g (X k )=g ‘(h k )(x *- X k )故由条件1知:︱X *-X k+1︱≤L ︱X *-X k ︱(k=0,1,2,3…)于是有:0≤︱X *-X k ︱≤L k ︱X *-X 0︱,0<L <1,立即可知:lim (k 趋于无穷)︱X *-X k ︱=0,从而lim (k 趋于无穷)X k= X *。
所以当X 0=1.5时,迭代法X k+1=Xk +410和X k+1=21k X 310-都是由迭代法X k+1=g (X k )产生的迭代序列{ X k }收敛于方程f(x)=x 3+4x 2-10=0在区间[1,2]内唯一实根x *。
Python 迭代法求解方程本文介绍了使用 Python 编写迭代法求解方程的程序,并举例说明了如何使用迭代法求解一元二次方程、指数方程和三角方程。
下面是本店铺为大家精心编写的5篇《Python 迭代法求解方程》,供大家借鉴与参考,希望对大家有所帮助。
《Python 迭代法求解方程》篇1引言迭代法是一种常用的数值计算方法,用于求解各种方程。
在Python 中,可以使用迭代法来求解各种方程,例如一元二次方程、指数方程和三角方程等。
本文将介绍如何使用 Python 编写迭代法求解方程的程序,并举例说明如何使用迭代法求解不同类型的方程。
一、一元二次方程一元二次方程的一般形式为:$$x^2+bx+c=0$$其中,$a,b,c$为常数,$x$为未知数。
使用迭代法求解一元二次方程的步骤如下:1. 选择一个初始值$x_0$。
2. 计算下一次的值$x_{n+1}$。
$$x_{n+1}=frac{x_n^2+bx_n+c}{x_n+b}$$3. 重复步骤 2,直到$x_n$满足精度要求。
下面是一个使用 Python 求解一元二次方程的程序:```pythondef quadratic(a, b, c, x0, tolerance):x = x0while abs(x - x0) > tolerance:x0 = xx = (x**2 + b*x + c) / (x + b)return x```其中,$a, b, c, x0$为输入参数,$tolerance$为精度要求。
二、指数方程指数方程的一般形式为:$$a^x=b$$其中,$a,b$为常数,$x$为未知数。
使用迭代法求解指数方程的步骤如下:1. 选择一个初始值$x_0$。
2. 计算下一次的值$x_{n+1}$。
$$x_{n+1}=frac{1}{2}(x_n+frac{b}{a^{x_n}})$$3. 重复步骤 2,直到$x_n$满足精度要求。
```pythondef exponent(a, b, x0, tolerance):x = x0while abs(x - x0) > tolerance:x0 = xx = 0.5 * (x + b / a**x)return x```其中,$a, b, x0$为输入参数,$tolerance$为精度要求。
用迭代法与牛顿法求近似值摘要:本文给出了相当广泛的一类方程求解的近似值的方法,高次方程,()x x ϕ=方程,线性方程,以及迭代函数的估值等方面,举例作了说明. 关键词:迭代法;牛顿法;对角占优矩阵Finding the approximation by the iterative method andNewton’s methodAbstract: In this paper are given the methods to find the approximate value of a solution of rather general a kind of equations, and given some examples to explainthese methods on the estimation of,equation of higher degree equation,()x x ϕ=,linear equation, and iterative functionKeywords : iterative method; Newton’s method,;domination diagonally matrix.1引言迭代思想是现代数学中的一个重要思想,在数学的一些分支领域中人们常采用迭代法来逼近某问题的解,取得了重要的成果.古希腊天文学家托勒密(Peolemy )的方法,首开使用迭代法之先河;迭代法最先在牛顿(New.ton)那里成为体系,解决了多项式函数()f x 和超越函数的近似解;数学家皮卡(Picard)也曾利用迭代法解决了常微分方程理论中重要的具有奠基意义的一阶微分方程解的存在唯一性定理.到近现代,迭代研究更是方兴未艾,被称为现代数学之灵的分形几何理论大展迭代之奇妙魅力,人们将其从实数系转至复数系,开拓了解析映照迭代(复动力系统)的研究视野,使目前最新的物理学理论奇异吸引子、混沌理论研究大有推[1]动.利用这种思想解决一些基本的数学问题,其内容也是相当丰富的,本文利用迭代法仅就狭义的意义来谈的,它是求解相当广的一类方程的一个很有效的方法.可以用迭代对精确解进行逐步逼近.已知方程()0f x =的一个近似根后,通常使用某个固定公式反复校正根的近似值,使之逐步精确化,一直到满足给定的精确度要求为止.具体作法是,把给定方程()0f x =改写成等价形式()x x ϕ=. (1) 在根*x 的附近任取一点0x 作为*x 的预测值,把0x 代入式(1)的右端,计算得到1x =0()x ϕ.一般说来10x x ≠(如果()x x ϕ=,10x x =,则*1x x =),再把1x 作为根*x 的新的预测值代入式(1)得21()x x ϕ=.重复上述步骤,则有如下迭代公式1()k k x x ϕ+= 0,1,2,k =L (2)其中()x ϕ称为迭代函数,并有如下迭代序列. 01,,k x x x L L如果迭代序列{}k x 的极限存在,则称迭代过程收敛,显然有 *x lim k k x →∞=.如果迭代序列{}k x 的极限不存在,则称迭代过程发散.定理1.([2]中定理1) 若∀[,]x a b ∈有()a x b ϕ≤≤,且存在正数1L <使得|()|1x L ϕ'≤<. (3) 则迭代过程1()k k x x ϕ+=对于任意初值0[,]x a b ∈均收敛于方程()x x ϕ=的根*x .定理2.([2]中定理2) 设()x ϕ在方程()x x ϕ=根*x 的附近有连续的一阶导数且|()|1x ϕ'<则迭代过程1()k k x x ϕ+=具有局部收敛性.2的近似值首先我们假设已求出的1x ,用1α来表示1x 的误差,即假设11()k x a α+=.根据牛顿二项公式我们有111111()k k k x x kx αα-+=++L 这个等式可以写成下面的形式1111k k x kx a α-++=L .若所选择的初始近似值1x,则这个近似值的误差1α很小,因此可以舍去含有2311,ααL 的项.这样我们就得到:1111k k x kx a α-+≈.由这个近似等式推出1111kk a x kx α--≈. 因此可以取数11211111(1)k kk k a x a k x x x kx kx ---+-=+=的下一近似值.一般地,的近似值n x ,则下一近似值由公式11(1)kn n k na k x x kx +-+-= (4) 确定.当n x 与1n x +在给定的精确度的范围内相同时,就应停止计算,并取这个相同值作为所求的[3]值. 例2.10.001.解.由公式(4)知,取1x =3 则有52438043 3.33853x +⨯==⨯,534544553804 3.338 3.283,5 3.3383804 3.331 3.281,5 3.3313804 3.329 3.281,5 3.329x x x +⨯==⨯+⨯==⨯+⨯==⨯我们看到,在给定的精确度范围内,4x 与5x 一样,所以我们有3解高次方程设一般的代数方程为101()0n n n f x a x a x a -=+++=L .假设我们用某种方法求出了这个方程的根的第一近似值1x ,它的误差为1α,于是我们有11()0f x α+=,因为()f x α+的展开式可写为()()()f x f x f x αα'+=++L ,所以111()()0f x f x α'++=L . (5)若第一近似值选择的好,则它的误差1α很小,这时方程(5)中的省略号表示的那些项也很小.舍去这些项,我们得到确定1α的近似等式111()()0f x f x α'+≈.由此推出得111()()f x f x α≈-'. 因此根的第二近似值2x ,由公式1211()()f x x x f x =-'给出,一般地,若已求出根的某一近似值n x ,则下一近似值由公式1()()n n n n f x x x f x +=-'. (6) 若在给定精确度的范围内,近似值n x 与1n x +相同,则我们的计算已完成. 例3.1 取0 1.5x =作为第一近似值解方程310x x --=精确到0.0001. 解:因为多项式3()1f x x x =--的导数为2()31f x x '=-. 所以公式(6)为312131n n n n n x x x x x +--=-- 因此当0 1.5x =时31231121211.5 1.511.5 1.3572,3 1.5111.3309,31x x x x x x --=-=⨯---=-=-经过7次迭代,结果如下表nn x0 1 2 3 4 5 6 7 1.5 1.3572 1.3309 1.3259 1.3249 1.3248 1.3247 1.3247从表可以看到在给定的精确度范围内,7x 与6x 完全相同,因此可以说1.3247为所求的根.上面介绍的方法称为牛顿法.在用上述方法解题时,根的初始值的选择有决定意义,一些初始值得到一些根,另一些初始值得到另一些根,而有一些初始值算出的数列12,,,n x x x L 不趋于任何确定的值,是一个发散的数列. 具体初值的选取,只要它满足引言中的定理1和定理2即可.4解形如()x x ϕ=的方程在引言中,我们已推导出()x x ϕ=的迭代函数,迭代公式,以及收敛性,知道其迭代公式为1()k k x x ϕ+=,0,1,2,k =L . 下面我们举个例子具体的看一下它的解法. 例4.1求方程 cos sin 4x xx +=(7) 的解,精确到0.0001. 解:因为sin cos ()4x xx ϕ-+'=,但|sin |1x ≤,|cos |1x ≤, 所以|sin cos ||sin ||cos |1|()|1442x x x x x ϕ-++'=≤≤<,满足定理2,因而可用迭代法.选择某一近似值.例如10x =,并将它代入等式(7)的右边得到值 2cos0sin 010.2544x +===, 取作所求根的第二近似值,将2x 代入(7)式的右边,得到第三近似值. 3cos0.25sin 0.250.96890.24730.304144x ++===.依次计算得:40.3134x =, 50.3149x =,60.3152x =,70.3152x =.我们看到,在要求的精确度范围内,有6x 与7x 相等.因此0.3152为所求的根.5解线性方程组上面解的都是一元方程,现在我们来解线性方程组. Ax b = 假设已给n 个元n 的一次方程。
3.⽜顿迭代法求解⽅程的根⽜顿迭代法求解⽅程的根引题:⽤⽜顿迭代法求下列⽅程在值等于x 附近的根:2x 3−4x 2+3x −6=02x3−4x2+3x −6=0输⼊:输⼊x 。
输出:⽅程在值等于x 附近的根,占1⾏。
输⼊⽰例:1.5输出实例:21. ⽜顿迭代公式推导设多项式f (x )f(x),设r 是f (x )f(x)的根。
选取x 0x0作为r 的初始近似值。
过点x 0,f x 0(x0,f(x0))做曲线y =f (x )y =f(x)的切线L 。
得L :y =f x 0+f ′x 0x −x 0y =f(x0)+f ′(x0)(x −x0)则L 与x 轴交点的横坐标为 x 1=x 0−f x 0f ′x 0x1=x0−f ′(x0)f(x0),那么称x 1x1为r 的⼀次近似值。
过点x 1,f x 1(x1,f(x1))做曲线y =f (x )y =f(x)的切线,并求该切线与x 轴交点的横坐标x 2=x 1−f x 1f ′x 1x2=x1−f ′(x1)f(x1),称x 2x2为r 的⼆次近似值。
重复以上过程,得r 的近似值序列。
其中,x n +1=x n −f x n f ′x nxn+1=xn −f ′(xn )f(xn )称为r 的n+1次近似值。
所以,x n +1=x n −f x n f ′x nxn+1=xn −f ′(xn )f(xn )即为⽜顿迭代公式。
2. ⽜顿迭代公式核⼼思想核⼼思想:使⽤泰勒级数的线性项近似计算函数f (x )=0f(x)=0的根。
把f (x )f(x)在点x 0x0的某领域内展开成泰勒级数,取其线性部分(即泰勒展开的前两项),并令其等于0。
泰勒级数展开式:f x =f x 0+f ′x 0x −x 0+f ′′x 0x −x 0)22!+…+f (n )x 0x −x 0)n n !+R n x f(x)=f(x0)+f ′(x0)(x −x0)+2!f ′′(x0)(x−x0)2+…+n!f(n)(x0)(x−x0)n +Rn (x)线性部分:f x =f x 0+f ′x 0x −x 0f(x)=f(x0)+f ′(x0)(x −x0)令其为0,并以此作为⾮线性⽅程f (x )=0f(x)=0的近似⽅程,即切线⽅程,得到公式:x =x 0−f (x )f ′x x =x0−f ′(x)f(x)将其推⼴,即可以得到⽜顿迭代公式:x n +1=x n −f x n f ′x n xn+1=xn −f ′(xn )f(xn )#include <iostream>#include <cmath>using namespace std;double f(double x)//函数{return 2*pow(x,3)-4*pow(x,2)+3*x-6;}double f1(double x)//导函数{return 6*pow(x,2)-8*x+3;}(())()()()()()(())()()()()()()()()()()()(()(()()()()()()()()int main(){float x;cin >> x;do{x = x - f(x)/f1(x);}while( f(x)>1e-5 || f(x)<-(1e+5) );//控制精度,逼近处理cout << x << endl;}Loading [MathJax]/jax/output/HTML-CSS/fonts/TeX/fontdata.js。
(实用版4篇)编写:_______________审核:_______________审批:_______________单位:_______________时间:_______________序言本店铺为大家精心编写了4篇《牛顿迭代法解一元多次方程的方法》,供大家借鉴与参考。
下载后,可根据实际需要进行调整和使用,希望对大家有所帮助。
(4篇)《牛顿迭代法解一元多次方程的方法》篇1牛顿迭代法是一种求解一元多次方程近似根的数值方法。
它基于泰勒公式的近似,通过不断迭代,逐步逼近方程的根。
具体步骤如下:1. 初始化:给定一元多次方程 ax^n+bx^(n-1)+cx^(n-2)+...+zx+d=0,选取一个初始值 x0,并设置一个误差限额 e。
2. 计算函数值:计算函数 f(x) = ax^n+bx^(n-1)+cx^(n-2)+...+zx+d 在x0 处的值,即 f(x0) = a*x0^n+b*x0^(n-1)+c*x0^(n-2)+...+z*x0+d。
3. 计算导数:计算函数 f(x) 在 x0 处的导数,即 f"(x0) =n*a*x0^(n-1)+(n-1)*b*x0^(n-2)+(n-2)*c*x0^(n-3)+...+z。
4. 更新解:利用牛顿迭代公式 x_{n+1} = x_n - f(x_n)/f"(x_n),计算出下一次迭代的解 x_{n+1}。
5. 判断收敛:比较 x_{n+1} 与 x_n 之间的误差,如果小于等于 e,则认为已经收敛,输出结果;否则,回到第 4 步,继续迭代,直到误差小于等于 e。
需要注意的是,牛顿迭代法仅适用于一元多次方程,且要求方程的系数是常数。
《牛顿迭代法解一元多次方程的方法》篇2牛顿迭代法是一种求解一元多次方程近似根的方法,它是从泰勒公式中取前两项构成线性近似方程,然后通过迭代逐步逼近精确解。
下面是使用牛顿迭代法解一元多次方程的一般步骤:1. 根据方程的系数和常数项,写出方程的泰勒公式。