第 讲 捷联惯导系统 Allan方差

allan方差法原理
Allan方差法是一种用于分析时间序列数据的方法，尤其在分析MEMS（微电子机械系统）的随机误差时被广泛应用。

其基本原理如下：
1. 设系统采样周期为τ，连续采样N个数据点Y(i)，i=1，2，3…N。

2. 对任意的时间r=mτ，m=1,2…N/2，计算该组时间内各点的均值序列
Y(K)。

3. 由式D(K)=Y(K+M)-Y(K)求取差值序列D(K)，其中K=1,2…N-2M+1。

4. 普通Allan方差的定义如式σ=1，2，⋯，Round((N/m)-1)，其中表示取均值。

5. Allan方差反映了相邻两个采样段内平均频率差的起伏。

它的最大优点在于对各类噪声的幂律谱项都是收敛的；此外每组测量N一2，大大缩短了测量的时间。

6. 交叠式Allan方差由式(4)计算：(τ)=1/2 P=1,2…N-2M+1。

如需更多信息，建议阅读统计学相关书籍或请教统计学专业人士。

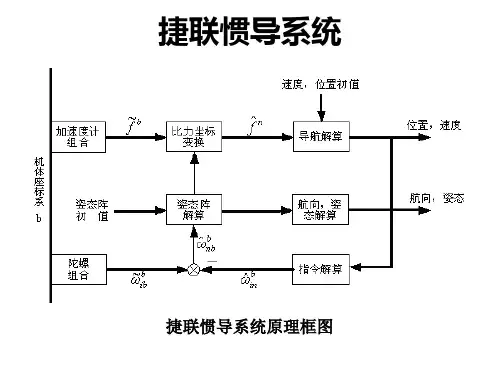
捷联惯导算法与组合导航原理讲义一、捷联惯导算法捷联惯导（Inertial Navigation System，INS）是一种通过测量惯性传感器的运动参数实现导航定位的技术。

惯性导航系统中包括了加速度计和陀螺仪等传感器，通过测量物体的加速度和角速度，可以推算出物体的位置、速度和姿态等信息。

1.1加速度计加速度计是一种测量物体加速度的传感器。

常见的加速度计有基于压电效应的传感器和基于微机电系统（Microelectromechanical System，MEMS）的传感器。

加速度计的原理是通过测量物体受到的惯性力，推算出物体的加速度。

由于加速度是速度对时间的导数，因此通过对加速度的积分操作，可以计算出物体的速度和位移。

1.2陀螺仪陀螺仪是一种测量物体角速度的传感器。

常见的陀螺仪有机械陀螺仪和MEMS陀螺仪等。

陀螺仪的原理是基于角动量守恒定律，通过测量转动惯量的变化，推算出物体的角速度。

与加速度计类似，通过对角速度的积分操作，可以计算物体的姿态。

1.3捷联惯导算法离散时间模型中，位置、速度和姿态等状态变量通过积分加速度和角速度来更新。

由于加速度计和陀螺仪测量结果存在噪声，因此在积分操作时需要加入误差补偿算法来消除误差。

常见的误差补偿算法有零偏校正和比例积分修正等。

连续时间模型中，位置、速度和姿态等状态变量通过微分方程来描述，并通过求解微分方程来更新状态。

由于计算量较大，通常需要使用数值积分方法来求解微分方程。

常见的数值积分方法有欧拉法、中点法和四阶龙格-库塔法等。

二、组合导航原理组合导航是一种融合多种导航技术的导航方式。

常见的组合导航方式有捷联惯导与GPS组合导航。

组合导航通过融合多种导航系统的测量结果，可以提高导航定位的精度和可靠性。

2.1捷联惯导与GPS组合导航捷联惯导与GPS组合导航是一种常见的组合导航方式。

在这种方式下，捷联惯导提供了高频率的惯导数据，可以提供较高的定位精度，但是由于其测量结果累积误差较大，会逐渐偏离真实轨迹。

捷联惯导系统 的关键问题捷联系统的导航任务关键问题（光学陀螺捷联惯导系统）： （一）惯性器件误差的分析与补偿1．随机误差2．温度漂移误差（二）初始对准初始对准的任务是确定捷联矩阵的初始值。

初始对准的误差将会对捷联惯导系统的工作造成难以消除的影响，导致对准误差的主要因素：1．惯性器件误差；2．干扰运动。

因此，滤波技术对捷联系统尤为重要。

（三）姿态解算中的动态误差补偿高频动态环境下，必须补偿如下的整流误差：1．圆锥误差（姿态误差）2．划船误差（速度误差）3．涡卷误差（位置误差）第一部分惯性器件误差的 分析与补偿1．光学陀螺的数学模型与主要性能指标 1.1 光学陀螺的工作原理Sagnac环形干涉仪1.2 数学模型与性能指标由IEEE 标准给出的光学陀螺输入输出模型为160]101][[)/(−−+++=∆∆K D E I t N S ε （1-1）式中：为标称的标度因子，单位：（角秒/脉冲数）；0S /P "t N ∆∆/为输出脉冲速率，单位：（脉冲数/秒）； s /P I 为输入角速度，单位：（角秒/秒）；s /"E 为环境敏感误差，主要由温度变化引起，单位：； s /"D 为漂移误差，单位：；s /"k ε为标度因子误差，单位：。

ppm 表征光学陀螺的主要性能指标有标度因数、零偏、零漂、随机游走系数，其中后三项用于描述光学陀螺输出中的漂移误差。

标度因数：陀螺仪输出量与输入角速度的比值，通常取/P′′（脉冲数/角秒）的量纲。

零偏：是当输入角速度为零时陀螺仪的输出，以规定时间内测得的输出量平均值相应的等效输入角速度表示，习惯上取（度/小时）的量纲。

h/o零漂：又称为零偏稳定性。

通常，静态情况下光学陀螺长时间稳态输出是一个平稳随机过程，即稳态输出将围绕零偏起伏和波动，表示这种起伏和波动的标准差被定义为零漂，其单位用表示。

h/o随机游走系数：由白噪声产生的随时间积累的输出误差系数，其量纲为h/o，它反映了光学陀螺输出随机噪声的强度。

捷联惯导系统从20世纪60年代初开始发展起来，在1969年，捷联惯导系统作为"阿波罗"-13号登月飞船的应急备份装置，在其服务舱发生爆炸时将飞船成功地引导到返回地球的轨道上时起到了决定性作用，成为捷联式惯导系统发展中的一个里程碑。

捷联式惯性导航(strap-downinertialnavigation)，捷联（strap-down）的英语原义是“捆绑”的意思。

因此捷联式惯性导航也就是将惯性测量元件（陀螺仪和加速度计）直接装在导弹需要诸如姿态、速度、航向等导航信息的主体上，用计算机把测量信号变换为导航参数的一种导航技术。

一、捷联惯导系统工作原理及特点惯导系统基本工作原理是以牛顿力学定律为基础，通过测量载体在惯性参考系的加速度，将它对时间进行积分，之后将其变换到导航坐标系，得到在导航坐标系中的速度、偏航角和位置信息等。

捷联惯导系统（SINS）是一种无框架系统，由三个速率陀螺、三个线加速度计和微型计算机组成。

由于惯性元器件有固定漂移率，会造成导航误差，因此导弹通常采用指令、GPS或其组合等方式对惯导进行定时修正，以获取持续准确的位置参数。

如采用指令+捷联式惯导捷联惯导系统能精确提供载体的姿态、地速、经纬度等导航参数，是利用惯性敏感器、基准方向及最初的位置信息来确定运载体的方位、位置和速度的自主式航位推算导航系统。

在工作时不依赖外界信息，也不向外界辐射能量，不易受到干扰破坏。

它完全是依靠载体自身设备独立自主地进行导航，它与外界不发生任何光、声、磁、电的联系，从而实现了与外界条件隔绝的假想的“封闭”空间内实现精确导航。

所以它具有隐蔽性好，工作不受气象条件和人为的外界干扰等一系列的优点。

除此以外捷联惯导系统的最大特点是没有实体平台，即将陀螺仪和加速度计直接安装在机动载体上，在计算机中实时的计算姿态矩阵，通过姿态矩阵把导航加速度计测量的载体沿机体坐标系轴向的加速度信息变换到导航坐标系，然后进行导航计算。

《现代导航测试技术》实验报告实验名称：光纤陀螺随机误差的Allan方差分析法班级：0309103学号：**************时间：2012-12-17一：实验目的由于光学陀螺的工作原理和环境干扰等原因，在光学陀螺输出信号中包含很多确定性和随机性的误差项。

光学陀螺的随机误差主要包括量化噪声、角速度随机游走、零偏不稳定性】角速率随机游走、速度斜坡和正弦分量，其中前三项误差被认为是其光学性能指标一部分。

对于这些随机误差，利用常规的分析方法，例如计算机样本均值和方差并不能揭示潜在的误差源，另一方面，虽然自相关函数和功率谱密度函数分别从时域和频域描述了随机误差的统计特性，但是在实际工作中通过这些函数加以分析将随机误差分离出来是很困难的。

Allan 方差法是20世纪60年代由美国国家标准局David Allan 提出的，它是一种基于时域的分析方法，不仅可以用来分析光学陀螺的误差特性，而且还可以应用于其他任何精密测量仪器.Allan 方差法的主要特点是能非常容易对各种误差源及其对整个噪声统计特性的贡献进行细致的表征和辨识，而且便于计算，易于分离。

它提供了一种识别并量化存在于数据中的不同噪声项。

二：实验原理与实验内容1.Allan 方差定义与计算设以采样时间τ0对陀螺仪输出角速率进行采样，共采样N 个点，把所获得的N 个数据分成K ，每组包含M 个采样点。

K=N/M ，M ≤（N-1）/2如图：ω1，ω2，…，ωM ωM+1，ωM+2，…，ω2M ωN-M+1，ωN-M+2，…，ωNK=1 k=2 k=K 每一组的持续时间τM =M τ0，称之为相关时间，每一组的平均值为ωk （M ）=(1)11Mk M ii Mω-+=∑ k=1,2,3,…,KAllan 方差定义为:221211111()(()())(()())22(1)K k k k k A M k M M M M k ωστωωωω-++=≡<->=--∑ 2．Allan 方差法最大的优点是可以简便细化分离、辨识光学陀螺的各项误差，同时确定各个误差项对总误差的贡献。

捷联惯性导航系统算法
1.经典捷联惯性导航算法(毕卡逼近、旋转矢量、四阶龙格库塔算法)，使用C语言编写，在
实际的系统中得到验证；
2.组合导航算法，包括：速度匹配、位置匹配、姿态角匹配等；
3.捷联惯性导航系统初始对准算法，粗对准方法：经典解析法、基于惯性系抗晃动基座解析
法，精对准方法：基于Kalman滤波的速度匹配、位置匹配精对准方法；
4.捷联惯导系统姿态算法研究，包括：四阶龙格库塔算法、旋转矢量算法，在典型圆锥运动
环境下对姿态解算算法系数进行优化；
5.利用Allan方差分析对光纤陀螺随机误差进行分析，为了抑制随机误差采用Kalman滤波
器对其进行滤波；
6.单轴旋转捷联惯导系统(SINS)多位置初始对准算法以及导航解算方法；
以上所有算法均采用C语言编写，且已经在实际的惯性导航系统中进行了充分的验证，如果需要交流，可以进一步进行联系！。

allan方差allan 方差（阿伦方差）是David AIlan于1966年提出的，最初该方法是用于分析振荡器的相位和频率不稳定性，高稳定度振荡器的频率稳定度的时域表征目前均采用Allan方差。

由于陀螺等惯性传感器本身也具有振荡器的特征，因此该方法随后被广泛应用于各种惯性传感器的随机误差辨识中。

中文名allan方差外文名allan variance属性物理计算方法提出人David Allan提出时间1966年1. 阿伦方差的定义，计算方法以及物理意义。

David AIlan于1966年提出了Allan方差,最初该方法是用于分析振荡器的相位和频率不稳定性，高稳定度振荡器的频率稳定度的时域表征目前均采用Allan方差。

由于陀螺等惯性传感器本身也具有振荡器的特征，因此该方法随后被广泛应用于各种惯性传感器的随机误差辨识中。

Allan方差的基本原理如下：设系统采样周期为τ，连续采样N个数据点.Y(i)，i=1，2，3…N。

对任意的时间r=mτ，m=1,2…N/2,由式(1)求该组时间内各点的均值序列Y(K),由式(2)求取差值序列D(K).Y(K)=1/M K=1,2…N-M+1 (1)D(K)=Y(K+M)-Y(K) K=1,2…N-2M+1 (2)普通AlIan方差的定义如式(3)。

其中<>表示取均值，σ=1，2，⋯，Round((N/m)-1)。

(τ)=1/2<D((P-1)M+1)>(3)Allan方差反映了相邻两个采样段内平均频率差的起伏。

它的最大优点在于对各类噪声的幂律谱项都是收敛的；此外每组测量N一2，大大缩短了测量的时间。

交叠式Allan方差由式(4)计算：(τ)=1/2<D(P)2> P=1,2…N-2M+1 (4)衡量陀螺精度的一个非常重要的指标是陀螺随机漂移(drift)，又指偏置稳定性(bias stabil—ity)以及零偏稳定性，不同应用场合对陀螺的漂移精度提出不同的要求。

allan方差allan方差allan 方差（阿伦方差）是David AIlan于1966年提出的，最初该方法是用于分析振荡器的相位和频率不稳定性，高稳定度振荡器的频率稳定度的时域表征目前均采用Allan方差。

由于陀螺等惯性传感器本身也具有振荡器的特征，因此该方法随后被广泛应用于各种惯性传感器的随机误差辨识中。

中文名allan方差外文名allan variance属性物理计算方法提出人David Allan提出时间1966年1. 阿伦方差的定义，计算方法以及物理意义。

David AIlan于1966年提出了Allan方差,最初该方法是用于分析振荡器的相位和频率不稳定性，高稳定度振荡器的频率稳定度的时域表征目前均采用Allan方差。

由于陀螺等惯性传感器本身也具有振荡器的特征，因此该方法随后被广泛应用于各种惯性传感器的随机误差辨识中。

Allan方差的基本原理如下：设系统采样周期为τ，连续采样N个数据点.Y(i)，i=1，2，3…N。

对任意的时间r=mτ，m=1,2…N/2,由式(1)求该组时间内各点的均值序列Y(K),由式(2)求取差值序列D(K).Y(K)=1/M K=1,2…N-M+1 (1)D(K)=Y(K+M)-Y(K) K=1,2…N-2M+1 (2)普通AlIan方差的定义如式(3)。

其中<>表示取均值，σ=1，2，?，Round((N/m)-1)。

(τ)=1/2(3)Allan方差反映了相邻两个采样段内平均频率差的起伏。

它的最大优点在于对各类噪声的幂律谱项都是收敛的；此外每组测量N一2，大大缩短了测量的时间。

交叠式Allan方差由式(4)计算：(τ)=1/2 P=1,2…N-2M+1 (4)衡量陀螺精度的一个非常重要的指标是陀螺随机漂移(drift)，又指偏置稳定性(bias stabil—ity)以及零偏稳定性，不同应用场合对陀螺的漂移精度提出不同的要求。

MEMS的随机误差具有慢时变、非平稳的特点，因而对其的辨识更适合采用Allan方差分析法。