第五章：竖曲线设计

纵断面设计——竖曲线设计纵断面上相邻两条纵坡线相交的转折处，为了行车平顺用一段曲线来缓和，这条连接两纵坡线的曲线叫竖曲线。

竖曲线的形状，通常采用平曲线或二次抛物线两种。

在设计和计算上为方便一般采用二次抛物线形式。

纵断面上相邻两条纵坡线相交形成转坡点，其相交角用转坡角表示。

当竖曲线转坡点在曲线上方时为凸形竖曲线，反之为凹形竖曲线。

一、竖曲线如图所示，设相邻两纵坡坡度分别为i1 和i2，则相邻两坡度的代数差即转坡角为ω= i1-i2 ，其中i1、i2为本身之值，当上坡时取正值，下坡时取负值。

当i1- i2为正值时，则为凸形竖曲线。

当i1 - i2 为负值时，则为凹形竖曲线。

（一）竖曲线基本方程式我国采用的是二次抛物线形作为竖曲线的常用形式。

其基本方程为：若取抛物线参数为竖曲线的半径，则有：（二）竖曲线要素计算公式竖曲线计算图示1、切线上任意点与竖曲线间的竖距通过推导可得：2、竖曲线曲线长：L = Rω3、竖曲线切线长：T= TA =TB ≈ L/2 =4、竖曲线的外距：E =⑤竖曲线上任意点至相应切线的距离：式中：x —为竖曲任意点至竖曲线起点（终点）的距离, m；R—为竖曲线的半径，m。

二、竖曲线的最小半径(一)竖曲线最小半径的确定1.凸形竖曲线极限最小半径确定考虑因素（1）缓和冲击汽车行驶在竖曲线上时，产生径向离心力，使汽车在凸形竖曲线上重量减小，所以确定竖曲线半径时，对离心力要加以控制。

（2）经行时间不宜过短当竖曲线两端直线坡段的坡度差很小时，即使竖曲线半径较大，竖曲线长度也有可能较短，此时汽车在竖曲线段倏忽而过，冲击增大，乘客不适；从视觉上考虑也会感到线形突然转折。

因此，汽车在凸形竖曲线上行驶的时间不能太短，通常控制汽车在凸形竖曲线上行驶时间不得小于3秒钟。

（3）满足视距的要求汽车行驶在凸形竖曲线上，如果竖曲线半径太小，会阻挡司机的视线。

为了行车安全，对凸形竖曲线的最小半径和最小长度应加以限制。

竖曲线讲解Vertical Curve ExplanationA vertical curve is a geometric design element used in road and highway engineering to provide a smooth transition between two different grades or elevations. It ensures a comfortable and safe driving experience by gradually changing the slope of the road, reducing the impact on vehicles and passengers.竖曲线是道路和公路工程中使用的几何设计元素，用于在两个不同的坡度或高程之间提供平滑过渡。

它通过逐渐改变道路的坡度，确保舒适和安全的驾驶体验，减少对车辆和乘客的冲击。

There are two types of vertical curves: sag curves and crest curves. Sag curves are concave downward, resembling the shape of a valley, and are used when the road descends from a higher elevation to a lower one. On the other hand, crest curves are convex upward, resembling the shape of a hill, and are employed when the road ascends from a lower elevation to a higher one.竖曲线分为两种类型：凹曲线和凸曲线。

凹曲线向下凹，形似山谷，用于道路从较高高程降至较低高程的情况。

第五章站场平、纵断面及排水第二节进出站疏解线路和站线的平、纵断面一、进出站疏解线路和站线的平面进出站疏解线路的曲线半径1 、进出站疏解线路的平面应符合相邻区段正线的规定。

在困难条件下，进出站疏解线路的最小曲线半径不应小于300m ；编组站环到、环发线的最小曲线半径不应小于250m 。

进出站疏解线路因与区间线路直接连接，为使客、货列车保持正常运行，故其平面设计应与所衔接的正线规定一致。

但位于枢纽范围内的车站的进出站线路，大多在城市附近，列车进出站速度较低。

因此，在困难条件下，为避免引起大量工程，减少用地和拆迁，其线路最小曲线半径可采用300m 。

编组站的环到、环发线只运行货物列车，进出站速度较低，在困难条件下，为了减少用地、拆迁和工程量，可采用不小于250m 的曲线半径。

2 、编组站各车场应设在直线上。

在特别困难条件下，到达场、到发场和出发场可设在同向曲线上，其曲线半径不应小于800m 。

编组站由到达场、到发场、出发场、调车场和编发场等车场组成，各种作业复杂而量大。

为改善运营条件，提高作业效率，要求编组站各车场应设在直线上。

如果条件困难，为了节省工程量，可允许利用咽喉区的道岔布置及其连接曲线，在车场咽喉部分设置较小的转角以适应地形的需要，但在线路有效长度范围内，仍应保持直线。

在特别困难条件下，如有充分依据，允许将到达场、出发场和到发场设在曲线上，其曲线半径不应小于800m 。

但调车场不得设在曲线上，因为设在曲线上的调车场影响车辆溜放。

3 、货物装卸线应设在直线上。

在困难条件下，可设在半径不小于600m 的曲线上；在特别困难条件下，曲线半径不应小于500m 。

货物装卸线如设在小半径曲线上时，由于车辆距站台的空隙较大，装卸不便，又不安全；同时，相邻车辆的车钩中心线相互错开，车辆的摘挂作业困难。

因此，货物装卸线应设在直线上；在困难条件下，可设在半径不小于600m 的曲线上，在特别困难条件下，曲线半径不应小于500m4 、牵出线应设在直线上。

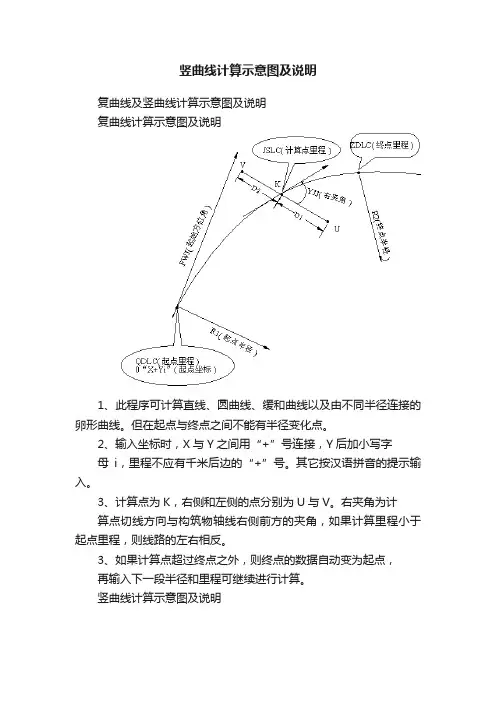
竖曲线计算示意图及说明
复曲线及竖曲线计算示意图及说明
复曲线计算示意图及说明
1、此程序可计算直线、圆曲线、缓和曲线以及由不同半径连接的卵形曲线。

但在起点与终点之间不能有半径变化点。

2、输入坐标时，X与Y之间用“+”号连接，Y后加小写字
母i，里程不应有千米后边的“+”号。

其它按汉语拼音的提示输入。

3、计算点为K，右侧和左侧的点分别为U与V。

右夹角为计
算点切线方向与构筑物轴线右侧前方的夹角，如果计算里程小于起点里程，则线路的左右相反。

3、如果计算点超过终点之外，则终点的数据自动变为起点，
再输入下一段半径和里程可继续进行计算。

竖曲线计算示意图及说明
1、竖曲线只能计算两个变坡点之间的高程。

按上图中所示的汉语拼音提示输入数据。

2、如果计算里程超过终点里程，则终点自动变为起点，然后再按提示输入下一个变坡点的数据，继续进行计算。

纵断面上相邻两条纵坡线相交的转折处，为了行车平顺用一段曲线来缓和，称为竖曲线。

在纵坡设计时．由于纵断面上只反映水平距离和竖直高度，因此竖曲线的切线长与弧长是其在水平面上的投影，切线支距是竖直的高程差，相邻两条纵坡线相交角用转坡角表示。

当竖曲线转坡点在曲线上方时为凸形竖曲线，反之为凹形竖曲线：一、竖曲线要素计算公式如图1-3-6所示，设转坡处相邻两纵坡度分别为i1和i2，转坡角以w表示，则转坡角w为式中符号意义同前。

从以上两种情况的计算公式可知，式(1-3-12)计算结果明显大于式(1-3-10)，因此是凸形竖曲线上满足视距要求的计算公式。

(二)按行程时间求竖曲线最小长度和半径汽车从直坡段驶入竖曲线时，当竖曲线的转坡角很小，即使半径较大，如果其竖曲线长度过短，汽车倏忽而过，冲击力大，旅客会感到不舒适，太短的竖曲线长度从视觉上也会感到线形突然转折。

因此，应限制汽车在竖曲线上的行程时间不宜过短．以此来控制竖曲线的最小长度和半径，即式中：v——计算行车速度，km/h；t——汽车在竖曲线上行程时间，一般取t＝3s。

(三)按径向离心力求坚曲线最小长度和半径汽车在竖曲线上行驶时，产生径向离心力。

这个力在凸形竖曲线上是减少重力．在凹形竖曲线上是增加重力，如果这种离心力达到某种程度时，旅客就会有不舒适的感觉，同时对汽车的悬挂系统也有不利影响。

因此，应对径向离心力加以控制。

汽车在竖曲线上行驶时其径向离心力为式中：F——径向离心力，N；G——汽车的总重力，N；g——重力加速度，m/s2；V—计算行车速度，km/h；v——车速，m/s；R——竖曲线半径，m。

为保证车辆在竖曲线上行驶的安全和舒适，根据试验得知，一般应将F/G控制在0.025以内，则得竖曲线最小半径为：根据汽车在凸形竖曲线上行驶的视距要求，行程时间及径向离心力三种影响因素，分别计算出凸形竖曲线的最小长度和半径，取其中较大者作为确定依据。

各级公路的竖曲线最小长度和半径规定如表l-3-9所示。

竖曲线计算公式步骤嘿，朋友们！今天咱来聊聊竖曲线计算公式步骤。

你说这竖曲线啊，就像是道路上的小魔术，能让我们的行车变得更平稳、更安全呢！先来说说竖曲线是啥玩意儿。

它呀，其实就是在道路纵断面上，为了缓和行车时的颠簸，而设计的那一段曲线。

想象一下，要是没有它，那车子开起来得多颠啊，就跟坐过山车似的，那可受不了！那怎么计算竖曲线呢？别急，听我慢慢道来。

首先，得搞清楚竖曲线的几个关键参数，比如变坡点的高程啦，前后坡的坡度啦。

这就好比做菜得先准备好食材一样，这些参数就是我们计算的基础呢。

然后呢，根据这些参数，我们就能套用公式啦。

这公式啊，就像是一把神奇的钥匙，能打开竖曲线的秘密大门。

通过一系列的计算，我们就能得出竖曲线的各种数据，比如曲线的长度啦，切线的长度啦。

哎呀，你说这是不是很有意思？就像解开一道谜题一样，一步一步地找到答案。

不过可别小瞧了这些步骤哦，要是算错了一点点，那竖曲线可就不完美啦，到时候行车可就没那么舒服咯！比如说，在计算的时候，要是把坡度给弄错了，那后果不堪设想啊！就好比你走路的时候，本来以为是平路，结果一脚踩空，那多吓人呀！所以啊，我们得仔仔细细地算，不能有一丝马虎。

还有啊，在实际应用中，我们还得考虑很多其他的因素呢。

比如地形啦，车辆的行驶速度啦。

这就像是给竖曲线穿上一件合适的衣服，让它更合身，更能发挥作用。

你想想看，要是在一个陡峭的山坡上，竖曲线就得设计得更平缓一些，不然车子怎么能开得上去呢？要是在一条平坦的道路上，竖曲线就可以稍微简单一点啦。

总之呢，竖曲线计算公式步骤虽然看起来有点复杂，但只要我们认真去学，去理解，就一定能掌握它。

就像学骑自行车一样，一开始可能会摔倒，但多练几次，不就会了嘛！所以啊，朋友们，别害怕这些公式和步骤，它们可是我们道路设计的好帮手呢！让我们一起把竖曲线算得妥妥的，让道路变得更美好吧！哈哈！。

竖曲线设计1、 竖曲线设计的一般要求竖曲线是否平顺，在视觉上往往是构成纵断面线形优劣的主要原因。

纵断面线形不好的原因大多数是由设置过多的竖曲线和竖曲线长度小或竖曲线半径小引起的。

所以，竖曲线设计时应遵循以下一般原则和要求。

（1） 宜选用较大的竖曲线半径竖曲线设计，首先应确定合适的半径，在不过分增加工程量的情况下，尽可能选用较大的竖曲线半径。

特别是前后两相邻纵坡的代数差小时，竖曲线更应采取大半径，以利于视觉和路容美观。

只有当地形限制或其他特殊困难在不得已时才允许采用极限最小半径。

在有条件路段，为获得平顺而连续的线形，并通视良好时，可参阅下表的规定选择竖曲线半径。

从视觉观点所需的竖曲线最小半径同向竖曲线，特别是同向凹形竖曲线间如直线段不长，应合并为单曲线或复曲线。

（3） 反向曲线间，一般由直线段连接，亦可相互直接连接反向竖曲线间，最好中间设置一段直线段，直线段长度一般不小于计算行车速度行驶3s 的行程长度，以使汽车从失重（或增重）过渡到增重（或失重）有一个缓和段。

如受条件限制也可相互直接连续，或插入短直线。

（4） 竖曲线设置应满足排水需要若相邻纵坡之代数差很小时，采用大半径竖曲线可能导致竖曲线上的纵坡小于0.3％，这样不利于排水，应重新设计，以避免这种情况。

2、 半径的选择竖曲线半径的选择主要考虑的因素有：1） 选择半径应符合规范定的竖曲线最小长度要求。

2） 在不过分增加土石方工程数量的情况下，为使行车舒适，应采用较大的半径。

3） 结合纵断面起伏情况和标高控制要求，确定合适的外距值，按外距控制半径，计算公式如下28ωER =4） 考虑相邻竖曲线的连接（即保证最小直坡段长度或不发生重叠）限制曲线长度，按切线长度选择半径。

如ωTR 2=5） 过大的竖曲线半径将使竖曲线过长，从施工和排水来看都是不利的，选择半径时应注意。

6） 夜间行车交通量较大的路段考虑灯光照射方向的改变，使前灯照射范围受到限制，选择半径时应适当加大，以使其有较长的照射距离。

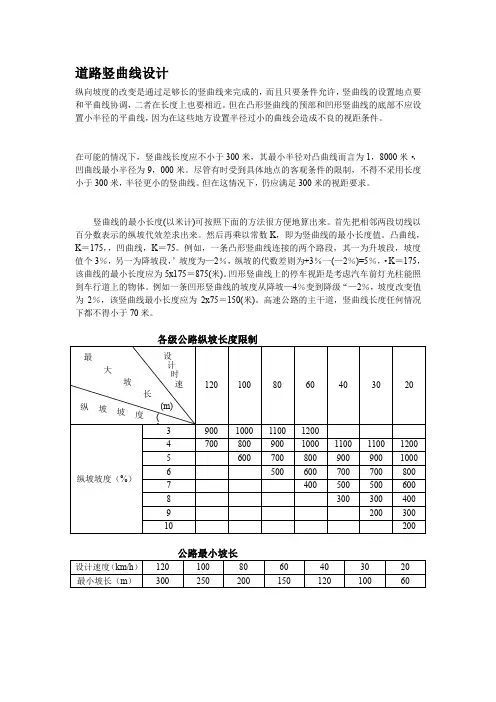
道路竖曲线设计纵向坡度的改变是通过足够长的竖曲线来完成的，而且只要条件允许，竖曲线的设置地点要和平曲线协调，二者在长度上也要相近。

但在凸形竖曲线的预部和凹形竖曲线的底部不应设置小半径的平曲线，因为在这些地方设置半径过小的曲线会造成不良的视距条件。

在可能的情况下，竖曲线长度应不小于300米，其最小半径对凸曲线而言为1，8000米·，凹曲线最小半径为9，000米。

尽管有时受到具体地点的客观条件的限制，不得不采用长度小于300米，半径更小的竖曲线。

但在这情况下，仍应满足300米的视距要求。

竖曲线的最小长度(以米计)可按照下面的方法很方便地算出来。

首先把相邻两段切线以百分数表示的纵坡代效差求出来。

然后再乘以常数K，即为竖曲线的最小长度值。

凸曲线，K＝175，，凹曲线，K＝75。

例如，一条凸形竖曲线连接的两个路段，其一为升坡段，坡度值个3％，另一为降坡段，’坡度为—2％，纵坡的代数差则为+3％一(—2％)=5％，·K＝175，该曲线的最小长度应为5x175＝875(米)。

凹形竖曲线上的停车视距是考虑汽车前灯光柱能照到车行道上的物体。

例如一条凹形竖曲线的坡度从降坡—4％变到降级“—2％，坡度改变值为2％，该竖曲线最小长度应为2x75＝150(米)。

高速公路的主干道，竖曲线长度任何情况下都不得小于70米。

下面是经典古文名句赏析！！不需要的朋友，可以下载后编辑删除！！谢谢经典古文名篇（一）；1.陋室铭刘禹锡（唐）字梦得《刘梦得文集》；山不在高，有仙则名；2．马说韩愈（唐）字退之《昌黎先生集》；世有伯乐，然后有千里马；马之千里者，一食(shí)或尽粟一石（dàn）；策之不以其道，食(sì)之不能尽其材（才），鸣之；3．师说韩愈（唐）；古之学者必有师；嗟乎！师道之不传也久矣！欲人之无惑也难矣！古之圣；圣人无常师；李氏子蟠，年十七经典古文名篇（一）1. 陋室铭刘禹锡（唐）字梦得《刘梦得文集》山不在高，有仙则名。

公路勘测设计竖曲线设计的课后反思一、引言公路勘测设计是公路工程中的重要环节，而竖曲线设计作为其中的关键内容之一，更是对公路安全和舒适度有着直接影响的部分。

在学习和实践中，我对公路勘测设计竖曲线设计有了一些新的认识和感悟，特此进行课后反思和总结。

二、深度评估1. 对公路勘测设计竖曲线设计的理解竖曲线设计是指在纵向地形变化较为显著的区段进行设计时，考虑车辆行驶舒适性和安全性的设计。

在实际的勘测设计中，需要充分考虑地形、车辆行驶速度、视距等因素，合理设置竖曲线的形状和参数，以保证车辆行驶的安全和舒适度。

2. 全面评估竖曲线设计的影响因素竖曲线设计是受到多种因素影响的，包括车辆速度、地形起伏、路基条件、交通量等。

在实际设计中，需要对这些因素进行充分的评估，以确定合适的设计方案，以确保公路的安全性和舒适性。

3. 对竖曲线设计参数的认识在竖曲线设计中，凸度、坡度、曲线长度等参数都对公路的安全和舒适度有着直接的影响。

需要对这些参数有深入的理解和把握，合理设置参数值，才能确保设计的质量和合理性。

三、广度评估1. 综述竖曲线设计的发展历史竖曲线设计作为公路设计中的重要内容，其发展历史也颇为悠久。

从最早的简单的曲线设计，到如今的复杂公路设计软件的应用，竖曲线设计经历了多个阶段的发展和完善。

2. 分析竖曲线设计在公路工程中的应用竖曲线设计在公路工程中应用广泛，不仅能改善公路的舒适性和安全性，还能提高公路的通过能力和效率。

对竖曲线设计的研究和应用具有重要的现实意义。

3. 探讨竖曲线设计在不同地域和环境中的应变能力不同地域和环境的公路工程对于竖曲线设计的要求也有所不同，需要根据实际情况进行变通和调整。

对于不同地域和环境中的竖曲线设计要求的研究，有利于制定更加灵活和适用的公路设计方案。

四、总结与回顾在学习和实践中，我对公路勘测设计竖曲线设计有了更深入的了解和认识。

通过深度和广度的评估，我发现竖曲线设计影响因素多样，应用广泛，且具有一定的环境适应能力。

纵断面设计——竖曲线设计纵断面上相邻两条纵坡线相交的转折处，为了行车平顺用一段曲线来缓和，这条连接两纵坡线的曲线叫竖曲线。

竖曲线的形状，通常采用平曲线或二次抛物线两种。

在设计和计算上为方便一般采用二次抛物线形式。

纵断面上相邻两条纵坡线相交形成转坡点，其相交角用转坡角表示。

当竖曲线转坡点在曲线上方时为凸形竖曲线，反之为凹形竖曲线。

一、竖曲线如图所示，设相邻两纵坡坡度分别为i1 和i2，则相邻两坡度的代数差即转坡角为ω= i1-i2 ，其中i1、i2为本身之值，当上坡时取正值，下坡时取负值。

当i1- i2为正值时，则为凸形竖曲线。

当i1 - i2 为负值时，则为凹形竖曲线。

（一）竖曲线基本方程式我国采用的是二次抛物线形作为竖曲线的常用形式。

其基本方程为：若取抛物线参数为竖曲线的半径，则有：（二）竖曲线要素计算公式竖曲线计算图示1、切线上任意点与竖曲线间的竖距通过推导可得：2、竖曲线曲线长：L = Rω3、竖曲线切线长：T= TA =TB ≈ L/2 =4、竖曲线的外距：E =⑤竖曲线上任意点至相应切线的距离：式中：x —为竖曲任意点至竖曲线起点（终点）的距离, m；R—为竖曲线的半径，m。

二、竖曲线的最小半径(一)竖曲线最小半径的确定1.凸形竖曲线极限最小半径确定考虑因素（1）缓和冲击汽车行驶在竖曲线上时，产生径向离心力，使汽车在凸形竖曲线上重量减小，所以确定竖曲线半径时，对离心力要加以控制。

（2）经行时间不宜过短当竖曲线两端直线坡段的坡度差很小时，即使竖曲线半径较大，竖曲线长度也有可能较短，此时汽车在竖曲线段倏忽而过，冲击增大，乘客不适；从视觉上考虑也会感到线形突然转折。

因此，汽车在凸形竖曲线上行驶的时间不能太短，通常控制汽车在凸形竖曲线上行驶时间不得小于3秒钟。

（3）满足视距的要求汽车行驶在凸形竖曲线上，如果竖曲线半径太小，会阻挡司机的视线。

为了行车安全，对凸形竖曲线的最小半径和最小长度应加以限制。

竖曲线参数1. 竖曲线的定义与特点竖曲线是指在一维平面上，沿着垂直方向变化的曲线。

它是由一个或多个曲率半径不断变化的圆弧和直线段组成的。

竖曲线通常用于道路、铁路等交通工程中，用来平缓过渡两个不同坡度或高程的地点。

竖曲线有以下几个重要特点：•平滑性：竖曲线在不同坡度之间提供了平滑过渡，避免了急剧的高程变化对车辆或列车的冲击。

•安全性：通过合理设计竖曲线参数，可以确保车辆或列车在行驶过程中具有足够的视距和操控空间，提高行驶安全性。

•经济性：合理设计竖曲线参数可以使工程成本最小化，同时满足道路、铁路等交通工程的要求。

2. 竖曲线参数的确定方法在设计竖曲线时，需要确定以下几个重要参数：•切换坡度：切换坡度是指两个相邻坡度之间的高差差值。

切换坡度的确定需要考虑车辆或列车的运行速度、加速度等因素。

•曲率半径：曲率半径是指竖曲线上圆弧部分的半径。

曲率半径的选择需要根据设计标准和实际情况进行调整，以确保车辆或列车在竖曲线上能够平稳行驶。

•过渡长度：过渡长度是指竖曲线上圆弧和直线段之间的距离。

过渡长度的确定需要综合考虑车辆或列车的运行速度、加速度等因素，以及道路、铁路等交通工程的要求。

确定竖曲线参数的方法主要有以下几种：•经验法：根据实际经验和类似工程的设计数据，选择合适的竖曲线参数。

•图解法：通过绘制竖曲线图来确定参数，根据图中所示的坡度变化和高程变化来选择合适的参数。

•计算法：通过数学计算来确定参数，根据车辆或列车运行速度、加速度等因素，以及道路、铁路等交通工程要求进行计算。

3. 竖曲线参数设计原则在设计竖曲线时，需要遵循以下几个原则：•平稳性原则：竖曲线应该设计得平稳过渡，避免急剧的高程变化对车辆或列车的冲击。

•安全性原则：竖曲线应该保证车辆或列车在行驶过程中具有足够的视距和操控空间，提高行驶安全性。

•经济性原则：竖曲线应该在满足交通工程要求的前提下，尽量减少工程成本。

•美观性原则：竖曲线应该设计得美观大方，与周围环境相协调。

道路竖曲线设计
纵向坡度的改变是通过足够长的竖曲线来完成的，而且只要条件允许，竖曲线的设置地点要和平曲线协调，二者在长度上也要相近。

但在凸形竖曲线的预部和凹形竖曲线的底部不应设置小半径的平曲线，因为在这些地方设置半径过小的曲线会造成不良的视距条件。

在可能的情况下，竖曲线长度应不小于300米，其最小半径对凸曲线而言为1，8000米·，凹曲线最小半径为9，000米。

尽管有时受到具体地点的客观条件的限制，不得不采用长度小于300米，半径更小的竖曲线。

但在这情况下，仍应满足300米的视距要求。

竖曲线的最小长度(以米计)可按照下面的方法很方便地算出来。

首先把相邻两段切线以百分数表示的纵坡代效差求出来。

然后再乘以常数K，即为竖曲线的最小长度值。

凸曲线，K＝175，，凹曲线，K＝75。

例如，一条凸形竖曲线连接的两个路段，其一为升坡段，坡度值个3％，另一为降坡段，’坡度为—2％，纵坡的代数差则为+3％一(—2％)=5％，·K＝175，该曲线的最小长度应为5x175＝875(米)。

凹形竖曲线上的停车视距是考虑汽车前灯光柱能照到车行道上的物体。

例如一条凹形竖曲线的坡度从降坡—4％变到降级“—2％，坡度改变值为2％，该竖曲线最小长度应为2x75＝150(米)。

高速公路的主干道，竖曲线长度任何情况下都不得小于70米。