第2章 信号分析基础 题库-答案

3.2 教材第三章习题解答1. 计算以下诸序列的N 点DFT,在变换区间01n N ≤≤-内,序列定义为 （2）()()x n n δ=；（4）()(),0m x n R n m N =<<； （6）2()cos(),0x n nm m N Nπ=<<；（8）0()sin()()N x n w n R n =∙； （10）()()N x n nR n =。

解：（2）1,,1,0,1)()()(11-====∑∑-=-=N kn Wn k X N n N n kn Nδδ（4）1,,1,0,)sin()sin(11)()1(1-==--==---=∑N k m Nmk NeWWWk X m k Njk Nkm N N n kn Nπππ10,,0,11111212121)(2)(2)(2)(21)(21)(2-≤≤⎪⎩⎪⎨⎧-≠≠-===⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--+--=+=+-+----=+--=-∑∑N k m N k m k m N k m k N e e e e eek m Nj N k m Nj k m N j N k m N j N n nk m NjN n nk m Nj或且ππππππ（6）knNj mnNj N n mnNj N n knN eeeW mn N k X ππππ22121)(212cos )(---=-=+=∙⎪⎭⎫ ⎝⎛=∑∑（8）解法1 直接计算[])(21)()sin()(0008n Reejn R n w n x Nnjw njw N --==[]∑∑-=---=-==12180021)()(N n knNj njw njw N n knNeeejWn x k X π⎥⎥⎦⎤⎢⎢⎣⎡-----=⎥⎦⎤⎢⎣⎡-=+--=+--∑)2()2(12200000011112121k Nw j Njw k N w j N jw N n n Nw j n N w j e e ee je e jππππ）（）（ 解法2 由DFT 的共轭对称性求解因为[])()sin()cos()()(0070n R n w j n w n R en x N N njw +==[])(Im )()sin()(708n x n R n w n x N ==所以[][][])()(Im )(7078k X n x j DFTn jx DFT==即[])()(21)()(77708k N X k Xj k jX k X ---=-=*⎥⎥⎦⎤⎢⎢⎣⎡-----=⎥⎥⎦⎤⎢⎢⎣⎡-----=+-*---)11(1121)11(1121)2()2()(2()2(00000000k Nw j Njw k N w j N jw k N Nw j N jw k N w j N jw e e e e j e e e e j ππππ结果与解法1所得结果相同。

信号与信息处理基础习题及题解目录第1章绪论 (3)第2章连续时间信号的时域分析 (3)第3章连续时间信号的频域分析 (8)第4章连续时间信号的复频域分析 (15)第5章离散时间信号的时域分析 (19)第6章离散傅里叶变换 (22)第7章离散时间信号的复频域分析 (27)第一章1.1 结合具体实例，分析信息、消息和信号的联系与区别。

答：具体实例略。

信息、消息和信号三者既有区别又有联系，具体体现在：⑴ 信息的基本特点在于其不确定性，而通信的主要任务就是消除不确定性。

受信者在接收到信息之前，不知道发送的内容是什么，是未知的、不确定性事件。

受信者接收到信息后，可以减少或者消除不确定性。

⑵ 消息是信息的载体。

可以由消息得到信息，以映射的方式将消息与信息联系起来，如果不能建立映射关系就不能从消息中得到信息。

例如，一个不懂得中文的人看到一篇中文文章，就不能从中获取信息。

⑶ 信号是消息的具体物理体现，将消息转换为信号才能够在信道（传输信号的物理媒质，如空气、双绞线、同轴电缆、光缆等）中传输。

1.2 说明连续时间信号与模拟信号、离散时间信号与数字信号间的联系和区别。

答：按照时间函数取值的连续性与离散性可将信号划分为连续时间信号与离散时间信号，简称连续信号与离散信号。

第二章2.2 试写出题2.2图示各波形的表达式。

题2.2图解：左图：()()()[]()()()[]31312-------=t u t u t t u t u t f()()()()()33112--+---=t u t t u t t u中图：()()()()()321-----+=t u t u t u t u t f 右图：()()()()221---+=t u t u t u t f连续时间信号离散时间信号幅值连续幅值离散模拟信号幅值连续幅值离散数字信号抽样2.3 试画出时间t 在（-4，6）内以下信号的波形图。

⑴ t 2πsin ；⑵()1 2-t πsin ；⑶()t t u 21πsin -；⑷ ()t t u 2πsin ； ⑸()()1 2-t t u πsin ； ⑹()()1 21--t t u πsin 。

第二章2.1 判断下列序列是否是周期序列。

若是,请确定它的最小周期.（1）x （n ）=Acos(685ππ+n ） （2)x （n)=)8(π-ne j（3）x （n)=Asin(343ππ+n ) 解 （1）对照正弦型序列的一般公式x （n ）=Acos （ϕω+n )，得出=ω85π。

因此5162=ωπ是有理数，所以是周期序列。

最小周期等于N=)5(16516取k k =。

（2）对照复指数序列的一般公式x （n ）=exp[ωσj +］n,得出81=ω。

因此πωπ162=是无理数,所以不是周期序列。

(3）对照正弦型序列的一般公式x （n)=Acos(ϕω+n ），又x （n)=Asin （343ππ+n ）＝Acos （-2π343ππ-n )＝Acos(6143-n π）,得出=ω43π.因此382=ωπ是有理数，所以是周期序列。

最小周期等于N=)3(838取k k =2.2在图2.2中，x （n ）和h(n)分别是线性非移变系统的输入和单位取样响应。

计算并列的x （n ）和h （n)的线性卷积以得到系统的输出y(n ）,并画出y(n)的图形。

(a)1111(b)(c)111110 0-1-1-1-1-1-1-1-1222222 33333444………nnn nnnx(n)x(n)x(n)h(n)h(n)h(n)21u(n)u(n)u(n)a n ===22解 利用线性卷积公式y(n ）=∑∞-∞=-k k n h k x )()(按照折叠、移位、相乘、相加、的作图方法,计算y(n)的每一个取样值。

（a ） y （0）=x （O)h （0）=1y （l ）=x （O ）h(1)+x （1)h （O)=3y （n)=x(O)h （n ）+x （1)h(n-1)+x(2)h （n —2)=4,n ≥2 （b) x(n ）=2δ(n ）-δ（n-1）h(n)=-δ（n)+2δ（n —1)+ δ(n —2）y(n ）=-2δ(n)+5δ（n —1）= δ(n-3） (c ） y （n ）=∑∞-∞=--k kn k n u k u a)()(=∑∞-∞=-k kn a=aa n --+111u （n ）2。

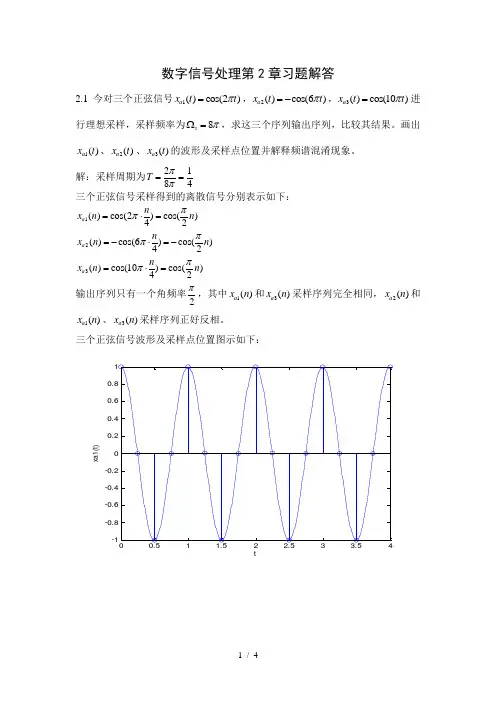
数字信号处理第2章习题解答2.1 今对三个正弦信号1()cos(2)a x t t π=，2()cos(6)a x t t π=-，3()cos(10)a x t t π=进行理想采样，采样频率为8s πΩ=，求这三个序列输出序列，比较其结果。

画出1()a x t 、2()a x t 、3()a x t 的波形及采样点位置并解释频谱混淆现象。

解：采样周期为2184T ππ== 三个正弦信号采样得到的离散信号分别表示如下：1()cos(2)cos()42a n x n n ππ=⋅=2()cos(6)cos()42a n x n n ππ=-⋅=-3()cos(10)cos()42a n x n n ππ=⋅=输出序列只有一个角频率2π，其中1()a x n 和3()a x n 采样序列完全相同，2()a x n 和1()a x n 、3()a x n 采样序列正好反相。

三个正弦信号波形及采样点位置图示如下：tx a 1(t )tx a 2(t )tx a 3(t )三个正弦信号的频率分别为1Hz 、3Hz 和5Hz ，而采样频率为4Hz ，采样频率大于第一个正弦信号频率的两倍，但是小于后两个正弦信号频率的两倍，因而由第一个信号的采样能够正确恢复模拟信号，而后两个信号的采样不能准确原始的模拟信号，产生频谱混叠现象。

2.3 给定一连续带限信号()a x t 其频谱当f B >时，()a X f 。

求以下信号的最低采样频率。

（1）2()a x t （2）(2)a x t （3）()cos(7)a x t Bt π 解：设()a x t 的傅里叶变换为()a X j Ω（1）2()a x t 的傅里叶变换为22()[()]Ba a BX j X j d ππωωω-⋅Ω-⎰因为22,22B B B B πωππωπ-≤≤-≤Ω-≤ 所以44B B ππ-≤Ω≤即2()a x t 带限于2B ，最低采样频率为4B 。

P57 1.4 Determine the following sequences whether they are periodic or not. If they are periodic, determine their periodicity.(1) 3()cos()78x n A n ππ=-, A 是常数。

解：(a.)用定义求解: 3()()cos(())78x n x n N A n N ππ=+=+-33cos()778A n N πππ=+-只要327N k ππ=，且N 和k 都是整数，则x(n)是周期序列214337N k ππ==，有当k=3时，周期为最小整数N=14。

(b.)用公式：已知37ωπ=可得2214337N k ππωπ===该序列是周期序列且其周期为最小整数N=14 （2）1()8()j n x n eπ-=解：(a.)用定义求解: 1(())8()()j n N x n x n N e π+-=+=11()88j n N e π+-=只要128N k π=，且N 和k 都是整数，则x(n)是周期序列因为K 取任意的整数，N 仍然是无理数，故该序列不是周期序列(b.)用公式：已知18ω=可得221618N k πππω===16N k π=K 取任意的整数，N 仍然是无理数，故该序列不是周期序列1.6 The unit pulse response h(n) of system are given below, try to determine their causality and stability.(1)δ(n)因果稳定解：0,()()0n h n n δ<==，所以系统是因果()()(0)1n n h n n n δδ∞∞=-∞=-∞====∑∑，所以系统稳定(2) δ(n-0n )，0n >=0或0n <0解：0()1n n δ==0n >=0时，0n <有0()()0h n n n δ=-=，所以系统是因果 0n <0时，0n <有0()()0h n n n δ=-≠，所以系统是非因果00()()()1n n h n n n n n δδ∞∞=-∞=-∞=-===∑∑，所以系统稳定0n >=0，因果稳定；0n <0，非因果稳定(3)u(3-n)，非因果非稳定解：当0n <时，()(3)0h n u n =-≠，所以系统是非因果的3()(3)11...n n h n u n ∞=-∞=-∞=-=++⇒∞∑∑，所以系统不稳定(4) 3()nu n 因果非稳定解：当0n <时，()3()0nh n u n ==，所以系统是因果的。

第2章 习 题2-1 求下列齐次微分方程在给定起始状态条件下的零输入响应（1）0)(2)(3)(22=++t y t y dt d t y dt d ；给定：2)0(,3)0(==--y dt dy ； （2）0)(4)(22=+t y t y dt d ；给定：1)0(,1)0(==--y dtd y ；（3）0)(2)(2)(22=++t y t y dt d t y dt d ；给定：2)0(,1)0(==--y dt dy ； （4）0)()(2)(22=++t y t y dt d t y dt d ；给定：2)0(,1)0(==--y dtdy ； （5）0)()(2)(2233=++t y dt d t y dt d t y dt d ；给定：2)0(,1)0(,1)0(22===---y dt d y dt d y 。

（6）0)(4)(22=+t y dt d t y dt d ；给定：2)0(,1)0(==--y dtdy 。

解：（1）微分方程的特征方程为：2320λλ++=，解得特征根：121, 2.λλ=-=- 因此该方程的齐次解为：2()t th y t Ae Be --=+.由(0)3,(0)2dy y dt--==得:3,2 2.A B A B +=--=解得:8, 5.A B ==- 所以此齐次方程的零输入响应为:2()85tty t e e--=-.（2）微分方程的特征方程为：240λ+=，解得特征根：1,22i λ=±.因此该方程的齐次解为：()cos(2)sin(2)h y t A t B t =+.由(0)1,(0)1d y y dx --==得:1A =,21B =,解得:11,2A B ==. 所以此齐次方程的零输入响应为:1()cos(2)sin(2)2y t t t =+.（3）微分方程的特征方程为：2220λλ++=，解得特征根:1,21i λ=-± 因此该方程的齐次解为：()(cos()sin())th y t e A t B t -=+.由(0)1,(0)2dy y dx--==得:1,2,A B A =-= 解得:1,3A B ==.所以齐次方程的零输入响应为:()(cos()3sin())ty t e t t -=+.（4）微分方程的特征方程为：2210λλ++=，解得二重根:1,21λ=-.因此该方程的齐次解为：()()th y t At B e -=+. 由(0)1,(0)2dy y dx--==得:1,2,B A B =-=解得:3, 1.A B == 所以该方程的零输入响应为:()(31)ty t t e -=+.（5）微分方程的特征方程为：3220λλλ++=，解得特征根: 1,21λ=-,30λ=. 因此该方程的齐次解为：()()th y t A Bt C e -=++.由22(0)1,(0)1,(0)2d d y y y dx dt---===得:1,1,22A C B C C B +=-=-=. 解得:5,3,4A B C ==-=-.所以方程的零输入响应为:()5(34)ty t t e -=-+.（6）微分方程的特征方程为：240λλ+=，解得特征根:120,4λλ==-. 因此该方程的齐次解为：4()th y t A Be -=+.由(0)1,(0)2d y y dx --==得:1,42A B B +=-=.解得:31,22A B ==-. 所以此齐次方程的零输入响应为:431()22ty t e -=-.2-2 已知系统的微分方程和激励信号，求系统的零状态响应。

第二章 基本放大电路自测题一、（1）× （2）√ （3）× （4）× （5）√ （6）× （7）× 二、（a ）不能。

因为输入信号被V BB 短路。

（b ）可能（c ）不能。

因为输入信号作用于基极与地之间，不能驮载在静态电压之上，必然失真。

（d ）不能。

晶体管将因发射结电压过大而损坏。

（e ）不能。

因为输入信号被C 2短路。

（f ）不能。

因为输出信号被V CC 短路，恒为零。

（g ）可能。

（h ）不合理。

因为G-S 间电压将大于零。

（i ）不能。

因为T 截止。

三、（1）3 )( 565 )(BQ CEQ CC BQ BEQ CC I U V I U V β--；（2）0.3120- 'o LC L i o U R R R U U ⋅-＋；四、（1）A （2）C （3）B （4）B 五、（1）C ，D E （2）B （3）A C D （4）A B D E （5）C （6）B C E ，A D 六、习题2.1 e b c 大 大 中 大 c b c 小 大 大 小 b e c 大 小 小 大2.2（a ）将－V CC 改为＋V CC 。

（b ）在＋V CC 与基极之间加R b 。

（c ）将V BB 反接，且加输入耦合电容。

（d ）在V BB 支路加R b ，在－V CC 与集电极之间加R c 。

2.3 图P2.3所示各电路的交流通路；将电容开路即为直流通路，图略。

2.4空载时：I BQ ＝20μA ，I CQ ＝2mA ，U CEQ ＝6V ；最大不失真输出电压峰值约为5.3V 。

带载时：I BQ ＝20μA ，I CQ ＝2mA ，U CEQ ＝3V ；最大不失真输出电压峰值约为2.3V 。

2.5（1）× （2）× （3）× （4）√ （5）× （6）× （7）× （8）√（9）√ （10）× （11）× （12）√2.6 （1）6.4V （2）12V （3）0.5V （4）12V （5）12V 2.7Ω==-≈⋅+≈Ω≈≈=-≈-=Ω≈++=≈-=≈=≈--=k 5 93 k 3.1 308k 3.1mV26)1( V 2.6mA76.1 Aμ22o 'c ubes beusbe be b i becuEQbb be c CQ CC CEQ BQ CQ BEQ bBEQCC BQ R R A r R r A r r R R r R A I r r R I V U I I RU R U V I Q ∥，空载时：：βββ47 115 V3.2)(k 3bes bebe 'L L c CQ Lc LCEQ L -≈⋅+≈-≈-=≈-+=Ω=uusuA r R r A r R A R R I R R R U R β∥时：2.8（a ）饱和失真，增大R b ，减小R c 。

第二章习题2-1 已知系统的微分方程为te t y dtt dy dt t y d 322)(2)(3)(-=++ 且初始条件为1)0(='y 和2)0(=y 。

求系统的自由分量和强制分量。

解：系统的自由分量为微分方程的齐次解，即0)(2)(3)(22=++t y dtt dy dt t y d 特征方程0232=++αα求得特征根：2,121-=-=αα，则系统的通解为ttn e c e c t y 221)(--+=，21,c c 为待定系数。

微分方程的右边是指数形式的激励，故设特解为tf Ae t y 3)(-=，A 为待定系数。

将特解代入微分方程， t f Ae t y 33)(--='，t f Ae t y 39)(-=''t t t t e Ae Ae Ae 3333299----=+-求得21=A ，则t f e t y 321)(-=，于是系统全解：t t t e e c e c t y 322121)(---++=既有 t t t e e c e c t y 3221232)(------='，根据给定的初始条件有：22121=++c c123221=---c c求得421121-==c c ,所以系统的自由响应和强制响应分别为：t t n e e t y 24211---=)(t f e t y 321)(-=2-2 求下列信号对的卷积)()()(n h n x n y *=(2))(2)(n u n x n-=，)()(n u n h = (5))(n x 和)(n h 如题图2-2所示。

(2)解：∑∞-∞=--=k k k n u k u n y )()()(2 当0<n 时， 1221122+-∞==-==∑n n nk kn y )(当0≥n 时， 2211120=-==∑-∞=k k n y )((5)根据题图2-2所示图形可得： )3(3)2(2)1()]4()1([)(-+-+-=---=n n n n u n u n n x δδδ)2(2)1()]3()1([)(-+-=---=n n n u n u n n h δδ∑∞-∞=-=k k n h k x n y )()()(第一步画出)(k x 和)(k h 的草图； 第二步画出)(k h -的草图； 第三步画出)(k n h -的草图； 第四步考察n 从-∞至∞变化时，)(k x 与)(k n h -的非零值交点区间。