当前位置：文档之家 › 第二章信号分析基础

第二章信号分析基础

  • 格式：ppt
  • 大小：923.00 KB
  • 文档页数：64

下载文档原格式

  / 64

合集下载

第2章 信号分析基础 题库-答案

第2章 信号分析基础 题库-答案

（1）傅里叶级数实数形式的幅值谱、相位谱；
（2）傅里叶级数复数形式的幅值谱、相位谱；
（3）幅值谱密度。
解：（1）实数形式
傅里叶级数三角形式的展开式：
x(t)
a0 2
n1
(an
cos n0t
bn
sin
n0t )
x(t)
2 2
Acos(0t)
2 2
A sin(0t )
得： a0
0 ， an
形脉冲。
x(t)
t
x1 (t )
x2 (t )
图2-31
解：矩形脉冲信号
x(t
)
E 0
| t | T1 的频谱密度 | t | T1 t
t
X ()
T1 T1
Ee
jt dt
2ET1
sinc(T1)
所以
X1
(
)
sinc(
1 2
)
，
X
2
(
)
3
sinc(
3 2
)
x(t)
1 2
x1 (t
2.5)
x2 (t
过程： T 0
A2
T 1 cos 2t dt
T0
2
A2 2
18.求正弦信号 xt Asin( t ) 的概率密度函数 p(x)。
解：
公式： p(x) lim P(x x(t) x x)
x0
x
过程：
在一个周期内Tx0 t1 t2 P[x x(t) x x] lim Tx Tx0
答：充分条件：绝对可积
充要条件：
（D） a X a f
6．判断对错：1、 随机信号的频域描述为功率谱。（ V ）

(3)第2章 信号分析基础

(3)第2章 信号分析基础

2.3 非周期信号与连续频谱
•
图2-5 非周期信号
2.3 非周期信号与连续频谱
• 2.3.1傅立叶变换
• 当周期T趋于无穷大时，相邻谱线的间隔 趋 近于无穷小，从而信号的频谱密集成为连续频谱 。同时，各频率分量的幅度也都趋近于无穷小， 不过，这些无穷小量之间仍保持一定的比例关系 。为了描述非周期信号的频谱特性，引入频谱密 度的概念。令
• 对于周期信号，在时域中求得的信号功率与在频域中求得 的信号功率相等。
2.3 非周期信号与连续频谱
• 2.3 非周期信号与连续频谱 • 非周期信号包括准周期信号和瞬态信号两种，其频谱
各有独自的特点：周期信号的频谱具有离散性，各谐波分 量的频率具有一个公约数——基频。但几个简谐具有离散 频谱的信号不一定是周期信号。只有各简谐成分的频率比 是有理数，它们才能在某个时间间隔后周而复始，合成的 信号才是周期信号。若各简谐信号的频率比不是有理数， 合成信号就不是周期信号，而是准周期信号。因此准周期 信号具有离散频谱，例如多个独立激振源激励起某对象的 振动往往是这类信号对于瞬态信号，不能直接用傅立叶级 数展开，而必须应用傅立叶变换的数学方法进行分解。
第2章 信号分析基础
2.1 信号的分类与描述
• 2.1 信号的分类与描述
• 2.1.1 信号的分类
• 信号是反映被测对象状态或特性的某种物理量。以信 号所具有的时间函数特性分类，信号主要分为确定性信号 与随机信号、连续信号与离散信号等。
• 1. 确定性信号与随机信号
• 确定性信号是指可以用精确的数学关系式来表达的信 号。确定性信号根据它的波形是否有规律地重复又可进一 步分为周期信号和非周期信号两种。
•
（2-21） F( j) lim Fn T 1 / T

第二章信号分析基础(频谱)

第二章信号分析基础(频谱)

（1）
A0 a0
An
an bn
2
2
bn n arctg an
周期信号的频谱分析
西安工业大学机电学院
复指数形式： 将三角函数形式中的正余弦用欧拉公式代换
e j e j cos 2
则：

e j e j sin 2j
带入并合并同类项
a0 an jbn jn0t an jbn jn0t f (t ) [ e e ] 2 n 1 2 2 a0 an jbn jn0t an jbn jn0t e e 2 n 1 2 2 n 1 an jbn jn0t e Cn e jn0t 2 n n
则：c1x1(t)+c2x2(t) ←→ c1X1(f)+c2X2(f)
例子：求下图波形的频谱
用线性叠加定理简化 X1(f)
+
X2(f)
2.4 傅立叶变换的性质 c.对称性
西安工业大学机电学院
若 x(t) ←→ X(f)，则 X(t) ←→ x(-f)
证明： 以－t替换t: 以f换t: 所以：
x(t )
∴当T0→∞时，Δω→0 上式变为：
T / 2
0
T0 / 2
f (t )e jn0t dt ]e jn0t
f (t )
＋

1 ＋ [ f (t )e jt dt ]e jt d 2
1 ＋ jt F e d 2
西安工业大学机电学院


X ( f )e j 2ft df X ( f )e j 2ft df
x(t )


x( f ) X (t )e j 2ft dt

工程测试技术 第2章 信号分析基础-3

工程测试技术 第2章 信号分析基础-3

第二章、信号分析基础
Page 2 华中科技大学机械学院
2.5 信号的频域分析
信号频域分析是采用傅立叶变换将时域信号x(t)变换为 频域信号X(f)，从而帮助人们从另一个角度来了解信号的特 征。
傅里叶 变换
8563A
SPECTRUM ANALYZER 9 kHz - 26.5 GHz
第二章、信号分析基础
2.5 信号的频域分析
频域分析
Page 25 华中科技大学机械学院
吉布斯现象(Gibbs)
• 吉布斯现象是由于展开式在间断点邻域不能均匀收敛 引起的。
• 例：方波信号
x(t)
T
T
t
2.5 信号的频域分析
频域分析
Page 26 华中科技大学机械学院
N=1
2.5 信号的频域分析
Page 27 华中科技大学机械学院
用线性叠加定理简化
X1(f)
+Page 38 华中科技大学机械学院
5、频谱分析的应用
频谱分析主要用于识别信号中的周期分量，是信号分析 中最常用的一种手段。
在齿轮箱故障诊断中，可
以通过齿轮箱振动信号频谱分 析，确定最大频率分量，然后 根据机床转速和传动链，找出 故障齿轮。
2 T
T /2
T /2 x(t) sin n0tdt;
ω0―基波圆频率； f0 ―基频：f0= ω0/2π
An an2 bn2 ;
n
arctan bn an
;
2.5 信号的频域分析
傅里叶级数的复数表达形式：
x(t) Cne jn0t , (n 0,1,2,...) n
Page 9 华中科技大学机械学院
2.5 信号的频域分析

【复习笔记】信号分析基础

【复习笔记】信号分析基础

第二章 信号分析基础1、信号分析中常用函数包括：δ函数、sinc(t)函数、复指数函数e st① δ函数具有“抽样（乘积）、筛选（积分）、卷积”特性，其拉氏变换和傅氏变换的值均为1。

② 卷积特性的表达式为)()()()()(t f d t f t t f =-=*⎰+∞∞-ττδτδ，τ为两信号之间的时差。

③ sinc(t)函数又称为闸门函数、滤波函数或内插函数，分别对应其用处：闸门（或抽样）、低通滤波、采样信号复原时sinc(t)函数叠加构成非采样点波形。

④ 复指数函数e st 中出现的“负频率”是与负指数相关联的，是数学运算的结果，并无确切的物理含义。

2、一个信号不能够在时域或频域都是有限的。

3、信号的时域统计分析：均值x μ、均方值ψ2x 、方差σ2x 。

三者具有如下关系：2x2x 2x μσψ+= 式中，ψ2x （又称平均功率，平均能量的一种表达）表达了信号的强度； σ2x 描述了信号的波动量； μ2x 描述了信号的静态量。

4、各态历经过程：此过程中的任一个样本函数x(t)都经历了过程的各种状态，从它的一个样本函数x(t)中可以提取到整个过程统计特征的信息。

5、相关函数的性质：① 自相关函数R x (τ)是τ的偶函数，满足：)()(ττ-=x x R R 。

② 互相关函数R xy (τ)是τ的非奇非偶函数，满足：)()(ττ-=yx xy R R 。

③ 当τ=0时，自相关函数具有最大值。

对于功率信号，若均值μx =0，则在τ=0点处，有ψ2x =σ2x =R x (τ)。

④ 周期信号的R x (τ)仍然是与原信号同频率的周期信号，但不具有原信号的相位信息。

⑤ 两周期信号（同频）的R xy (τ)仍然是与原信号同频率的周期信号，但保留了原信号的相位信息。

⑥ 两个不同频的周期信号互不相关，其互相关函数R xy (τ)=0。

⑦ 随机信号的R x (τ)将随|τ|值增大而很快趋于0。

有限带宽白噪声信号的R x (τ)是一个sinc(τ)型函数，即可说明。

工程测试技术基础 第二部分 信号分析基础

工程测试技术基础 第二部分 信号分析基础
a)能量信号 在所分析的区间（-∞，∞），能量为有限值的信号称
为能量信号，满足条件：
x2 (t)dt
一般持续时间有限的瞬态信号是能量信号。
瞬态信号
2.1 信号的分类与描述
b)功率信号 在所分析的区间（-∞，∞），能量不是有限值．此时，
研究信号的平均功率更为合适。
T
lim

数学期望，称为相关性，表征了x、y之间其的中一关个联可程以度测。量的量
cxy xy x y
E[(xx )( y的 的y )变变] 化化来。表示另一个量
E[(xx )2 ]E[( y y )2 ]1/ 2
y
y
y
y
x
x
xy 1
xy 1
x
0 xy 1
b) sinc 函数
sin c(t) sin t , or, sint , ( t )
t
t
性质：
波形
偶函数；
闸门(或抽样)函数；
滤波函数；
内插函数。
2.1 信号的分类与描述
c) 复指数函数
est et e jt
t
et cost et sint ; s j
瞬态信号
瞬态信号:持续时间有限的信号，如 x(t)= e-Bt . Asin(2*pi*f*t)
2.1 信号的分类与描述
c)非确定性信号：不能用数学式描述，其幅值、相位变化 不可预知，所描述物理现象是一种随机过程。
噪声信号(平稳)
噪声信号(非平稳)
统计特性变异
2.1 信号的分类与描述 2 能量信号与功率信号
（3）卷积特性

f (t) * (t) f ( ) (t )d f (t)

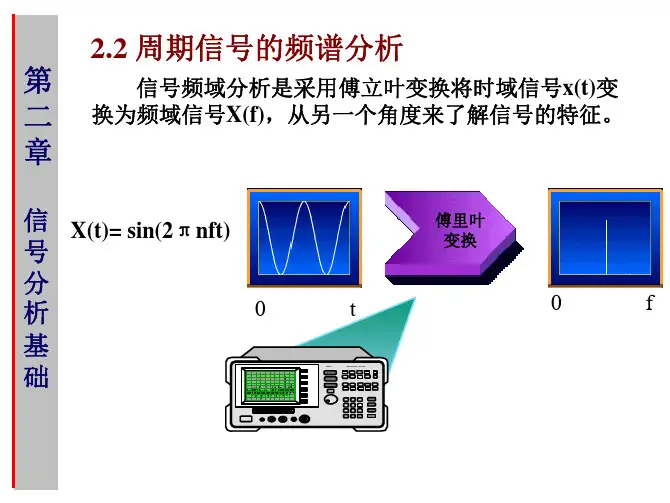
2 信号分析基础(频谱分析)

2 信号分析基础(频谱分析)

(2.69)
傅 里 叶 变 换 与 非 周 期 信 号 的 分 解
式2.68称为 x t 的傅立叶变换，称式2.69为 X 的 傅立叶逆变换，两者称为傅立叶变换对，可记为
x t X
IFT
FT
2 f 代入傅立叶积分式中，则式2.68, 2.69变为
X f x t e j 2 ft dt
Im[X ( f )] ( f ) arctgRe[ X ( f )]
x (t ) 1 X ( )e jt d 2 X ( ) x (t )e jt dt
X f 连续幅值谱
f

连续相位谱
X 频谱密度函数
2.2 周期信号的频谱分析 第 二 章
信号频域分析是采用傅立叶变换将时域信号x(t)变 换为频域信号X(f)，从另一个角度来了解信号的特征。
信 X(t)= sin(2πnft) 号 分 0 析 基 础
傅里叶 变换
t
8563A
SPECTRUM ANALYZER 9 kHz - 26.5 GHz
0
f
频域分析的概念 周 期 信 号 的 频 谱 分 析
傅 里 叶 变 换 与 非 周 期 信 号 的 分 解
T0 T0 , 设有一个周期信号x(t)在区间 2 2
以傅立叶级数表示为
x t
n
ce
n

jn0t
1 式中 cn T0

T0 2 T 0 2
x t e
jn0t
dt
将其代入上式则得
n n
幅频谱 相频谱
频谱图的概念 周 期 信 号 的 频 谱 分 析

工程测试与信号处理第二章信号分析基础1

工程测试与信号处理第二章信号分析基础1

(a) 拉氏变换:
(s) (t)est dt 1
(b) 傅氏变换:
( f ) (t )e j2ft dt 1
第二章 信号分析的基础
中原工学院 机电学院
2.sinc函数
sinc(t)函数又称为抽样函数、滤波函数或内插函数，在许多场合
下频繁出现.其定义为
sin c(t) sin t , or, sin t , ( t )
离散时间信号:在若干时间点上有定义
采样信号
第二章 信号分析的基础
中原工学院 机电学院
离散时间信号可以从试验中直接得到，也可能从连续时间信 号中经采样而得到。
典型离散时间信号有单位采样序列、阶跃序列、指数序列等.
单位采样序列用δ(n)表示，定义为:
(n)
0, n 0 1, n 0
此序列在n=0处取单位值1，其余点上都为零(图2-3 (a ) ).单位采样序
物理信号具有如下性质: (1)必然是能量信号.即时域内有限或满足可积收敛条件; (2)叠加、乘积、卷积运算以后仍为物理信号.
第二章 信号分析的基础
中原工学院 机电学院
六、信号分析中常用的函数
1. 脉冲函数—函数
函数表示一瞬间的脉冲. 狄拉克(Dirac)于1930年在量子力学中
引入了脉冲函数.从数学意义上讲，脉冲函数完全不同于普通函数，
第二章 信号分析的基础
二、能量信号与功率信号 1.能量信号
中原工学院 机电学院
在所分析的区间（-∞，∞），能量为有限值的信号称为 能量信号，满足条件：
x 2 (t )dt
一般持续时间有限的瞬态信号是能量信号。
第二章 信号分析的基础
中原工学院 机电学院
2. 功率信号

信号分析基础

信号分析基础

确定性信号又可分为周期信号和非周期信号 随机信号又可分平稳和非平稳的信号两种
周期信号是经过一定时间可以重复出现的信号， 满足条件：
x(t)=x(t+Nt) 式中：T——周期，T＝2π／ω0；
ω0——基频 N＝0，十1…
确定信号与随机信号
• 当信号是一确定的时间函数时，给定某一时 间值，就可以确定一相应的函数值。这样的 信号称为确定信号。
x(t)x(t) x(t )x(t ) 2x(t)x(t )
两边取时间T的平均值并取极限
lim 1
T
x(t)x(t)dt lim
1
T
x(t )x(t )dt
lim
1
T
2x(t)x(x )dt
T T 0
T T 0
T T 0
R(0) R( )
这个性质极为重要，它是相关技术 确定同名点的依据
3、数字相关
数字相关是利用计算机对数字影像进 行数值计算的方式完成影像的相关 二维相关
搜 索 区
目标区
测相 度似
性
c,r
maxij
i j
i0 j0
l
2 k
2
n 2
, , i0
l 2
n 2
m 2
, , i0
k 2
m 2
4．工程应用
2.4 信号的频域分析
确定信号的时间特性
• 表示信号的时间函数，包含了信号的全部 信息量，信号的特性首先表现为它的时间 特性。
R( ) lim 1
T
x(t)x(t )dt
T 2T T
lim 1
T
x(t )x(t)dt
T 2T T
lim
T

第二章 信号分析基础(随机信号和相关分析)090310

第二章 信号分析基础(随机信号和相关分析)090310

电感式轮廓 仪测量表面
性质4:提取出回转误差等周期性的故障源。
西安工业大学机电学院
案例：自相关测转速
理想信号
实测信号
自相关系数
干扰信号
从自相关图可以确定周期因素的 频率，从而得到转速大小。
性质4：可提取周期性转速成分。
西安工业大学机电学院
案例：互相关分析对地下输油管道漏损位置的探测
x1,x2处放置传感器1，2，漏损处k视为向两侧传播声波的声源。因两 传感器位置离漏损处不等，其声波传到传感器就有时差，信号x1,x2 做相关分析，找出相关值最大时的τ ，即可确定漏损位置。 （在互相关图上， τ= τm处，Rx1x2(τ)的最大值τm就是时差）
非线性；
西安工业大学机电学院
西安工业大学机电学院
西安工业大学机电学院
2.6 随机信号 二. 幅值域描述 1．均值：
西安工业大学机电学院
u x lim
2．方差：
1 T
1 T
T
0
0
T
T
x (t ) d t
――直流分量
x
2
lim
T
[ x ( t ) u x ] 2 d t ――波动程度/分量
其正平方根即为标准偏差，是随机数据分析的重要参数。
X1
S 1 2 v (t 2 t 1) 1 2 v m 处的距离 度
s 两传感器的中心至漏损
X2
v 声音在管道中的传播速
西安工业大学机电学院
案例：地震位置测量
设想3座地震观测台记录同一个地震，且位于震源的不同方向上。这3座台站 的观测人员能够读到P波抵达时间，有时也读到S波的抵达时间（因为P波传播 速度比S波传播速度大约快2倍，所以这两种波传播得越远，它们的波前分离 间隔就越宽）。如果有了P波和S波抵达的时间，从这两种波型抵达某台时间 间隔将可以直接求得震源到该记录台的距离。然后，画3个圆，每个圆以一座 地震台为圆心，半径是计算得到的距离（震中距）。这3个圆将相交，至少是 近似的相交于所要求的震中。

第二章-信号分析与信息论基础

第二章-信号分析与信息论基础
设ξ(t)表示一个随机过程，则在任意一个时刻t1 上，ξ(t1)是一个随机变量。显然，这个随机变量的统 计特性，可以用概率分布函数或概率密度函数去描述。
4、随机过程的数字特征 随机过程的数字特性，比如，随机过程的数学期望、
方差及相关函数等。 1）数学期望
随机过程ξ(t)的数学期望被定义为
可把t1直接写成t。随机过程的 数学期望被认为是时间t的函数。
2.1 确知信号分析
信号是通过电的某一物理量（如电压或电流）表 示出的与时间t之间的函数关系。 确知信号：能用函数表达式准确表示出来的信号。它 与时间的关系是确知的。 随机信号：与上述相反。
通信中传输的信号及噪声都是随机信号。
2.1.1 周期信号与非周期信号 周期信号：满足条件 s(t)=s(t+T0) -∞＜t＜∞，T0＞0 非周期信号：不满足上述条件。 功率信号：信号在（0，T）内的平均功率S(式2-2)值为 一定值。 能量信号：当T→ ∞时，式(2-3)是绝对可积的。
解： Γ[COS ω0 t]= π[δ(ω- ω0)+ δ(ω+ω0)] 冲激 强度为π，根据卷积定理：
Γ[f(t)COS ω0 t] =（1/2 π)F(ω)* {π[δ(ω- ω0)+ δ(ω+ω0)] }
=(1/2) [F(ω- ω0)+ F(ω+ω0)]
2.1.3 信号通过线性系统
线性系统：输出信号与输入信号满足线性关系（允许
说，如果对于任意的n和τ，随机过程ξ(t)的n维概率
密度函数满足：
则称ξ(t)是平稳随机过程。
6、广义平稳过程 广义平稳概念：若一个随机过程的数学期望及方差 与时间无关，而其相关函数仅与τ有关，则称这个随

第2章 信号分析基础 题库-答案

第2章 信号分析基础 题库-答案

第二章 信号分析基础练习题：2.1 信号的分类及其基本参数1.测试的基本任务是获取有用的信息，而信息总是蕴涵在某些物理量之中，并依靠它们来传输的。

这些物理量就是 信号 ，其中目前应用最广泛的是电信号。

*2.确定信号包括 周期信号 、 准周期信号 和 瞬态信号 。

3.信号的时域描述，以 时间 为独立变量；而信号的频域描述，以 频率 为独立变量。

4. 描述随机信号的时域特征参数有 均值 、 均方值 、 方差 。

5.周期信号的频谱具有三个特点： 离散型 、 谐波形 、 收敛性 。

6.非周期信号包括 准周期 信号和 瞬态 信号。

7.信号x(t)的均值μx 表示信号的 直流 分量，方差2x σ描述信号的 波动程度 。

8.cos2( 1.5)t t dt πδ∞-∞-⎰= -1 。

9. 某随机信号的方差为2x δ，均方值为2x ψ，均值为x μ，则三者之间存在关系式:222x x x ψμσ=+ 。

10.信号的概率密度函数表示 信号幅值落在指定区间的概率 。

11.信号的数学表达式一般包含信号的 周期 、 频率 、 幅度 、 相位 。

12.下列信号中功率信号是（ ）。

A.指数衰减信号B.正弦信号、C.三角脉冲信号D.矩形脉冲信号 13.周期信号x(t) = sin(t/3)的周期为（ ）。

A. 2π/3B. 6πC. π/3D. 2π 14.不能用确定的数学公式表达的信号是（ ）A.复杂周期信号B.瞬态信号C.随机信号D.非周期信号 15.下列信号中周期函数信号是（ ）。

A.指数衰减信号B.随机信号C.余弦信号、D.三角脉冲信号 16.)(t ∂为单位脉冲函数，则)(at ∂的冲激强度为（ ） A |a| B a C 1/a D|1/a|17.求正弦信号()t A t x ωsin =的均方值2x ψ。

解：公式：22201[()]lim()T x E x t x t dt Tψ==⎰ 过程：2202202021(sin )sin 1cos 222T x TTA t dt TA tdt TA tdt T A ψωωω==-==⎰⎰⎰18.求正弦信号())sin(ϕω+=t A t x 的概率密度函数p(x)。

信号分析的基本方法

信号分析的基本方法

2021/4/15
12
图2.2 余弦信号的频谱
A A0
0
0
(a) 幅度谱
2021/4/15
0
0
0
(b) 相位谱
13
• 图2.2在新的坐标系（角频率或频率为横 轴，，振幅和相位为纵轴）中，以两条 线（甚至两个点就够了），表示了时域 波形如图2.1所示的信号，或者说，表示 了信号所有的特征信息（频率、幅度和 相位）。这种表示法被称为频域表示， 表示的结果叫做“频谱”，对应于振幅 或者相位分别为幅度谱和相位谱。
22
图2.4 各种信号
f t
f nT
5
3
0
t
(a) 模拟信号
f t
5
1
0
nT
(b) 抽样信号
f n
5
3
3
1
t
1
0
t
0
n
(c) 量化信号
(d) 数字信号
2021/4/15
23
按信号的时间或频率定义范围
• 在有限的时间区间内有定义，而在区间 外为零，这类信号叫做时域有限信号， 简称时限信号。矩形脉冲、正弦脉冲等 信号都属这种类型。而周期信号、指数 信号、随机信号等，则属于时域无限信 号。
（ Fn ,
n 0）都降为对应实幅谱（
C
）
n
的一半；后者呈奇对称，复谱与实谱的
相位谱值相等。
• 复指数形式的傅里叶级数（对应于复频 谱）是周期信号频域分析的最基本方法。
2021/4/15
38
【例2-1】
• 【例2-1】 试求图2.6所示的周期矩形脉 冲信号的频谱。
f t
E
...

工程测试技术 信号分析基础

工程测试技术 信号分析基础

t1 2
24
yzs (t)
⑤ 3≤t 时
2 1 d 1 t2 1 t 3
t1 2
4 24
29 f ( t -τ) h(τ) = 0，故 yzs(t) = 0
0
t-1 t t-1 t t-1 t 2
τt
h(τ )f (t -τ )
0 t t-1 1t t-1 2 3 τ yf (t )
-T0
T0
h(T0/2- )
-T0
T0
A2
-T0
T0
2.6 卷积分
y(t) x( )h(t )d x(t) h(t) y(t)
2A2T0
-2T0
t= T0时：
0
2T0
y(T0)=A2 T0
10
x()
-T0
T0
h(T0- )
-T0
T0
A2
-T0
T0
2.6 卷积分
y(t) x( )h(t )d x(t) h(t) y(t)
x(t)
(1)换元
h(t)
反折；
0
t (2)平移；
0
t
x(t)
(4)积分
(3)相乘； h(-)
(1)反折
(4)积分。
0
x(t)
h(t1 -)
t (3)相乘
0
h(t1 -)
(2)平移
00
t
23
0
2.6 卷积分
图解法一般比较繁琐，确定积分的上下限是关键。
e(t)或e( )
h(t)或h( )
• 举例 1
t (6 e2te3 e ) d
e2t t (6 e3 ) d t e d
e2t 2 e3

信号的时域波形分析

信号的时域波形分析
以幅值大小为横坐标，以每个幅值间隔内出现 的概率为纵坐标进行统计分析的方法。它反映了信 号落在不同幅值强度区域内的概率情况。
p (x)limp (x x( t) x x x) x
随△x的变化，是幅值x的函数
第二章、信号分析基础
河南科技大学
p(x)的计算方法：
p(x) lim1 x[ limT T x] x 0 T
河南科技大学
x ( t) c 1 x 1 ( t) c 2 x 2 ( t) ...... c n x n ( t)
正交函数集（三角函数、复指数函数、沃尔什函数等）
第二章、信号分析基础 d.偶分量和奇分量
河南科技大学
x(t)xe(t)xo(t)
第二章、信号分析基础
河南科技大学
e.实部分量和虚部分量
河南科技大学
2.2 信号的时域波形分析
河南科技大学
第二章、信号分析基础
2.3 信号的幅值域分析
河南科技大学
幅值域分析：在时域中，采用统计分析的方法，描述幅值 取值大小及其频率（概率密度函数、概率分布函数、联合 概率密度函数）
第二章、信号分析基础
2.3 信号的幅值域分析
河南科技大学
1 概率密度函数
（4）随机噪声信号的自相关函数将随 的增大快 速衰减。
2.4 信号的时差域相关分析
河南科技大学
（5）两周期信号的互相关函数仍然是同频率的周 期信号，且保留原了信号的相位信息。
（6）两个非同频率的周期信号互不相关。
2.4 信号的时差域相关分析
相关分析的工程应用
案例：机械加工表面粗糙度自相关分析
如果所研究的变量x, y是与时间有关的函数， 即x(t)与y(t)：

1.2信号分析基础(时域波形分析、相关分析、随机信号)

1.2信号分析基础(时域波形分析、相关分析、随机信号)

浙江工业大学
∫
T
0
(x(t ) − µ x )2 dt
大方差
小方差
方差：反映了信号绕均值的波动程度。 方差：反映了信号绕均值的波动程度。
第二章、 第二章、信号分析基础
浙江工业大学
2.4 信号的幅值域分析
1 概率密度函数 以幅值大小为横坐标，以每个幅值间隔内出现 以幅值大小为横坐标， 的概率为纵坐标进行统计分析的方法。 的概率为纵坐标进行统计分析的方法。它反映了信 号落在不同幅值强度区域内的概率情况。 号落在不同幅值强度区域内的概率情况。
2.5 信号的时差域相关分析
浙江工业大学
（5）两周期信号的互相关函数仍然是同频率的周 期信号，且保留原了信号的相位信息。 期信号，且保留原了信号的相位信息。 （6）两个非同频率的周期信号互不相关。 两个非同频率的周期信号互不相关。
2.5 信号的时差域相关分析
浙江工业大学
2.5 信号的时差域相关分析
µ x = E [ x (t )] = lim
T 1 T 0 T → ∞
∫
x (t ) dt
µx
Байду номын сангаас
均值：反映了信号变化的中心趋势， 均值：反映了信号变化的中心趋势，也称之 为直流分量。 为直流分量。
2.3 信号的时域波形分析
浙江工业大学
5、均方值 信号的均方值E[x2(t)]，表达了信号的强度； 信号的均方值E[x (t)]，表达了信号的强度； 其正平方根值，又称为有效值(RMS) (RMS)， 其正平方根值，又称为有效值(RMS)，也是信号 平均能量的一种表达。 平均能量的一种表达。
浙江工业大学
相关分析的工程应用
案例：机械加工表面粗糙度自相关分析 案例：
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
50Hz正弦波信号波形
第二章信号分析基础
机械系统中，回转体不平衡引起的振动，往往也是一种周期性运动。 例如，下图是某钢厂减速机上测得的振动信号波形(测点3)，可以近似的 看作为周期信号:
某钢厂减速机振动测点布置图
第二章信号分析基础
测点３振动信号波形
第二信号分析基础
非周期信号是不会重复出现的信号。例如，锤子的敲击力；承载缆 绳断裂时应力变化；热电偶插入加热炉中温度的变化过程等，这些信号 都属于瞬变非周期信号，并且可用数学关系式描述。例如，下图是单自 由度振动模型在脉冲力作用下的响应。
单自由度振动模型脉冲响应信号波形
第二章信号分析基础
准周期信号是周期与非周期的边缘情况，是由有限个周期信号合成 的，但各周期信号的频率相互间不是公倍关系，其合成信号不满足周期 条件，例如 是两个正弦信号的合成，其频率比不是有理数，不成谐波关 系。下面是其信号波形：
准周期信号sin(t)+sin(1.41t)波形
信号的分类描述
第二章信号分析基础
周期信号是经过一定时间可以重复出现的信号，满足条件： x ( t ) = x ( t + nT )
式中，T——周期，T=2π/ω0；ω0——基频；n=0,±1, …。 例如，下面是一个50Hz正弦波信号10sin(2*3.14*50*t)的波形，信号
周期为：1/50=0.02秒:
第二章信号分析基础
离散时间信号
2.1.5 物理可实现信号
物理可实现信号又称为单边信号，满足条件：t＜0时，x(t) = 0， 即在时刻小于零的一侧全为零，信号完全由时刻大于零的一侧确定。
第二章信号分析基础
在实际中出现的信号，大量的是物理可实现信号，因为这种信号反 映了物理上的因果律．实际中所能测得的信号，许多都是由一个激发脉 冲作用于一个物理系统之后所输出的信号．例如，切削过程，可以把机 床、刀具、工件构成的工艺系统作为一个物理系统，把工件上的硬质点 或切削刀具上积屑瘤的突变等，作为振源脉冲，仅仅在该脉冲作用于系 统之后，振动传感器才有描述刀具振动的输出。
在区间（t1，t2）内，信号的平均功率
第二章信号分析基础
若区间变为无穷大时，上式仍然大于零，那么信号具有有限的平均 功率，称之为功率信号．具体讲，功率信号满足条件：
对比上式，显而易见，一个能量信号具有零平均功率，而一个功率 信号具有无限大能量．
2.1.3.时限与频限信号
时域有限信号是在有限区间（t1，t2 ）内定义，而其外恒等于 零．例如，矩形脉冲、三角脉冲、余弦脉冲等。而周期信号、指数衰 减信号、随机过程等，则称为时城无限信号 。
加工过程中螺纹车床主轴受环境影响的振动信号波形
然而，须要指出的是，实际物理过程往往是很复杂的，既无 理想的确定性，也无理想的非确定性，而是相互参杂的。
第二章信号分析基础
2.1.2 能量信号与功率信号 a)能量信号
在所分析的区间（-∞，∞），能量为有限值的信号称为能量信号， 满足条件：
关于信号的能量，可作如下解释：对于电信号，通常是电压或电流， 电压在已知区间（t1；，t2 ）内消耗在电阻上的能量
第二章信号分析基础
2.1.4.连续时间信号与离散时间信号
连续时间信号：在所讨论的时间间隔内，对于任意时间值(除若干个 第一类间断点外)都可给出确定的函数值，此类信号称为连续时间信号或 模拟信号。连续信号的幅值可以是连续的也可以是不连续的。
离散时间信号：离散时间信号在时间上是离散的．只是在某些不连 续的规定瞬时给出函数值，而在其他时间没有定义的信号。
对于电流，能量
第二章信号分析基础
在上面每一种情况下，能量都是正比于信号平方的积分．讨论消耗 在IQ电阻上的能量往往是很方便的，因为当R—IQ时，上述两式具有相 同形式，采用这种规定时，就称方程
为任意信号x(t)的“能量”。
b)功率信号
有许多信号，如周期信号、随机信号等，它们在区间（-∞，∞） 内能量不是有限值．在这种情况下，研究信号的平均功率更为合适．
这种信号往往出现于通信、振动系统，应用于机械转子振动分析， 齿轮噪声分析，语音分析等场合。
第二章信号分析基础
b)非确定性信号 非确定性信号不能用数学关系式描述，其幅值、相位变化是不可
预知的，所描述的物理现象是一种随机过程。例如，汽车奔驰时所产 生的振动；飞机在大气流中的浮动；树叶随风飘荡；环境噪声等。
第二章 信号分析基础
本章学习要求
完成本章内容的学习后应能作到： 1.了解信号分类方法 2.掌握信号波形分析方法 3.掌握信号相关分析方法 4.掌握信号频谱分析方法 5.了解其它信号分析方法
第二章信号分析基础
2.1 信号的分类与描述
为了深入了解信号的物理实质，将其进行分类研究是非常必 要的。以不同的角度来看待信号，我们可以将信号分为
物理可实现信号
第二章信号分析基础
所谓物理系统，具有这样一种性质，当激发脉冲作用于系统之前， 系统是不会有响应的，换句话说，在零时刻之前，没有输入脉冲，则输 出为零，这种性质反映了物理上的因果关系．因此，一个信号要通过一 个物理系统来实现，就必须满足x（t）= 0（t＜O＝，这就是把满足这一 条件的信号称之为物理可实现信号的原因．同理，对于离散信号而言， 满足x（n）= 0（n＜0＝条件的序列，即称为因果序列。
1. 确定性信号与非确定性信号 2. 能量信号与功率信号 3. 时限信号与频限信号 4. 连续时间信号与离散时间信号 5. 物理可实现信号
第二章信号分析基础
2.1.1 确定性信号与非确定性信号
a)确定性信号 可以用明确的数学关系式描述的信号称为确定性信号。它可以进
一步分为周期信号、非周期信号与准周期信号等，如下图所示。
时域有限信号
第二章信号分析基础
频域有限信号是指信号经过傅里叶变换，在频域内占据一定带宽 （f1 ，f2），其外恒等于零．例如，正弦信号、sinc（t）函数、限带 白噪声等，为时城无限频域有限信号。白噪声、理想采样信号等，则 为频域无限信号．
频域有限信号
时间有限信号的频谱，在频率轴上可以延伸至无限远。由时、频域 对称性可推论，一个具有有限带宽的信号，必然在时间轴上延伸至无限 远处。显然，一个信号不能够在时域和频域都是有限的。