平面三角形单元有限元程序设计
- 格式:doc
- 大小:255.79 KB
- 文档页数:9


平面三角形单元有限元程序设计P9 m 9 m一、题目如图1所示,一个厚度均匀的三角形薄板,在顶点作用沿板厚方向均匀分布的竖向载荷。
已知:P=150N/m,E=200GPa,=0、25,t=0、1m,忽略自重。
试计算薄板的位移及应力分布。
要求:1.编写有限元计算机程序,计算节点位移及单元应力。
(划分三角形单元,单元数不得少于30个);2.采用有限元软件分析该问题(有限元软件网格与程序设计网格必须一致),详细给出有限元软件每一步的操作过程,并将结果与程序计算结果进行对比(任选取三个点,对比位移值);3.提交程序编写过程的详细报告及计算机程序;4.所有同学参加答辩,并演示有限元计算程序。
有限元法中三节点三角形分析结构的步骤如下:1)整理原始数据,如材料性质、荷载条件、约束条件等,离散结构并进行单元编码、结点编码、结点位移编码、选取坐标系。
2)单元分析,建立单元刚度矩阵。
3)整体分析,建立总刚矩阵。
4)建立整体结构的等效节点荷载与总荷载矩阵5)边界条件处理。
6)解方程,求出节点位移。
7)求出各单元的单元应力。
8)计算结果整理。
一、程序设计网格划分如图,将薄板如图划分为6行,并建立坐标系,则刚度矩阵的集成建立与总刚度矩阵等维数的空矩阵,已变单元刚度矩阵的集成。
由单元分析已知节点、单元的排布规律,继而通过循环计算求得每个单元对应的节点序号。
通过循环逐个计算:(1)每个单元对应2种单元刚度矩阵中的哪一种; (2)该单元对应总刚度矩阵的那几行哪几列 (3)将该单元的单元刚度矩阵加入总刚度矩阵的对应行列循环又分为3层循环:(1)最外层:逐行计算(2)中间层:该行逐个计算(3)最里层:区分为第 奇/偶 数个计算XYPXYP节点编号单元编号单元刚度的集成:[][][][][][]''''''215656665656266256561661eZeeeZeZeeeekkkKkkkkkk+⋯++=⇓=⇒==⇒==⇒=⨯⨯⨯⨯⨯⨯M边界约束的处理:划0置1法适用:这种方法适用于边界节点位移分量为已知(含为0)的各种约束。

matlab有限元三角形单元编程
在MATLAB中进行有限元分析,可以使用其自带的有限元分析工具箱(FEATool)进行编程。
以下是一个简单的例子,演示如何使用三角形单元进行有限元分析:
1. 打开MATLAB,进入FEATool环境。
2. 创建新的有限元模型。
选择“Model”菜单下的“New Model”选项,进入“Model Builder”界面。
3. 在“Model Builder”界面中,选择“2D Triangle”单元类型,并在绘图区域中绘制出三角形网格。
4. 在“Model Builder”界面中,设置材料属性、边界条件和载荷等参数。
5. 运行有限元分析。
选择“Model”菜单下的“Solve”选项,进行有限元求解。
6. 查看结果。
选择“Model”菜单下的“Results”选项,可以查看位移、应力、应变等结果。
以上是一个简单的例子,演示了如何使用三角形单元进行有限元分析。
在实际应用中,还需要根据具体问题进行详细的建模和计算。

第2章弹性力学平面问题有限单元法2.1 三角形单元(triangular Element)三角形单元是有限元分析中的常见单元形式之一,它的优点是:①对边界形状的适应性较好,②单刚形式及其推导比较简单,故首先介绍之。
一、结点位移和结点力列阵设右图为从某一结构中取出的一典型三角形单元。
在平面应力问题中,单元的每个结点上有沿x、y两个方向的力和位移,单元的结点位移列阵规定为:相应结点力列阵为: (式2-1-1)二、单元位移函数和形状函数前已述及,有限单元法是一种近似方法,在单元分析中,首先要求假定(构造)一组在单元内有定义的位移函数作为近似计算的基础。
即以结点位移为已知量,假定一个能表示单元内部(包括边界)任意点位移变化规律的函数。
构造位移函数的方法是:以结点(i,j,m)为定点。
以位移(u i ,v i ,…u m v m )为定点上的函数值,利用普通的函数插值法构造出一个单元位移函数。
在平面应力问题中,有u,v两个方向的位移,若假定单元位移函数是线性的,则可表示成:(,)123u u x y x yααα==++546(,)v v x y x yααα==++(2-1-2)a式中的6个待定常数α1 ,…, α6 可由已知的6个结点位移分量(3个结点的坐标) {}⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=mjimeddddmjjivuvuvui{}iijjmXYX(2-1-1)YXYiejmmFF FF⎧⎫⎪⎪⎪⎪⎧⎫⎪⎪⎪⎪⎪⎪==⎨⎬⎨⎬⎪⎪⎪⎪⎩⎭⎪⎪⎪⎪⎪⎪⎩⎭确定。
将3个结点坐标(x i,y i ),(x j,y j ),(x m,y m )代入上式得如下两组线性方程:123i i i u x y ααα=++ 123j j j u x y ααα=++ (a)123m m m u x y ααα=++和546i i i v x y ααα=++ 546j j j v x y ααα=++ (b)546m m m v x y ααα=++利用线性代数中解方程组的克来姆法则,由(a)可解出待定常数1α 、2α 、3α :11A Aα=22A Aα=33A Aα=式中行列式:1i i i j j j m m m u x y A u x y u x y =2111i i j j m mu y A u y u y =3111i i j j m m x u A x u x u = 2111i i j j m mAx y A x y x y ==A 为△ijm 的面积,只要A 不为0,则可由上式解出:11()2m m i ij j a u a u a u A α=++ 21()2m m i ij j bu b u b u A α=++ (C )31()2m mi i j j c u c u c u A α=++式中:m m i j j a x y x y =- m m j i i a x y x y =- m i j j i a x y x y =-m i j b y y =- m j i b y y =- m i j b y y =- (d )m i j c x x =- m j i c x x =- m j i c x x =-为了书写方便,可将上式记为: m m i j ia x y x y =-m ij by y =- (,,)i j m u u u u ruu u u r m i jc x x =-(,,)i j m u u u u ru u u u r表示按顺序调换下标,即代表采用i,j,m 作轮换的方式便可得到(d)式。


平面三角形3结点有限元程序1、程序名:,2、程序功能本程序能计算弹性力学的平面应力问题和平面应变问题;能考虑自重和结点集中力两种荷载的作用,在计算自重时y轴取垂直向上为正;能处理非零已知位移,如支座沉降的作用。
主要输出的内容包括:结点位移、单元应力、主应力、第一主应力与x轴的夹角以及约束结点的支座反力。
程序采用Visual Fortran 编制而成,输入数据全部采用自由格式。
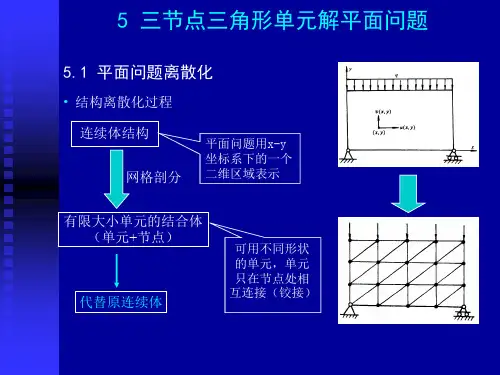
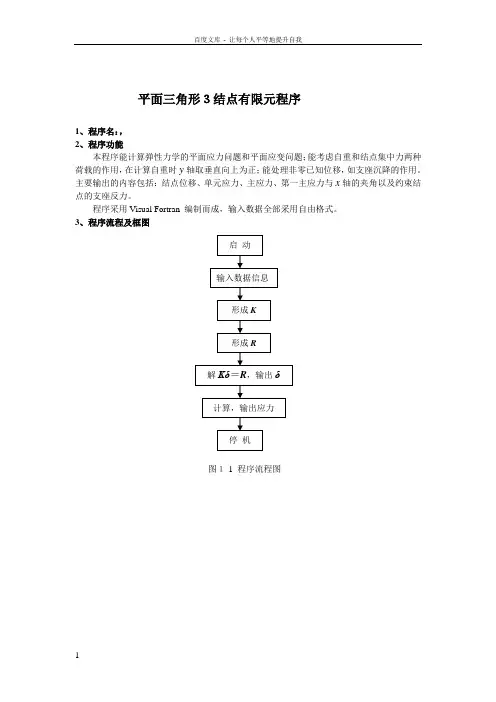
3、程序流程及框图图1-1 程序流程图图1-2 程序框图其中,各子程序的功能如下:INPUT——输入结点坐标、单元信息和材料参数;MR——形成结点自由度序号矩阵;FORMMA——形成指标矩阵MA(N)并调用其他功能子程序,相当于主控程序;DIV——取出单元的3个结点号码和该单元的材料号并计算单元的b i,c i等;MGK——形成整体劲度矩阵并按一维存放在SK(NH)中;LOAD——形成整体结点荷载列阵F;OUTPUT——输出结点位移或结点荷载;TREAT——由于有非零已知位移,对K和F进行处理;DECOMP——整体劲度矩阵的分解运算;FOBA——前代、回代求出未知结点位移δ;ERFAC——计算约束结点的支座反力;KRS——计算单元劲度矩阵中的子块K rs。
4、输入数据及变量说明当程序开始运行时,按屏幕提示,键入数据文件的名字。
在运行程序之前,必须根据程序中输入要求建立一个存放原始数据的文件,这个文件的名字由少于8个字符或数字组成。
数据文件包括如下内容:⑴总控信息,共一条,9个数据NP,NE,NM,NR,NI,NL,NG,ND,NCNP——结点总数;NE——单元总数;NM——材料类型总数;NR——约束结点总数;NI ——问题类型标识,0为平面应力问题,1为平面应变问题;NL ——受荷载作用的结点的数目;NG ——考虑自重作用为1,不计自重为0;ND ——非零已知位移结点的数目;NC ——要计算支座约束反力的结点数目。
⑵ 材料信息,共NM 条,每条依次输入EO ,VO ,W ,tEO ——弹性模量(kN/m 2);VO ——泊松比;W ——材料容重(kN/m 3);t ——单元厚度(m )。


第二章 弹性力学平面问题有限单元法§2-1 三角形单元(triangular Element)三角形单元是有限元分析中的常见单元形式之一,它的优点是:①对边界形状的适应性较好,②单刚形式及其推导比较简单,故首先介绍之。
一、结点位移和结点力列阵设右图为从某一结构中取出的一典型三角形单元。
在平面应力问题中,单元的每个结点上有沿x 、y 两个方向的力和位移,单元的结点位移列阵规定为: 相应结点力列阵为: (式2-1-1)二、单元位移函数和形状函数前已述及,有限单元法是一种近似方法,在单元分析中,首先要求假定(构造)一组在单元内有定义的位移函数作为近似计算的基础。
即以结点位移为已知量,假定一个能表示单元内部(包括边界)任意点位移变化规律的函数。
构造位移函数的方法是:以结点(i,j,m)为定点。
以位移(u i ,v i ,…u m v m )为定点上的函数值,利用普通的函数插值法构造出一个单元位移函数。
在平面应力问题中,有u,v 两个方向的位移,若假定单元位移函数是线性的,则可表示成:(,)123u u x y x y ααα==++546(,)v v x y x y ααα==++ (2-1-2)a{}⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=m j i m ed d d d m j j i v u v u v u i {}ii j j m X Y X (2-1-1)Y X Y iej m m F F F F ⎧⎫⎪⎪⎪⎪⎧⎫⎪⎪⎪⎪⎪⎪==⎨⎬⎨⎬⎪⎪⎪⎪⎩⎭⎪⎪⎪⎪⎪⎪⎩⎭式中的6个待定常数α1 ,…, α6 可由已知的6个结点位移分量(3个结点的坐标)确定。
将3个结点坐标(x i,y i ),(x j,y j ),(x m,y m )代入上式得如下两组线性方程:123i i i u x y ααα=++123j j j u x y ααα=++ (a)123m m m u x y ααα=++和546i i i v x y ααα=++546j j j v x y ααα=++ (b)546m m m v x y ααα=++利用线性代数中解方程组的克来姆法则,由(a)可解出待定常数1α 、2α 、3α :11A Aα=22A Aα=33A Aα=式中行列式:1i i i j j j m m m u x y A u x y u x y =2111i i j j m mu y A u y u y =3111i i j jm mx u A x u x u =2111i i j j m mAx y A x y x y ==A 为△ijm 的面积,只要A 不为0,则可由上式解出:11()2m m i ij j a u a u a u A α=++ 21()2m m i ij j bu b u b u A α=++ (C )31()2m mi i j j c u c u c u A α=++式中:m m i j j a x y x y =- m m j i i a x y x y =- m i j j i a x y x y =-m i j b y y =- m j i b y y =- m i j b y y =- (d )m i j c x x =- m j i c x x =- m j i c x x =-为了书写方便,可将上式记为:m m i j i a x y x y =-m ij by y =- (,,)i j mm i jc x x =-(,,)i j m表示按顺序调换下标,即代表采用i,j,m 作轮换的方式便可得到(d)式。

实验三:三角形单元的形函数性质验证
一、 实验目的
1、加深对平面三角形单元有限元分析过程的理解;
2、掌握平面三角形单元形函数矩阵的求解过程和性质。
二、 实验要求
1、明确形函数矩阵的含义和求法;
2、根据题目要求,给出具体的计算过程;
3、编制相应的matlab 计算程序并调试运行。
三、 实验内容
用有限元法求图示平面三角形单元的形函数。
已知节点i,j,m 在xoy 平面中的坐标分别为(5,2),(3,4),(1,1)。
用所编程序验证形函数特性:
1、在单元任一点上,三个形函数之和等于1;
2、形函数N i 在i 点的函数值为1,在j 点及m 点的函数值为零;
3、三边上任一点的形函数与第三个顶点的坐标无关。
四、 实验提示
1、()() 21,y c x b a y x N i i i i ++∆=
,其中下标i , j , m 轮换; 2、()()m i j m i j i m m j j i y x y x y x y x y x y x ++++=∆2
1 -21; 3、j m i m m i j m m j i x x c y y b y x y x a -=-=-=;;,其中下标i , j , m 轮换。
第15卷第2期 2007年4月安徽建筑工业学院学报(自然科学版)Journal of Anhui Institute of Architecture &IndustryVol.15No.2 Apr.2007 收稿日期:2006201223作者简介:凡大林(1981-)男,硕士研究生,主要研究方向为工程结构分析与计算机辅助设计、仿真。
利用Maple 编制平面问题有限元程序凡大林, 方诗圣(合肥工业大学土木建筑工程学院,合肥 230009)摘 要:文章通过分别使用Maple 与Fortran 语言编程解决同一问题的比较,使读者可以容易地了解到Maple 软件比其他计算机语言进行编程时,更简洁、直观,而且降低了对编程者的数学要求,并且结合具体算例进一步介绍了如何应用Maple 的这些优点,编制有限元程序,解决工程中常遇到的平面问题。
为应用Maple 软件编制有限元计算程序提供一种可借鉴的模式。
关键词:Maple ;平面问题;有限元程序中图分类号:TP311.1 文献标识码:A 文章编号:100624540(2007)022081204Application of maple to make f inite element programFAN Da 2lin , FAN G Shi 2sheng(School of Civil Engineering ,Hefei University of Technology ,Hefei 230009,China )Abstract :This paper make t he reader known maple ’s advantages such as int uitive exp ression form ,lit 2tle mat he t heory demand Easily by solving t he same p roblem in Maple and Fort ran.The paper int ro 2duces how to use t hese advantages to make Finite Elment Program to solve plannar problem This st udy p rovides a good reference mode for making Finite Elment Program in Maple.K ey w ords :Maple ;plane problem ;Finite Element Program Maple 软件是由加拿大沃特卢(Waterloo )大学研发的一个具有强大符号运算能力、数值运算能力、图形处理能力的交互式计算机代数系统[1]。
平面三角形3结点有限元程序1、程序名:FEM3.FOR,FEM3.EXE2、程序功能本程序能计算弹性力学的平面应力问题和平面应变问题;能考虑自重和结点集中力两种荷载的作用,在计算自重时y轴取垂直向上为正;能处理非零已知位移,如支座沉降的作用。
主要输出的内容包括:结点位移、单元应力、主应力、第一主应力与x轴的夹角以及约束结点的支座反力。
程序采用Visual Fortran 5.0编制而成,输入数据全部采用自由格式。
3、程序流程及框图图1-1 程序流程图图1-2 程序框图其中,各子程序的功能如下:INPUT——输入结点坐标、单元信息和材料参数;MR——形成结点自由度序号矩阵;FORMMA——形成指标矩阵MA(N)并调用其他功能子程序,相当于主控程序;DIV——取出单元的3个结点号码和该单元的材料号并计算单元的bi ,ci等;MGK——形成整体劲度矩阵并按一维存放在SK(NH)中;LOAD——形成整体结点荷载列阵F;OUTPUT——输出结点位移或结点荷载;TREA T——由于有非零已知位移,对K和F进行处理;DECOMP——整体劲度矩阵的分解运算;FOBA——前代、回代求出未知结点位移 ;ERFAC——计算约束结点的支座反力;KRS——计算单元劲度矩阵中的子块K rs。
4、输入数据及变量说明当程序开始运行时,按屏幕提示,键入数据文件的名字。
在运行程序之前,必须根据程序中输入要求建立一个存放原始数据的文件,这个文件的名字由少于8个字符或数字组成。
数据文件包括如下内容:⑴总控信息,共一条,9个数据NP,NE,NM,NR,NI,NL,NG,ND,NCNP——结点总数;NE——单元总数;NM——材料类型总数;NR ——约束结点总数;NI ——问题类型标识,0为平面应力问题,1为平面应变问题; NL ——受荷载作用的结点的数目;NG ——考虑自重作用为1,不计自重为0; ND ——非零已知位移结点的数目; NC ——要计算支座约束反力的结点数目。
. 一、题目如图1所示,一个厚度均匀的三角形薄板,在顶点作用沿板厚方向均匀分布的竖向载荷。
已知:P=150N/m ,E=200GPa ,=0.25,t=0.1m ,忽略自重。
试计算薄板的位移及应力分布。
要求: 1. 编写有限元计算机程序,计算节点位移及单元应力。
(划分三角形单元,单元数不得少于30个);2. 采用有限元软件分析该问题(有限元软件网格与程序设计网格必须一致),详细给出有限元软件每一步的操作过程,并将结果与程序计算结果进行对比(任选取三个点,对比位移值);3. 提交程序编写过程的详细报告及计算机程序;4. 所有同学参加答辩,并演示有限元计算程序。
有限元法中三节点三角形分析结构的步骤如下:1)整理原始数据,如材料性质、荷载条件、约束条件等,离散结构并进行单元编码、结点编码、结点位移编码、选取坐标系。
2)单元分析,建立单元刚度矩阵。
3)整体分析,建立总刚矩阵。
4)建立整体结构的等效节点荷载和总荷载矩阵5)边界条件处理。
6)解方程,求出节点位移。
7)求出各单元的单元应力。
8)计算结果整理。
一、程序设计网格划分如图,将薄板如图划分为6行,并建立坐标系,则刚度矩阵的集成建立与总刚度矩阵等维数的空矩阵,已变单元刚度矩阵的集成。
由单元分析已知节点、单元的排布规律,继而通过循环计算求得每个单元对应的节点序号。
通过循环逐个计算:(1)每个单元对应2种单元刚度矩阵中的哪一种;(2)该单元对应总刚度矩阵的那几行哪几列(3)将该单元的单元刚度矩阵加入总刚度矩阵的对应行列循环又分为3层循环:(1)最外层:逐行计算(2)中间层:该行逐个计算(3)最里层:区分为第 奇/偶 数个计算单元刚度的集成:[][][][][][]''''''215656665656266256561661e Z e e e Z e Z e e e e k k k K k k k k k k +⋯++=⇓=⇒==⇒==⇒=⨯⨯⨯⨯⨯⨯边界约束的处理:划0置1法X Y P X Y P适用:这种方法适用于边界节点位移分量为已知(含为0)的各种约束。
做法:(1)将总刚矩阵〔K〕中相应于已知位移行主对角线元素置1,其他元素改为零;同时将载荷列阵{R}中相应元素用已知位移置换。
◎这样,由该方程求得的此位移值一定等于已知量。
(2)将〔K〕中已知位移相应的列的非主对角成元素也置0,以保持〔K〕的对称性。
◎当然,在已知位移分量不为零的情况下,这样做就改变了方程左端的数值,为保证方程成立,须在方程右端减去已知位移对该方程的贡献——已知位移和相应总刚元素的乘积。
◎若约束为零位移约束时,此步则可省去。
特点:(1)经以上处理同样可以消除刚性位移(约束足够的前提下),去掉未知约束反力。
(2)但这种方法不改变方程阶数,利于存贮。
(3)不过,若是要求出约束反力,仍要重新计算各个划去的总刚元素。
程序如下:变量说明NNODE 单元节点数NPION 总结点数NELEM 单元数NVFIX 受约束边界点数FIXED 约束信息数组NFORCE 节点力数FORCE 节点力数组COORD 结构节点坐标数组LNODS 单元定义数组YOUNG 弹性模量POISS 泊松比THICK 厚度B 单元应变矩阵(3*6)D 单元弹性矩阵(3*3)S 单元应力矩阵(3*6)A 单元面积ESTIF 单元刚度矩阵ASTIF 总体刚度矩阵ASLOD 总体荷载向量ASDISP 节点位移向量ELEDISP 单元节点位移向量STRESS 单元应力%********************************************************** %初始化clearformat short e %设定输出类型clear %清除内存变量NELEM=36 %单元个数(单元编码总数)NPION=28 %结点个数(结点编码总数)NVFIX=2 %受约束边界点数NFORCE=1 %结点荷载个数YOUNG=2e11 %弹性模量POISS=0.25 %泊松比THICK=0.1 %厚度LNODS=[1 2 3;2 4 5;2 5 3;3 5 6;4 7 8;4 8 5;5 8 9;5 9 6;6 9 10;7 11 12;7 12 8;8 12 13;8 13 9;9 13 14;9 14 10;10 14 15;11 16 17;11 17 12; 12 17 18; 12 18 13;13 18 19; 13 19 14;14 19 20;14 20 15;15 20 21;16 22 23;16 23 17;17 23 24;17 24 18;18 24 25;18 25 19;25 19 26;19 26 20;20 26 27;20 27 21;21 27 28] %单元定义数组(单元结点号)%相应为单元结点号(编码)、按逆时针顺序输入COORD=[0 0;-0.75 1.5;0.75 1.5;-1.5 3;0 3;1.5 3;-2.25 4.5;-0.75 4.5;0.75 4.5;2.25 4.5;-3 6;-1.5 6;0 6;1.5 6;3 6;-3.75 7.5;-2.25 7.5; -0.75 7.5;0.75 7.5;2.25 7.5;3.75 7.5;-4.5 9;-3 9;-1.5 9;0 9;1.5 9;3 9;4.5 9] %结点坐标数组%坐标:x,y 坐标(共NPOIN 组)FORCE=[1 0 -15] %结点力数组(受力结点编号, x 方向,y 方向)FIXED=[22 1 1;28 1 1] %约束信息(约束点,x 约束,y 约束)%有约束为1,无约束为0%********************************************************** %生成单元刚度矩阵并组成总体刚度矩阵ASTIF=zeros(2*NPION,2*NPION); %生成特定大小总体刚度矩阵并置0%********************************************************** for i=1:NELEM%生成弹性矩阵 DD= [1 POISS 0;POISS 1 0;0 0 (1-POISS)/2]*YOUNG/(1-POISS^2)%********************************************************** %计算当前单元的面积A=-det([1 COORD(LNODS(i,1),1) COORD(LNODS(i,1),2);1 COORD(LNODS(i,2),1) COORD(LNODS(i,2),2);1 COORD(LNODS(i,3),1) COORD(LNODS(i,3),2)])/2%********************************************************** %生成应变矩阵 Bfor j=0:2b(j+1)=COORD(LNODS(i,(rem((j+1),3))+1),2)-COORD(LNODS(i,(re m((j+2),3))+1),2);c(j+1)=-COORD(LNODS(i,(rem((j+1),3))+1),1)+COORD(LNODS(i,(r em((j+2),3))+1),1);endB=[b(1) 0 b(2) 0 b(3) 0;0 c(1) 0 c(2) 0 c(3);c(1) b(1) c(2) b(2) c(3) b(3)]/(2*A);B1( :,:,i)=B;%********************************************************** %求应力矩阵S=D*BS=D*B;ESTIF=B'*S*THICK*A; %求解单元刚度矩阵a=LNODS(i,:); %临时向量,用来记录当前单元的节点编号for j=1:3for k=1:3ASTIF((a(j)*2-1):a(j)*2,(a(k)*2-1):a(k)*2)=ASTIF((a(j)*2-1) :a(j)*2,(a(k)*2-1):a(k)*2)+ESTIF(j*2-1:j*2,k*2-1:k*2);%根据节点编号对应关系将单元刚度分块叠加到总刚%度矩阵中endendend%********************************************************** %将约束信息加入总体刚度矩阵(对角元素改一法)for i=1:NVFIXif FIXED(i,2)==1ASTIF(:,(FIXED(i,1)*2-1))=0; %一列为零ASTIF((FIXED(i,1)*2-1),:)=0; %一行为零ASTIF((FIXED(i,1)*2-1),(FIXED(i,1)*2-1))=1; %对角元素为 1end%********************************************************** %生成单元刚度矩阵并组成总体刚度矩阵%**********************************************************if FIXED(i,3)==1ASTIF( :,FIXED(i,1)*2)=0; %一列为零ASTIF(FIXED(i,1)*2,:)=0; %一行为零ASTIF(FIXED(i,1)*2 ,FIXED(i,1)*2)=1; %对角元素为 1endend%********************************************************** %生成荷载向量ASLOD(1:2*NPION)=0; %总体荷载向量置零for i=1:NFORCEASLOD((FORCE(i,1)*2-1):FORCE(i,1)*2)=FORCE(i,2:3);end%********************************************************** %求解内力ASDISP=ASTIF\ASLOD' %计算节点位移向量ELEDISP(1:6)=0; %当前单元节点位移向量for i=1:NELEMfor j=1:3ELEDISP(j*2-1:j*2)=ASDISP(LNODS(i,j)*2-1:LNODS(i,j)*2);%取出当前单元的节点位移向量endiSTRESS=D*B1(:, :, i)*ELEDISP' %求内力end(程序计算结果和有限元软件得出的结果稍有偏差,可能是程序某些地方数据输入时出了问题,还在寻找具体原因)二、有限元软件分析设置材料参数建模网格划分。